基于变尺度滤波的含分布式风电直流线路监测
徐 彦 夏经德 罗金玉 邵文权 苗思雨杨秀川
(1.西安工程大学电子信息学院,陕西省 西安市 710048;2.西安交通大学电气工程学院,陕西省 西安市 710049;3.大唐陕西发电有限公司,陕西省 西安市 710061)
0 引言
在我国“碳达峰,碳中和”战略目标下,分布式清洁能源在能源结构中的占比日益增加[1-2]。自2014年以来,风力发电迅速成为新能源发电的主流之一,我国分布式风电装机容量逐年提升,现装机总容量已超93.5×104kW[3]。相较于交流电网,直流电网具有消纳新能源能力强、输电效率高、减少换流环节等优点[4],直流电网更契合分布式风力发电的发展,但并网也面临着诸多问题亟待解决。当风力发电接入直流电网需换流器的加入,换流器中诸多电力电子器件频繁开关断使系统电气量中含有大量谐波,对系统状态监测和继电保护的判别产生影响[5]。换流器中的电力电子器件具有天然的脆弱性,对系统状态监测和继电保护的快速判别提出了更高的要求[6]。
为提高含分布式风电的直流输电系统的安全性能,国内外学者提出众多提高系统稳定性的措施,并已经取得一定成果。在保护监测方面,文献[7]阐述了由于分布式电源的接入使配电网潮流流向、运行方式更加复杂,通过限制准入容量等方式改进三段式电流保护,但从长远来看依然具有局限性。在谐波抑制方面,文献[8]通过在风机与电网公共连接点加装双调谐滤波器对谐波进行抑制,以A 相电流为例,通过该滤波器对5、7次谐波抑制,使谐波畸变率由原先的13.72%降低为7.36%,起到一定滤波效果。文献[9]通过在控制环节中补偿5、7次谐波以达到抑制目的。钱克矛教授提出傅里叶滤波算法,其认为缩小窗口尺寸可抑制线性相位误差,但这种固定时间窗滤波难以满足时频特性复杂的系统[10]。小波分析可在自适应尺度上分析自身信号和噪音特征,由此小波滤波算法得到快速发展[11]。本文借鉴小波滤波算法提出了变尺度积分滤波算法,在很大程度上滤除特征谐波和一定程度的非特征谐波,减小保护因为谐波影响的误动性。
目前,直流系统中监测与保护之间的协调不够完善。本文借鉴交流系统中的阻抗三段式保护,设计直流阶梯式三段阻抗状态监测,完成快速监测、灵敏保护、协调保护之间相互协调,通过设置不同的积分滤波时长,构建阶梯式互联状态监测方式;同时积分算法兼具了滤波效果和灵敏、协调保护的时间延迟,积分时间越长窗滤波效果越明显,构成了变尺度滤波算法。最后,在PSCAD 仿真平台搭建±50kV 直流输电网仿真模型,验证该保护的正确性。
1 50 kV 直流输电网拓扑结构
1.1 直流电网拓扑结构
图1为本文研究的含分布式风电多端网状中压直流电网的拓扑结构,系统额定电压50kV,额定电流0.6kA,主要包括交流系统S1和S2、换流器(包括整流器和逆变器)、DC/DC装置、线路两端诸多分布式风力发电及输电线路等。对图中各个端口进行编号T1—T16;L1—L12表示含有正负双极的配电线路,L1—L8 为架空线路,L9—L12 为电缆线路;实线路表示正极、虚线路表示负极;f1、f2分别表示直流线路通常遇到的2种故障类型,单极接地和极间短路故障[12]。
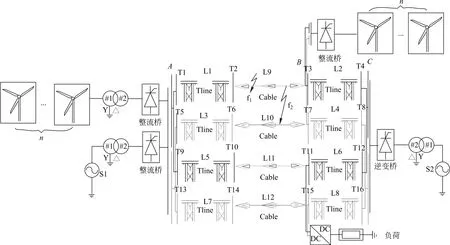
图1 含分布式风力发电的直流电网拓扑结构Fig.1 DC grid topology with distributed wind power generation
1.2 阻抗状态监测误差条件
随着电力系统日益复杂化,对系统阻抗监测的要求逐渐提高。阻抗监测可通过反应故障点到保护测量点之间的阻抗,根据测量阻抗与整定阻抗之间的关系而确定系统运行状态的监测装置,该监测方式要求准确判断监测区域的运行状态。根据文献[13],阻抗监测正确判别的条件是:定位误差ε不大于整定阻抗Zset与测量阻抗Zf之差的绝对值。如图2 所示,图中纵坐标εmax表示允许最大定位误差[13]。
由图2可知,故障定位误差允许误差最大值出现在线路出口处,误差允许值随线路延伸逐渐减少,快速段末端发生故障时,需要较高的测距精度以区分区内、区外故障;而越靠近线路首端,测距误差允许值越大。
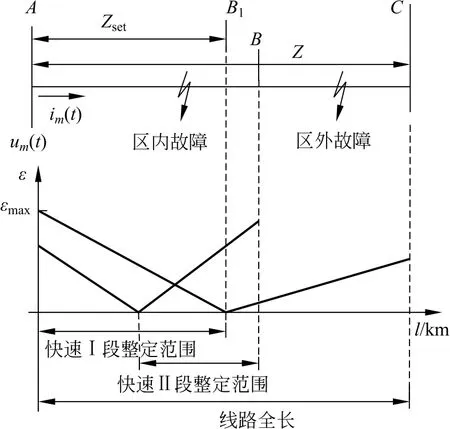
图2 定位误差与测量阻抗之间的关系Fig.2 Relationship between positioning error and measurement impedance
2 系统谐波特性分析与变尺度滤波
2.1 谐波特性分析
分布式风力发电经换流器接入直流线路,换流器具有非线性特性,在正常运行时会产生大量谐波,对继电保护和通信都会造成干扰。本文整流侧采用换相换流器(line commutated converter,LCC)。LCC通过12个换流阀进行开关断,使其在直流侧产生12k(k=1,2,3,……)次特征谐波和一些非特征谐波[14]。本文仅对直流侧的电压谐波分量进行分析,直流侧的第h次特征谐波电压有效值为
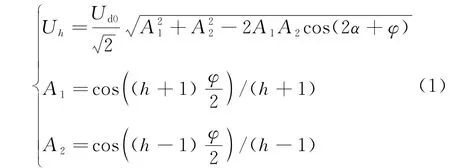
式中:Ud0为整流电压;令触发角α=0°;换相角φ=30°[15]。
2.2 变尺度滤波
本文针对含分布式风力发电的直流输电系统,结合定尺度和小波分析的多尺度滤波算法提出变尺度滤波算法。换流器交流侧谐波以m=12k±1次为主,正序分量在直流侧产生|m-1|次谐波,负序分量在直流侧产生|m+1|次谐波,即交流侧谐波会传递到直流侧11、13次谐波,其周期T11=1.8ms,T13=1.5ms;12 次特征谐波周期T12=1.67ms。凡积分大于半周期均具有滤波效果,暂定灵敏段取其较高次谐波周期的整数倍;协调段按含量最多的12次特征谐波整定,即T=3/6.7ms。本文暂定变尺度滤波时长分别为0.25、3.00 和6.70ms,250μs积分具有平滑波形的作用,仅对含量较少的高次谐波有效。对于特征谐波主要依靠于较长时间的3、6.7ms积分滤除。以特征谐波谐波为例,分别计算各次谐波经3、6.7ms积分滤除后的谐波电压剩余率如表1所示。再根据各次谐波有效值计算总体谐波总量的有效值,其表达式为
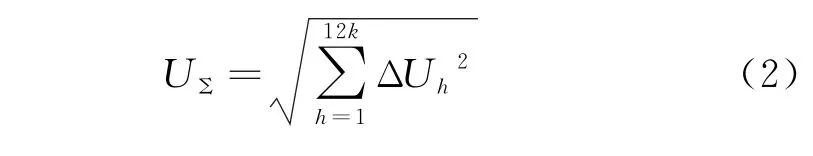
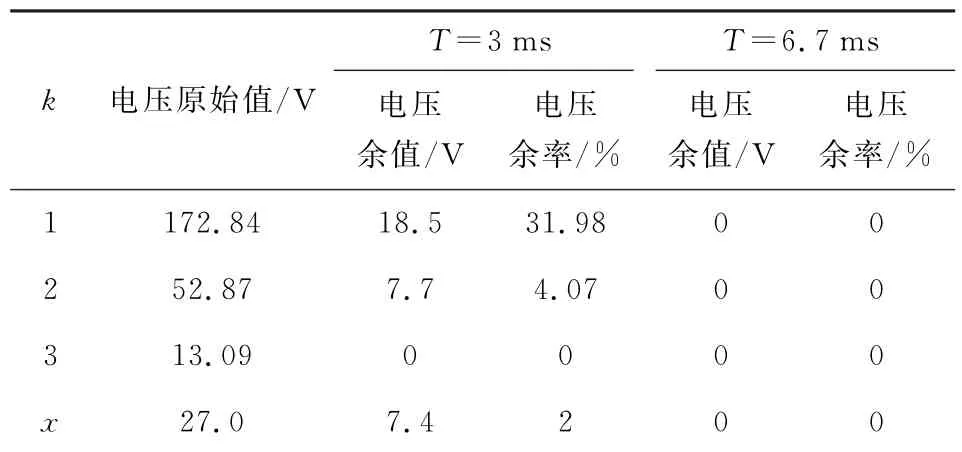
表1 积分算法剩余率值Table 1 Integral algorithm residual rate value
将表1结果带入式(2)可得:T=3ms时,U∑=32.30V;T=6.7ms时,U∑=0V。谐波有效值随积分增加而减小,滤波效果较好。
2.3 谐波电流特性
含分布式风力发电的直流系统中不仅电压量中存在谐波,电流量中同样存在谐波。在系统正常允许时,对12脉动整流器直流电流进行傅里叶分解,其结果如图3所示。其正常情况电流主要谐波次数与电压相同,以12的整数倍为主,其总占比在15%以内[16]。
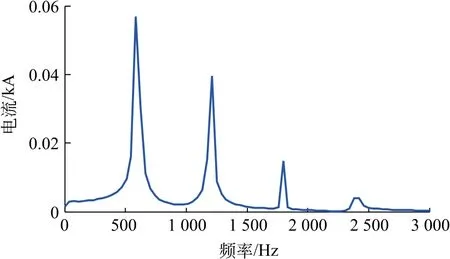
图3 正常谐波电流含量Fig.3 Normal harmonic current content
当直流系统发生短路故障时,故障极电压降低,电流迅速增大。因其电压降低,故障电压中的谐波有效值也大大减小,有时可忽略;但故障电流迅速增大,成为不可忽略的因素,晶闸管不同于绝缘栅双极型晶体管,直流侧发生故障更不容易闭锁,使12的整数次谐波源源不断馈入直流侧,其次直流系统也会产生大量高频谐波,会使保护范围增大或减小。当直流侧线路出口发生金属性单相接地故障时,对发生故障后的故障电流进行傅里叶分解,如图4所示。谐波含量增多,进行3ms积分滤除处理后,结果如图5所示,谐波含量减小,此处不再验证6.7ms积分滤除效果,理论上可以滤除所有高频信号。
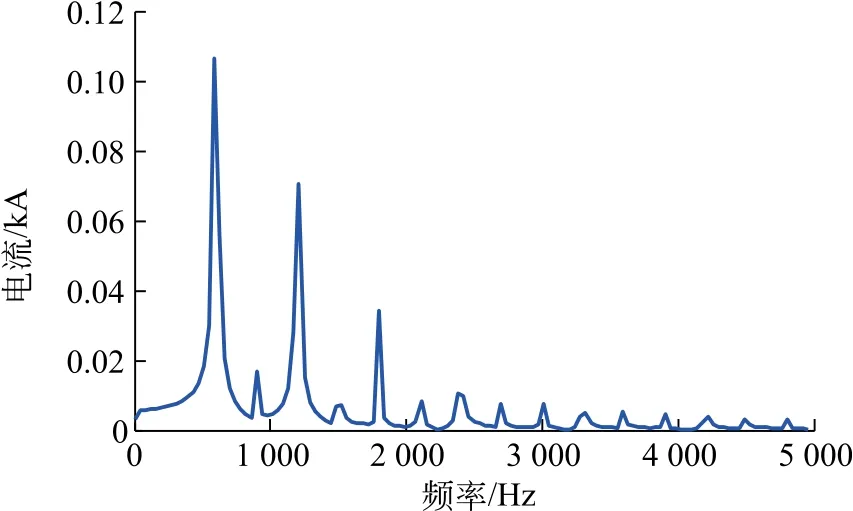
图4 故障谐波电流含量Fig.4 Fault harmonic current content
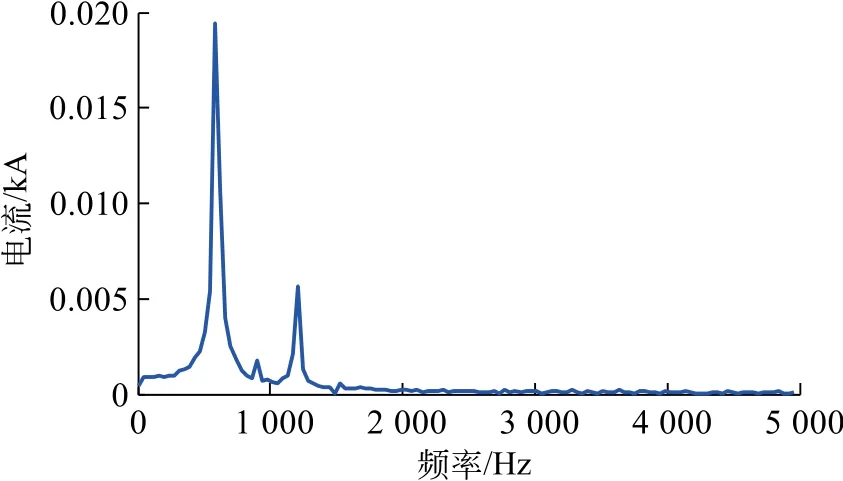
图5 3ms滤波处理后故障谐波电流含量Fig.5 Fault harmonic current content after 3ms filtering
3 系统监测特性分析
本文以监测为手段,以保护为目标展开研究。阻抗快速监测段基于极短时间窗积分,较小阈值用于监测系统严重故障,较大阈值用于监测系统不正常运行状态;灵敏段保护和协调段保护针对轻微故障滤除谐波干扰而进行判定故障。本文利用较为完善的阻抗保护特性来监测和保护线路运行状况,可应用于含分布式风力发电的直流系统中。为了分析系统阻抗监测特性,将以图6为例,分别对系统阻抗监测的快速段、灵敏段、协调段进行分析。
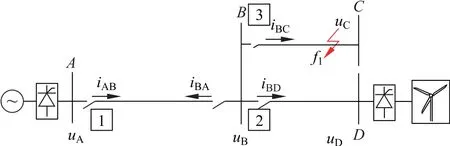
图6 直流系统仿真模型Fig.6 DC system simulation model
3.1 阻抗快速监测分析
根据图2 可知,按照传统的阻抗判据,即便于B1点可以准确判别故障,B1B也将由阻抗灵敏段保护识别切除,需要增加时间延迟,在一定程度上降低保护的灵敏度。系统中存在大量电力电子器件,系统会因B1B段判别所加的时间延迟而崩溃,鉴于上述情况,本文在传统距离Ⅰ段的基础上,加入快速监测Ⅱ段。如图2虚线所示,利用下一级线路出口电压uB(t)及线路电流iBA(t)=-iBC(t)-iBD(t),计算本级反向阻抗,其测量误差允许值由B1至B逐渐增加,可以弥补快速监测Ⅰ段至灵敏段监测的不足,故阻抗快速监测Ⅰ段和Ⅱ段整定如下。
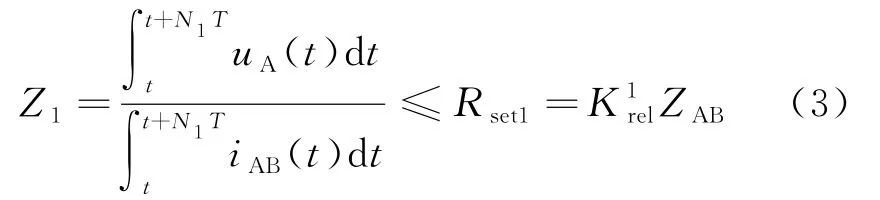
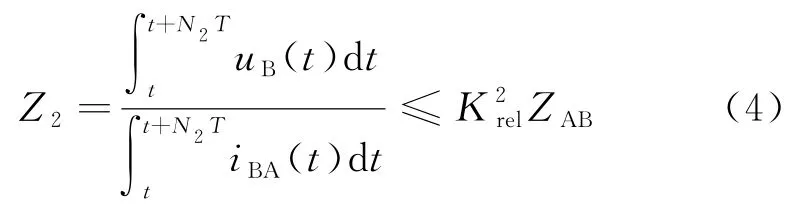
在直流系统发生故障瞬间,电容放电使电流急剧增大,电压急剧减小,会造成瞬时测量阻抗较低的情况,为了保证方法的可靠性,本文采用
本段采用五点积分,仅起到消除个别极端误差点的作用,对谐波特性保留相对完整。在50kV 直流系统中,电压允许偏差极限-15%~+5%[17],功率偏差极限+15%~-20%[16],当电压和功率取偏差上极限得到此时电流允许误差,以该线路50kV、0.6kA 情况下,测量阻抗为72.81Ω;各个参数取下极限时,测量阻抗为75.35Ω。设定当监测到的该线路阻抗Z1≤Zk≤75.35Ω,即系统可能存在不正常允许状况,此时仅发出警告而不跳闸。
综合上述分析,快速监测Ⅰ段和快速监测Ⅱ段相互配合监测本级线路所有状况,当直流线路发生故障时,其测量阻抗低于任意门槛值,断路器动作切除故障线路;当系统发生不正常非故障允许状态时,亦可发出信号警示,以便值班人员及时调整。其逻辑如图7所示。
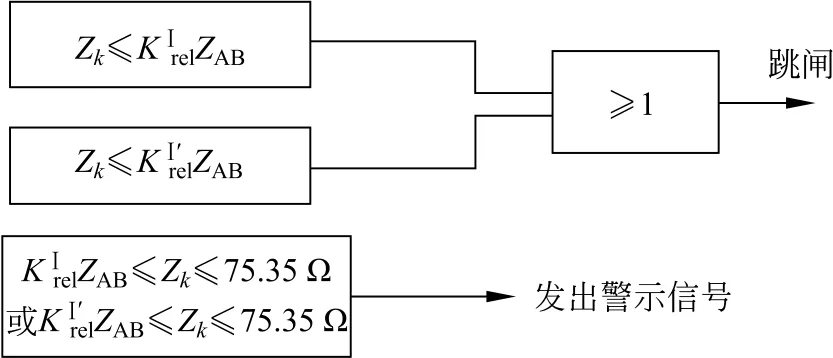
图7 阻抗快速监测逻辑Fig.7 Impedance fast monitoring logic
3.2 阻抗灵敏段保护分析
阻抗灵敏段保护按照与相邻线路快速监测相互配合整定,但在新能源加入的多电源电力系统中,分支系数的出现影响阻抗的整定和灵敏度校验[18]。如图3所示,BC线路中发生故障,保护1的阻抗灵敏段实际电压UA为
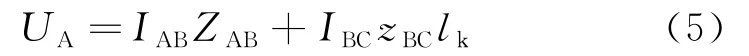
式中:ZAB为线路AB阻抗;zBC为线路BC单位阻抗;lk为故障点至B母线距离。
保护1的测量阻抗为
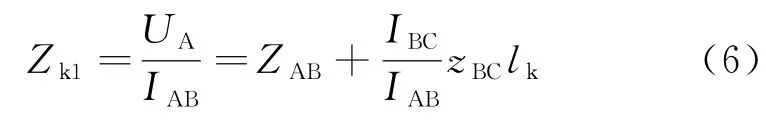
式中Kb=IBC/IAB为距离灵敏段的分支系数。保护1的实际阻抗为
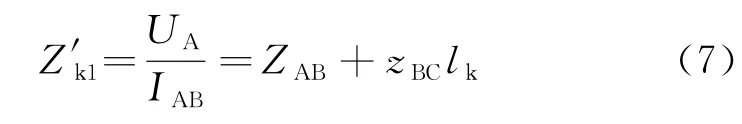
比较式(6)与式(7),因为式(7)分支系数的存在,使测量阻抗大于实际阻抗,保护范围减小。式(6)中IBC=-IBA+IBD,IBD为风力发电输入系统电流,具有很强的不确定性。当无风情况下IBD=0,Kb=0,此时Zk1=Z'k1;当风力较强时,IBD>0,Kb>1,测量阻抗增大,保护范围减小,由于风电的不确定性,使保护1的测量阻抗同样具有不确定性。为解决这一问题,本文采用实时调整Kb来避免分支系数的影响。阻抗灵敏段整定如下:
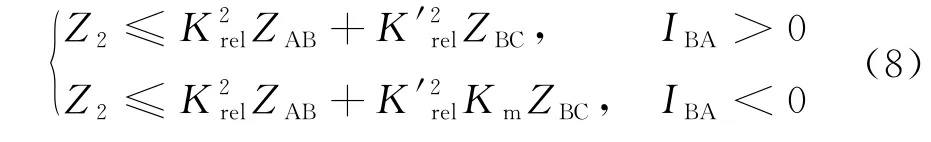
式中:Km=IAB/IBC,IBC相对于IAB会有十几ms的延迟,但是相对于距离灵敏段本应有的0.5s延迟,通信延迟可以忽略不计1.22。于此同时,Z2的整定引发新的问题,当线路存在故障时,IBC=0、Km=∞、Z2=∞,不利于保护动作。为解决此问题,将Z2分段整定,当IBA>0时,Z2按无Km进行整定,当IBA<0时,加Km系数进行整定。
3.3 阻抗协调段保护分析
阻抗协调段作为远后备保护方式,通常按最大负荷电流进行整定,其整定如下:
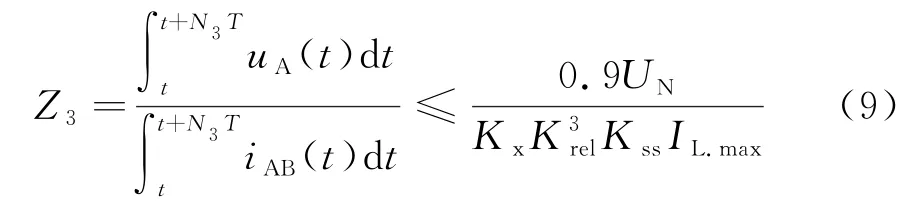
式中:额定电压UN=50kV;IL.max=700A;可靠系数;自启动系数Kss=2.5;考虑直流偏磁等因素的影响,进一步增加保护的可靠性,令Kx=2。
3.4 三段配合分析
阻抗快速监测分析、阻抗灵敏段保护分析和阻抗协调段保护分析协调关系如图8所示,图中x表示故障发生的位置,Z表示x处发生故障的测量阻抗,Zset1、Zset2和Zset3为各段的整定阻抗。本文主要研究线路AB 的保护,快速Ⅰ段正向保护线路70%,快速Ⅱ段反向保护线路70%,Ⅰ、Ⅱ段保护线路全长且留有一定余地,仅为保护固有时间,无添加延迟;灵敏段和协调段作为后备保护,分别添加0.5 s和1 s的延时,以防止越级跳闸,灵敏段可保护相邻线路的18.71%,协调段可保护所有线路。
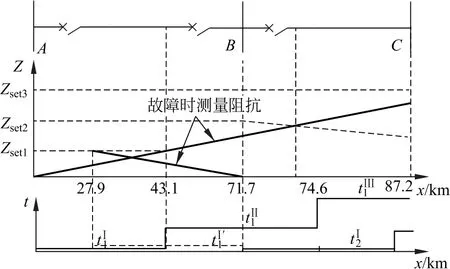
图8 阶梯保护示意图Fig.8 Schematic diagram of ladder protection
由于系统不正常运行状况过多,谐波、系统振荡、高阻接地等等,且监测每种情况所用时间需具体分析,故图中暂未标注快速段监测系统不正常运行状态情况[19]。
4 仿真验证
利用PSCAD/EMTDC 电磁仿真软件平台,搭建含分布式风电的±50kV 直流电网仿真模型,如图1所示,相关模型其他参数如表1所示,采样频率为50kHz故障发生在假设0ms(4000个点)处。
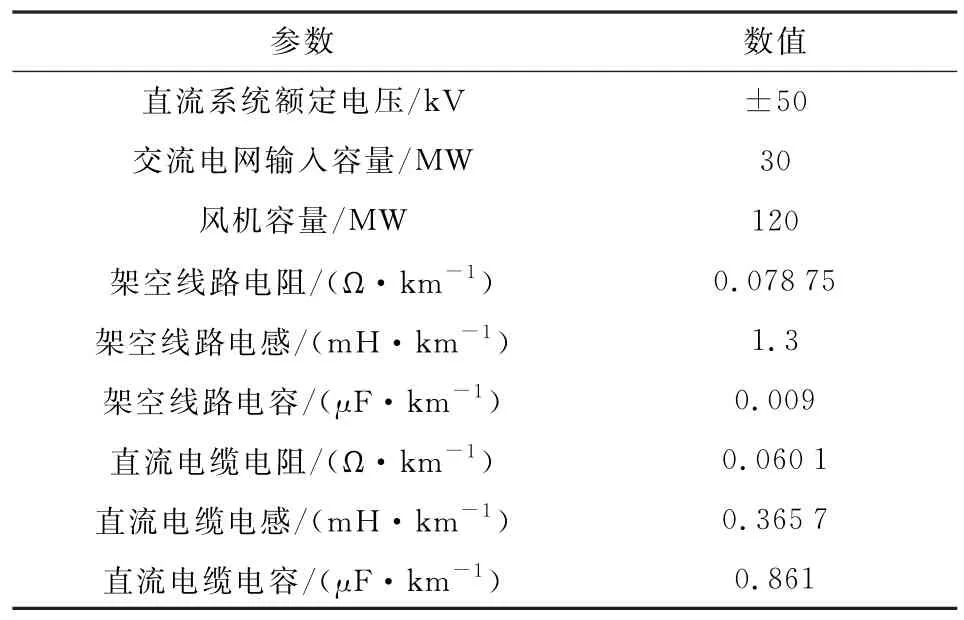
表1 直流输电网模型参数Table 1 Model parameters of DC transmission network
4.1 单极接地故障仿真
以直流输电系统AB线路首段端发生单极接地故障时为例,进行仿真验证,如图9所示,快速Ⅰ段迅速识别故障;未超过快速Ⅱ整定值;灵敏段于点4200(即故障发生10ms后)判别后需增加0.5s时间延迟方可动作;协调段于点4123(6.15ms),对于保护1跨越2级线路,判别后需增加1s时间延迟后动作。灵敏段整定值按照时变电流整定,发生故障瞬间会有尖波冲击,由于具有0.5s的时间延迟,因此对保护判别无较大影响。
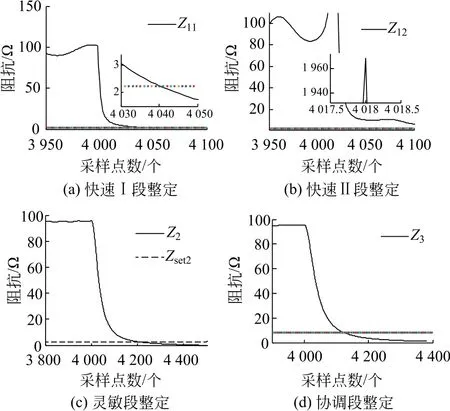
图9 AB 首端单极故障故障极仿真结果Fig.9 Simulation results of the single-pole fault at the AB head end
对于健全极,仿真结果如图10所示,其测量值均远远高于整定值,健全极各段均可靠不动作。
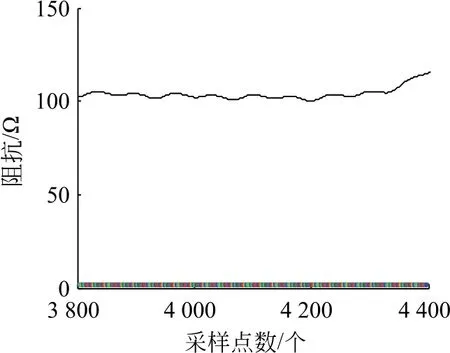
图10 AB 首端单极故障健全极仿真结果Fig.10 Sound pole simulation results of AB head-end single-pole fault
4.2 各段协调配合仿真
对系统特殊节点进行仿真,如表2所示,表中第1列表示故障点至线路AB首端的距离,中间数据为发生故障后多久可以判别故障。其中,1-Ⅲ数据最小,判断速度最快;1-Ⅰ、2-Ⅰ其次;1-Ⅱ最慢;这是因为1-Ⅰ、2-Ⅰ时间窗最短,不能完全避免发生瞬间的短暂冲击,造成测量阻抗略小于实际阻抗,经仿真验证,其影响较小,最严重故障情况也可避免越级跳闸。经对比表2数据与图8相吻合。可实现各段的阶梯配置。
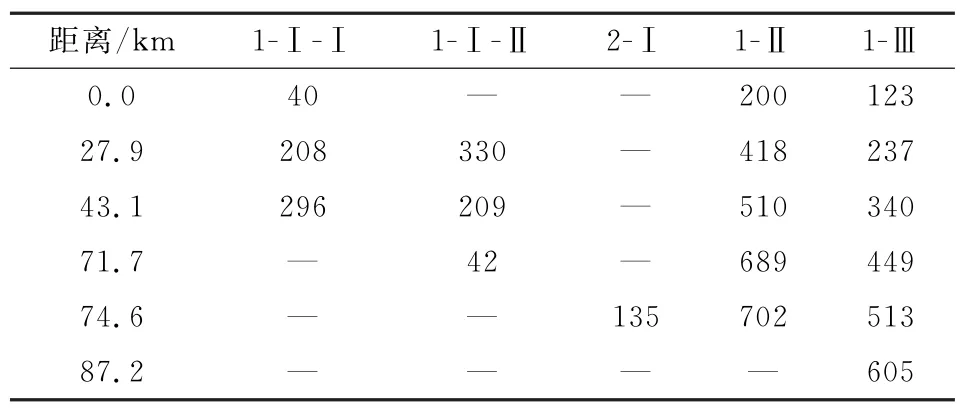
表2 关键节点仿真数据Table 2 Key node simulation verification data
5 结论
本文针对含分布式风力发电接入的直流电网使系统谐波增加提出的阶梯式阻抗监测方案,设置不同的相适应的积分时间,形成互联阶梯阻抗监测方案,通过分析得到以下结论:
1) 快速监测Ⅰ段和Ⅱ段相互配合,监测线路全长,通过设置两段阈值,可以发现系统严重故障后迅速切除,亦可发现系统不正常运行状态。
2) 灵敏段保护可以保护监测线路全长及相邻线路的一部分,为本级线路的近后备保护,该段也解决了汲出系数影响。
3) 协调段保护可做相邻线路的远后备保护,将含量最多的某次谐波积分一周期,滤除系统中大多数谐波,可靠性最高。
本文运用的最原始单端电气量,简单可靠,无需考虑通信延迟影响,该积分算法反应故障积累过程,可以有效对抗谐波影响。最后,通过PSCAD 验证了该方案具有工程推广价值。

