基于线性化的交直流混合配电网运行优化
罗泽宇江岳文
(福州大学电气工程与自动化学院,福建省 福州市 350108)
0 引言
随着传统化石能源呈现衰竭趋势,全球范围内对新能源及其发电技术的需求日益增加。在配电系统中,越来越多的新能源并入电网,如风电、光伏、电动汽车和储能等,因此未来的配电系统必须包括额外的直流负载和基于直流的分布式电源(distributed generation,DG)[1]。而DG 相比于并入现有的交流电网,将其并入直流配电网能够有效减少换流站的投资,同时能够减小换流过程的损耗,具有很大的经济效益。此外,传统交流配电网缺乏灵活控制功率潮流和网络拓扑的手段[2],大量DG 接入后容易导致弃风弃光现象,因此未来的配电系统应该成为交直流混合系统,实现高比例可再生能源的消纳和多种直流负载的接入[3]。
交直流混合配电网需要换流设备将交流和直流部分互联,基于电压源换流器(voltage source converter,VSC)的换流技术应用在交直流混合配电网当中有着诸多优点[4-5],因此含VSC 的交直流混合配电网优化运行是目前研究的一个热点。文献[6]提出以网损最小、电压偏移量最小、系统静态电压稳定裕度最大及供电能力最大的多目标交直流混合系统优化模型。文献[7]通过自适应修正换流站功率参考值和下垂系数实现无功优化。文献[8]根据节点电压是否越限将配电网运行状态分为正常和风险2种状态,分别建立换流器功率优化模型。文献[9]提出变换器分级功率均分的控制策略,改善电网中各电力电子变换器的长期运行寿命的均衡性。但是以上研究多集中在以发电费用最小或降低网损、改善电压质量为目标,缺少对DG、VSC和储能等设备的联合优化进行分析,因此文献[10-13]对含DG和储能的交直流混合系统的优化进行了研究。交直流混合系统优化模型为混合整数非线性规划(mixed integer nonlinear programming,MINLP)问题,目前的求解方法主要包括线性规划法[12-13]、二阶锥规划方法[14]、启发式算法[15-17]。二阶锥规划虽然存在全局最优、求解速度快的优点,但是大多应用在辐射型配电网,在环网中使用二阶锥松弛条件苛刻,不一定能满足松弛的精确性[18-19],因此不具有通用性;文献[12]提出的线性化方法忽略了线路的损耗,导致其模型误差较大;文献[13,20]的线性化方法基于运行点进行迭代,精确性较高,但是需要获得系统运行过程中的断面数据进行多次迭代,计算过程复杂;启发式算法存在全局最优性难以保证,求解效率低下等问题。
为克服以上存在的问题,本文提出一种基于线性化的含DG、VSC 和储能的交直流混合配电网运行优化模型,将MINLP 问题转化为混合整数线性规划(mixed integer linear programming,MILP)问题进行高效、快速求解,该模型不仅能够应用在辐射型配电网当中,也能应用在环形等其他拓扑形式的配电网,相比于二阶锥松弛技术更具有适用性,同时计及了输电线路和VSC的损耗,在提高计算速度的同时保证计算精度。
1 交直流混合配电网稳态模型
交直流混合配电网稳态模型包括VSC 换流站模型、直流配电网模型和交流配电网模型,交流配电网和直流配电网通过VSC 进行互联。本文以2台VSC对交流配电网和直流配电网进行互联的双端交直流混合配电网为例进行研究,其结构如图1所示。
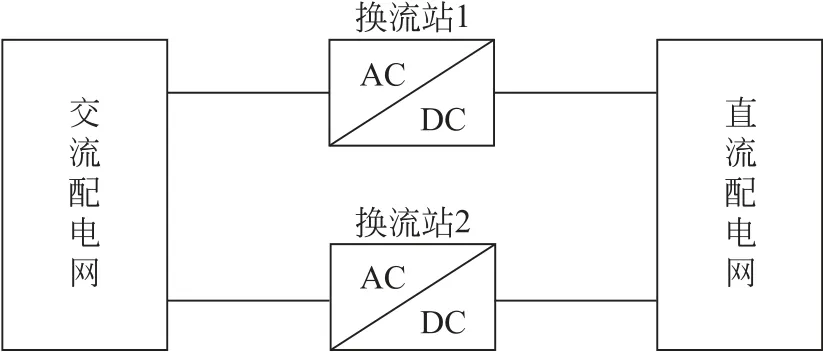
图1 双端交直流混合配电网结构Fig.1 Structure diagram of the double-ended AC/DC hybrid distribution network
1.1 VSC 换流站及控制方式
基于VSC的换流站稳态模型结构如图2所示。
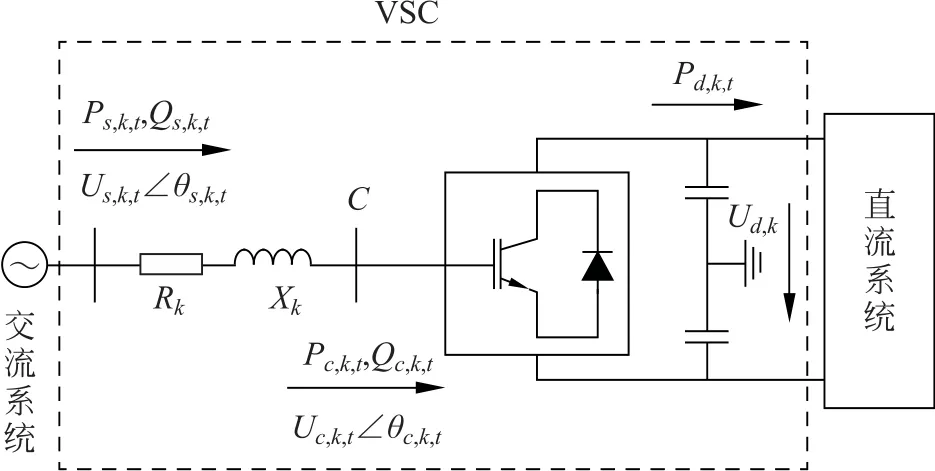
图2 VSC换流站模型结构Fig.2 Structure diagram of VSC converter station model
图中C点左侧为换流变压器等效模型,C点右侧为理想换流桥,换流变压器和换流器内部的损耗等效到电阻Rk中。为便于讨论,令δk,t=θs,k,t-θc,k,t,αk=arctan(Xk/Rk),则VSC 的稳态方程为:
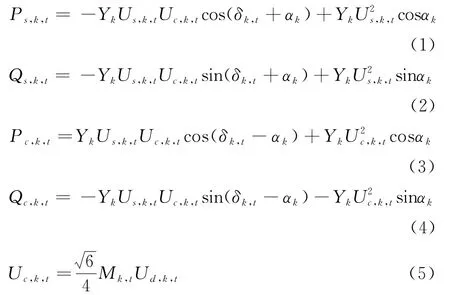
式中:k为接入系统的第k台VSC;Ps,k,t和Qs,k,t分别为交流系统注入换流变压器的有功功率和无功功率;Pc,k,t和Qc,k,t分别为换流变压器流入换流桥的有功功率和无功功率;Us,k,t为换流变压器与交流系统连接处的节点电压幅值;θs,k,t为换流变压器与交流系统连接处的节点电压相位;Uc,k,t为C处的电压幅值;θc,k,t为C处的电压相位;Xk为换流变压器的电抗;Rk为VSC 内部损耗和换流变压器损耗的等效电阻;Ud,k,t为VSC 直流侧的输出电压大小;Mk,t为VSC的调制度[21]。
同时,VSC注入直流网络的有功功率Pd,k,t为

不同VSC控制方式下交直流混合配电网的运行状态不同,VSC的控制方式一般分为:(1)定直流电压、定交流无功控制;(2)定直流电压、定交流电压控制;(3)定交流有功、定交流无功控制;(4)定交流有功、定交流电压控制;(5)下垂控制。本文采取的VSC 控制策略为定交流有功、定交流无功控制,其控制方程为
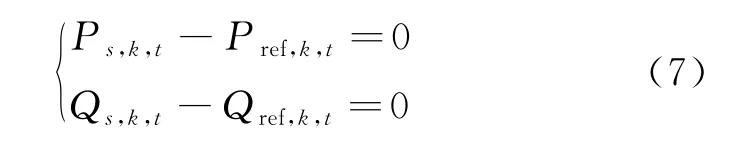
式中:Pref,k,t和Qref,k,t分别为VSC 有功功率、无功功率整定值。在优化模型中,VSC 的整定值Pref,k,t、Qref,k,t根据优化结果进行修正,实现对系统潮流的调控。
1.2 交流配电网模型
交流配电网的Distflow 潮流模型为:


1.3 直流配电网模型
根据交流配电网Distflow 潮流模型的建模方法,可推导出直流配电网的潮流模型如下:

2 交直流混合配电网运行优化模型
2.1 目标函数
在含有分布式电源、储能和VSC的交直流混合配电系统中,可以通过优化本级配电网向上级主网的购电量、储能的充放电策略和换流站的有功和无功功率,实现网损的减小和可再生能源的充分消纳,从而降低交直流系统的综合运行成本。因此本文以向上级主网购电的成本、弃风弃光成本、网损成本和储能日运行维护成本之和最小为目标函数,具体为:
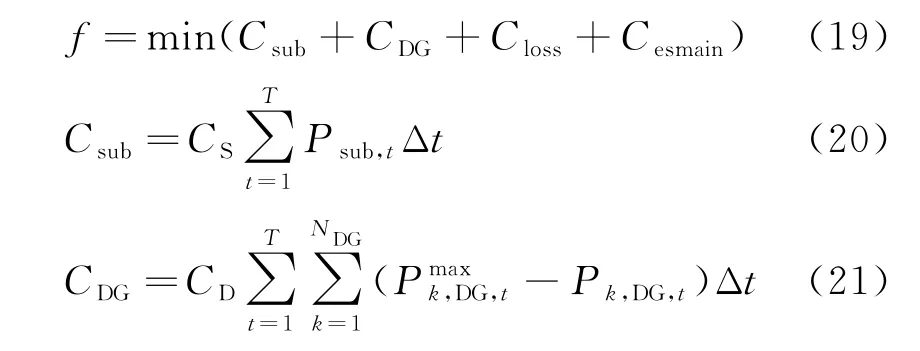
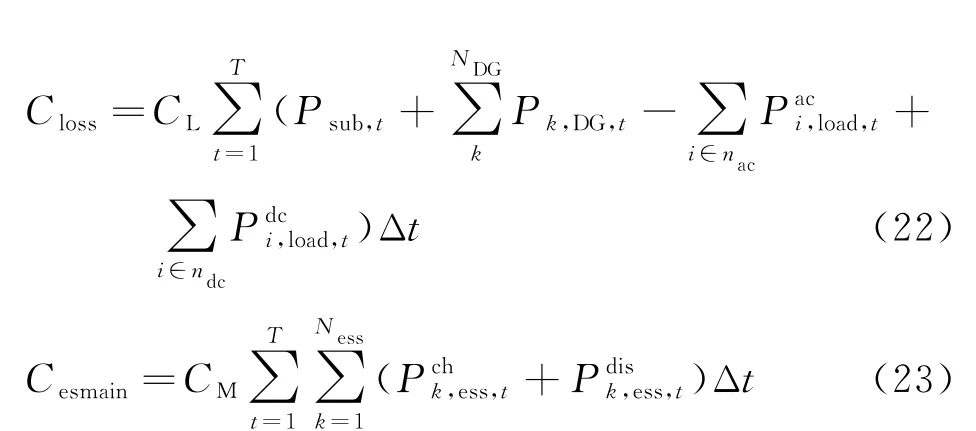
式中:Csub、CDG、Closs、Cesmain分别为向上级主网购电成本、弃风弃光成本、网损成本和储能日运行维护成本;CS、CD、CL、CM分别为上级主网电价、单位弃风弃光成本、单位网损成本和储能单位充放电量的运行维护成本;Psub,t为上级电网向本级配电网输送的功率为第k台DG 的可出力最大值;Pk,DG,t为第k台DG 的实际出力分别为第k个储能系统的充放电功率;NDG为DG的台数;Ness为储能系统个数;nac为交流节点集合,ndc为直流节点集合;Δt为时间间隔;T=24。
2.2 约束条件
(1) 潮流约束。
交直流混合配电网的潮流约束由式(1)—(3)、(5)—(18)构成。
(2) 系统安全运行约束。
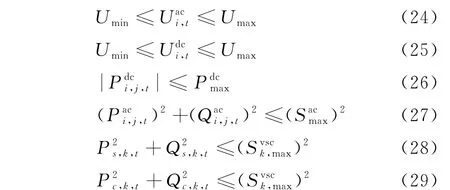
式中:Umax和Umin分别为节点电压上下限为交流线路最大传输容量为直流线路最大传输功率为第k台换流器容量。
式(24)描述了系统电压的安全运行范围;式(26)(27)描述了线路的传输功率限制;式(28)(29)描述了换流器传输功率限制,由于换流器的功率可以双向调节,因此无论功率是从交流系统流入换流桥,还是从换流桥流入交流系统,都要在换流器的容量限制范围内。
(3) 变电站功率约束。
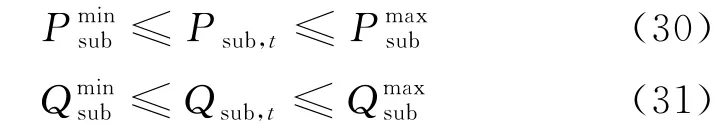
(4) 电源出力约束。
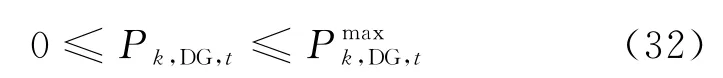
(5) 储能运行约束。

式(33)—(35)为储能充放电功率约束,式(35)表示同一台储能在同一时刻不能既充电又放电,式(36)和(37)为储能荷电状态约束,式(38)表示储能在一个运行周期内充放电量平衡。式(39)和(40)表示储能充放电标志位为0-1变量。
2.3 模型线性化
式(1)—(3)、(5)—(40)构成的交直流混合配电网优化模型中潮流方程是非凸非线性的方程,导致该模型本质上是一个MINLP问题。本文通过一系列线性化方法,将该MINLP 问题转化成MILP问题,能够调用线性规划求解器高效求解,在保证全局最优的情况下提高了计算速度。
(1) 交流配电网潮流模型线性化。
交流配电网模型的非线性源来自于式(10)—(12)。同时注意到,在式(24)中令Umin=0.95、Umax=1.05,则全网的节点电压可以表示为

式中δ∈[-0.05,0.05],为一个足够小的数,故进一步满足如下关系:
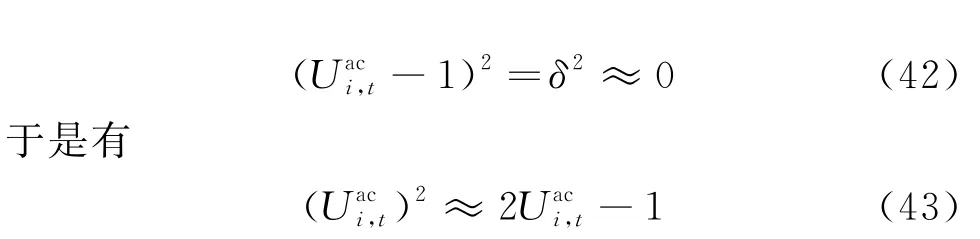
将式(43)代入式(10)中并忽略高次项,得到电压方程的线性形式:
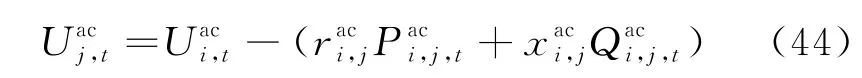
稳态运行下,电力系统全网的节点电压在基准电压附近,因此对于式(11)(12),令则网损可以表示为:
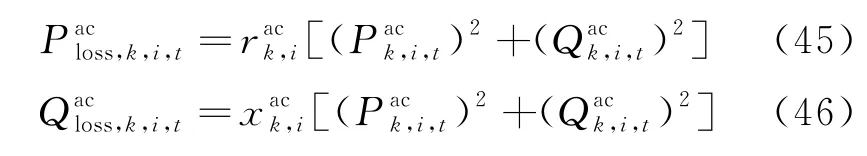
(2)直流配电网潮流模型线性化。
直流配电网模型的非线性源来自于式(16)(17),参照交流配电网模型的线性化方法,得到其线性化方程为:
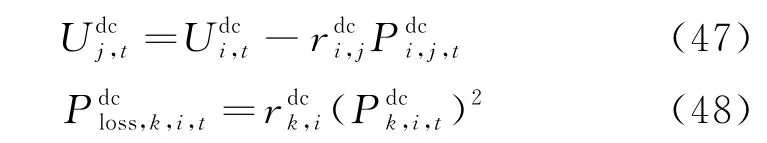
(3) VSC模型线性化与交直流系统的互联。
在图2 所示的VSC 模型中,基于C点可将VSC模型划分为交流部分和直流部分。换流变压器部分可以归到交流系统中进行计算,因此可以将VSC模型当作有向的交流支路进行处理;另一方面,理想换流桥可以为直流系统双向传输功率,因此在直流系统中也可以将VSC 模型当作有向的直流支路进行处理。为便于描述,将图2中的C点称为VSC节点,于是有
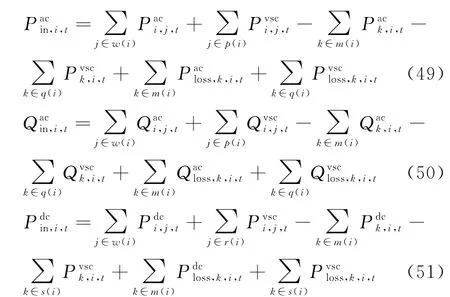
式中:p(i)为以交流节点i为首端节点的末端VSC节点集合;q(i)为以交流节点i为末端节点的首端VSC节点集合;r(i)为以直流节点i为首端节点的末端VSC节点集合;s(i)为以直流节点i为末端节点的首端VSC 节点集合分别为VSC支路ij和ki传输的有功功率分别为VSC支路ij和ki传输的无功功率和分别为VSC支路ki的有功损耗和无功损耗。
如果VSC支路的方向是从交流系统指向直流系统,即支路方向为i→j,j∈p(i),则VSC 电压方程为
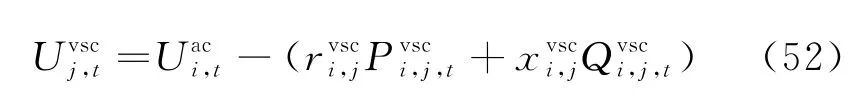
如果VSC支路的方向是从直流系统指向交流系统,即支路方向为k→i,k∈q(i),则VSC电压方程为

在式(5)中,由于0≤Mk,t≤1,则式(5)可以等效为

至此统一了VSC 模型与基于Distflow 潮流形式的交直流配电网模型。
(4) 线路潮流约束线性化
式(28)(29)可以用式(56)替代
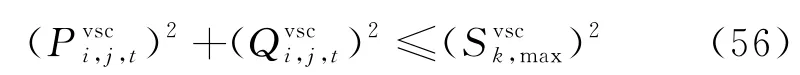
式(27)和式(56)表示的载流量约束在数学上表示的是1个圆的内部,用1个圆内接正十二边形来近似表示这个圆,从而式(27)和(56)所表示的非线性约束可以被以下一系列线性约束替代:
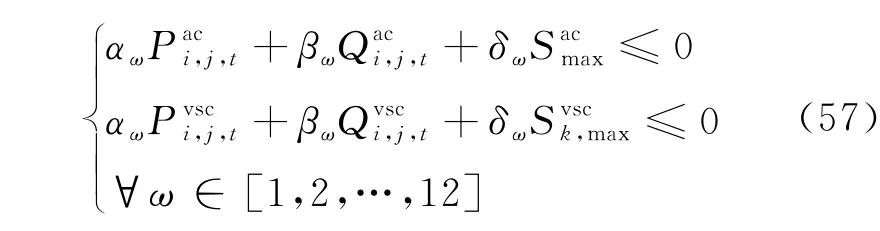
式中:αω、βω、δω为线性化载流量约束系数,其数值可参考文献[12]。
对于式(45)(46)(48)中的平方项,可以用分段线性化[22-23]进行处理,于是最终转化为如下的MILP模型,调用YALMIP工具箱下的CPLEX 求解器进行求解。

3 算例分析
3.1 算例数据
算例以改造的13节点拓扑结构作为交直流混合配电网模型为基础进行分析计算,结构如图3所示。该系统1—6节点为交流节点,构成交流配电系统,7—13节点为直流节点,构成直流配电系统。交流配电网和直流配电网通过VSC1和VSC2这2台VSC换流器互联,VSC1连接交流节点2和直流节点7,VSC2连接交流节点6和直流节点10。交流节点2通过变电站连接上级主网,直流节点8、11和13接入光伏,直流节点9通过VSC3换流器接入风电,VSC3起并网整流器作用,控制方式为定交流有功、定交流电压控制。系统基础数据见表1,电源参数见表2。

表1 交直流混合配电系统基础数据Table 1 Basic data of AC/DC hybrid power distribution system

表2 交直流混合配电系统电源容配置情况Table 2 Power capacity configuration of AC/DC hybrid power distribution system MW
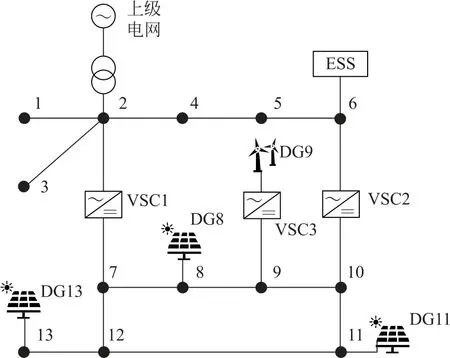
图3 改造的13节点交直流混合配电网结构图Fig.3 Structure diagram of the modified 13-node AC/DC hybrid distribution network
3.2 优化结果分析
在交直流混合配电网的实际运行当中,换流器不仅可以双向调节传输的有功功率,还可以作为无功补偿装置发出感性或容性的无功的功率,改善电压水平,降低系统网损,促进DG 出力的消纳,因此VSC能够和储能互相配合,实现交直流混合配电网运行的优化。
(1) 多时段优化运行结果。
交直流混合配电网优化运行结果由图4—6给出。图4给出了系统总负荷、系统有功网损、向上级主网的购电功率和DG 出力的时序值,图5给出了储能的荷电状态曲线,图6给出了2台VSC的有功传输功率和无功出力情况。
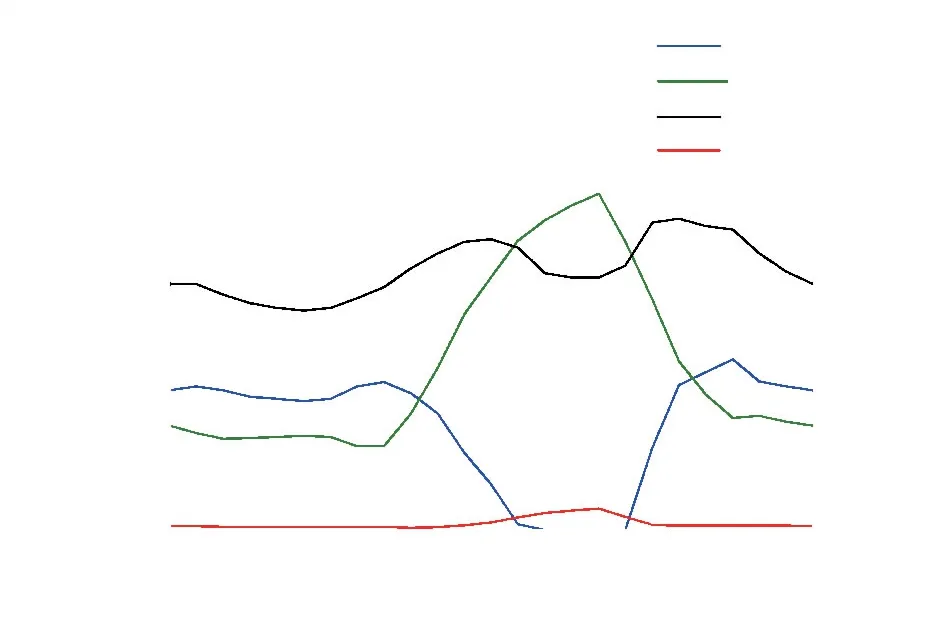
图4 负荷、网损、购电功率和DG 出力时序值Fig.4 Load,network loss,purchased power and DG output timing values
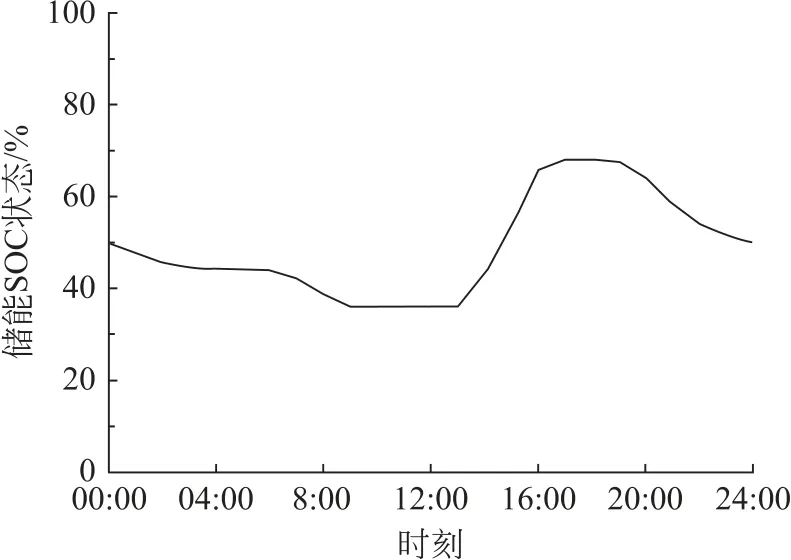
图5 储能荷电状态Fig.5 Energy storage state of charge
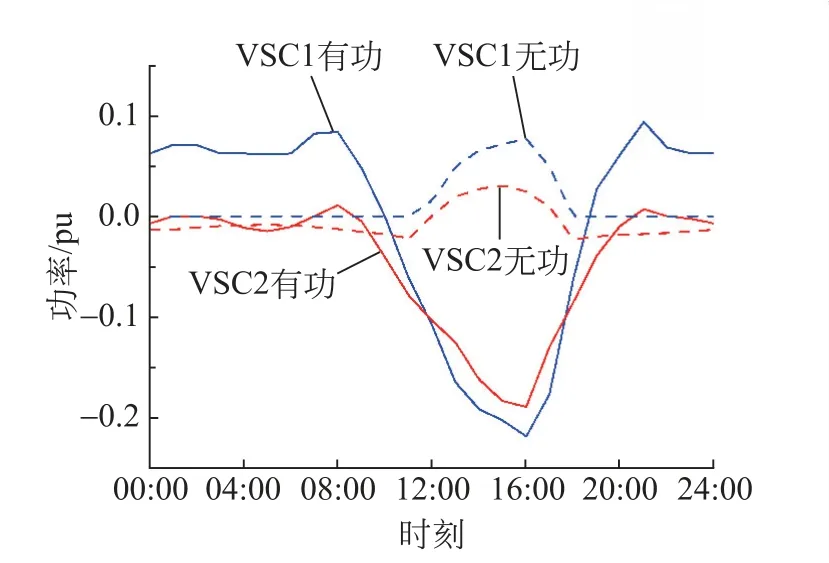
图6 VSC功率曲线Fig.6 Power curve of VSC
由图4可以看出:00:00—13:00系统的总负荷水平高于DG 最大出力,此期间DG 和变电站共同向负荷供电,结合图5可知此期间储能系统处于放电状态,但放电功率较小;13:00—17:00系统的总负荷水平低于DG 的最大出力,此时系统向储能充电以消纳DG,减少弃风弃光成本;17:00—24:00运行情况与00:00—13:00相似。
在图6中,有功曲线大于0表示VSC传输的有功功率由交流系统流入直流系统,小于0则相反;无功曲线大于0表示VSC吸收感性的无功,小于0表示VSC 发出感性无功。结合图4、6 可以看出,13:00—17:00由于DG 的出力高于负荷,且都配置在直流配电网当中,因此当DG 向位于交流节点6的储能充电时2台VSC 流经的有功功率高于其他时刻。同时,此时段内VSC从交流系统吸收感性无功以促进DG 的消纳。
(2) 储能和VSC 无功补偿能力对优化结果的影响。
为分析储能的配置和VSC 的无功补偿能力对优化结果的影响,分别设置如下4种优化策略进行对比:无储能无VSC无功补偿、有储能无VSC无功补偿、无储能有VSC无功补偿、有储能有VSC无功补偿,分别对应策略1 至策略4,对比结果由表3给出。
由表3可以看出,系统在无储能且没有VSC提供无功补偿装置的情况下总成本最高,其次为策略2,然后是策略3,储能和VSC 联合优化时系统总成本最低。
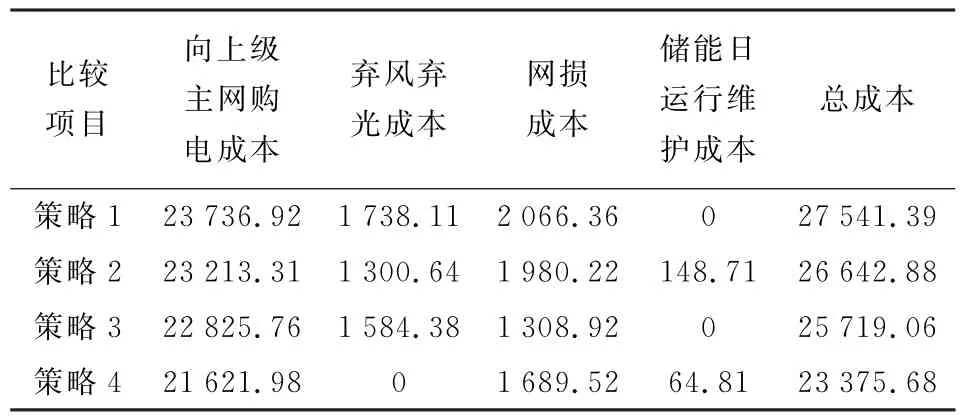
表3 储能和VSC无功补偿对运行成本的影响Table 3 Influence of energy storage and VSC reactive power compensation on operating costs 元
由此可以得出,在配电网中储能主要起到降低弃风弃光成本的作用,VSC 的无功补偿主要起到降低网损的作用,另一方面,VSC 的无功补偿还可以改善因DG 出力过高引起的电压越限,实现DG 的充分消纳,因此储能和VSC联合优化才能使配电网的弃风弃光成本降到最低。
(3) 线性化模型误差分析。
为验证本文所提线性化方法的准确性,将线性化模型的计算结果与内点法计算结果进行对比,结果如表4所示。
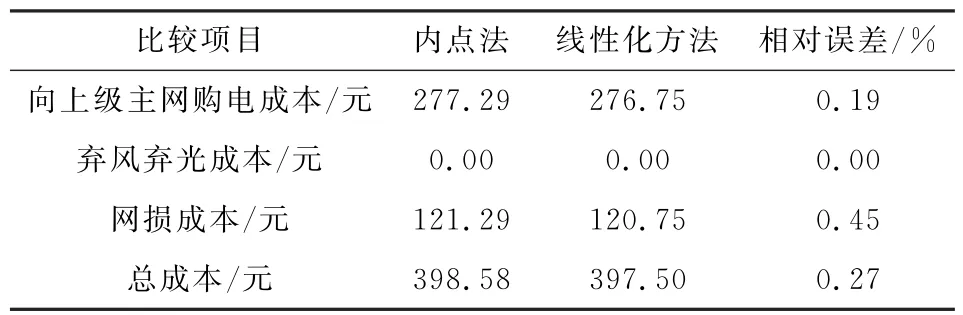
表4 线性化模型精度对比Table 4 Linearized Model Accuracy Comparison
在交直流混合配电网优化模型中,储能本身是一个线性模型,对模型线性化并无影响,因此本文取网损最高的16:00时刻,将该时刻多余的风光出力倒送回上级主网,以单时段优化结果进行分析。表4给出了线性化方法与内点法运行成本的对比,图7为2种方法计算出的各节点电压幅值相对误差。
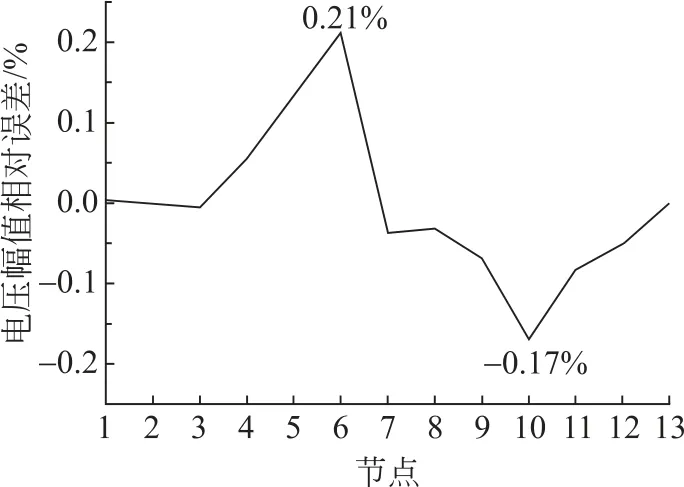
图7 节点电压幅值相对误差Fig.7 Relative error of node voltage amplitude
由表4可以看出,线性化模型目标函数相对误差最高为0.45%,由图7可知节点电压幅值相对误差最高为0.21%,为10-3数量级,因此本文所提线性化模型有较高的精度。
表5列出了在单时段优化中运用内点法和线性化方法进行优化的时间比较。由表5可知,与内点法相比,线性化方法具有显著的计算时间优势,更加适用于应用在交直流混合配电网的优化运行当中。

表5 线性化方法与内点法优化时间比较Table 5 Comparison of optimization time between linearization method and interior point method
4 结论
对于含有DG、VSC 和储能的交直流混合配电网,本文以配电网购电成本、弃风弃光成本、网损成本和储能日运行维护成本之和构成的系统综合运行成本最小为目标构建其优化模型,优化配电网购电量、VSC功率和储能充放电策略以实现配电网的经济运行。提出了一种线性化方法对优化模型进行转化,将MINLP 问题转化为MILP 问题进行求解,该方法不仅能够得到全局最优解,而且考虑了网损,具有较高的精度,同时没有网架拓扑形式的限制,适用于更多场合下的电力系统优化。

