基于虚拟元方法求解端部受抛物线荷载的悬臂梁问题

马俊驰, 梁晓坤, 索宇洋

(辽宁师范大学 数学学院, 辽宁 大连 116029)

悬臂梁是材料力学研究中的重要内容之一, 广泛应用于建筑工程[1]、电子工业[2]、机械工程[3]等. 关于悬臂梁的研究一直备受关注. 2010年, Yao[4]研究了四阶边值问题(即悬臂梁方程), 证明了一类奇异四阶两点边值问题正解的局部存在性定理. 文献[5]利用三角剪切变形理论研究了受抛物线荷载作用的各向同性固定梁. 文献[6]提出了一种新的无网格局部Petrov-Galerkin(MLPG)方法, 利用一种新的测试函数来解决二维悬臂梁问题. 由于悬臂梁多样的荷载条件和复杂的边界条件, 直接求解其解析解存在一定的困难. 因此, 寻找一种有效的数值方法来解决此类问题十分必要. 虚拟元方法[7]可以看作是有限元方法对一般多边形或多面体单元的扩展, 网格处理比较灵活, 虚拟元空间添加了合适的非多项式函数, 在计算刚度矩阵时, 不需要实际计算这些非多项式函数, 而只需使用自由度.虚拟元空间的引入，便于处理复杂的单元几何和高阶连续性条件, 有效地解决更多的实际问题.

1 悬臂梁方程

考虑四阶边值问题

(1)

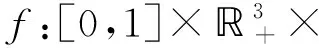
为了求解问题(1), 对于u∈C4[0,1], 假设φ(x)=f(x,u(x),u′(x),u″(x),u‴(x)),

令v(x)=u″(x), 通过变量代换, 问题(1)可转化成两个二阶问题[8]：

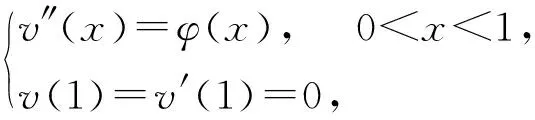
(2)

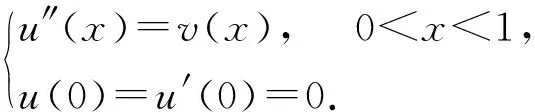
(3)

问题(1)描述了左端固定右端自由的弹性梁的挠度.在力学中, 此问题称为悬臂梁方程.要解决问题(1), 只需求解问题(2)和问题(3).

2 虚拟元方法

2.1 连续性问题与变分形式

为了研究问题(2)和问题(3),首先考虑二维的泊松方程：

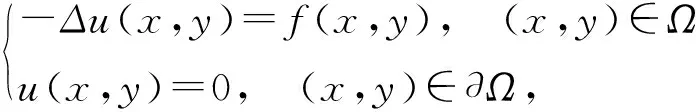
(4)

其中,Ω是2上的一个多边形区域, 且f(x,y)∈L2(Ω).方程(4)的变分形式为:找到使得

a(u,v)=(f,v), ∀v∈V.

(5)

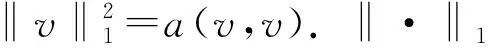
2.2 构造虚拟元空间

首先, 对区域Ω进行剖分.设{Γh}h是将Ω分解为元素K的序列, 设εh为Γh的边的集合,h表示Γh中元素的最大直径.对于Γh内的每个多边形K,xK为K的重心,hK为K的直径.当k≥1时, 定义空间Βk(∂K)为

Βk(∂K):={v∈C0(∂K):v|e∈Pk(e) ∀e⊂∂K}.

其中,∂K表示多边形K的边的集合, 其中，Pk(e)表示次数不超过k的多项式.定义局部虚拟元空间为

Vk(K)={v∈H1(k):v|∂K∈Βk(∂K),Δv∈Pk-2},

且P-1(K)={0}.定义全局虚拟元空间为

Vh={v∈H1(Ω):∀K∈Γhv|∂K∈Βk(∂K),Δv|k∈Pk-2}.

在虚拟元方法中, 自由度对形函数的计算至关重要, 因此, 给出自由度的计算方法.空间Vk(K)的函数仅仅由以下自由度决定:①vh在顶点处的值; ②对于k>1,vh在每条边e上的值; ③对于k>1, 在每个单元上:

其中,

为了方便对双线性形式进行局部离散, 引入下列投影算子.

定义投影算子Π∇:Vk(K)→Pk(K),对于所有的vh∈Vk(K), 都满足下列正交性条件(∇pk,∇(Π∇vh-vh))0,K=0, ∀pk∈Pk(K).

定义L2投影算子Π0:Vk(K)→Pk(K), 对于所有的vh∈Vk(K), 都有(pk,Π0vh-vh)0,K=0, ∀pk∈Pk(K).

当k=1或k=2时, 显然有Π∇=Π0.通过构造与问题的双线性形式有关的投影算子, 可以方便离散双线性形式以及计算刚度矩阵.

2.3 虚拟元离散

基于上述空间和投影算子的定义, 下面将双线性形式进行局部离散.

局部离散双线性形式为

aK(u,v)=aK(Π∇u,Π∇v)+aK(u-Π∇u,v-Π∇v) ∀u,v∈VK,k.

选取φ1,…,φNdof为标准基, 则dofi(φj)=δij,i,j=1,2,…,Ndof.

局部刚度矩阵为

其中,

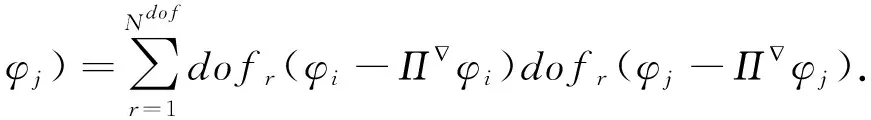
上述的局部离散双线性形式, 具有以下两个重要性质.

引理1[9]对于任意的多边形K∈Γh, 都有

(1)一致性:对于∀vh∈Vh|K, 并且∀p∈Pk(K), 有

(2)稳定性:存在不依赖h和K的常数α*和α*, 使得对∀vh∈Vh|K, 有

综上, 得到离散方程:找到uh∈Vh, 使得

ah(uh,vh)=〈fh,vh〉, ∀vh∈Vh.

(6)

由一致性与稳定性易证式(6)有且仅有唯一解uh.

2.4 误差分析

基于上述离散方程, 根据文献[7], 可得数值解的收敛性.下面对H1范数和L2范数下数值解的误差估计进行讨论.

定理1对充分小的h, 问题(6)有唯一解u∈Vh,H1范数下的误差估计为

‖u-uh‖1≤Chk(‖u‖k+1+|f|k),

其中,C是一个与h无关的正常数.

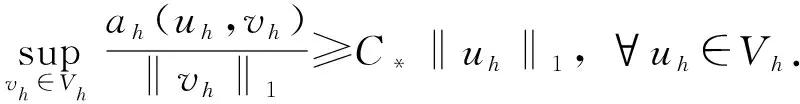
(7)

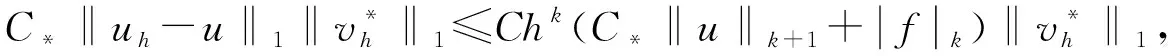
定理2对充分小的h,L2范数下的误差估计如下:

‖u-uh‖0≤Chk+1(‖u‖k+1+|f|k),

其中,C是一个与h无关的正常数.

因为

a(u-uh,ψ-ψI)≤Chk+1‖u‖k+1‖u-uh‖0,

因此,‖u-uh‖0≤Chk+1(‖u‖k+1+|f|k), 结论得证.

3 数值实验

本节通过对端部受抛物线荷载作用的悬臂梁进行数值模拟, 验证了上述理论分析的准确性.对于上述悬臂梁, 文献[11]给出了位移场的精确解.应用虚拟元方法求解, 首先对网格进行剖分, 网格生成的具体步骤参考文献[12].这里选择的剖分区域为Ω=[0,8]×[-2,2].图1给出了网格剖分数N分别为50, 100, 200, 400, 800, 1 600的剖分图.

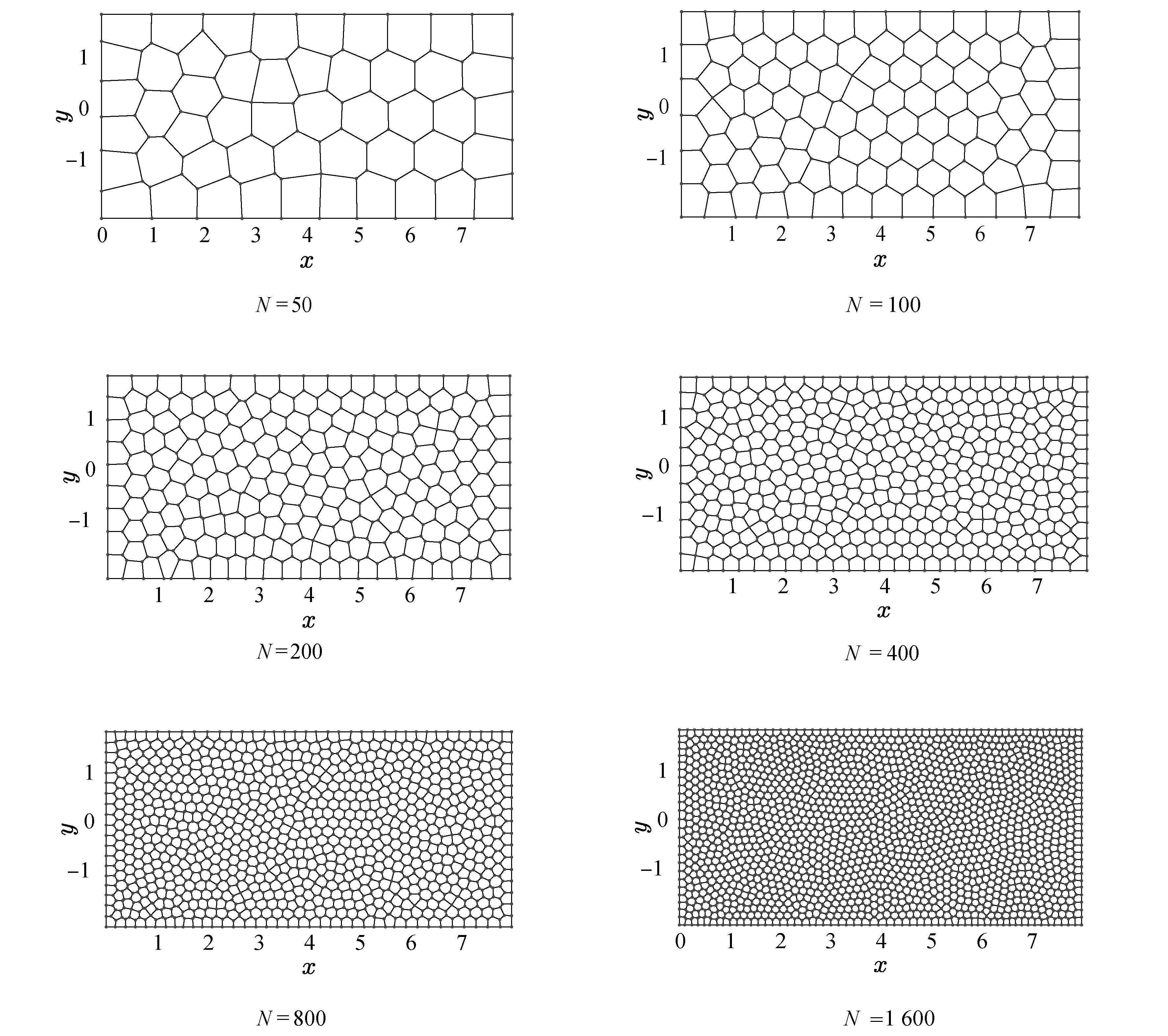
图1 不同网格数对应的剖分图Fig.1 The division diagram corresponding to different mesh numbers

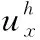
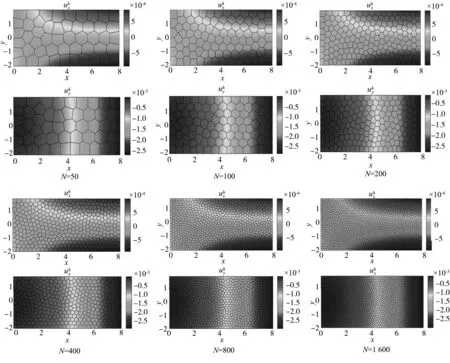
图2 不同网格数对应的数值解Fig.2 Numerical solutions corresponding to different mesh numbers

下面讨论不同范数意义下的相对误差与绝对误差.

表1给出了不同网格下数值解的误差, 其中, Err(L2)和err(L2)分别表示L2范数下的绝对误差与相对误差, Err(H1)和err(H1)分别表示H1范数下的绝对误差与相对误差.

表1 不同网格数对应的相对误差与绝对误差Table 1 Relative error and absolute error corresponding to different mesh number

由表格知, 变化网格剖分个数N=50, 100, 200, 400, 800, 1 600,L2范数下的相对误差和H1范数下的相对误差呈现明显收敛的趋势,L2范数下的绝对误差和H1范数下的绝对误差更加精确, 从而验证了虚拟元离散格式的收敛性与有效性.