直井缝内暂堵转向压裂分支缝起裂方向研究

胡智凡,王贤君,王晓娟,王 维,陈希迪

(1.中国石油大庆油田有限责任公司采油工程研究院，黑龙江大庆 163453；2.黑龙江省油气藏增产增注重点实验室,黑龙江大庆 163453；3.中国石油大庆油田有限责任公司第三采油厂，黑龙江大庆 163000)

暂堵转向压裂技术在国内部分油田成功实施，增产效果显著。直井单层内暂堵转向压裂工艺包含炮眼暂堵、缝口暂堵以及缝内暂堵三种工艺[1-9]。炮眼暂堵、缝口暂堵工艺目的是在压裂层的近井筒形成分支缝，分支缝起裂方向、形成条件已有相关研究成果[10-11]；缝内暂堵工艺目的是在主裂缝两侧形成分支缝，分支缝起裂点位置、形成条件已有相关研究成果[12]，但分支缝起裂方向研究未见相关报道。目前的缝内暂堵转向压裂分支缝形成条件相关研究是假设分支缝与主裂缝垂直，这与实际不符，导致研究结果失真，影响现场诊断、施工控制及压裂效果。本文以多孔介质流固耦合理论为依据，建立缝内暂堵转向压裂分支缝形成有限元模型，分析不同水平应力差对分支缝起裂方向的影响，建立分支缝与主裂缝夹角的定量计算数值模型，并用现场井下微地震监测进行了验证。

1 多孔介质流固耦合理论模型

多孔介质流固耦合理论模型包括基于单向流渗流方程的渗流场、线弹性本构方程的变形场、渗流与变形耦合场三部分[13]。

渗流场方程：

(1)

变形场平衡方程为：

(2)

刘建军等通过实验的方法得出低渗透储层渗透率可以表示为：

K=αe-bσ

(3)

式中：K为储层渗透率，μm2；μ为油相黏度，Pa·s；Ct为综合压缩系数，1/Pa；P为油相压力，Pa；εV为体积应变；t为时间，s；σij为应力分量，Pa；Xij为位置坐标，m；α为Biot系数；Xi为位置坐标，m；fi为体积分量，N；a为实验拟合敏感性系数，10-3μm2；b为实验拟合敏感性系数；σ为有效应力,MPa。

上述方程联立构成流固耦合的基本控制方程,在相应边界条件以及初始条件下,构成多孔介质流固耦合理论模型。基于上述多孔介质流固耦合模型，利用有限元软件，建立多分支缝水力压裂有限元模型。

2 缝内暂堵转向压裂分支缝形成过程有限元模拟

选择流固耦合场，地层弹性模量取45 GP，泊松比0.25，最大水平主应力30 MPa，最小水平主应力27 MPa，液柱压力35 MPa，建立暂堵前主裂缝压裂有限元模型，计算结果如图1所示。

图1 暂堵前最大水平主应力矢量图

从图1可以看出，主裂缝形成过程中(缝内暂堵前)，最大水平主应力方向呈东西向。根据水力压裂经典理论及实验结论[8-11]，裂缝沿最大水平主应力起裂方向起裂，主裂缝沿东西向起裂延伸。

设置主裂缝端部岩石强度无限大，以此来模拟缝内暂堵，按照模拟方案(表1)建立有限元模型，并进行计算分析，结果如图2所示。

表1 模拟方案

模拟结果显示，缝内暂堵后主裂缝两侧最大水平主应力发生偏转，即分支缝起裂方向发生偏转，分支缝与主裂缝并不垂直，二者存在一个小于90°的夹角，水平应力差越小夹角越大，分支缝压裂效果越好。

3 分支缝与主裂缝夹角定量计算数值模型建立

根据分支缝形成过程有限元模拟结果可知，水平应力差为2.0 MPa时夹角为80.0°，水平应力差为3.0 MPa时夹角为65.0°，水平应力差为4.0 MPa时夹角为45.0°，水平应力差为5.0 MPa时夹角为25.0°(图3)。通过线性回归，可得到分支缝与主裂缝夹角和水平应力差的定量计算数值模型：

图2 暂堵后最大水平主应力矢量图

图3 分支缝与主裂缝夹角和水平应力差线性回归

y=-1.25x2-9.75x+104.75

(4)

式中：y为分支缝与主裂缝夹角，°；x为水平应力差，MPa。

4 模型验证

A、B两口井水平应力差分别为2.1 MPa、3.9 MPa，根据分支缝与主裂缝夹角定量计算数值模型，A、B两口井分支缝与主裂缝夹角分别为78.8°和47.7°；根据井下微地震监测解释，A、B两口井分支缝与主裂缝夹角平均值分别72.6°和43.8°，精度达90%以上(图4～7)。

图4 A井缝内暂堵前裂缝形态监测

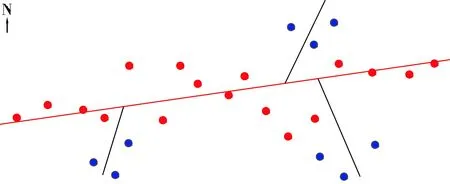
图5 A井缝内暂堵后裂缝形态监测

图6 B井缝内暂堵前裂缝形态监测

图7 B井缝内暂堵后裂缝形态监测

5 结论

(1)应用井下微地震监测结果对分支缝与主裂缝夹角定量计算数值模型的准确性进行了验证，可用来预测分支缝与主裂缝夹角。

(2)分支缝与主裂缝并不垂直，二者存在一个小于90°的夹角，水平应力差越小夹角越大，分支缝压裂效果越好。