FMCW毫米波雷达检测车辆目标跟踪方法

陈凌子，王华伟，刘海青，吕少岚

（1.南京航空航天大学 民航学院，江苏 南京 211106；2.山东科技大学 交通学院，山东 青岛 266590）

0 引言

高分辨率的车辆轨迹数据能够为车辆碰撞预测、交通流参数估计、异常事故感知、违章驾驶行为判别、驾驶员行为分析、驾驶员辅助系统开发等应用提供基础支持。连续、准确、实时的车辆目标跟踪技术是获取车辆轨迹数据的有效手段。车辆目标跟踪技术可划分为单目标跟踪和多目标跟踪两种，相较于单目标跟踪，多目标轨迹跟踪技术处理密集车流时效率更高。近年来，随着城市建设智能化、集约化水平的不断提升，复杂交通环境下的车辆轨迹数据获取问题将更加依赖于多目标轨迹跟踪技术的发展。因此，从长远来看，多目标轨迹跟踪技术的研究对于发挥车辆轨迹数据实用价值和推动未来智能交通系统的发展具有重要意义。

国内外学者对多目标轨迹跟踪算法进行了相关研究，但在复杂交通场景中实际运行时仍存在表现不佳的问题。多目标跟踪的任务是将传感器对每个目标采样得到的量测数据分别关联至不同轨迹，对各条轨迹进行平滑和预测，然后估计下一时刻的目标状态，其主要工作包括航迹的起始、维持和消除等[1]。目前应用较广泛的目标跟踪算法主要有卡尔曼滤波算法[2]、聚类算法[3-4]和数据关联算法[5]。卡尔曼滤波器本质上是一种线性滤波器，无法对极坐标系下的雷达目标进行有效跟踪。因此，出现了一些非线性滤波跟踪算法[6]，如扩展卡尔曼滤波、自适应扩展卡尔曼滤波[7]、自适应Sage-Husa 卡尔曼滤波[8]。基于数据关联的目标跟踪算法主要内容包括关联门形成、点迹关联、跟踪起始、跟踪维持与跟踪结束等多个方面。比较经典的数据关联算法有最近邻数据关联（Nearest Neighbor Data Association,NNDA）[9]、概率数据关联（Probabilistic Data Association,PDA）[10]、联合概率数据关联（Joint Probabilistic Data Association,JPDA）[11]及多假设跟踪（Multiple Hypothesis Tracking,MHT）[12]。但传统的数据关联算法在实现目标跟踪时存在一个共性问题：目标稀疏时效果良好，但目标密集时表现较差[13]。针对此问题，Chen等[14]提出了一种在密集杂波环境下使用组合交互式多模型概率数据关联算法跟踪机动目标的改进算法，能在一定程度上降低杂波和背景噪声的影响，但算法本身没有考虑车辆目标的运动规律，在复杂交通场景下运行时仍可能出现轨迹漂移、中断、缩短等异常情况。近年来，调频连续波（Frequency Modulated Continuous Wave,FMCW）毫米波雷达检测技术因同时具有抗干扰能力强、测速精度高、分辨率高、可全天候全天时工作的特点而在交通监管领域得到广泛应用，如实时速度控制、交通监测[15]和自动驾驶等方面。该技术可获取目标的距离、速度、角度及散射面积值等信息[16]，即高分辨率、高精度的车辆点迹数据。不过，目前毫米波雷达数据的应用大多只停留在多目标检测识别层面，而缺乏深层次的挖掘与分析。若利用FMCW 毫米波雷达数据实现交通场景下多车辆目标跟踪，将在发挥数据潜在价值的同时提升车辆轨迹跟踪效果。

为解决复杂交通场景下多目标轨迹跟踪异常问题、提高目标识别和轨迹跟踪精度，本文将基于FMCW 毫米波雷达交通数据，提出一种设置了矩形跟踪门和关联准则的改进最近邻点迹关联算法，通过产生点迹关联对实现轨迹状态更新。然后，对于提取到的有效车辆轨迹，采用三阶贝塞尔曲线算法进行平滑处理，以实现异常点迹的位置纠偏和缺失帧的位置补偿。最后，利用实际样本数据对上述方法进行验证。

1 研究方法与数据获取

1.1 研究方法

本文所设计的多目标轨迹跟踪方法流程如图1所示。

该方法具体分为以下3个步骤：

步骤1：原始数据预处理。初步剔除噪声和杂波点，并进行参数转换。

步骤2：基于轨迹状态管理实现车辆目标轨迹提取。轨迹状态包括轨迹起始、轨迹维持和轨迹结束。对于处于起始和维持状态的轨迹，基于改进最近邻点迹关联算法实现其状态更新。

步骤3：基于三阶贝塞尔曲线算法实现车辆目标轨迹平滑。对步骤2 提取的车辆目标原始轨迹做滑窗式平滑处理。

1.2 数据获取

本文旨在解决复杂交通场景下FMCW 毫米波雷达多目标轨迹跟踪问题。为收集样本数据，本研究在青岛市李沧区黑龙江中路进行了试验。试验路段东侧建有万达商场，车流密集，符合设定的复杂交通场景的要求，同时有过街天桥横跨该路段，满足为减少目标遮挡而设计的将毫米波雷达数据采集系统安装在道路上方的要求。FMCW毫米波雷达目标检测结构主要包括：1 个独立e200z7260核和1个e200z420核的NXP-MPC5775K 32 位异构多核微控制器、1 个NXP-MR2001 射频前端和2 组发射、4 组接收的平面微带阵列天线。各项技术参数如表1所示。

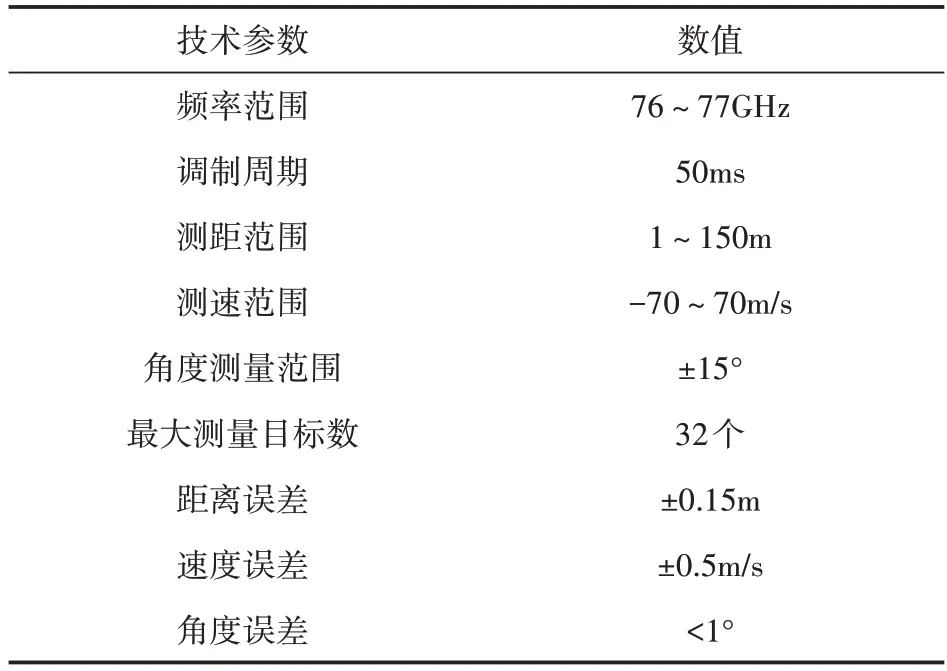
表1 FMCW毫米波雷达的技术参数

原始数据中包含目标运动状态的4 个参数分别定义为：

（1）距离（rm）：目标与雷达之间的径向距离。

（2）速度（vm/s）：目标与雷达的径向相对速度。

（3）角度α（°）：目标与雷达垂直探测方向的水平夹角。

（4）RCS（Rada Cross Section）值（dB）：表征目标在雷达波照射下所产生的回波强度。

图2形象地描绘了参数r,v,α的具体含义：

图2 中，雷达安装在A点，H为安装高度，θ为安装俯仰角。以雷达的竖直投影点O为原点，雷达所在竖直方向为z轴，雷达垂直探测方向（射线AP）的水平投影为y轴，建立空间直角坐标系。点C处为探测目标，点O至点C的距离为LOC，点A至点C的距离LAC为参数r，∠COP为参数α，目标实际运动速度为vs，vs在线段AC方向上的正交分量为参数v。OC为AC的竖直投影，故在实际实验中，雷达安装高度H为3.5m，有效目标径向距离LAC约在15～80m 范围内，令LOC≈LAC，则LOC的取值误差在0.077～0.414m 范围内。而在产生点迹关联对时，距离增量误差取值均大于LOC取值的最大误差，因此，为简化计算，本文取LOC≈LAC，即LOC≈r。

2 FMCW 毫米波雷达多目标轨迹跟踪方法

2.1 FMCW毫米波雷达数据预处理

2.1.1 噪声剔除

原始数据中存在一系列由金属护栏、灯柱等引起的背景噪声，此类噪声具有距离在一定范围内变化而速度保持为0 的特点。由于本次数据采集过程中未观测到停靠车辆，且FMCW 毫米波雷达可检测到低速运动的目标，所以将原始数据中速度为0 的目标均视为背景噪声并剔除。然后，为便于区分量测目标，在每帧数据的第2 列位置新增1列，对速度不为0的目标依次编号，并去除参数全为0的占位目标。处理后的数据格式如表2所示。

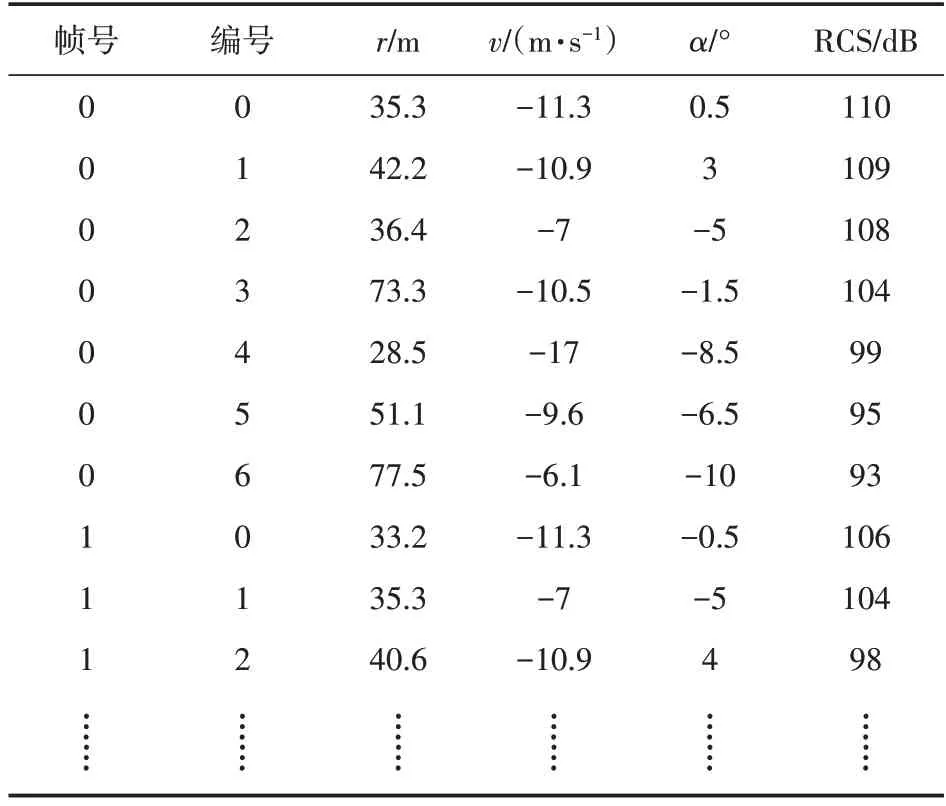
表2 噪声剔除后每帧数据格式

若第m帧数据包含n个量测，可将此帧数据表示为A(m,n)=(a1,a2,…,an)T，其中第i个量测表示为

2.1.2 参数转换

在后续矩形跟踪门的研究中，将图2 所示空间直角坐标系转换为图3 所示平面直角坐标系，以便于对距离、速度等的差值计算。将目标C在图2 空间坐标系中的运动参数r,v转换至图3 平面坐标系的计算公式见式（1）。

图3 和式（1）中：rx,ry分别为目标C在图3平面直角坐标系中的横、纵坐标；vs为目标实际运动速度。

2.2 基于轨迹状态管理的车辆目标轨迹提取方法

2.2.1 车辆轨迹状态管理方法

由于环境复杂、车流量大，每帧数据包含多条车辆轨迹，且掺杂着未被剔除的虚假目标，其中虚假目标存在的时间短且一般不呈现距离随时间连续变化的特点。因此，本文利用轨迹状态管理方法提取有效车辆轨迹，具体流程如图4所示。

图4中，轨迹状态包括3种：

（1）轨迹起始：新目标连续出现2 帧，轨迹跟踪开始。

（2）轨迹维持：某条轨迹自跟踪起始后，每连续M帧至少更新1次。

（3）轨迹结束：某条轨迹连续M帧未更新。

判别为结束状态的轨迹，若其关联长度不小于L帧，则该条轨迹为有效车辆轨迹。

2.2.2 改进最近邻点迹关联算法

点迹关联对的定义为：2 个有时间间隔的目标量测形成的关联。传统最近邻数据关联算法基于统计距离最近原则将点迹与目标轨迹关联，但在车流量大、杂波点较多的情况下，容易导致轨迹异常中断、轨迹漂移、轨迹缩短等异常情况发生。其中，轨迹异常中断指1个目标的整条长轨迹被跟踪为两部分，即识别为2个目标；轨迹漂移指当2个速度相近的目标先后出现在道路相同位置时，由于出现较早的目标其轨迹未被判别为结束，仍在不断外推，而出现较晚的目标的轨迹后半段被关联至出现较早目标的轨迹尾部；轨迹缩短指提取到的轨迹的有效长度远小于该目标在探测范围内真正出现的帧数，缺失帧多是杂波和虚警复杂的帧次。上述3种常见的异常情况如下页图5所示。

为尽量避免上述异常情况的发生，本文基于传统最近邻数据关联算法，考虑到车辆目标运动规律，提出一种设置了矩形跟踪门和关联准则的改进最近邻点迹关联算法：通过矩形跟踪门产生初步点迹关联对，通过关联准则产生最终点迹关联对，其基本流程如下页图6所示。

当2 个时间间隔为t的量测=(r1,v1,α1)和形成初步关联时，2 个量测在时间t内的距离增量和速度增量应满足基本运动规律，即各增量小于最大增量值，如式（2）～式（4）所示：

式（2）～式（4）中：Δx,Δy和Δv分别为横向距离增量、纵向距离增量和速度增量；Rx,Ry分别为横向距离误差和纵向距离误差，根据车辆平均尺寸和雷达距离探测的系统误差设定；Rv为速度增量阈值，根据雷达分辨率和车辆最大加速度设定。

如图7 所示，假设点迹1 在时间t内做匀速运动，则经过时间t后应出现在外推点（圈点4）位置，以外推点为中心设置矩形跟踪门，当门内有点迹（点迹2和点迹3）存在且该点迹相对于点迹1的速度增量小于速度增量阈值时，点迹1分别与门内点迹形成初步关联对。图7 中的初步关联对为1-2和1-3。

设定关联准则的目的是解决初步关联对中一对多和多对一的问题。在分别记录上一时刻被更新轨迹和上一时刻未更新轨迹的尾部量测后，关联准则具体表述为：

（1）若尾部量测无对应初步关联对，则当前时刻该条轨迹不更新。

（2）若尾部量测对应1 个初步关联对，则该初步关联对成为最终关联对，当前时刻该条轨迹完成更新。

（3）若尾部量测对应多个初步关联对，则按照最近邻原则选取最终关联对，当前时刻该条轨迹完成更新。

（4）若存在多个尾部量测对应当前帧的同一点迹，则根据雷达探测的车流方向进行筛选：车流朝向雷达安装位置时，去掉当前帧量测径向距离大于尾部量测径向距离的关联对；车流背向安装位置时，去掉当前帧量测径向距离小于尾部量测径向距离的关联对；处理后，若当前帧点迹只对应1 个尾部量测，则选为最终关联对，若仍对应多个尾部量测，选择的最终关联对应保证当前最长在跟踪轨迹得以更新。

轨迹状态更新的原则是优先更新上一时刻被更新轨迹，然后更新上一时刻未更新轨迹，最后考虑是否存在新增轨迹，具体流程如图8所示。

由于1 个量测不能被重复关联至轨迹尾部，故图8 中某时刻剩余量测应是某时刻全部量测减去因轨迹状态更新而被占用的所有量测。

2.3 基于贝塞尔曲线的车辆目标轨迹平滑方法

2.3.1 三阶贝塞尔曲线算法

贝塞尔曲线是样条曲线中的一种，能够实现直线段之间的平滑过渡[17]。如图9 所示，三阶贝塞尔曲线有4 个控制点P0,P1,P2,P3，当各连线的长度满足式（5）时，点P0123的轨迹构成三阶贝塞尔曲线。式（5）中，P0P01表示点P0与点P01之间的欧氏距离，P0P1,P1P12,P1P2,P2P23,P2P3,P01P012,P01P12,P12P123,P12P23,P012P0123,P012P123同理。p时刻（0≤p≤1）某点Pp在曲线上的位置B(p)由式（6）计算可得。

2.3.2 滑窗式轨迹平滑方法

对于提取到的有效车辆轨迹，采用三阶贝塞尔曲线算法做滑窗式平滑处理，如图10所示。前4 个量测处理完毕后，释放起始点，利用平滑后的第2、第3 点与第4、第5 原始点再次进行平滑处理，即滑窗式处理。

3 实例应用

3.1 数据预处理

试验采集的原始样本数据中，前250 帧各目标径向距离信息如图11所示，可初步看出，距离保持不变的水平线为需要剔除的一部分噪声和杂波，距离连续变化的倾斜线为需要跟踪的车辆轨迹。经噪声剔除后，前250 帧数据中各目标的径向距离信息如图12所示。

3.2 车辆轨迹提取

判断轨迹结束的依据是该条轨迹连续13帧未更新，即取M=13。13 帧是车速较快的车辆从驶入到驶出雷达探测盲区所需的时间：车速取值85km/h（取速度大于等于70km/h的目标的速度平均值），雷达探测盲区为径向距离0～15m。若将M扩大取值，可能导致2 条轨迹连为1 条的异常情况发生。

当关联长度不小于20帧时，判断该条轨迹为有效车辆轨迹，即取L=20。在使用FMCW 毫米波雷达探测车辆目标时，还安装了摄像机记录实时同步视频，使轨迹提取效果评价有据可依。在对应前12.5s 的同步视频中，观察到出现在探测区域内的车辆总数为13 辆（观察数）。前250 帧原始数据在不同L取值下的轨迹提取结果如表3 所示，可以看出，当L为20～23 帧时，轨迹提取效果最好。

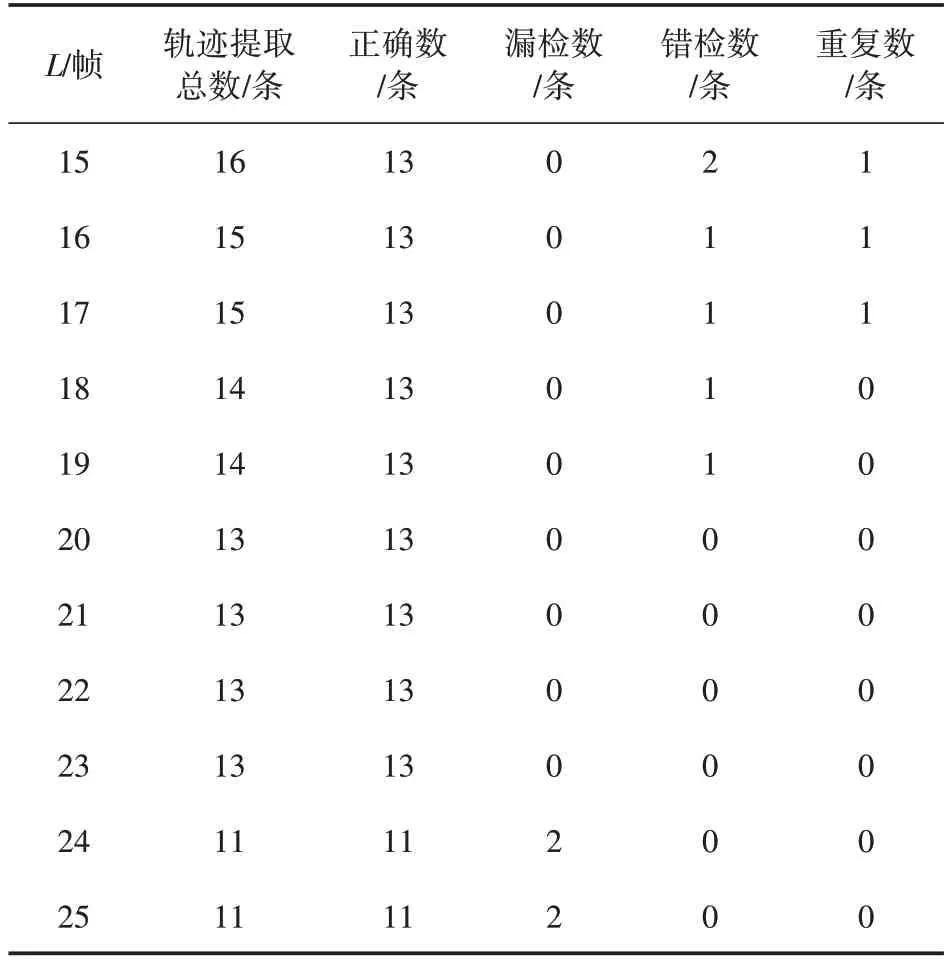
表3 不同关联长度下前250帧原始数据轨迹提取结果

为进一步观察L取值对轨迹提取效果的影响，在前750 帧（37.5s）的视频中，共观察到48 辆（观察数）车辆，然后在前750帧原始数据中提取有效车辆轨迹。不同L取值下轨迹提取结果如图13 所示，其中：正确率=正确数/轨迹提取总数，漏检率=漏检数/观察数，错检率=错检数/轨迹提取总数，重复率=重复数/正确数。

从图13 可以看出，在L=25 时，正确率虽比L=20时高，但其漏检率也随之增高。可见，当关联长度L=20时，正确率较高，错误率、漏检率和重复率均较低，综合提取效果最好。在M=13,L=20 的情况下，所提取的前250 帧原始数据中的13条有效车辆轨迹如图14所示。

将图14 与图12 进行比较，如图15 所示，可以看出：

（1）有效车辆轨迹的径向距离集中在10～80m 范围内，而0～10m 和80～140m 范围内的点迹几乎全部被剔除。即只有少数车辆在距离雷达磁波发射点80m 以外的区域开始被探测，或在距离雷达磁波发射点10m 以内的区域仍可被有效探测。因此，得出以下两点结论：①本文所用毫米波雷达的实际有效探测区域是距离磁波发射点10～80m范围内，若超出该范围，则获取的目标运动参数与实际数值存在较大偏差；②径向距离在0～10m和80～140m范围内的点迹极有可能是杂波或虚警，故可根据径向距离初步判断目标真实性。

（2）所提取的有效车辆轨迹的长度小于该目标实际被探测的帧数。该目标的某些点迹未被关联的原因在于：①该点迹在雷达有效探测区域以外，速度值不准确，无法被有效识别；②该点迹在雷达有效探测区域内，但其与该目标的其他点迹的距离差值、速度差值稍大于系统设置的阈值。

3.3 车辆轨迹平滑

13 条有效车辆轨迹经三阶贝塞尔曲线算法平滑处理后如图16所示。

可以看出：整体上，与图14 的原始轨迹相比，图16的平滑轨迹突出点减少，点迹位置规律变化；局部上，原始轨迹新时刻点迹位置落后于旧时刻点迹位置的异常情况得到较好改善。为定量评价轨迹平滑度的提升效果，提出一种曲线拟合的方法分别计算轨迹平滑处理前后的径向距离误差，如图17～图18所示。

图17（a）所示为1 条车辆原始轨迹，利用四次多项式拟合可得到图17（b）中红色曲线，由式（7）计算原始轨迹与拟合曲线的径向距离误差s1=0.631。然后，如图18（b）所示，将该曲线同位置放在图18（a）所示车辆平滑轨迹中，由式（8）计算平滑轨迹与拟合曲线的径向距离误差s2=0.446。s2＜s1，说明车辆原始轨迹经滑窗式贝塞尔曲线算法处理后平滑度得到改善。13条有效车辆轨迹平滑处理前和平滑处理后的曲线拟合误差汇总如表4 所示，可见13 条原始车辆轨迹经平滑处理后，平均径向距离误差由0.555 降至0.446，总体平滑度得到改善。

表4 13条有效车辆轨迹平滑处理前与处理后曲线拟合误差汇总表

式（7）～式（8）中：ri为原始点迹的径向距离；为对应时刻拟合曲线上的径向距离；为平滑点迹的径向距离。

4 结论

为有效获取复杂交通场景下的高分辨率车辆轨迹数据，本文提出了一种多目标车辆轨迹跟踪方法，并利用FMCW 毫米波雷达采集的真实数据验证了算法的有效性。研究结果表明：

（1）设置了矩形跟踪门和关联准则的改进最近邻点迹关联算法能够有效提高点迹关联准确度，解决了传统最近邻数据关联造成的车辆轨迹漂移、异常中断和长度缩短等问题。

（2）所采用的轨迹状态管理方法能够有效判别和提取车辆轨迹，提高了复杂交通场景下目标识别和轨迹跟踪的准确度。

（3）基于三阶贝塞尔曲线的轨迹平滑处理在一定程度上降低了原始数据的测量误差，并实现了缺失帧补偿。

当道路上有大型车辆出现时，如货车等厢型车辆，由于其车身较长，雷达探测信号可能在车身的不同位置发生反射，使得同一帧数据中出现同一辆车的多个量测。但本文在轨迹状态更新时只关联1 个目标的1 个新量测，在以后的研究中，将合并同帧数据的同车量测，折中确定大型车辆的位置。