基于贝叶斯网络的地铁设备故障诊断方法

李松峰，宋震，侯珏，肇北，王江涛，刘书浩，宋晓敏

（1.交通运输部科学研究院，北京 100029；2.城市轨道交通运营安全管理技术及装备交通运输行业研发中心，北京 100029；3.京东数智工业科技有限公司，北京 100176；4.北京京港地铁有限公司，北京 100068）

0 引言

随着各地地铁运营里程持续快速增长，因系统设备故障影响路网运行秩序、服务质量甚至运营安全的事件时有发生[1]。目前，设备故障诊断高度依赖检修人员经验，无法适应地铁智能化、智慧化的发展需求[2]。同时，当前地铁设备呈现出复杂化和多样化特征，不同设备的故障诊断方法不同，仅依靠检修人员经验已无法有效应对。因此，行业迫切需要智能化的故障分析诊断手段，有效进行故障和系统可靠性分析，提升地铁运营安全保障能力。

既有的国内外研究大多是对可能造成故障的因素进行分析，然后通过测算其相关概率来进行故障排查，如赵奕等[3]基于故障树原理，对故障影响因素进行了定性和定量分析。故障树分析法是地铁故障常用的分析方法，但其仅适用于故障分类较简单且依赖关系较明确情况下的故障分析，同时不能进行逆向故障诊断。为了让故障分析更贴近实际，一般在因素之间增加概率描述。王宇等[4]引入主元分析法对检修数据进行预处理，在此基础上建立概率神经网络模型，将主元分析与概率神经网络相结合进行故障诊断。但该方法在进行数据预处理时，可能会失去原来有效的数据信息，影响模型精度。针对故障间逻辑关系相对明确或故障分类相对清晰的情况，可采用故障树转贝叶斯网络的方法来识别系统中的薄弱环节，进而诊断故障，这种方法在众多领域得到了应用。Zhang等[5]采用贝叶斯网络评估了核电厂的运营状态，对多个影响操作者状态的因素进行综合分析，扩展了贝叶斯网络的应用维度。周巧莲等[6]基于地铁车门系统的故障树，利用贝叶斯网络进行了可靠性分析并获得了系统的关键环节，该方法可为维修策略提供技术支持，但可靠性分析指标较单一，未能全面反映系统的可靠性。崔袁丁等[7]通过贝叶斯网络特有的概率计算方法，对铁路旅客服务质量评价体系进行逐级计算，使得评价过程更具条理。Zhang等[8]将模糊理论引入贝叶斯网络模型，以地铁隧道渗漏事故为例，验证了该方法可有效克服现有概率估计方法的局限。李兴运等[9]将模糊贝叶斯网络结合证据理论分析法，对多态受电弓系统进行可靠性分析，增强了贝叶斯网络处理不确定认知的能力。Zarei等[10]用故障模式影响分析法分析了城市天然气管道运输风险，用贝叶斯网络进行建模并评估，成功解析出故障主要影响因素，使风险分析更全面。

以上研究均基于贝叶斯网络模型，从概率角度解决了故障分析无法高效定位故障原因的难点问题，对故障关键因素进行了有效辨识和逆向诊断，但对贝叶斯网络的应用局限于基于故障概率的诊断过程，忽视了故障诊断需要的时间成本，也缺少在实际场景下对比人工分析和贝叶斯网络分析效率的研究。鉴于此，本文基于故障发生概率和排查时间提出“预期时间”测度指标，并以地铁客室门设备故障诊断为例，对比基于贝叶斯网络的机器算法与人工故障排查的效率差异，以期为提高地铁设备故障维修效率提供理论支撑。

1 基于贝叶斯网络模型的设备故障分析方法

1.1 建立设备故障的故障树

地铁系统发生故障将直接影响系统可用性，而地铁的可用性通常与系统条件、运行条件和维修条件密切相关[11]。故障分析的价值在于支撑设备发生故障时的快速诊断和处置，以恢复设备的可用性。

故障树分析的基本思想是：将系统最不期望的故障现象作为顶事件，利用演绎推理的方式逐级向下分解，直至所有输入原因事件无法分解为止。但是，该方法无法对系统发生多个相互关联或数量不确定的故障进行快速有效排查。

1.2 建立设备故障贝叶斯网络模型

贝叶斯网络（Bayesian Networks,BN）是基于概率推理的图形化分析方法，一般用于决策分析。贝叶斯网络由贝叶斯网络结构和条件概率两部分组成[12-13]。设一个贝叶斯网络由节点{X1,X2,…,Xn}构成，其中Xn为第n个节点。该贝叶斯网络可表示为BN=＜G,P＞。G表示贝叶斯网络的网络结构图，它是一个有向无环图，图中包含两个要素：节点和有向弧。节点表示系统的随机变量或事件；有向弧是具有映射方向的弧线，它连接节点，从原因事件指向结果事件，表示随机变量或事件间的依赖性或因果关系。P是贝叶斯网络的二维条件概率表（Conditional Probability Table,CPT），它定义节点之间的概率关系，表征不同节点之间的连接关系，根节点（没有任何父节点的节点）概率为其先验概率[14]。

图1 是一个简单的贝叶斯网络示意图，图形中每个节点代表的是相应问题的一个随机变量，节点变量可以是任何变量的抽象。贝叶斯网络能提供更为丰富的关系类型，让决策分析更完善和准确。

本文所指的故障是无法由监测设备提供的信息直接得出的源头故障，而现象是指可直观得到或由监测设备提供的现象。

故障树模型通过逻辑门连接各事件，而贝叶斯网络通过有向边与对应的条件概率分布实现建模，鉴于这种相似性，可将故障树模型转化为贝叶斯网络模型，实现贝叶斯网络建模。转化算法如下[15-16]：

（1）将故障树的每个底事件对应到贝叶斯网络的根节点；

（2）将故障树中各基本事件的先验概率值作为贝叶斯网络中对应根节点的先验概率进行赋值；

（3）将故障树的中间事件和逻辑门分别对应表达为贝叶斯网络中的节点和联系强度，依照故障树模型中各事件间的逻辑关系连接贝叶斯网络的各节点，对相应的节点附加等价的条件概率分布表。

图2 所示为故障树模型中基本逻辑门——“或”门和“与”门——对应贝叶斯网络模型的表达形式。右侧每行的条件概率对应CPT 表格中间的一行。

1.3 基于贝叶斯网络模型的设备故障分析

1.3.1 设备故障概率分析

基于贝叶斯网络可以由故障的先验概率和条件概率进行预测推理，最终确定设备故障发生的原因及相应的概率。因故障树中各底事件相互独立且均为“与”“或”的关系，故也可以确定条件概率[17]。在确定各概率后，基于独立性假设定义，如果事件A1,A2,…,An互不相容，P(B) ＞0时的贝叶斯公式为[18]：

式（1）中：P(Aj)为第j个事件A的先验概率；P(Aj|B)为第j个事件A的后验概率；P(B|Aj)为条件概率。

由贝叶斯公式进行故障诊断，可得出各子节点造成系统故障的概率，然后按照概率大小顺序依次排查不同故障发生的原因，最大限度减少故障导致的损失。贝叶斯网络模型可根据最新的先验概率（如P(A),P(B)）和条件概率（如P(A|B)）进行迭代，不断改进诊断效果。

1.3.2 基于预期时间的故障诊断分析

基于贝叶斯网络的故障诊断通常用于研究系统或设备的可靠性，但一般不对故障排查成本进行分析。而在实际应用中，应优先对故障概率高且排查时间短的故障进行排查，提高故障诊断和解除效能。因此，本文引入预期时间Te。预期时间指排查故障所用时间的数学期望，计算公式如下：

式（2）中：Pf为故障发生的概率，经由贝叶斯网络计算所得；T为故障平均排查时间，由设备特性及维修经验得到。

当故障排查时间相同时，应优先考虑故障概率。当故障概率相同时，应优先考虑排查时间短的故障。本文基于预期时间指标Te，利用Python及PyAgrum框架实现贝叶斯故障排查功能。

2 实例分析

在地铁车辆系统中，客室门设备是机械与电气相结合的复合型装置，是保障行车安全的关键设备。因此，本文以地铁车辆客室门设备为研究对象，对国内17 家地铁运营企业共计190 条车辆客室门设备故障数据进行分析，验证前述模型的有效性。

2.1 建立客室门设备故障树

将客室门设备故障作为顶事件，结合各故障现象及对正线运营场景的影响情况建立故障树模型，根据开门控制逻辑，利用故障树模型对各故障模式进行分析，其各层事件描述和标号见表1，故障树模型图如图3所示。

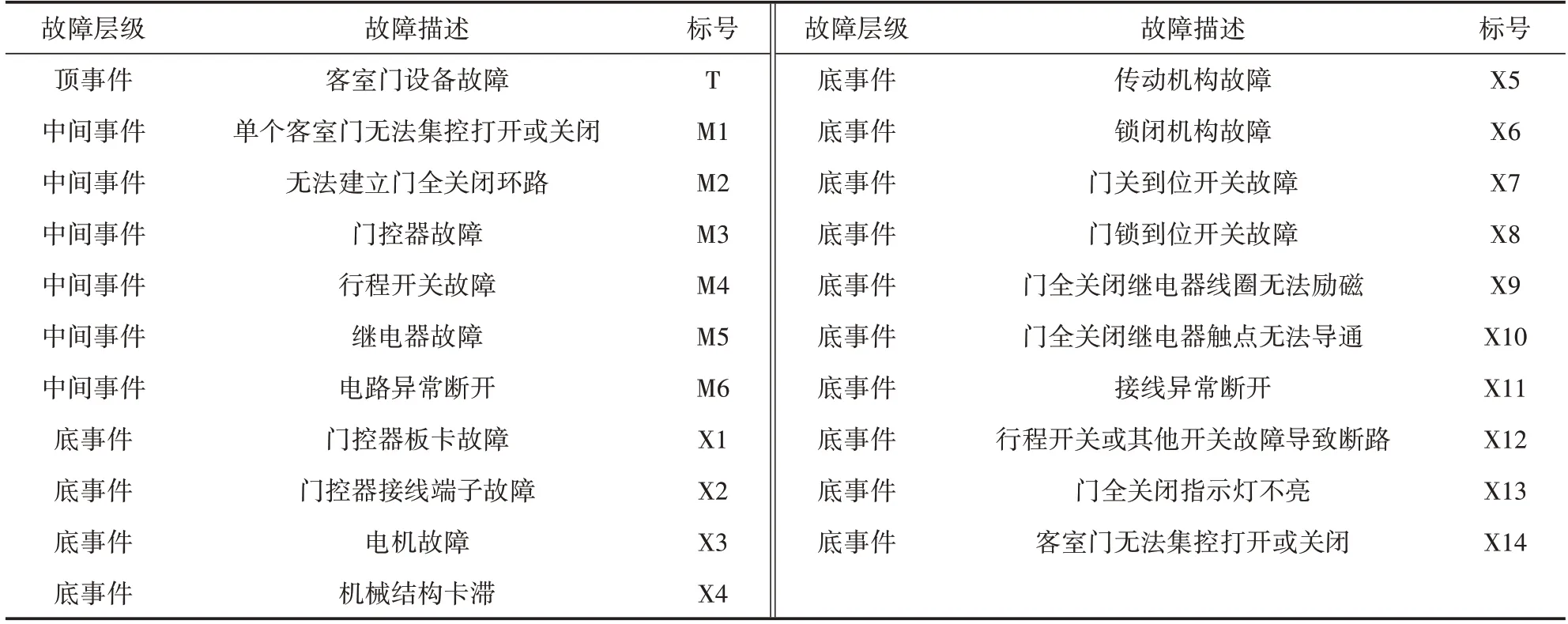
表1 故障树各层事件的描述和标号

2.2 建立客室门设备故障贝叶斯网络模型

根据1.2 节提出的转化原则，可将客室门设备故障的故障树模型转化为贝叶斯网络模型，如图4所示。

同时，根据全国17家地铁公司故障调研数据得到客室门设备各故障模式的先验概率如表2 所示。假设根节点相互独立，由图3 可知各中间事件的条件概率分布只有1（发生故障）和0（无故障）两种。表中排查时间为历史数据的均值。需注意的是，“先验概率”和“排查时间”在现有的维护手册里找不到，但对工人的维修效率有重要影响。

表2 客室门设备各故障模式先验概率表

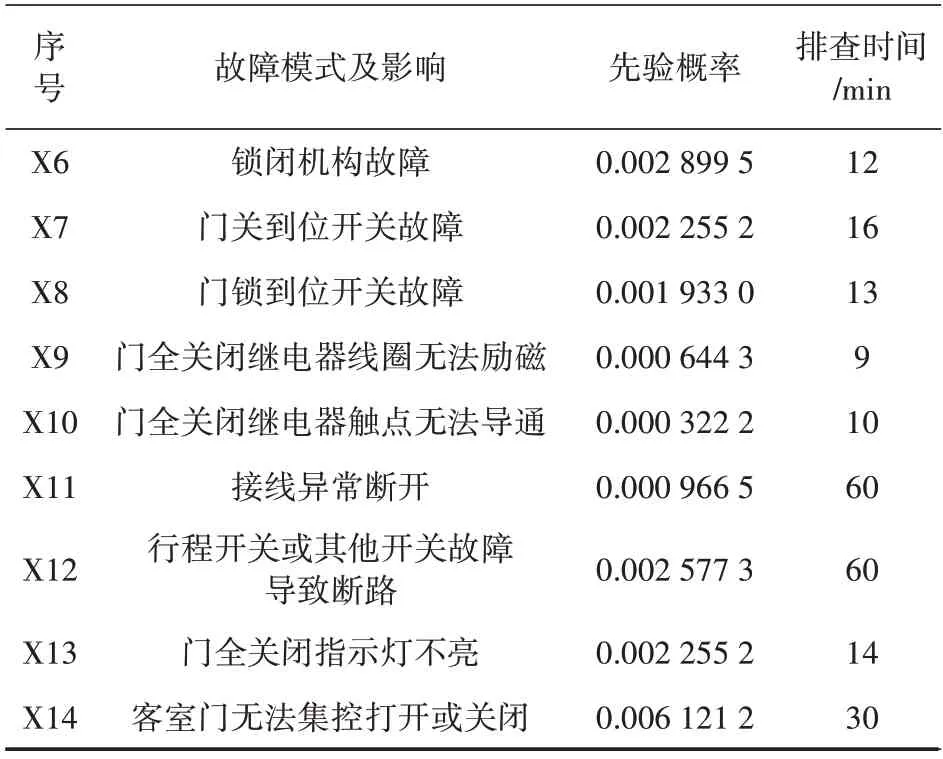
表2 （续）

2.3 客室门设备故障分析

基于表2 数据，利用式（1），通过贝叶斯网络模型可对客室门设备故障概率进行分析。根据式（2）可以得到各故障此时排查的预期时间Te。因此计算得到客室门设备故障时各根节点故障概率及所需要的排查预期时间如表3所示。

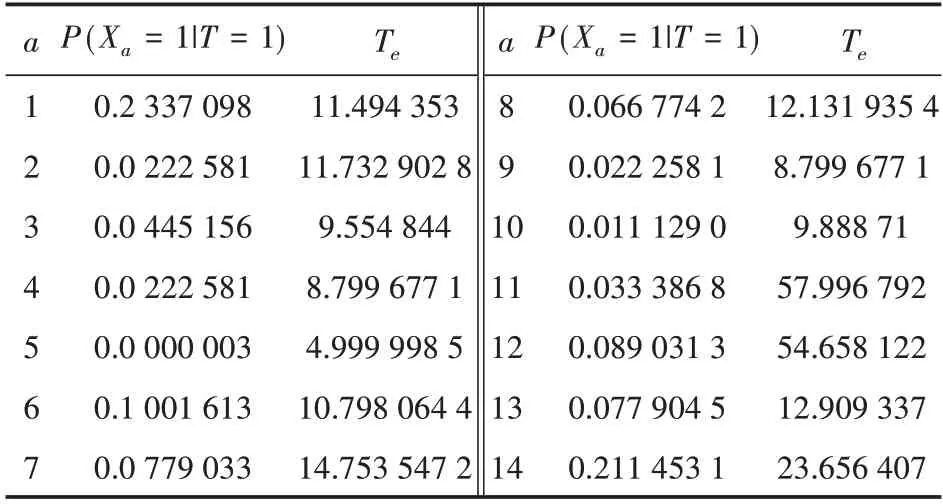
表3 客室门设备故障时各根节点故障概率

从表3 中可看出，当客室门故障时，对比X13“门全关闭指示灯不亮”和X14“客室门无法集控打开或关闭”，X14发生概率更大，不考虑其他因素时，应优先排查X14。但根据式（2），易得Te13＜Te14，在诊断时间最优原则下，此时应先排查X13。因此，当概率和时间都不相同时，预期时间对故障排查的顺序更有指导意义。

2.4 基于预期时间的贝叶斯网络故障诊断

采用基于3D数字孪生的蒙特卡洛仿真系统进行效果验证，先在14个故障点中随机生成一个故障点，假设人工故障诊断时没有任何参考信息，诊断过程完全随机进行，用户点击任意点代表对该故障进行检查，如果点击到有故障的点，则代表故障排除。在基于预期时间的贝叶斯网络故障诊断模式下，用户每次选择算法推荐的第1个故障点，即预期时间指标最小的那个故障，以此类推直到选择到真正的故障点。

表4为人工随机排查故障和应用本文算法（以下称为“机器算法”）进行故障诊断的过程对比。测试中，人工排查共历经10 步发现了故障点X13，耗时188min；而基于预期时间的贝叶斯网络故障诊断算法仅历经2 步，仅耗时19min 就发现了故障点X13，较人工排查节省了169min。图5所示为两种方法诊断用时结果对比。

在上例中，利用机器算法进行故障诊断所用的时间只是人工随机排查的1/10，连续利用算法进行1 000次蒙特卡洛仿真计算，其结果如图6所示。从直方图图6（c）和图6（d）可以看出，随机排查的用时在250min以上的占比最多，其余比较平均分布在0～250min，而在基于预期时间的贝叶斯网络算法模式下，诊断的时间大多小于150min，大于200min的只占很少一部分。

在实际生产场景中，维修工人一般能凭借经验根据故障现象进行故障原因的初步判断。因此，人工故障诊断的过程并不是完全随机的，而是通过制定策略进行有序的排查，这里涉及两种不同的排查策略：第一种是严格按照排查时间长短顺序进行排查，由排查时间最短的故障开始直至找到故障，本文称之为时间排序策略排查；第二种是按照故障树自上而下，对造成顶事件的各中间事件依排查时间顺序进行排除，对每个中间事件中的底事件也依时间顺序进行排查，一个中间事件的底事件全部排查完再进行下一个中间事件的排查，本文称之为综合排序策略排查。对两种人工排查策略下的故障诊断分别进行1 000 次迭代仿真，输出结果的对比如图7和图8所示。

从图7、图8 可以看出，两种策略排查方法的用时都分布在0～250min，时间排序手动排查用时集中在150min左右，而综合排序手动排查用时较多分布在250min左右。

综上，3 种人工排查方法与本文所提算法的故障诊断结果对比如表5 所示，机器算法诊断的平均用时分别是3 种人工排查方法平均用时的48.49%,46.48%和43.72%。虽然机器算法的用时不总是小于人工排查的用时，但是机器算法用时的平均值、中位值及标准差都远小于人工随机排查。在仿真中模仿有经验的维修工人，综合考虑概率和平均排查用时进行故障排查（即有策略的人工排查），相较于此，利用本算法可节省15%～30%的时间。在日常故障维修工作中，设备故障的修复时长在故障处置总时长中占比较小，而故障诊断耗时较长，应用基于贝叶斯网络模型机器算法能快速分析出系统中的薄弱环节，提高地铁设备系统的维修效率。

3 结语

本文将故障树转化为贝叶斯网络模型应用到地铁设备故障分析中，通过引入预期时间指标，基于贝叶斯网络构建了一种新的设备故障诊断算法，并以地铁车辆客室门设备故障为例，通过仿真测试对比人工随机故障排查和基于本文算法的故障诊断用时。根据模型输出结果，基于本文算法进行故障诊断所消耗的时间是人工随机排查时间的43%～48%，相比于有策略的人工排查，机器算法估算可节约15%～30%的时间。由于本文中用于对比的3 种人工故障排查方法均设定了一定的原则，导致故障排查过程存在一定程度的机械性，也没有考虑不同经验、知识背景的维修人员在诊断故障逻辑方面存在的差异，后续研究中可予以加强，以更真实地还原实际生产场景。