地铁应急接驳公交派车场站选择与行车计划协同优化

冯旭杰，宋晓敏，陈明星，何祥，李佳杰

（1.交通运输部科学研究院，北京 100029；2.福建省运输事业发展中心，福建 福州 350025）

0 引言

随着地铁网络化运营以及设施设备老化，突发事件的发生概率逐渐增大。应急公交服务是处理地铁突发故障的一种关键应对策略，可为故障区间提供应急接驳服务。开行地铁应急接驳公交，需要确定派车场站和接驳公交的行车计划。

目前，国内外学者对地铁故障情形下的应急公交服务已有关注和研究，取得了较多成果。Jin等[1]提出了应急接驳公交服务的三阶段优化方法，即生成公交路径备选集、公交路径选取、优化公交车辆分配和发车间隔。Kepaptsoglou等[2]提出了接驳公交服务的设计框架，包括设计候选路径以及公交分配。宋吉鹏[3]基于断面客流量研究了地铁区间故障时所需接驳公交数量的计算方法。Hu等[4]构建了考虑上下行的应急接驳公交非线性整数规划模型，并采用改进后的遗传算法求解；Gu等[5]以减少公交接驳时间和降低乘客延误为目标，建立了公交应急接驳优化模型，并采用启发式算法求解。部分学者以降低乘客延误、应急疏散时间等为目标，提出了应急接驳公交的实时调度优化方法[6-8]。在此基础上，Chen等[9]进一步考虑了应急接驳公交快慢车运营模式。

除应急接驳公交路径设计及调度优化，还有不少研究重点关注应急接驳公交派车场站的选址问题，已有较为丰富的研究成果[10-13]，特别是Revelle等[10]对设施选址问题进行了系统调查和阐述，Pender等[11]将设施选址理论和方法应用到公交接驳领域。聂鑫路等[14]针对城市轨道交通应急救援站选址问题，基于应急救援的时间及发生概率，提出以滚动式多步求解的方法建立粒子维度自适应模型。刘爽等[15]提出了应急接驳公交派车场站选择优化方法，其中地铁车站滞留风险权重由车站风险评价神经网络模型量化确定。邓亚娟等[16]进一步考虑了乘客等待时间延误，构建了应急接驳公交派车场站反向集合覆盖选择模型。何祖勇等[17]考虑了乘客等待时间容忍度，提出了应急接驳公交派车场站数量最少和时间惩罚成本最低的双目标模型，并利用ε-约束法将其转化为单目标优化模型。

然而，当前对派车场站选择的研究未充分考虑行车计划，而行车计划是影响应急接驳公交场站选择的重要因素：一方面通过开行快车可加快公交周转，从而减少所需公交车数量；另一方面通过行车计划可以更准确地计算乘客等待时间和时间损失。因此，本文在已有研究的基础上，构建地铁应急接驳公交派车场站方案选择与行车计划协同优化模型，在保证应急接驳公交周转可行的基础上，计算不同派车场站数量和行车计划下的乘客时间损失，确定最优的派车场站方案。

1 问题描述

本文以包含多条地铁线路的网络为研究对象，应急接驳公交需应对网络内所有地铁线路的潜在故障情形，因此应急接驳公交派车场站的选择需考虑根据历史运营数据分析得到的各线路故障发生概率。为权衡运营单位和乘客双方利益，本文考虑公交数量和乘客时间损失最小两个目标。

在地铁区间故障情形下，故障区间的车站将陆续聚集乘客，需通过应急接驳公交进行疏散。应急接驳公交沿着故障区间平行开行。本文考虑快车和慢车两种公交模式，快车仅停靠故障区间的两端车站以及区间内换乘站等重点车站，慢车则停靠故障区间内的所有车站，快慢车在上下行方向的开行路径完全相同并循环运行，直至故障结束。图1 为应急接驳公交派车场站与行车计划示例，图中线路3车站M9至M12故障，快车停站方案为M9-M10-M7-M12，慢车停站方案为M9-M10-M11-M7-M12。

为计算乘客时间损失以及确保公交周转的可行性，需得到各故障场景下应急接驳公交发车时刻表。本文对故障时段进行离散化处理，以1min为单位时间长度将时段等间隔划分为若干时间间隔。以最小化乘客时间损失为目标，可在各时间间隔分别决定故障两端车站是否发出一个公交快车/慢车，其中快车和慢车的发车决策需满足场站内车辆数量的约束，如图1所示的M9累计发出的车辆数应不大于派车场站B2和对向故障车站M12累计到达的车辆数。

2 模型构建

2.1 模型假设

本文模型主要基于以下假设：

（1）为尽快疏散地铁客流，应急接驳公交派车场站在地铁区间故障后将第一时间将公交车辆派往地铁故障区间的两端车站；

（2）为减少对正常运行公交的干扰，应急接驳公交的所有快车和慢车均从派车场站始发和终到，不从正常运行的公交中调度；

（3）公交快车和慢车在运行过程中不可改变车辆的快慢车属性，即在故障区间往返运行时，始终保持快车或慢车模式；

（4）对乘坐快车或慢车均可的乘客，其将优先选择快车以减少旅行时间；慢车的运输能力将优先保证仅能乘坐慢车的乘客。

2.2 模型建立

为权衡公交企业和乘客的利益，本文考虑应急接驳公交数量和乘客时间损失最小化两个目标，分别如式（1）和式（2）所示。其中，乘客时间损失包括乘客在故障地铁站的等待时间、可乘坐快车的乘客由于乘坐慢车所增加的旅行时间以及研究时段末仍滞留车站的乘客延误时间。

式（1）～式（2）中：f1为应急接驳公交数量；f2为乘客时间损失（min）；i为备选应急接驳公交派车场站编号，从1开始依次编号，其集合I表示为I={1,2,…,si}，si为备选应急接驳公交派车场站总数量；分别为备选公交派车场站i派出的应急接驳公交快车数量、慢车数量；k为地铁突发事件，从1开始依次编号，其集合K表示为K={1,2,…,sk}，sk表示地铁突发事件总数量；j为故障风险较高的地铁站，从1开始依次编号，其集合J表示为J={1,2,…,sj}，sj为故障风险较高的地铁站总数量；t为时间间隔（min），将研究时段按单位时长等分成时间间隔，从1 开始依次编号，其集合T表示为T={1,2,…,st}，st为研究时段按单位时长等分成的时间间隔总数量；分别为突发事件k下，t时刻在故障地铁站j等待可选择快车或慢车的乘客数和仅能选择慢车的乘客数；为突发事件k下，t时刻在故障地铁站j等待可选择快车或慢车但最后上慢车的乘客数；分别为突发事件k下，慢车、快车从地铁故障区间一端运行至另一端的时间（min）；αk为突发事件k的发生概率；δ为研究时段末仍滞留在车站的乘客延误时间的惩罚系数，本文取2。

模型主要约束如下：

（1）当备选公交派车场站i被选为最终派车场站时，才能服务故障地铁站j：

式（3）中：xi为0-1 变量，当选择备选公交派车场站i为最终派车场站时取1，否则为0；yij为0-1变量，备选公交派车场站i接驳故障地铁站j时取1，否则为0；其他符号意义同前。

（2）由于存放空间限制，公交派车场站存放公交数量需满足上限约束：

式（4）中：Ni为备选公交派车场站i停放的公交数量的上限值；M为极大的正数；其他符号意义同前。

（3）公交派车场站向故障地铁站进行应急接驳服务时，需满足最大服务半径的约束，即当公交派车场站超过此服务半径时，无法提供应急接驳服务：

式（5）中：dij为备选公交派车场站i和故障地铁站j之间的距离（km）；lmax为备选公交派车场站的最大应急接驳距离（km）；其他符号意义同前。

（4）在备选公交派车场站中选择p个作为最终的派车场站：

式（6）中各符号意义同前。

（5）应急接驳公交在地铁故障区间的两端车站发车必须满足公交数量的约束，并且根据假设，快、慢车不改变其属性，因此，需在两端车站对快、慢车分别进行考虑：

同时，需计算各时间间隔的上车乘客和等待乘客数。上车乘客可分为3 类：仅能上慢车的乘客，其数量计算公式见式（12）；上快车或慢车均可的乘客中最终上慢车的乘客，其数量计算公式见式（13）；上快车或慢车均可的乘客中最终上快车的乘客，其数量计算公式见式（14）。根据假设，上快车或慢车均可的乘客中最终上慢车的乘客数为慢车剩余能力（除去仅能上慢车的乘客）与等待乘客数（除去上快车的乘客）的较小值。等待乘客则分为2类：仅能选择慢车的乘客，其数量计算公式见式（15）；可选择快车或慢车的乘客，其数量计算公式见式（16）。

快慢车数量为正整数或0，其他决策变量为0-1变量：

式（17）～式（18）中：z为正整数；其他符号含义同前。

2.3 模型处理

式（4）、式（7）～式（10）、式（12）～式（14）为非线性约束，可通过引入0-1辅助变量进行线性化处理[18]，其余的线性约束利用线性求解器进行求解。同时，针对所建立的双目标优化模型，利用ε-约束法[17]进行单目标转化。即首先以式（2）为单目标求解最小乘客时间损失，随后可将式（2）进行一定松弛并作为模型约束，从而建立以式（1）为单目标的优化模型，如式（19）所示。

约束条件为式（3）～式（10）、式（12）～式（18）以及式（20）。

式（19）～式（20）中：各符号意义同前。

通过该处理，可利用ε的变化求得关于公交数量与乘客时间损失的帕累托（Pareto）最优解集。

3 案例分析

3.1 案例参数

以国内某城市的部分地铁网络（见图2）为例验证方法的有效性。该地铁网络包括7条线路，故障发生概率及客流需求等信息如表1 所示，故障发生概率较高的是表1中的7个区间：A2—A6、B4—B10、C6—C12、D5—D14、E8—E13、F1—F9、G4—G6。模型中公交派车场站数量p预设为7 个，公交最大接驳距离lmax取值为8km，公交载客能力C为80 人/车，选定19 个备选公交派车场站，场站停车能力及与故障地铁站的距离如表2所示，其中公交派车场站可接驳的故障地铁站已根据约束（6）和lmax进行筛选。案例采用Gurobi Solver 9.5求解。

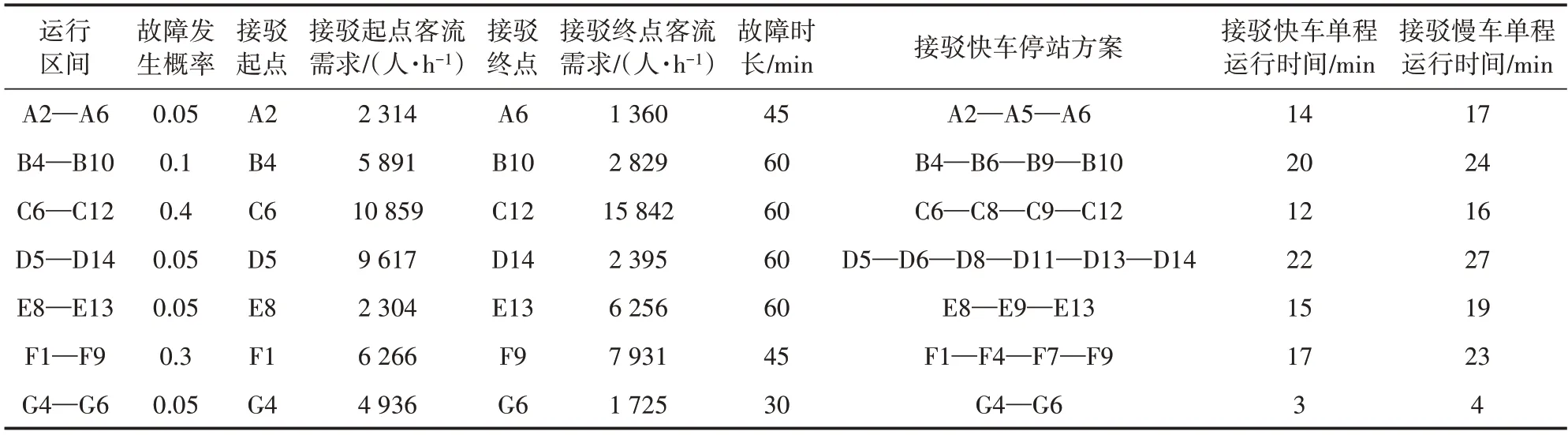
表1 地铁运行区间的故障发生概率、接驳客流需求和快慢车运行信息

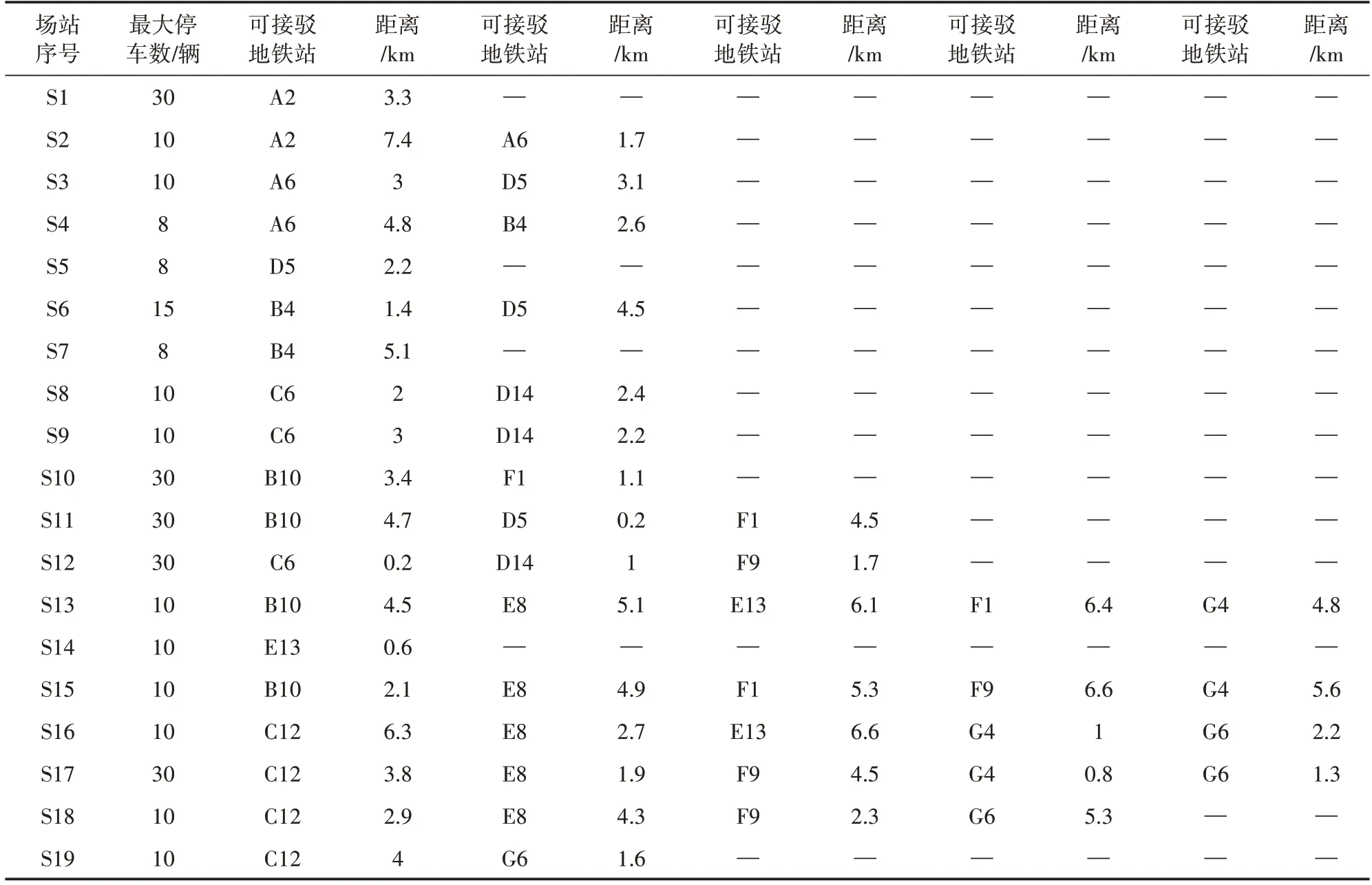
表2 备选公交派车场站停放能力以及与故障地铁站的距离

3.2 模型效果分析

为验证本文模型的有效性，将其与无快车模式的应急接驳公交派车场站选择方法（以下简称“无快车方法”）进行对比，即去除本文模型中的快车，公交车辆全部为慢车。同时，本文方法在每一时间点均可决策是否发出1 个快车/慢车，为确保对比的公平性，无快车方法在每一时间点可决策是否发出0/1/2个慢车。以乘客时间损失最小化为目标，利用Gurobi 求解本文方法及无快车方法，结果如表3和表4所示。

表3 本文及无快车方法的求解结果

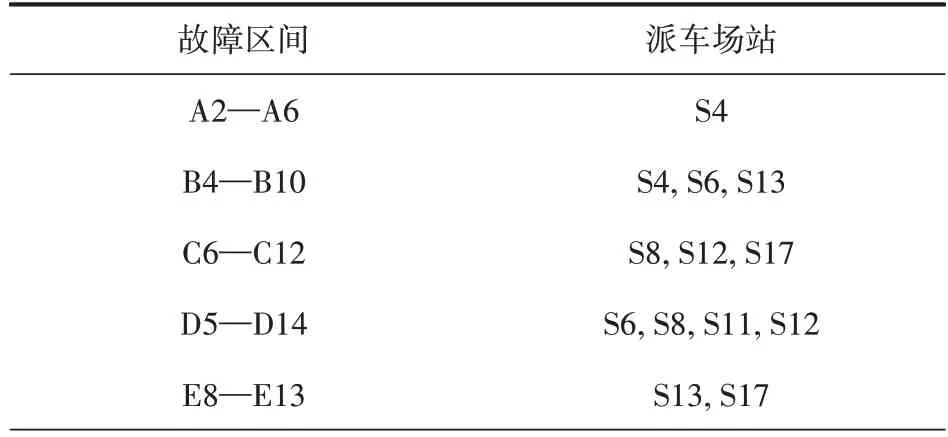
表4 故障区间的对应派车场站

表4 （续）

由表3 可看出，本文方法在不增加公交数量的情况下，通过快车模式加速公交周转，虽然增加了总发车次数，但使得乘客时间损失降低4.17%。以线路B 为例，线路B 的派车场站为S4,S6 和S13，图3～图5 为两种方法在线路B 的行车计划，本文方法和无快车方法的总发车次数分别为96（63 次快车+33 次慢车）和88，本文方法通过快车模式，虽然增加了总发车次数，但可在一趟全程运输（上行+下行）中节约8min。同时，由图3～图5可看出，公交车辆在上下行方向可有效衔接，保证了方案的可行性。

表3 为最小乘客时间损失目标下求解结果，通过调整ε取值，可求得本文方法的Pareto 最优前沿，如表5 所示。从表5 可看出，随着ε的增大，公交数量逐渐减少，从而减少了求解时间，但乘客的时间损失将增加。这是因为在松弛时间损失这一目标时，可以降低对应急接驳公交服务的需求程度，减少所需公交派车场站数量和公交数量。需要说明的是，案例设置了派车场站总数为7个的限制，最终所选派车场站数量可以少于7个，但不能超过7 个，根据派车场站数量的求解结果来判断该场站最终是否被选择。例如ε为1时，S4,S6 和S15 的快慢车数量均为0，此时的派车场站总数为4个，即：S12,S16,S17,S18。不同ε下，各方案通过派车场站以及快慢车数量的变化确定当前乘客时间损失约束下的最小公交总量。

表5 本文方法的Pareto最优前沿方案（ε灵敏度分析）

3.3 派车场站数量灵敏度分析

由于派车场站数量对本文方法具有重要影响，对派车场站数量进行灵敏度分析。

首先，在松弛派车场站总数为7个的限制下，以乘客时间损失最小为目标求解本文模型，结果如图6所示。

由图6 可看出，随着派车场站数量的增加，应急公交数量逐渐增多，而乘客时间损失则逐渐下降，但时间损失的下降速度逐步放缓，如派车场站数量从4增加到5和从9增加到10，乘客时间损失下降比例分别为9.6%和2.7%。主要原因在于各派车场站有最大停放能力的约束，在较少派车场站数量的限制下，能提供的应急接驳公交数量有限，导致乘客时间损失较大。随着派车场站数量的增加，乘客时间损失将得到降低，但所需的公交数量将增多，各公交平均承担的车次数量将降低，导致乘客时间损失下降速度放缓。

接下来，为进一步分析派车场站数量对本文方法的影响，固定公交数量（以派车场站7 个对应公交数量133辆为约束），求解乘客时间损失最小目标下的方案，结果如图7所示。

由图7 可以更明显地看出公交派车场站数量对乘客时间损失的影响：即使公交数量保持不变，派车场站数量的增加仍可有效地降低乘客时间损失。主要原因是多个场站分散布置可更好地兼顾整个地铁线网，从而更好地应对各线路故障情形。但派车场站数量进一步增加时，乘客时间损失的下降速度放缓，说明当前派车场站数量下应急接驳公交行车计划已接近最优，增加其他派车场站对乘客时间损失的降低空间不大。因此，应急接驳公交派车场站应尽可能地均匀分散选择，但也无需过量选择，可根据实际情况灵活确定。

4 结语

本文以地铁应急接驳公交场站选择与行车计划协同优化为研究对象，构建了所需公交数量和乘客时间损失最小化的双目标优化模型。利用ε-约束法将双目标模型转化为多个单目标模型，并利用Gurobi 求解模型的帕累托最优前沿。本文方法可为突发事件下地铁应急接驳公交派车场站选择和行车计划制定提供参考，决策者可根据实际需要，权衡应急接驳公交派车场站数量、公交数量以及乘客时间损失等指标，合理选择最终方案。然而，由于应急接驳公交停靠等运营方案具有多样性，构建接驳公交派车场站选择和公交运营方案的协同优化模型是下一步的研究方向。