内生转换回归模型理论与应用

王馨瑶 任钰田 李心仪

（东北农业大学 经济管理学院，黑龙江 哈尔滨 150030）

一、引言

在经典的多元回归模型中均有严格外生假定，但通常情况下该假定很难被满足，所以学者们只要求同期外生，即弱外生性假定，要求扰动项与解释变量同期不相关。然而，现实中这一假设也可能无法实现，从而出现内生性问题。因为内生性问题会破坏参数估计的一致性，使估计结果不具备参考价值，所以对内生性问题加以解决也是实证研究中的重要问题。一般而言，出现内生性问题的原因有四种：第一，遗漏解释变量；第二，解释变量与被解释变量互为因果，有时也称反向因果关系；第三，自选择问题；第四，测量误差问题。现有多种方法可解决内生性问题，比如双重差分法、工具变量法等。但在实证研究中，个体观测很可能是一个选择后的结果，由于只能观测到个体的选择行为以及选择后的结果，直接将结果变量对决策变量回归可能存在遗漏变量的内生性问题，所以可利用内生转换回归模型 （Endogeneous Switching Regression Model，简称ESR）来缓解这类问题。

Maddala和Nelson（1974）最早在转换回归模型的基础上提出内生转换回归模型，用以解决样本选择偏差所带来的内生性问题［1］。早期运用该模型的经典研究包括：Lee（1978）的工会薪酬模型，该模型涉及有工会部门和无工会部门这两种选择，通过选择模型确定个人是否加入工会，并分别利用模型考虑两种选择时的工资情况［2］；Thorst（1977）的住房需求模型，该模型涉及拥有住房和租用住房两种选择，利用选择模型加以确定并分析两种情景下的支出情况［3］；Adamchik和 Bedi（1983）的公私营工资模型，该模型使用波兰数据从预期收益和在特定部门工作的相关好处等方面经验分析公营和私营条件下工人的工资差异［4］。

内生转换回归模型是一种拓展的Heckman选择偏差矫正模型，较Heckman选择模型而言具有明显优势。Heckman模型只能根据可观察到的关系方程研究解释变量和被解释变量之间的关系，比如研究是否有孩子与工资之间的关系，但对于没有工作的部分人而言不存在工资这一被解释变量，从而因缺失值的出现造成样本选择偏差。此时，一般通过观察样本中的逆米尔斯比率纠正样本分布，再估计两者之间关系。而内生转换回归模型可通过同时关注到的两种选择情景下的实际情况推演被解释变量和解释变量之间的关系，并放松必须将共同影响因素全部纳入方程的假设，除此之外，选择方程也会受到两种情境下被解释变量的影响，如选择方程为是否加入工会，这一选择将会同时受到公共部门的工资和私有部门工资的影响，故利用内生转换回归模型可有效改善估计结果无效、有偏的问题。且内生转换回归模型考虑了处理效应的异质性问题，其在项目、政策效果评价方面均优于最小二乘估计 （OLS）和倾向得分匹配（PSM）方法［5］。传统的回归模型只能估计影响效应，不能同时观测同一个体在选择不同情景下时的行为，因此不能对比影响效应，而内生转换回归模型可以通过拟合实现反事实推断，从而更好比较项目、政策的影响效果。正因为内生转换回归模型具有这些优势，近些年国内学者也开始广泛运用此方法以解决样本选择带来的内生性问题，尤以2019年至2021年为主，研究多集中于农业经济学领域。

二、理论研究

两阶段方法利用两个回归方程描述所表达的行为，并用一个准则函数Ii决定两个方程式中的一个适用方程，方程式表达为：

这个模型与Goldfeld和Quandt（1973）所提出的转换回归模型相类似，但是假设μi与μ1i和μ2i相关，故该转换模型被 Maddala和 Nelson（1974）［1］称之为内生转换回归模型（ESR），该模型分为两个阶段：

第一个阶段为选择方程，这个选择会带来结果上的差异Ii*，这一差异不能被直接观察到，可利用方程表达为：

第二个阶段为结果方程，针对选择情况分别分析影响因素，设定形式为：

方程 （4） 和方程 （5） 中 Zi是影响 y1i和 y2i的外生向量集，Xi可以与Zi重合，但需要存在至少一个属于Xi却不属于Zi的变量，这类变量相当于工具变量。假设选择方程 （3）、结果方程 （4） 和结果方程 （5） 的随机误差项μi、ε1i和ε2i均服从均值为0、方差为σ的三元联合正态分布，其协方差矩阵形式可表示为：

其中，F和f分别为累积正态分布函数和正态密度分布函数。

内生转换回归模型中，相关系数ρ1i（ρ1i＝σ1i2/（σiσ1i） ） 和ρ2i（ρ2i＝σ2i2/（σiσ2i） ） 分别表示方程 （3） 与方程 （4） 和方程 （5） 误差项之间的协方差，ρ1i和ρ2i的计量意义包括：第一，当ρ1i和ρ2i在统计水平上显著时，说明存在不可观测因素，其导致了选择偏差，为得到具有一致性的估计结果，须同时考虑可观测和不可观测因素，选取内生转换回归模型是适宜的；第二，当ρ1i和ρ2i具有不同的正负性时，说明已根据自身比较优势做出了理性决策，当ρ1i和ρ2i是同正或同负时，说明不需要考虑选择情况；第三，当ρ1i＞0时，说明存在负向的选择偏差，当ρ2i＜0时，说明存在正向的选择偏差［6］。当存在较大相关系数时，使用最大似然法估计过程会难以收敛，通过蒙特卡罗模拟表明，校正残差可以解决几乎所有情况下的问题［9］。

当存在不可观测因素使得corr（μi，εi）≠0时，需在第一阶段估计选择方程，并通过其计算逆米尔斯比率λ1i、λ2i以及协方差项σ1i＝ cov （μi，ε1i） 和σ2i＝ cov （μi，ε2i），将其带入两个方程中以校正由于不可观测因素导致的选择偏差，其扩展形式为：

利用方程 （6）和方程 （7）估计出相关系数后，可计算出三种平均处理效应，分别是处理组的平均处理效应 （ATT）、对照组的平均处理效应 （ATU）以及总体样本的平均处理效应（ATE）。但因都包含了没有受到相关政策影响样本的处理效应，所以对照组和总体样本的平均处理效应在评估政策方面的意义不大，最重要的估计参数为处理组的平均处理效应。虽然在自选择问题上，可以通过倾向得分匹配法进行控制以获取平均处理效，但倾向得分匹配法存在一个主要缺陷，即只能控制由于可观测因素带来的选择性偏误，却不能控制由于不可观测因素所带来的选择性偏误。

利用内生转换回归模型估计平均处理效应时，可将可直接观测的事实水平用方程表示为：

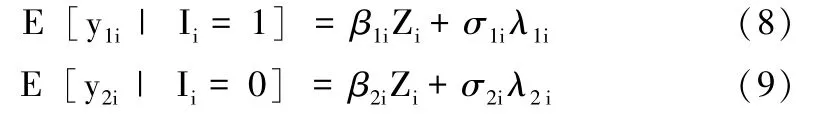
可将不可直接观测的反事实水平用方程表示为：

由此可将平均处理效应表达为：

可使用两阶段最小二乘法 （2SLS）或最大似然法 （MLE）估计内生转换回归模型中的选择方程，但是这两种方法估计出的参数有效性较低，并需要繁琐调整才能得到一致的标准误差。因此，Lokshin和Sajaia于2004年将Terza（1998）的计数数据回归模型进行扩展提出了完全信息极大似然估计 （Full Information Maximum Likelihood，FIMI），这种方法可以同时估计选择方程和结果方程，直接得到一致的标准误差，但该方法计算量较大，需通过Stata软件实现［7］。并且使用该估计方法有一定前提，即选择方程需为二值选择方程，结果方程的误差项需要符合联合三元正态分布。如果ε1i和ε2i与μi不能满足服从联合正态分布的假设，那么所得估计结果将会产生偏差，故在某些应用中存在适用性问题［8］。此时，可利用 Terza（2008）提出的两阶段残差嵌入方法 （2SRI），这一方法放松了正态分布假定［9］。除此之外，也可使用Probit估计方法对选择方程进行估计，这类模型被特定称为内生转化概率模型 （Endogeneous Switching Probit Model，ESP）。

三、应用研究

（一）内生转换模型的应用领域

由于内生转换模型在应对选择性偏差等可观测及不可观测的内生性问题上具有天然优势，近年来运用内生转换模型的实证研究成果层出，主要应用领域包括经济学、管理学、社会学及其交叉学科，其中农业经济学和社会经济学方面的应用研究更为广泛。

在农业经济学方面，利用内生转换模型进行的学术研究集中于四个主题：第一，研究对农户收入的影响，影响因素包括信贷配给、选择使用先进生产技术与模式［10－12］。第二，研究对农业产出的影响，包括采用适应性生产技术措施等变量［13－14］。第三，研究种植改良农产品或有机认证农产品的影响［15－17］； 第四，研究应用互联网等现代科技的影响［18］。除此之外，内生转换模型同样能为涉农政策评价提供基础。利用内生转换回归模型构架 “反事实”分析框架，估计集体林地确权到户、捕捞法规等涉农政策的作用效果［19－20］。

在社会经济学方面，从个人层面分析公共部门和私营部门之间的工资差距是最主要的也是早期研究的重点领域，目前已被应用研究荷兰、秘鲁等国家的具体情况［21－22］，也有学者研究工会的参与情况以及是否为全日制工作对工资的影响［23］。从企业管理层面研究对企业投资的影响［24］，从政策评价层面分析土地政策等的政策效果［25］。

（二）农户投保行为对家庭收入的影响效应分析

1、理论基础

农户是否投保的行为往往受农户人力资本、金融资本、社会资本、物质资本和自然资本等要素的影响［26］。参考已有研究，本文将性别、年龄、农作物种植年限、风险态度等户主个人特征，家庭兼业化程度、家庭债务贷款情况等家庭生产特征以及以是否遭受过自然灾害来表示的自然特征纳入农户投保行为方程中。现有研究表明政策性农业保险对农户收入存在正负两种效应：负效应表现为当没有灾害发生时，农户购买保险导致的家庭收入减少。在投保农业保险后农户疏于防范、不制止受灾范围继续扩大等道德风险问题造成的家庭收入大幅减少。以及农户投保行为导致的生产要素配置改变最终提高农作物产出，但在市场机制下农产品价格降低带来的收入减少；正效应表现为农业保险对农业生产风险的转移和补偿，促进农户灾后恢复再生产，稳定并提高农户家庭收入。或通过促进农业产业结构调整、农村金融发展以及农业技术创新，提高农业生产效率和农产品质量，以此增加家庭收入。

虽然现有研究已探讨政策性农业保险与农户家庭收入的关系，但针对政策性农业保险究竟是提高还是降低农户家庭收入这一核心议题仍没有定论，造成研究差异的主要原因有两点：第一，农业保险对农民收入的影响机制是具有复杂性和多样性的；第二，与不同研究所使用的不同样本、数据以及方法有关，尤其是实证方法选用上，当未充分考虑农户生产行为与投保行为可能存在一定的 “同时决策”，且存在投保决策的自选择问题时，就会出现严重的内生性情况，在数据方面现有研究以宏观数据为主。因此，本文基于微观调研数据利用内生转换模型对这一问题加以解决，研究政策性农业保险的农户投保行为对农户家庭年收入的影响，以期得到更为合理的研究结果。

2、数据来源与变量说明

本文所使用的数据来源于相关课题的调研，以黑龙江省政策性农业保险开展较好的具体代表性的地区，即绥化市、齐齐哈尔市、佳木斯市以及鹤岗市为调研对象展开实地调研，共对上述4个市的9个县发放问卷405份，回收有效问卷364份，问卷有效回收率为89.88%。据统计，2019年黑龙江省成灾面积占主要农作物播种面积之比为11.89%，农业保险在分散农业自然风险、平滑农民家庭收入方面都发挥着重要作用。按照经营主体划分，364个调研对象中有28个农业合作社、82个种植大户以及254个普通农户，其中将种植面积在200亩以上的农户定义为种植大户。如表1所示，364个样本中有232户选择投保农业保险，占样本总数的63.74%。从户主特征来看，投保组与非投保组差别不大，相较于非投保组，投保组农户更加年轻，受教育程度更高，农业种植经验更少，对政策性农业保险的评价更为满意。从家庭特征来看，投保组的家庭总人口数更高，间接说明从事农业生产的劳动力更多，并且农户家庭年农业收入和现有的债务金额均较高。从生产特征来看，投保组经营种植的土地面积明显高于非投保组，且整体经营土地面积均较高，符合黑龙江省的自然地理特征。从自然特征来看，投保组农户之前遭受过自然灾害的比例高于非投保组农户。

表1：变量设置及说明

家庭特征家庭总人数 农户家庭人口总数 （人） 2.27 1.91家庭收入 农户家庭年农业收入 （万元） 136.71 30.50债务水平 农户家庭现有债务情况 （万元） 35.31 8.52生产特征经营主体 农户的生产经营主体的确定。农业合作社＝1，种植大户＝2，普通农户＝3 2.62 2.62农业生产兼业化程度 农户家庭生产经营类型。纯农业经营＝1，农业为主兼营其它＝2，非农业为主兼营其它＝3，非农业经营＝4 1.45 1.44耕地面积 农户经营土地面积 （亩） 961.56 268.79土地流转情况 农户经营土地是否存在流转行为 0.85 0.89自然特征 受到灾害影响 农户是否受到过自然灾害影响。无＝0，有＝1 0.79 0.63

3、模型构建

结合本文的研究目的与理论基础，构建的农户投保行为方程为：

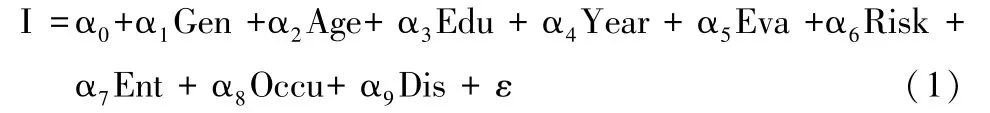
（1）式中，I为农户是否购买政策性农业保险；Gen为户主性别；Age为户主年龄；Edu为户主受教育程度；Year为农业种植经验，用户主从事农业生产年限表示；Eva为户主对于政策性农业保险的服务评价；Risk为户主风险态度，用户主是否购买商业型农业保险表示；Occu为农户生产兼业化程度，用农户家庭生产经营类型表示；Dis为农户是否受到过自然灾害影响；ε为随机干扰项。

构建的农户投保政策性农业保险对农户家庭收入的影响效应方程为：

（2）式中，Inc为农户家庭收入；Num为农户家庭总人数；Fin为农户家庭债务水平；Acre为农户耕地面积；Land为农户经营土地是否存在流转行为；μ为随机干扰项，其它变量含义同前式。

内生转换模型将 （2）式转化为 （3）式和 （4）式，以分别表示投保组和非投保组农户的投保行为对其家庭收入的影响，具体方程为：

（3）式中的IncT和 （4）式中的IncU分别表示投保组和非投保组的农户家庭收入。当不可观测因素同时影响农户投保行为和农户家庭收入时，投保行为方程和农户家庭收入方程的残差项就会存在相关关系，造成OLS估计的结果有偏。由于实际情况的限制，农户投保和不投保的行为不能同时发生，也就是说IncT和IncU不能被同时获得，ESR将该问题视为数据缺失，所以将农户投保行为方程 （1）式中计算得到的逆米尔斯比率λ引入收入效应方程，对这一问题加以来解决。此时，投保组和非投保组的投保行为对农户家庭收入的影响效应方程将分别转化为：

（5）式和 （6）式中，λT和λU表示观测不到的农户能力或偏好致使的投保选择，σTε＝cov （μT，ε） 和 σUε＝ cov （μU，ε）表示行为方程和收入效应方程误差项的协方差，若二者在统计意义上显著，则表明十分有必要利用内生转换模型解决自选择问题。待已纠正不可观测因素导致的偏差问题后，（5）式和（6）式得到的估计结果将是无偏的和一致的。本文选择完全信息极大似然估计法 （FIMI）对行为方程 （1）式和收入效应方程 （5）式、（6）式进行估计，对农户投保行为的收入效应进行反事实分析，比较投保农户与非投保农户在现实与反事实条件下农户家庭收入间的差异，以准确评价农户投保所引致的收入变化。

投保组和非投保组的家庭收入的条件期望可表达为：

而投保组和非投保组的反事实家庭收入的条件期望可表达为：

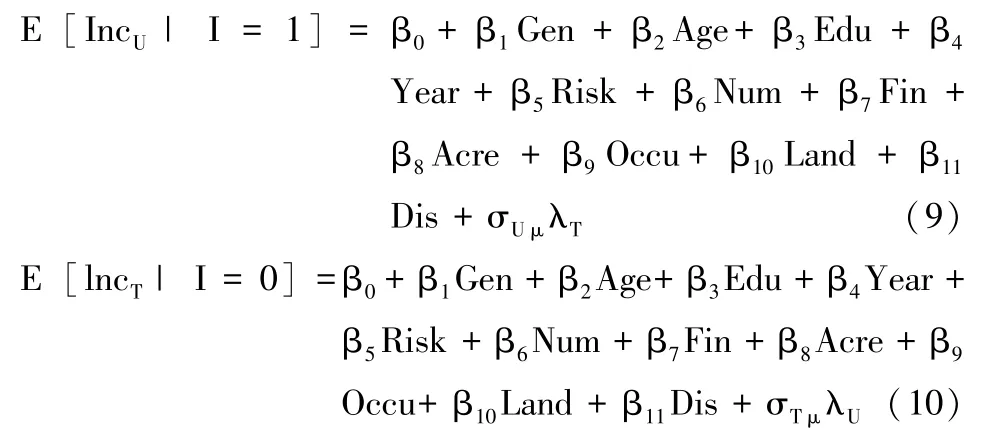
实际投保组农户家庭收入的平均处理效应，即处理组的平均处理效应ATT可表示为 （7）式与 （9）式之差，具体表达式为：

（11） 式中，XT为 （3）式中的解释变量，βT和βU分别为（7）式和 （9）式中的参数估计结果。

实际未投保组农户家庭收入的平均处理效应，即非处理组的平均处理效应ATU可表示为 （8）式与 （10）式之差，具体表达式为：

（12）式中，XU为 （4）式中的解释变量，βT和βU分别为（8）式和 （10）式中的参数估计结果。

4、实证结果

由表2所示的农户投保行为的收入效应方程的实证估计结果可知，经营主体的类型，农户的风险态度以及生产兼业化程度是决定其投保行为的重要因素，即农户的生产专业化程度越高，其投保概率越低，风险意识较强的农户更会选择购买政策性农业保险，尤其以大规模农户为主。由于表中ρUε与联合独立似然比均通过了1%水平的显著性检验，故证明了内生转换模型的适用性。根据表中投保组与非投保组投保对家庭收入的影响效应方程的实证估计结果可知，对于投保组来说，户主受教育程度、生产兼业化程度以及负债水平越高，家庭总人数越多，经营土地面积面积越大，则越能促进投保组农户家庭收入的提高，而即使已投保政策性农业保险，自然灾害的影响仍会对农户家庭收入产生不利影响；对于非投保组来说，较投保组而言其风险态度对家庭收入有重要影响，在未购买政策性农业保险的情况下，越具有风险意识的家庭其收入的增加效果越明显。

表2：农户投保行为及家庭收入的内生转换模型实证估计结果

由表3所示的农户投保行为对农户家庭收入的处理效应可知，投保农户家庭收入的平均处理效应 （ATT）为1.235，未投保农户家庭收入的平均处理效应 （ATU）为1.313，表明购买政策性农业保险有利于提高农户家庭收入。

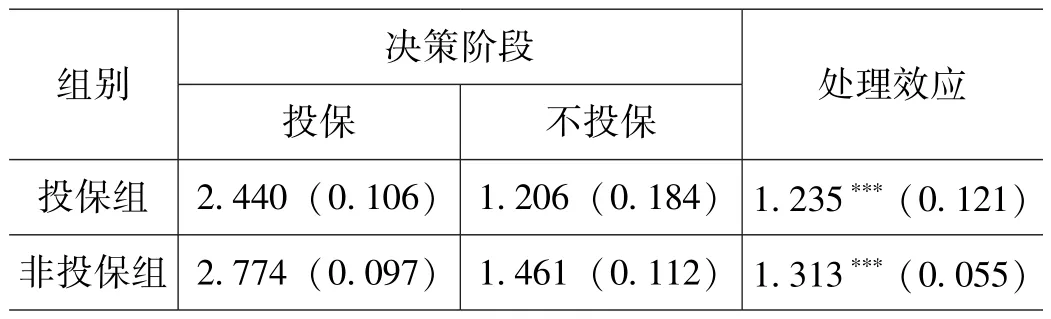
表3：农户投保行为对家庭收入处理效应的测算结果

根据经营主体划分，农业合作社、种植大户以及普通农户的政策性农业保险的投保率分别为75%、76.83%和72.44%，相较而言，普通农户的投保率较低，故为检验投保对于普通农户的收入影响效应的具体情况，本文测算普通农户的投保行为对其家庭收入的处理效应。如表4所示，投保的普通农户家庭收入的平均处理效应 （ATT）为0.665，未投保的普通农户家庭收入的平均处理效应 （ATU）为0.569，虽然其增收效应不如总体效果好，但也可证明对于政策性农业保险的主要需求者来说，普通农户购买政策性农业保险有利于提高其家庭收入，对于普通农户的增收效应明显。

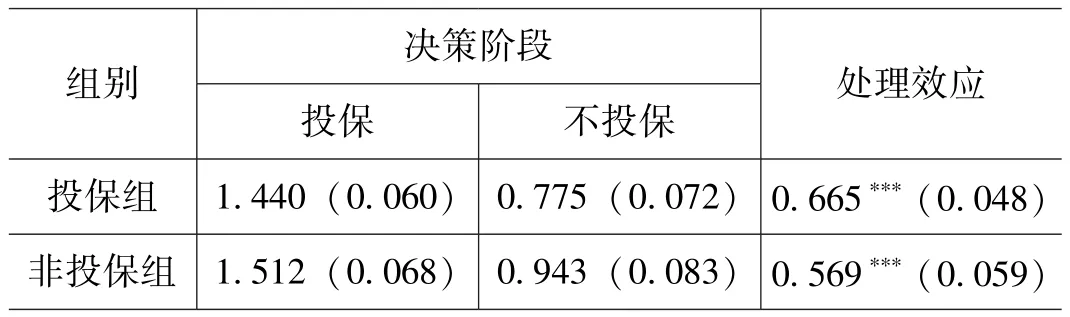
表4：普通农户的投保行为对家庭收入的处理效应测算结果

四、总结

内生转换回归模型作为转换回归模型的一种，在不断发展中日益得到完善，是经典实验设计的自然扩展。并且因其在解决内生性问题以及评价项目、政策效果方面的独特优势，在计量经济学文献中被较为普遍地使用。其中国外学者使用此方法进行的研究较为丰富，主要集中在农业经济学领域上，国内从2018年开始逐渐流行此类研究，且不仅广泛应用于农业经济学领域也涉及社会经济学领域，研究层次均较高。现有研究多关注于涉及二值选择的有限因变量内生转换回归模型，虽连续变量的内生转换回归模型也有应用，但研究数量较少，所以在未来的研究中可以将此类模型通用化，并进一步发展有限因变量的研究。本文利用内生转换回归模型实证分析农户投保政策性农业保险的收入效应问题，充分利用该模型解决因农户投保行为的自选择性质所带来的内生性问题，并评价政策性农业保险的政策效果。使用黑龙江省农户作为研究对象，得到投保政策性农业保险可以促进农户增收的结论，与现有研究结果相一致［27］，并且充分考虑了内生性问题，结果具备合理性。据此，应推动保险公平，注意对普通农户进行保险宣传，提高其风险防范意识，并提高农户整体投保水平。