基于SOLO理论的高中数学教学设计——以分类加法计数原理与分步乘法计数原理为例

王 宇

(哈尔滨师范大学教师教育学院，黑龙江哈尔滨，150000)

SOLO(Structure of the Observed Learning Outcome)是对皮亚杰的儿童认知发展阶段理论的继承和发展，本质上是一种认知发展理论.经过大量的研究发现，学生不仅是成长的总体阶段会呈现阶段性趋势，当他们学习或者解决某个问题时也同样会表现出阶段性的外显特征.SOLO能够对学生每个反应进行分类，并且SOLO理论中的思维方式具有累积性，即一种思维方式的出现并不替代以前的思维方式，后发展起来的思维方式与早先形成的思维方式可以并存.约翰·比格斯认为，学习结构的复杂性主要包括两个方面：一是量的方面，即学习要点的数量；二是质的方面，即如何建构学习要点.根据这两方面要求，约翰·比格斯把学习结果分为SOLO的5个水平.

五种反应水平具体判断标准如下：

表1

关注学生在问题教学中的表现就能知道他们的思维水平在什么结构层次，这样我们的教学设计就更具有针对性.

1 利用SOLO分类理论准确把握数学教学目标

课前学生的思维结构处于前结构水平，教师可以通过一些感性材料或者对旧知的复习、实验的操作引导学生向单点结构水平过渡来学习概念、公式、定理等基础知识；然后通过对知识进行辨析、解读，从多角度发现和理解知识的内涵，达到多点结构水平；最后，使学生的思维水平向关联结构层次发展，将以上学习的各方面知识综合到一起，实现知识的应用.并积极引导学生进行知识的迁移和运用进而努力达到扩展抽象水平.

以人教A版高中数学选择性必修第三册第六章第1节“分类加法计数原理与分步乘法计数原理”教学为例，《普通高中数学课程标准(2017年版)》中关于两个基本计数原理的学习在知识层面上要求学生“理解分类加法计数原理和分步乘法计数原理及其作用”；在思维层面上要求学生“结合具体情境，理解许多计数问题可以归结为分类和分步两类问题”“能根据计数原理分析问题”“能运用这些原理解决简单的实际问题”，在内化学习内容的同时掌握一定的解题方法和解题技巧.根据以上述分析，得出分类加法计数原理与分步乘法计数原理教学目标如下：

(1) 从实例出发，并能正确“完成一件事”；(单点结构)

(2) 通过对问题进行比较能够总结得出两个计数原理；(单点结构)

(3) 通过对问题特征的分析，能描述“完成一件事”的具体含义，明确分类与分步的区别，总结出应用两个计数原理的基本步骤；(单点结构/多点结构)

(4) 能正确选择和利用两个基本计数原理解决一些简单问题；(关联结构)

(5) 体会两个计数原理所包含的划归与转化、分类与整合和特殊与一般的思想方法；(关联结构)

(6)理解如何求子集的个数.(拓展抽象)

2 利用SOLO理论明确教学重难点

数学课堂教学中要着力于重点的分解以及难点的破解.分解教学重点就是帮助学生比较容易地接受新知识，同时努力减轻学生的压力；教学难点的破解就是在分析学生所学新知识与学生已有的认知水平之间存在的落差的基础上，搭建适当的脚手架.在利用SOLO分类理论对教学目标进行分析后，可以结合学生的实际情况确定教学的重点和难点.以人教A版高中数学选择性必修第三册第六章第1节“分类加法计数原理与分步乘法计数原理”为例，教学重难点设计如表所示.

3 利用SOLO分类理论设计教学内容

设计教学的最佳途径是依据所期望的教学目标来安排工作.这里的期望包括《普通高中数学课程标准(2017年版)》中的教学要求，也包括学生学情.以SOLO分类理论为指导进行课堂教学，就要以最终期望学生达到的思维结构层次为出发点，思考要想学生的思维结构发展到关联结构水平，并且最终能够达到扩展抽象水平.通过这个思考过程，就能很容易明确可以引导学生的思维水平向各个阶段发展的具体的教学任务.

片段一：情境引入，提出问题(第1课时)

请同学们观察实际生活中“衣、食、住、行”各方面存在的数学问题：

“衣”：高考后的假期，小王和同学约好前往景区游玩，出门前，她从两顶不同的白色帽子或三顶不同的红色帽子中选择一顶佩戴，共有多少种戴法？

“食”：景区午饭有比萨或意面各三个口味可供选择，如表3-1所示：

表3-1

小王从中任选一个口味的一种午饭食用，共有多少种选择？

“住”：由于天气原因，小王决定在景区暂住一晚，民宿还剩4个下铺或2个上铺，选择一个床位住宿，共有多少种选择？

“行”：第二天可以乘共享单车或观光车从景区返程，景区有40辆共享单车和8辆观光车，要顺利返程共有多少种选择？

问题1：对于我们生活中“衣、食、住、行”各方面遇到的数学问题，大家能否用已掌握的数学知识来进行解决呢？(引导学生从生活情境中提炼数学问题，并利用枚举法对问题进行思考及解决)

设计思路：课前学生的思维水平处在前结构水平，此时教师需要提供给学生进入新课程的指向.设置生活中学生经常会遇到的大量繁杂的计数问题能够激起学生的兴趣，此时学生产生想要探究这些计数问题背后蕴藏的特定原理的兴趣和冲动，达到通过情景和问题引导学生快速过渡到单点结构水平的效果.

片段二：问题探究，归纳原理(第1课时)

问题1：请尝试从“什么事情”“如何解决”“结果怎样”三个方面对上述问题进行再次观察并将表格填写完整.

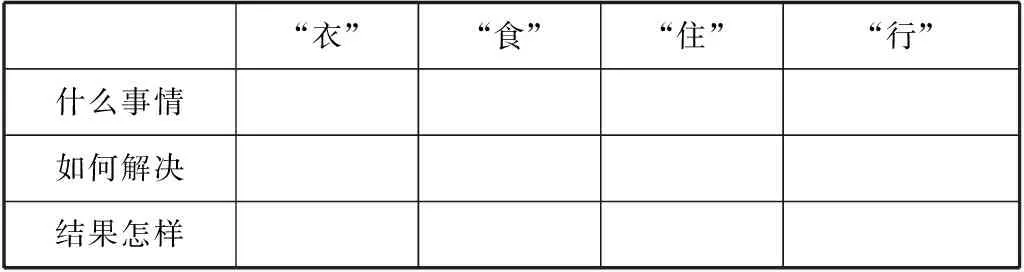
表3-2

问题2：能否根据这四个问题的解决办法尝试抽象概括出一般结论？

表3-3

设计思路：此时学生的思维水平处在由单点结构层次向多点结构层次过渡时期，设置表格填空问题是为了帮助学生探究疑难、发现规律、形成结论，从而解决重点.表格将四个问题有机地整合在一起，更是为学生能够抽象出结论打下基础.

片段三：演练反馈，方法总结(第2课时)

通过上节课的学习我们已经知道了要运用两个计数原理解决问题的关键是要弄清完成“什么事情”、应该“如何解决”、最终“结果怎样”.那对于一个计数问题应该怎么完成？怎样进行分步或分类呢？

问题1：书架的第1层放有4本不同的计算机书，第2层放有3本不同的文艺书，第3层放有2本不同的体育书.

(1) 从书架中任取1本书，有多少种不同的取法？

(2) 从书架的第1， 2， 3层各取一本书，有多少种不同取法？

追问1：从书架中取2本不同种类的书，有多少种不同的取法？

问题2：能否总结出应用分类加法计数原理及分步乘法计数原理“完成一件事”的基本步骤？

设计思路：此时学生处于多点结构水平，继续从解决问题出发时学生不再毫无头绪，且问题及追问循序渐进，能够把学生的所思所想串联到一起.通过对题目中关键词的辨别，引导学生从中发现并总结出解决问题的关键及步骤，突出强调弄清完成一件事的要求至关重要，进一步弄清“完成一件事”的具体含义，并且能够准确区分分步和分类，从而达到多点结构水平.

片段四：原理再用，巩固提高(第3课时)

问题：在国庆长假期间，班主任要从7名值周生中选若干人在7天假期值班且每天只需1人值班.

(1) 有多少种可能的安排方法？

(2) 若要求不能出现同一人连续值班2天，有多少种可能的安排方法？

(3) 你能够设计出贴近我们学习和生活并且能够运用分类加法计数原理和分步乘法计数原理解决的问题吗？

设计思路：通过SOLO分类理论可以将习题的作用发挥得更加积极.此题目属于关联思维结构水平习题，学生首先必须十分明确分类与分步的区别，同时掌握运用基本计数原理解决问题的关键.另外让学生编制题目，经历从解决问题到提出问题的过程，发展“命题人思维”更能让学生融会贯通应用计数原理，虽然可能稍有困难，但过程中充满探索的趣味.

片段五：总结提高，认知升华(第3课时)

问题：通过本节课的学习，你认为你在解决问题方面有何收获？

设计思路：把课堂时间归还给学生，让学生自己进行总结.通过梳理表格或思维导图等多样性的方式，引导学生进一步完善知识体系并加深理解和认识.

4 利用SOLO分类理论讨论教学评价

鉴于人的思维层次从关联水平提升到拓展抽象水平需要付出巨大的努力，因此要求所有的学生会达到或者希望达到更高层次是很不现实的.因此对于中学学生数学学习效果的评价要基于实际去进行，若期望偏离实际反而会导致呈现出一个不成功的课堂.因此，在正式教学之后，教师需要依据适量的标准来对学生的学习效果进行评价.

如果一个学生遇到新的或者他所不熟悉的题目类型，将会做出较低水平的回答.也就是说，如果要测试一个人的最佳表现，就需要让他获得大量的测验练习和经验，然后才能进行测评.因此，在利用SOLO分类理论进行评价时，只有当一个学生对题目类型经过练习巩固有一些经验后，他的最佳表现才能被评价，这是符合我们的教学经验的.可以以“SOLO分类评价理论”为基础，由学生回答问题的水平，统计学生的学习成果.在完成统计之后，教师可以通过统计的结果进行自我教学评价，如果教学某一知识点时，显现低级水平的学生较多，那么教师就需要思考教学过程是否出现了问题.

例如，如图1，以一道基本计数原理题为例：从甲地到乙地有2条路，从乙地到丁地有3条路；从甲地到丙地有4条路，从丙地到丁地有2条路.从甲地到丁地共有多少条不同的路线？

图1

若学生在分析题目后只能联想到运用分类加法计数原理或分步乘法计数原理，但是无法深入思考，无法解决问题，则反映出学生呈前单点结构水平.

若学生能够从题目中考虑到从甲地到丁地需要分步完成且共有两条路线，即甲地→乙地→丁地或甲地→丙地→丁地，但是不能够表述出两条路线间的内在关系，则此时反映出学生呈多单点结构水平.

若学生能够考虑到乙地、丙地间的区别与联系，能够考虑到多方面多角度进行解题，则此时反映出学生呈关联水平.

SOLO分类理论是教学评价中的一个重要工具及要素.在完成评价后，教师需要根据学生呈现出的结果对自己的教学进行总结与反思并对教学方法、教学内容等形成经验或判断.具体应该怎样实施还需要教育工作者根据实际进行变通和调整.