线性回归分析在某电商店铺指数预测中的应用
李小宇
(对外经济贸易大学 统计学院,北京 100085)
1 绪论
1.1 研究问题的背景、目的以及意义
投入产出比(ROI)对店铺广告投放来说非常重要,其可以反馈一个单品在市场的未来表现情况。文章运用线性回归分析的方法对某店铺的“推广产出”建立预测模型,然后运用建立的模型对未来一段时间的某店铺的ROI指数进行预测,从而对一家电商公司未来一年的经营情况进行预判。
1.2 研究的主要内容
文章基于某店铺2020年6—12月的投入产出数据,结合所学知识,先介绍了研究该问题的背景、目的及意义,然后介绍了建立该模型时需要用到的概念以及方法,对该序列建立合适的模型,在检验该模型的有效性之后运用该模型对未来一段时间的某店铺投入产出比(ROI)进行短期预测,检验该模型是否合理有效。
1.3 投入产出比(ROI)的概念
投入产出比(ROI)是一个判断店铺广告投放的重要指标。通过对行业数据的对比,结合店铺毛利、在店铺广告费用一定的情况下,投入产出比(ROI)大于12时,店铺广告投放处于良性状态,投放的越多,店铺收益越多。当店铺投入产出比低于12时,店铺广告投放处于非良性状态,如果扩大投放力度,店铺将处于亏损状态。
2 应用回归分析理论知识概述
2.1 一元线性回归的定义
一元线性回归分析,是根据自变量和因变量的相关关系,建立与的线性回归方程进行预测的方法。由于市场现象一般是受多种因素的影响,而并不是仅仅受一个因素的影响,所以应用一元线性回归分析预测法,必须对影响市场现象的多种因素做全面分析。只有当诸多的影响因素中,确实存在一个对因变量影响作用明显高于其他因素的变量,才能将其作为自变量,应用一元线性回归分析市场预测法进行预测。
一元线性回归分析法的预测模型为:
=+
式中,代表期自变量的值;代表期因变量的值;、代表一元线性回归方程的参数。
、参数由下列公式求得(用代表):
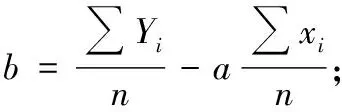

与表示的含义:每平均增加一个单位,平均增加个单位。
2.2 多元线性回归的定义
两个或两个以上自变量的回归称为多元线性回归。由于各个自变量的单位可能不一样,比如说一个消费水平的关系式中,工资水平、受教育程度、职业、地区、家庭负担等因素都会影响到消费水平,因此自变量前系数的大小并不能说明该因素的重要程度。将所有变量包括因变量都先转化为标准分,再进行线性回归,此时得到的回归系数就能反映对应自变量的重要程度。这时的回归方程称为标准回归方程,回归系数称为标准回归系数,表示如下:
=·1+·2+…+·
3 线性回归分析在应用中的定量分析
以下定量分析是以某店铺2020年6—12月的投入产出数据为分析对象,运用线性回归分析的方法对某店铺的投入产出比(ROI)指数进行分析,并且建立预测模型进行短期预测。
3.1 数据初步分析
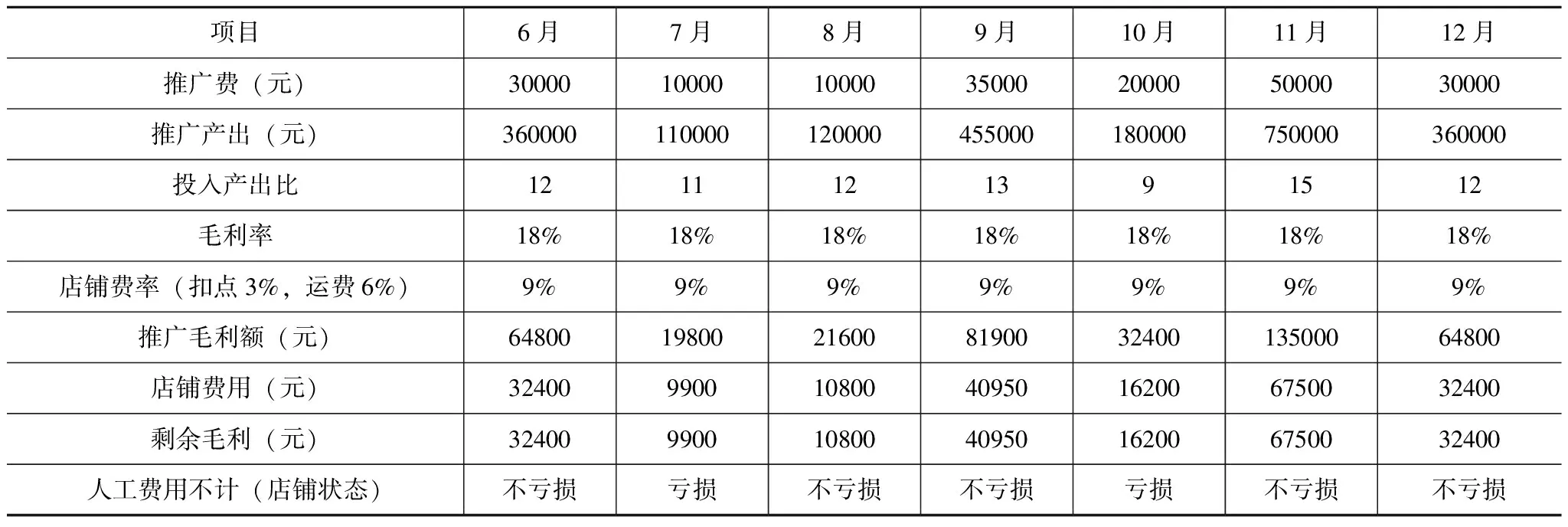
表1 某店铺2020年6—12月数据
假设,不存在异常数据(忽略淡季、旺季)情况下,根据上述数据,分析“推广费”数据后可以知道:
中位数:30000
众数:10000,30000
平均数:26428.57
分析“推广产出”数据后可以知道:
中位数:360000
众数:360000
平均数:333571.43
毛利率和店铺费率:稳定在18%,9%
推广毛利额=店铺费用+剩余毛利
人工费用不计的情况下,店铺状态:
剩余毛利无限趋近且大于推广费时,店铺是不亏损的。
剩余毛利小于推广费,店铺是亏损的。
根据投入产出比>12仍可推广的关系,得出9月、11月为可追加推广月份。
3.2 模型选择
根据上述数据分析,发现在毛利率和店铺费率不变的情况下:
投入产出比与推广产出、推广费有关系:
投入产出比ROI()=推广产出推广费
推广产出=×推广费+浮动系数
可以看出,推广产出只与推广费有关系,因此,选择一元线性回归分析模型。
推广产出=×推广费+浮动系数
=+
3.3 参数估计
使用一元线性回归要解决的问题——参数估计:投入产出比ROI()、浮动系数的估计;平方差的估计。
(1)投入产出比ROI()、浮动系数的估计(采用最小二乘法):
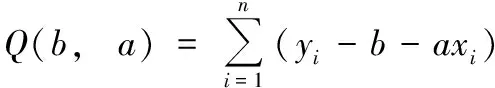
求估计,,使(,)最小。
,的最小二乘估计:

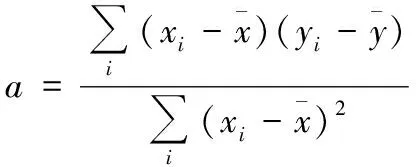
得到系数=155491,=-7736991855。
(2)方差的估计:
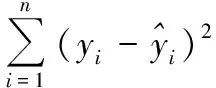
对于上述,所得回归方程及方差估计分别是:
回归方程:= 155491-7736991855
方差估计:=1994046243
3.4 模型检验
参数检验及模型应用:线性假设的显著性检验。根据上方数据分析得出推广产出散点图:

图1 推广产出
由图1可知,线性假设是显著的。
在此例中:
①散点图上几个点,几乎处在一条直线上,呈明显的线性关系;②在参数估计中,得出的一元线性回归方程(= 155491-7736991855)也表明:店铺数据呈线性相关关系;方程意义为:如果推广费平均每增加1元,推广产出平均增加15.5491元。
3.5 模型预测
根据上面得到的模型对某店铺 2021年1—5月的投入、产出、ROI进行短期预测,如表2所示。

表2
从表2可以看出:①在“投入产出系数”不变的情况下,“实际预测投入产出比”都在一定程度上无限接近12,整体预测是可信的,且对于店铺生产有指导意义。②从该模型的预测结果来看,1、2、4、5月的实际预测投入产出比均大于12,所以这几个月份是可以酌情继续追加推广费的;而3月11.68∝12,说明3月投放已经达到极限,不可追加推广,追加则亏损。
4 模型结论
①在数据预测中,ROI在一定限度上无限接近12,整体预测是可信的;②商家可以根据ROI预测值酌情增加、减少推广费(ROI>12,增加推广费;ROI<12,减少推广费,使ROI无限趋近12后停止减少);③从该模型的预测结果来看,模型的拟合效果较好,具有指导价值;④ROI指数在电商店铺中的应用是显著的,可以看出一段时间内的数据波动对未来时间的预测起到显著作用。所以线性回归分析在数据预测上具有应用价值,且易用性更高。
5 模型的不足
文章运用回归分析的方法对某店铺建立了一元线性回归模型,模型的预测效果相对较好,但是这个模型本身还有不足之处:①数据选择缺乏针对性:对于销售旺季、淡季等数据提炼,还需人为调整;忽略了大部分影响因素才促成了一元线性回归模型。②短期内数据预测模型较好,长期预测模型误差较大:数据序列的不断拉长,人工、毛利、店铺费用在实际应用中的作用开始显现,导致误差增大。③适用于短期内体量较大数据的分析,对于决策者和实施者都具有很好的指导意义,可以根据不同月份、不同情况调整投入金额,适当扩大市场。④由于世界环境变化,经济体系和市场分布变化,会导致供求关系转变,所以及时调整迅速梳理才是关键。

