关于新课标下复数教学的几点建议

单如恒

江苏省连云港高级中学 222000

高考对复数的考查要求并不高，往往是一个送分的选择题，主要考查复数的概念、复数的运算和复数的几何意义.基于此，教学中教师往往只对复数做应试层面的教学，而对复数的发展史、复数的内涵以及复数的应用涉及较少，这显然不符合当前提高学生数学核心素养的教学目标的要求［1］.那么，教师应如何教才能体现出新课标理念，才能为学生的终身发展服务呢？对此，笔者提出几点复数教学建议，与同人共探.

回顾复数历史，渗透数学文化

教数学，并非仅是教学生如何解题，还要让学生了解数学知识的发展历史.尤其是在“文化自信，以德树人”的背景下，教师应积极把“数学教学”转型为“数学教育”.基于此，复数教学，教师不能仅围绕高考去教，而应把复数当成真正的数学知识去教.

任何一个数学知识的形成都经历了历史的洗礼，复数也不例外.教学中教师应该让学生了解复数的发展历史，培养学生对数学的情感.什么是复数？复数是实数与虚数的统称.对于实数，学生在初中阶段已经学过，因此这里的焦点是虚数.虚数真的是虚无缥缈的数吗？教师可以带领学生回顾虚数形成的这段历史.在数学知识的发展史中，对虚数的假设是需要勇气的，因为当时人们都无法接受，认为虚数是想象出来的一种数，是不存在的，但数学家们还是对虚数进行了长期的研究.首次认真研究虚数的是意大利数学家卡丹（Cardano，1501—1576），他生活在文艺复兴时期，堪称数学“怪杰”，他从1545年开始研究虚数，当时他把虚数叫做“诡辩量”.大约过了100年，著名数学家笛卡尔将这种数命名为虚数.后来又过了140多年，大数学家欧拉还是认为它是虚幻之数，于是用英文单词imaginary（虚幻）的第一个字母i来表示它的单位，直到1831年大数学家高斯才对复平面作出了详细说明，让复数a+bi有了立足之地和用武之地，人们也才认识到复数.时至今日，复数在现代数学科技中有着广泛的应用，无论是流体力学、热力学、机翼理论，还是代数学、数论、微分方程，甚至是理论物理、弹性力学、天体力学，都能找到“复数”的身影.

数学课上讲复数的发展史，是对历史的尊重，也是提高学生数学素养的重要途径.也许有人认为，只需简单地讨论方程x2+1=0在实数范围内无解就可以轻松引入复数，但学生却不能了解“真实的复数”，往往会认为复数只是一个符号.由此可见，教学中数学文化的渗透是何等重要，它有利于学生树立正确的数学观，学会用发展的眼光看待数学.

厘清复数概念，提高探究能力

数学概念的学习过程，一般分为六个阶段——感知阶段、想象阶段、概括阶段、形成阶段、应用阶段和结构阶段，这六个阶段体现了人们对事物的认知规律，也是学生学习复数概念的基本过程.复数对于学生来说是一个全新的概念，引入这个概念，教师可以引导学生在某些数学神奇的现象中发现和总结规律.

比如在复数概念教学中，笔者提出以下问题：

若x1，x2是方程x2+x+1=0的两个根，则两根之和是多少？两根之积又是多少？

对于这个问题，部分学生往往不假思索，依据韦达定理马上得出了答案：x1+x2=-1，x1·x2=1.而一些善于思考的学生则质疑：这个方程连实数根都不存在，哪儿来的两根之和与两根之积？韦达定理成立的前提条件是什么呢？是方程一定要存在实数根吗？如果方程没有实数根，它依然成立吗？于是，笔者向学生提议：假如存在另外一种根（先不妨叫它为虚根），我们来验证韦达定理是否成立.学生根据一元二次方程的求根公式得x1=，x2=，经检验，依然满足韦达定理.但学生又产生了新的问题：如何求-3的算术平方根呢？笔者提示，假设i2=-1（i为虚数单位），问题即可迎刃而解.于是学生求得x1=，同时发现，方程x2+x+1=0虽然不存在实数根，但它存在虚根，这两个虚根同样满足韦达定理.笔者提示，这两个虚根其实就是两个虚数.于是，趁势引出复数a+bi（a，b∈R）的有关概念——什么是复数的实部和虚部，什么是实数，什么是虚数，什么是纯虚数，什么是复数，并分别探讨当a+bi（a，b∈R）为实数或纯虚数时实部与虚部满足的条件.

在探讨的过程中，学生提出了疑问：虚数到底存在不存在？如果存在，它表示什么呢？可见学生很想知道复数的几何意义.于是，笔者引出了复平面概念，指出a+bi（a，b∈R）表示的是复平面上的点（a，b），学生很快发现，实数表示的点在x轴上，纯虚数表示的点在y轴上，虚数表示的点在四个象限内.接着，笔者引导学生回头看的几何意义，学生发现这两个根表示的点都在以原点为圆心的单位圆上，可见“虚根不虚”.再接着，笔者要求学生在复数范围内解方程x3-1=0.由于上述问题的铺垫，学生很快解得方程的三个根，分别是1，和，并惊奇地发现这三个根表示的点刚好把以原点为圆心的单位圆三等分，于是又得到了两个非常有用的结论：若ω=-则有①ω2+ω+1=0；②ω3=1.

概念是数学学习的基础，概念的产生都有着丰富的背景.笔者认为，从具体的背景中引导学生探究数学概念，比教师和盘托出数学概念更有利于学生对数学概念的建构.对于复数的概念课，或许有些教师认为不要提及复数的几何意义，但笔者认为复数的几何意义与复数的概念密不可分，结合复数的几何意义看复数的概念比单纯研究复数的概念更有利于学生理解.

强化复数应用，提升数学素养

新课标对复数教学的要求虽然不高，考试也只是要求学生掌握复数的概念以及基本运算和几何意义的简单应用，一般不会涉及难题，但从培养学生的核心素养的角度来看，笔者认为复数教学不能仅以考试要求为原则，还应通过强化复数应用，提高学生的数学素养.尤其是教材的选学内容——复数的三角表示，为复数教学指明了方向［2］.虽然是选学内容，但它能沟通复数的几何意义与三角函数之间的联系，笔者认为不妨将它当成必学内容.

继平面向量后，复数帮我们建立了一座联系代数与几何的“桥梁”，教师可以通过这座“桥梁”，帮助学生沟通数学知识间的联系，引导学生建构独特的复数法.下面举例说明：

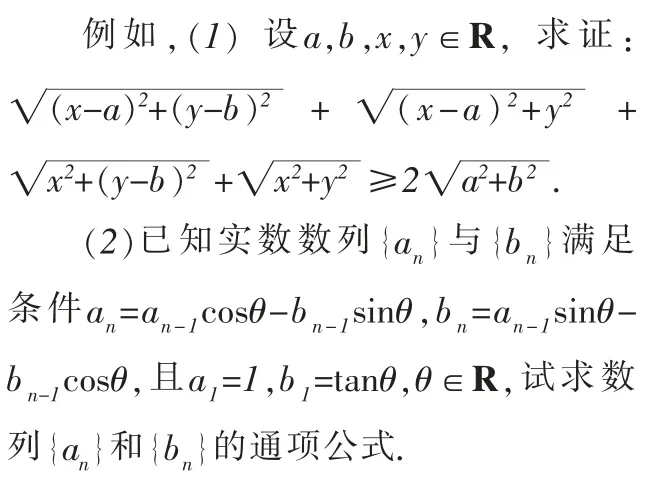
对于第（1）问，可以引导学生把每一个根号都看成复数的模，通过构造复数，利用复数的几何意义解决问题：

对于第（2）问，同样可以通过构造复数，利用复数的三角表示来解决数列问题：

由此可见，巧妙利用复数，可以创造性地解决一些比较复杂的问题，这些源于课本又高于课本的数学方法，也应该成为教学重点.虽然从应试角度来看，对复数方法拓展性的应用似乎没有必要，但从学生的终身发展来看，在复数教学中，这种数学思维的培养十分重要，也十分必要.因为无论学习什么，只有站得高才能看得远，“会当凌绝顶”，方可“一览众山小”.

以上三点建议，是基于学生的数学核心素养提出的，笔者认为，真正的数学教育应摆脱应试教育的束缚，走出“考什么，教什么”的误区.应忠于教材，又不囿于教材，以培养学生的关键能力，促进学生终身发展.