要素投入与生产效率对林业经济增长的非线性影响*——基于劳动报酬变迁视角

刘艳迪 张 滨 吕洁华

(1.东北林业大学经济管理学院 哈尔滨 150040； 2.河北师范大学商学院 石家庄 050024)

国有林区是我国重要的生态安全屏障和森林资源战略储备基地，在国家的经济社会发展和生态文明建设中发挥着重要作用。黑龙江省国有林区作为我国重点国有林区之一，在国家发展中同样扮演着关键角色。新中国成立之初，黑龙江省国有林区提供了全国近一半的木材产量1)(1)1)根据1949—1986年《中国林业年鉴》数据，1949年黑龙江木材产量269.3万立方米，全国木材产量567.0万立方米，黑龙江占全国木材产量的47.5%。，随着国有林区发展定位从以木材生产为主向提供生态产品和服务为主的转变，黑龙江省国有林区在保护生态环境和维持生态平衡方面发挥了不可替代的作用。习近平同志在党的十九大报告中强调，要坚持在经济增长的同时实现居民收入同步增长，在劳动生产率提高的同时实现劳动报酬同步提高。落实到黑龙江省国有林区，就是要实现林区职工劳动报酬与经济发展水平同步增长，将林区的经济增长问题与职工收入问题紧密联系在一起。为实现黑龙江省国有林区职工劳动报酬与林区经济水平的同步增长，厘清劳动报酬变迁在林业经济增长中的作用尤为关键。

学术界有关林业经济增长问题的研究大致分为两个方向： 一是关于林业经济增长影响因素的研究，主要包括林业要素投入(李研等，2018； 张滨等，2020)、技术进步(孔凡斌等，2014； 柯水发等，2014)、产权制度、产业结构(黄烈亚等，2008)、产业集聚(魏肖杰等，2018； 夏永红等，2019)、市场化进程(孔凡斌等，2013)等因素； 二是关于林业全要素生产率测度及其影响因素的研究，测度方法主要运用DEA- Malmquist 指数法(黄安胜等，2015； 姜钰等，2018)和SFA- Malmquist指数法(史常亮等，2017)，受林业产业集聚(魏肖杰等，2019)、国家财政支持(曹玉昆等，2020)等多种因素影响。虽然上述文献在很大程度上对研究林业经济增长问题提供了系列价值参考，但还存在一定的局限性，一方面大多数的研究假定各因素对林业经济增长的影响是线性的，而从现实情况来看，很多因素对林业经济增长的影响在不同阶段都存在差异，另一方面劳动报酬在经济分析中的作用不等同于劳动力，劳动报酬既来源于劳动成果，又反馈至生产过程，而基于劳动报酬变迁视角，系统分析劳动报酬变迁在林业经济增长过程中发挥的独特作用研究仍处空白。由于经济增长主要来源于两个方面： 一是生产要素投入量的增长，二是生产率的提高，因此本文旨在研究随着劳动报酬的变迁，林业要素投入与生产效率对林业经济增长的影响呈现怎样的非线性、阶段性特征，以及非线性结果产生的原因，系统阐述劳动报酬在林业经济增长中发挥的独特作用。

从劳动报酬的含义来看，“劳动报酬”与“工资”的含义相似，但比工资包含的范围更广，劳动报酬包含工资、奖金、津贴、福利和保险等(胡莹等，2019)，但由于非实物形式的福利等统计上存在困难，而工资是以货币形式直接支付给劳动者的劳动报酬，是劳动报酬中占比最重要的一部分，工资的高低直接反映着劳动报酬水平，因此在本文的分析中，用工资表征劳动报酬进行研究。关于劳动报酬与经济增长的关系方面，由于劳动者同时也是消费者，劳动报酬的增加，从劳动者角度出发，有利于鼓励劳动者勤勉，提高劳动生产率(刘丽等，2011)，能有效激励劳动者提高平均受教育年限，提升劳动者的技能水平(徐常建等，2019)，从消费者角度看，能有效促进居民消费(郑延智等，2012)，进而促进经济增长。而低劳动力价格抬高了企业采用先进技术设备的临界点，因为当劳动力价格低廉而先进的技术设备又需要花费大量的资金时，企业多倾向选择劳动密集型的传统生产模式(王佳菲，2010)，不利于社会经济发展。

从劳动报酬变迁对林业要素投入与生产效率的经济增长效应的影响机理来看，短期内林业要素投入量和要素结构发生变化，由于要素价值的货币化衡量(利息、工资、地租等)与要素之间的替代作用，会对林业劳动力工资即劳动报酬产生直接或间接影响(中介效应)，进而影响林业经济增长，而基于效率工资理论可知，生产效率的提升影响着劳动报酬水平的变化； 在劳动力冗余的条件下，基于边际报酬递减规律，林业劳动力的减少与现代化技术设备的应用，使得劳动生产效率提升，劳动报酬也不断增加，为了降低劳动力成本，资本、林地等要素投入也将不断增加以形成要素替代作用或与之形成更为匹配的要素结构，提升林业生产效率，即意味着劳动报酬的上涨，至少能够提升部分林业要素投入与生产效率的边际贡献率(调节效应)； 从长期来看，体制改革、分配制度、技术创新等也会以骤变的形式直接作用于劳动报酬水平和林业生产过程，因此，林业要素投入与生产效率对林业经济增长的影响会随劳动报酬的变迁呈现出非线性、阶段性特征(门槛效应)。

鉴于以上分析，本研究以黑龙江省国有林区40个林业局为研究对象，一方面基于门槛回归模型，分析随着劳动报酬的变迁，林业要素投入与生产效率对林业经济增长的非线性影响，阐述其表现的阶段性特征，另一方面基于中介效应与调节效应模型，对劳动报酬发挥的具体作用进行解析，创新性地运用门槛、中介和调节效应模型展开实证分析，突显劳动报酬变迁在林业经济增长过程中存在的多种效应，从劳动报酬变迁视角解析林业经济增长过程中存在的内在逻辑机理与因果关系

1 研究方法、模型设定与数据来源

1.1 研究方法

1.1.1 面板门槛回归模型 Hansen(1999)提出了一种解决非线性问题的“非动态面板门槛模型”，其单一门槛回归方程如下：

(1)

式中：yit为被解释变量，xit为k维解释变量向量，qit为门槛变量(可以是解释变量的一部分)，其中i为地区变量，t为时间变量，I(·)为指示函数，当满足括号内条件时取1，不满足时取0，β1、β2为k维解释变量系数向量，γ为门槛值，ui为个体效应，εit为随机误差，服从均值为0，方差为σ2的独立同分布。

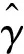
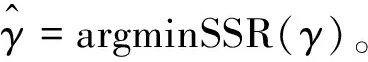
(2)

2)门槛效应检验。原假设为H0：β1=β2，构造似然比统计量

(3)

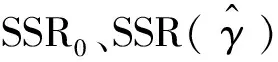
双重门槛回归方程如下：

(4)

同理，双重门槛回归模型也要进行门槛值估计和门槛效应检验，原理同上，不再赘述。

1.1.2 中介效应模型 考虑变量X对变量Y的影响，若X通过影响变量M来影响Y，则称变量M为中介变量(温忠麟等，2005)。中介效应的公式如下：

Y=cX+e1；

(5)

M=aX+e2；

(6)

Y=c′X+bM+e3。

(7)

式中，c为X对Y的总效应，a、b是经过中介变量M的中介效应，c’是直接效应，满足c=c’+ab。温忠麟等(2004)在总结各种检验方法的基础上，提出了一个中介效应检验程序，在学术届广为应用。该检验程序为：

1)检验回归系数c，若显著，进行第2)步；否则，停止中介效应检验。

2)依次检验回归系数a、b，若都显著，说明中介效应显著，进行第3)步；若至少一个系数不显著，还不能下结论，需要进行Sobel检验，进入第4)步。

3)检验系数c’，若显著，说明是部分中介过程，即X对Y的影响只有一部分是通过M来实现的；若不显著，说明是完全中介过程，即X对Y的影响都是通过M来实现的。检验结束。

4)进行Sobel检验，若显著，说明中介效应显著；否则，中介效应不显著。检验结束。

1.1.3 调节效应模型 如果变量Y与变量X之间的关系是关于变量M的函数，则称变量M为调节变量(温忠麟等，2005)。调节效应的原理如下：

假设Y与X的关系为

Y=aX+bM+cXM+e，

(8)

可以把式(8)改写为

Y=bM+(a+cM)X+e。

(9)

式(9)中，Y与X的关系由a+cM来表示，它是关于M的线性函数，c衡量了调节效应的大小。

当解释变量和调节变量均为连续型变量时，做Y关于XM的回归系数(系数c)检验，若显著，则调节效应显著。当X对Y的直接效应(系数a)显著为正时，若交叉项XM的系数(系数c)为正，说明调节变量M强化了X对Y的正向影响，表明M在X对Y的影响中起正向强化作用；若交叉项XM的系数为负，说明调节变量M弱化了X对Y的正向影响，M在X对Y的影响中起正向弱化作用。同理可知，当X对Y的直接效应显著为负时，若交叉项XM的系数为正，说明M在X对Y的影响中起负向弱化作用；若交叉项XM的系数为负，说明M在X对Y的影响中起负向强化作用。

1.2 指标选取与模型设定

1.2.1 指标选取 1)被解释变量：林业经济增长(Y)，用林业经济总产值(万元)表示。

2)核心解释变量与控制变量：林业资本投入(K)，用林业投资完成额(万元)表示(2)1)由于统计口径的变化，2003—2010年黑龙江省国有林区的林业投资完成额数值缺失，对此利用2011—2018年该地区40个林业局的林业投资完成额与林业固定资产投资完成额的平均比例数值，将2003—2010年林业固定资产投资完成额乘以平均比例系数1.517 9后的数值代替其林业投资完成额数值进行后续分析。1)；林业劳动力投入(L)，用在岗职工年平均人数(人)表示；林地投入(F)，用森林面积(hm2)表示；林业生产效率(TFP)，用林业全要素生产率(以上一年效率值为1)表示，本文中的林业全要素生产率通过投入导向的、可变规模报酬的DEA-Malmquist指数法计算得到，其中投入变量为K、L、F，产出变量为Y。在本文的研究中，4个解释变量依次作为核心解释变量进行建模，其余解释变量则作为控制变量。

3)门槛、中介与调节变量：劳动报酬(W)，用在岗职工年平均工资(元)表示。

1.2.2 面板门槛回归模型设定 本文旨在研究在劳动报酬不断变化的前提条件下，林业要素投入与生产效率对林业经济增长的非线性影响情况，因此把劳动报酬设定为门槛变量，分别分析林业资本投入、林业劳动力投入、林地投入、林业生产效率对林业经济增长影响的阶段变化特征。下面以林业资本投入对林业经济增长的影响为例，根据门槛效应的检验结果，构建模型(10)或(11)(3)2)检验结果为单一门槛时，构建模型(10)；为双重门槛时，则构建模型(11)。其余解释变量对林业经济增长的影响模型构建原则与此相同。2)：

LNYit=α0+α1LNKit(LNW≤γ)+

α2LNKit(LNW>γ)+β1LNLit+

β2LNFit+β3TFPit+εit；

(10)

LNYit=α0+α1LNKit(LNW≤γ1)+

α2LNKit(γ1γ2)+

β1LNLit+β2LNFit+β3TFPit+εit。

(11)

式中：α0为待估计常数项，α1、α2、α3为待估计门槛系数，β1、β2、β3为待估计控制变量系数，εit为随机误差项。

1.2.3 中介效应模型设定 面板门槛模型的回归结果能够证明劳动报酬变迁视角下林业要素投入与生产效率对林业经济增长存在非线性影响，并不能指明劳动报酬在其中具体发挥怎样的作用，因此，需要进一步运用中介效应和调节效应模型将劳动报酬作为第三方变量，具体分析劳动报酬的潜在作用以及导致林业经济存在非线性增长的原因。这里的中介效应模型主要用于分析劳动报酬在林业要素投入与生产效率对林业经济增长的影响中是否发挥中介效应，以及发挥怎样的中介效应(完全中介或部分中介)等。本文对劳动报酬的中介效应分析针对模型(12)～(14)展开：

LNYit=α0+α1LNKit+α2LNLit+α3LNFit+

α4TFPit+εit；

(12)

LNWit=β0+β1LNKit+β2LNLit+β3LNFit+

β4TFPit+μit；

(13)

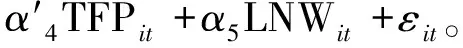
(14)

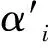
1.2.4 调节效应模型设定 调节效应模型主要用于进一步分析劳动报酬在林业要素投入与生产效率对林业经济增长的影响中发挥的调节效应情况，包括在具体哪些因素对林业经济增长的影响中发挥调节效应(是或否)，以及发挥怎样的调节效应(正向强化、正向弱化、负向强化、负向弱化)等，定性分析调节效应的大小(4)3)由于模型(15)～(18)中的解释变量与调节变量需要中心化处理(温忠麟等，2005)，因此分析调节系数的大小意义不大，仅能定性分析调节效应的正负情况。3)。本文对劳动报酬的调节效应分析针对模型(15)～(18)展开：

LNYit=α0+α1LNKit+α2LNLit+α3LNFit+

α4TFPit+α5LNWit+β1LNKit*LNWit+εit；

(15)

LNYit=α0+α1LNKit+α2LNLit+α3LNFit+

α4TFPit+α5LNWit+β2LNLit*LNWit+εit；

(16)

LNYit=α0+α1LNKit+α2LNLit+α3LNFit+

α4TFPit+α5LNWit+β3LNFit*LNWit+εit；

(17)

LNYit=α0+α1LNKit+α2LNLit+α3LNFit+

α4TFPit+α5LNWit+β4TFPit*LNWit+εit。

(18)

式中：α0为待估计常数项，αi为待估计解释变量系数，βi为调节效应系数，εit为随机误差项。

1.3 数据来源

本文研究数据由2003—2017年《中国林业统计年鉴》、2018年《中国林业和草原统计年鉴》以及龙江森工集团内部统计资料(包括森林资源二类调查数据)整理得到。其中，林业经济增长(Y)、林业资本投入(K)以及劳动报酬(W)变量数值用以2003年为基期的CPI进行平减处理以剔除物价影响，并对部分变量数值进行对数化处理。本研究的样本单位为黑龙江省国有林区40个林业局，样本期为16年，共计640个样本量。变量描述性统计见表1。

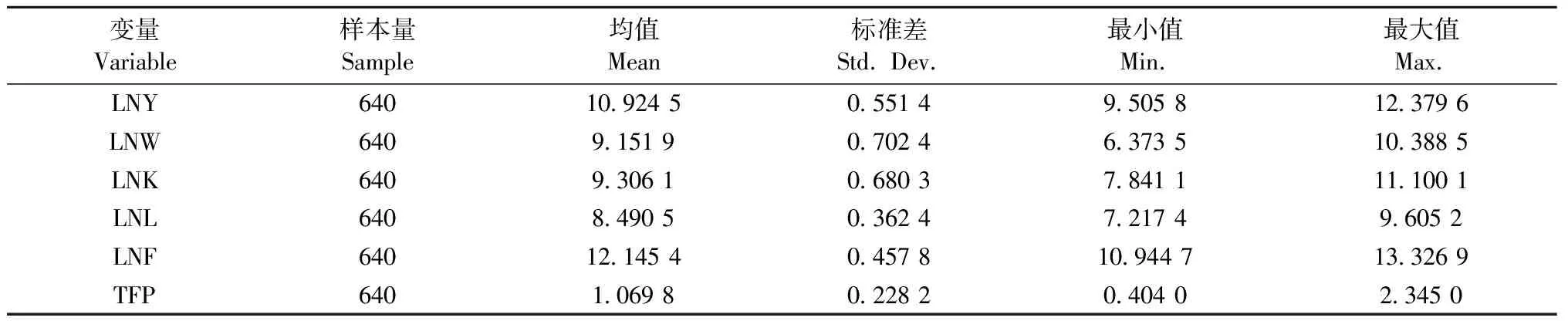
表1 变量的描述性统计①Tab.1 Descriptive statistics of variables

2 结果与分析

2.1 门槛效应结果与分析

2.1.1 门槛值确定及门槛效应检验 运用StataSE15.1软件，以LNW为门槛变量，建立不同解释变量(LNK、LNL、LNF、TFP)的门槛效应模型，确定不同解释变量的门槛类型及门槛值，结果见表2。

结果显示，对林业资本投入、林业劳动力投入、林地投入、林业生产效率4个变量而言，其对林业经济增长的影响因劳动报酬变迁而存在双重门槛效应，且均在1%的显著性水平下通过检验。其中，林业资本投入的劳动报酬门槛值为9.03和9.81，林业劳动力投入和林地投入的劳动报酬门槛值为9.17和9.81，林业生产效率的劳动报酬门槛值为9.17和9.83。

2.1.2 门槛回归结果与分析 根据不同解释变量的门槛类型结果，分别建立以LNW为门槛变量的门槛回归模型(模型2～5)，并与未加入门槛变量的普通面板回归模型(模型1)结果对比，整理后结果见表3。

从门槛回归模型与普通面板回归模型的结果对比来看，门槛回归模型的拟合优度R2值和方程的F统计量均更高，对回归方程拟合的更好，而从门槛回归模型的系数显著性来看，林业要素投入与生产效率的回归系数(包括门槛系数)均在5%的显著性水平下通过检验，回归方程在1%的显著性水平下也均通过了F检验，因此门槛回归模型能更好地解释变量之间的关系，比普通面板回归模型更具代表性。

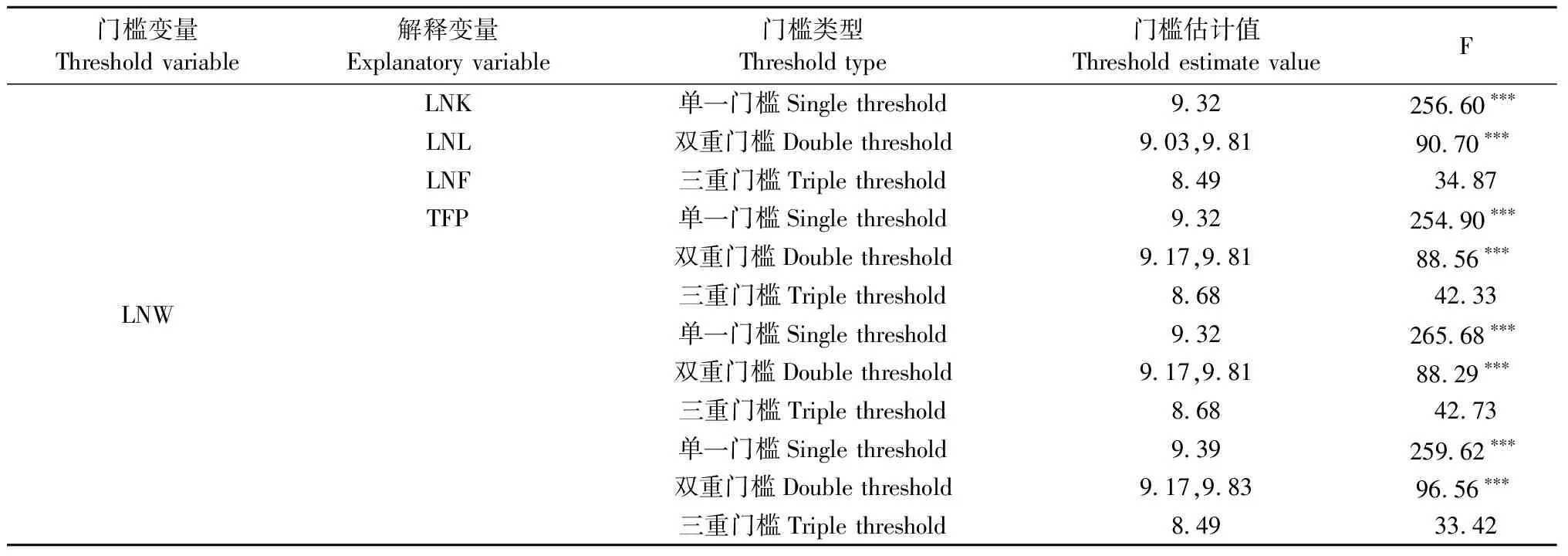
表2 门槛个数及门槛值确定①Tab.2 Threshold number and threshold value determination

表3 门槛回归模型结果①Tab.3 Threshold regression model results

通过模型2～5中门槛值前后的回归系数对比，可以看出，劳动报酬越过门槛值前后，林业资本投入、林业劳动力投入、林地投入、林业生产效率等因素对林业经济增长的弹性和半弹性系数均发生阶段性变化，且呈现显著的上升趋势，整体表现为非线性的影响特征。以模型2为例，林业资本投入对林业经济增长的影响不是一成不变的，而是表现出阶段性变化特征，当劳动报酬未越过第一个门槛值时，林业资本投入对林业经济增长的弹性系数为0.245 4，此时林业资本投入每增加1%，平均带动林业经济增长0.245 4%； 当劳动报酬越过第一个门槛值而未越过第二个门槛值时，林业资本投入对林业经济增长的弹性系数上升为0.274 8，此时林业资本投入每增加1%，平均带动林业经济增长0.274 8%； 当劳动报酬越过第二个门槛值后，林业资本投入对林业经济增长的弹性系数再次上升为0.305 4，此时林业资本投入每增加1%，平均带动林业经济增长0.305 4%。研究结果表明： 林业要素投入与生产效率对林业经济增长的影响受到劳动报酬水平的制约，只有劳动报酬达到一定的水平，才能有效激发林业要素投入与生产效率的经济增长效应，提高林业要素投入与生产效率的边际产出。

出现这种结果的原因是，对企业来说，当职工劳动报酬水平过低时，林业企业依靠廉价劳动力也能赚取利润，影响了林业资本与技术对劳动力的正常替代，企业没有动力通过改变要素配置、升级更新设备、加大研发投入等举措提高生产效率，因而过低的劳动报酬水平阻碍了林业产业结构升级和林业经济发展，只有当劳动报酬水平越过一定的门槛值时，企业才有动力提升效率以应对工资上涨； 对职工来说，当劳动报酬低于门槛值时，职工倾向于选择怠工，只有劳动报酬高于门槛值时，职工才会努力工作以提升劳动生产率。

2.2 中介效应结果与分析

中介效应模型回归结果见表4。可以看出，林业要素投入与生产效率对林业经济增长影响的总效应(模型1中的各变量系数)在1%的显著性水平下均通过检验； 把劳动报酬作为中介变量时，各变量对劳动报酬的影响系数在1%的显著性水平下也均通过检验； 劳动报酬对林业经济增长的影响系数在1%的显著性水平下也通过检验。表明劳动报酬在林业要素投入与生产效率对林业经济增长影响的过程中发挥着显著的中介效应。

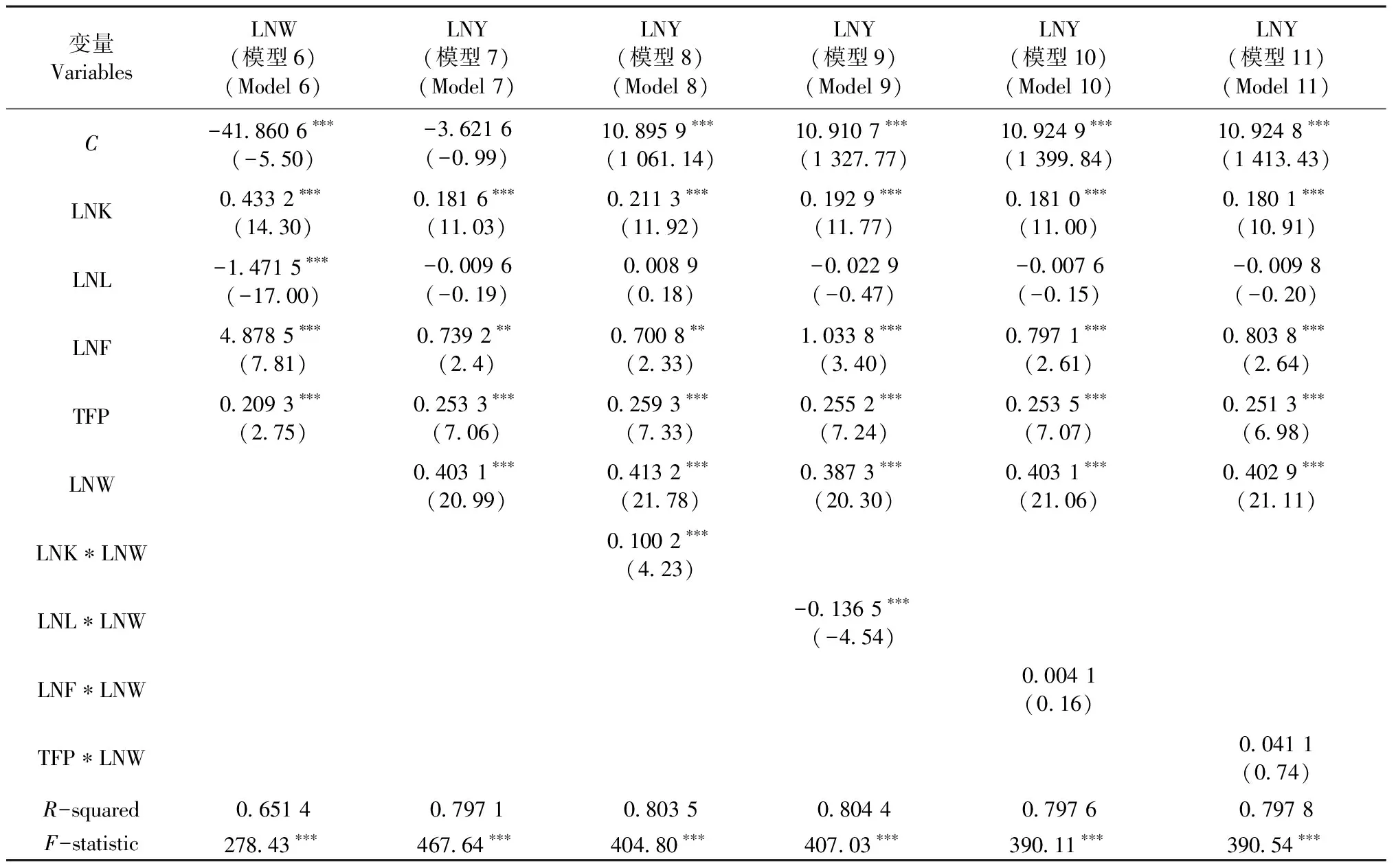
表4 中介效应和调节效应模型回归结果①Tab.4 Regression results of mediating effect and moderating effect model

具体来看，林业资本投入对林业经济增长的总效应为0.356 2，其中直接效应为0.181 6，通过劳动报酬影响的中介效应为0.174 6(0.403 1×0.433 2)，中介效应占总效应比重49.02%，且系数在1%的水平下均显著，劳动报酬发挥部分中介效应； 林业劳动力投入、林地投入与林业生产效率对林业经济增长的中介效应分析与上述类似，这里不再赘述，汇总后的劳动报酬在各变量对林业经济增长影响中的中介效应情况见表5。

上述结果表明，林业要素投入和林业生产效率会通过影响劳动报酬水平，进而影响林业经济增长。从林业要素投入来看，当林业资本和林地投入量发生变化时，由于要素供求关系的变化，会直接引起要素价格(利息、地租)发生改变，基于要素间的替代作用，会间接引起劳动力工资即劳动报酬发生改变，当林业劳动力投入量发生改变时，则会直接引致劳动报酬的改变，劳动报酬的不断提升，有利于增加林产品消费、改善林产品需求结构、促进林业产业升级，进而引起林业经济增长。从林业生产效率来看，由效率工资理论可知，工资水平与生产率之间存在双向的作用机制，林业生产效率的提升，会引致职工劳动报酬增加，进而促进林业经济增长。

表5 变量中介效应汇总①Tab.5 Summary of mediating effect of variables

此外，从林业要素投入与生产效率通过劳动报酬影响林业经济增长的实际效果来看，林业要素投入与生产效率的年平均增长率分别为林业资本投入8.108%、林业劳动力投入-3.427%、林地投入0.270%、林业全要素生产率4.888%，相应引起的林业经济年平均增长分别为2.888%、2.066%、0.730%、0.017%，合计5.701%； 其中，各变量通过劳动报酬中介变量引起的林业经济年均增长分别为1.416%、2.033%、0.531%、0.004%，合计3.984%。由此可知，各变量的经济增长效应共有69.88%是通过劳动报酬中介变量实现的，劳动报酬变迁在要素投入和生产效率对林业经济增长的影响过程中存在决定性作用。

2.3 调节效应结果与分析

调节效应模型回归结果见表4。可以看出，加入解释变量与调节变量的交互项后，仅LNK*LNW和LNL*LNW的回归系数在1%的显著性水平下通过检验，而LNF*LNW和TFP*LNW的回归系数未通过检验，说明劳动报酬在林业资本投入和劳动力投入对林业经济增长的影响中发挥显著的调节效应，而在林地投入和林业生产效率对林业经济增长的影响中不发挥调节效应。

具体来看，在模型8中，LNK的回归系数值为0.211 3，说明在平均劳动报酬水平下，林业资本投入每增加1%，平均引起林业经济增长0.211 3%，LNK*LNW的回归系数值为正值，则说明当林业资本投入不变时，随着劳动报酬的增加，林业资本投入对林业经济增长的边际产出会更高，劳动报酬会正向强化林业资本投入对经济增长的影响。在模型9中，LNL的回归系数值为-0.022 9，这不代表在平均劳动报酬水平下，增加林业劳动力投入会导致林业经济增长下降，而是说明林业劳动力已达到饱和状态，林区仍有大量的冗余职工，提高劳动报酬会降低就业水平，LNL*LNW的回归系数为负值，则说明当劳动报酬增加时，会负向强化林业劳动力投入对经济增长的影响，造成更多的职工富余，相同的林业经济产出仅需更少的林业劳动力投入就能得到，劳动报酬发挥负向强化的调节效应。而在模型10和11的林地投入与林业生产效率对经济增长的影响中，劳动报酬同样显示为正向强化的调节效应，但在统计上不显著。

出现这种结果的原因在于，随着劳动报酬的增加，从企业层面来看，林业企业会更加注重技术创新，同样的资本投入，会优先分配在相对技术密集型产业部门，提升林业资本的边际产出，从劳动者层面看，林业劳动者也会有动力和能力进行创新，提高个人在教育、培训等方面的支出，提升自身的技能水平，实现收入和自我价值的提升； 而工资水平较低时，企业和劳动者都没有动力进行技术的改进和个人能力的提升。

综合本文的研究结果如下：

1)林业要素投入与生产效率对林业经济增长的影响均存在基于劳动报酬变迁的双重门槛效应，且在跨越不同门槛值后，影响程度较前一门槛区间均有不同程度的提升。说明林业要素投入与生产效率对林业经济增长的影响受到劳动报酬水平的制约，当劳动报酬水平达到不同的阶段时，激发的林业要素投入与生产效率的经济增长效应不同，从而导致相同的林业要素投入与生产效率带来的边际产出也存在差异。

2)劳动报酬在林业要素投入与生产效率对林业经济增长的影响中发挥显著的中介效应，其中在林业资本投入、林地投入、林业生产效率对林业经济增长的影响中发挥部分中介效应，而在林业劳动力投入对林业经济增长的影响中发挥完全中介效应，按中介效应大小顺序排列为林业劳动力投入(98.42%)>林地投入(72.68%)>林业资本投入(49.02%)>林业生产效率(24.99%)，林业要素投入与生产效率对林业经济增长的影响有69.88%是通过影响劳动报酬来实现的，劳动报酬提升在要素投入增加与生产效率提升促进林业经济增长的过程中是极为重要且必不可少的环节。

3)劳动报酬在林业要素投入与生产效率对林业经济增长的影响中发挥部分调节效应，其中在林业资本投入对林业经济增长的影响中发挥正向强化的调节效应，在林业劳动力投入对林业经济增长的影响中发挥负向强化的调节效应，而在林地投入与林业生产效率对林业经济增长的影响方面调节效应不显著。说明林业资本与劳动力投入对林业经济增长的边际效应不是一成不变的，随着劳动报酬的提升而不断增强。

3 结论

综合来看，考虑到劳动报酬变迁的影响，林业要素投入与生产效率对林业经济增长的影响是非线性的，这是劳动报酬在林业要素投入与生产效率对林业经济增长影响中长期发挥门槛、中介、调节及其他多种效应综合作用的结果，劳动报酬提高与林业经济增长之间存在内在一致性与深层次因果关系。因此，对黑龙江省国有林区来说，提升林区职工工资水平，完善职工岗位奖励机制，有利于实现林区职工劳动报酬与林区经济水平的同步增长。