一种双裕度旋转变压器的优化设计及仿真分析

王永博，李长年，许兴斗，周奇慧，周竞捷

(中国电子科技集团公司第二十一研究所，上海 200233)

0 引 言

旋转变压器作为角度传感器，具有精度高、可靠性高、环境适应性强等特点，广泛应用于军工、航空、航天、汽车等场合[1]。双裕度旋转变压器将两套旋转变压器集合为一体，两套旋转变压器均可以独立工作，进一步提高了整个产品的可靠性。

在某些特殊场合下，双裕度旋转变压器中的两套旋转变压器需要同时工作，分别与两套上位机系统进行交互，并同时将机构的旋转角度进行输出。

本文针对某一种双裕度旋转变压器(以下简称旋变)进行研究，该双裕度旋变由两套无刷旋变组成并同时工作，应用场路耦合的方法对其结构尺寸及结构布局进行优化，并完成实验验证。

1 工作原理

双裕度旋变的结构图如图1所示，内部两套旋变均为无刷结构，无刷旋变A和无刷旋变B集合为一体。无刷旋变A组成部分包括：旋变A定子、旋变A转子、环变A定子和环变A转子；无刷旋变B组成部分包括：旋变B定子、旋变B转子、环变B定子和环变B转子。

图1 双裕度旋变结构图

无刷旋变A和无刷旋变B的工作原理相同，以无刷旋变A为例说明。环变A定子绕组激磁，通过电磁感应在环变A转子绕组中生成电信号，环变A转子绕组通过短接将电信号传递给旋变A转子绕组，再通过电磁感应在旋变A定子绕组中产生两路正交的电信号，两路信号与转子转角成正余弦关系，分别为正弦输出信号和余弦输出信号。将两路信号进行处理即可以得到转子转角，用来指示转角位置[2]。

双裕度旋变的电压方程式如下。

无刷旋变A：

UA_EXC=Usin(ωt)

UA_SIN=KUsin(ωt)sinθ

UA_COS=KUsin(ωt)cosθ

无刷旋变B：

UB_EXC=Usin(ωt)

UB_SIN=KUsin(ωt)sinθ

UB_COS=KUsin(ωt)cosθ

式中:两套无刷旋变以下标A和B区分，UEXC表示激磁电压，USIN表示正弦输出电压，UCOS表示余弦输出电压；U为激磁电压有效值;K为变压比;ω为激磁频率;θ为转子转角。

双裕度旋变电气原理图如图2所示。

图2 双裕度旋变电气原理图

2 磁路法确定初步方案

通过磁路法将磁路等效成磁阻，可将求解磁场问题简化成求解磁路的问题，快速计算出电磁方案。双裕度旋变中的两套无刷旋变电磁方案相同，结构设计相同。

无刷旋变磁路法的求解过程：以主要技术指标作为目标参数，以尺寸参数和绕组参数作为计算输入，结合公式及磁化曲线、损耗曲线查表，完成磁路、损耗的计算与迭代，使饱和系数和电势系数误差最小，最后再校核计算输出是否满足主要技术指标[3]。

计算流程图如图3所示。

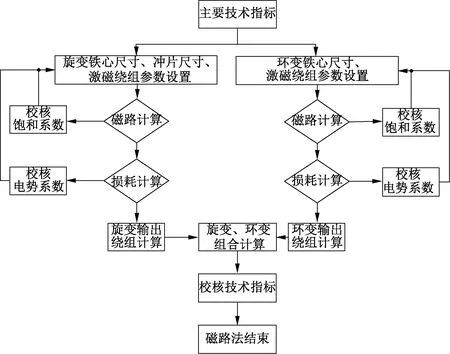
图3 磁路法计算流程

用在特殊场合的此种双裕度旋变，安装后会存在±0.3 mm的轴向窜动量，为满足实际使用要求，旋变定子铁心厚度和环变铁心齿厚度应预留0.6 mm的余量。通过磁路法计算，各铁心尺寸主要设计参数如表1所示。

表1 初步设计参数

3 有限元优化设计

磁路法无法准确模拟真实的磁场，在对双裕度旋变轴向尺寸优化时，无法准确反映优化前后的差异。另外，此种双裕度旋变的工作模式较为特殊，两套无刷旋变需要同时工作，在此情况下，两套无刷旋变的磁场将会相互影响，传统的磁路法已无法求解这种磁场。

为了解决以上问题，可以采用有限元法对电磁场计算，将求解场的微分问题转换为各剖分网格下泛函求极值的问题，更为准确地计算出电磁场。本文采用有限元仿真软件Maxwell对双裕度旋变完成两方面的优化：轴向尺寸的优化设计；两套无刷旋变的合理布局。

3.1 轴向尺寸的优化

将环变定子侧激磁作为原方，环变转子侧感应电信号作为副方。图1中，环变铁心内部中间为环形槽，其中放置线圈；两侧的轴向铁心部分为环变的齿部，主要起导磁作用。

在对轴向尺寸进行优化时，应保证双裕度旋变仍满足在轴向窜动中使用的要求。图4为轴向尺寸优化前后的对比。图4中，优化前为磁路法计算出的方案，L为无刷旋变的轴向长度，轴向尺寸X等于轴向窜动量(±0.3 mm)。

轴向尺寸的优化方法为环变原(副)方两侧齿部厚度不等，而初步方案中原(副)方两侧齿部厚度是相等的。

图4 优化前后轴向长度对比

图4中，优化后的环变定子铁心两侧齿部厚度不等，轴向长度相差2X；环变转子铁心两侧齿部厚度也不等，轴向长度也相差2X。环变定子的大齿对应环变转子的小齿，环变定子的小齿对应环变转子的大齿。这种环变原(副)方两侧齿部厚度不等的结构使得单个无刷旋变轴向长度为L-2X，轴向长度减小2X，双裕度旋变将减小轴向长度4X。

环变原(副)方两侧齿部厚度不等，则环变磁场将不再对称。下面应用有限元法计算采用该结构是否仍能满足性能要求。

优化前和优化后的磁力线图如图5所示。从图5中可以看出,磁路主要路径均为环变定子齿和转子齿，优化前有一部分漏磁路不经过环变转子齿，由于匝链环变转子绕组的磁链减少，故优化前的感应电动势将比优化后的感应电动势稍小一些。

图5 优化前后磁力线图

优化前和优化后的磁密云图如图6所示。优化前后铁心中各部位磁密饱和程度基本一致。

图6 优化前后磁密云图

计算优化前后环变的输出电压，如表2所示。从表2中可知，在不同位置的输出电压变化率优化后高于优化前，但变化率仅为0.35%，远小于实际使用中小于等于10%的要求。

由以上有限元计算结果可知，环变原(副)方两侧齿部厚度不等的结构(即优化方案)可以减少双裕度旋变的轴向长度，而对于环变的输出电压则没有影响。

表2 优化前后输出电压对比

3.2 内部布局的优选

3.2.1 两种布局的对比

双裕度旋变中两套无刷旋变同时工作，两套无刷旋变产生的磁场将会相互影响，这种影响会反映到无刷旋变的输出角度中。双裕度旋变按照环变与旋变的相对位置关系，可分为非对称排布和对称排布，即两种布局方式：环变A—旋变A—环变B—旋变B(第一种布局)，旋变A—环变A—环变B—旋变B(第二种布局)，两种布局如图7所示。

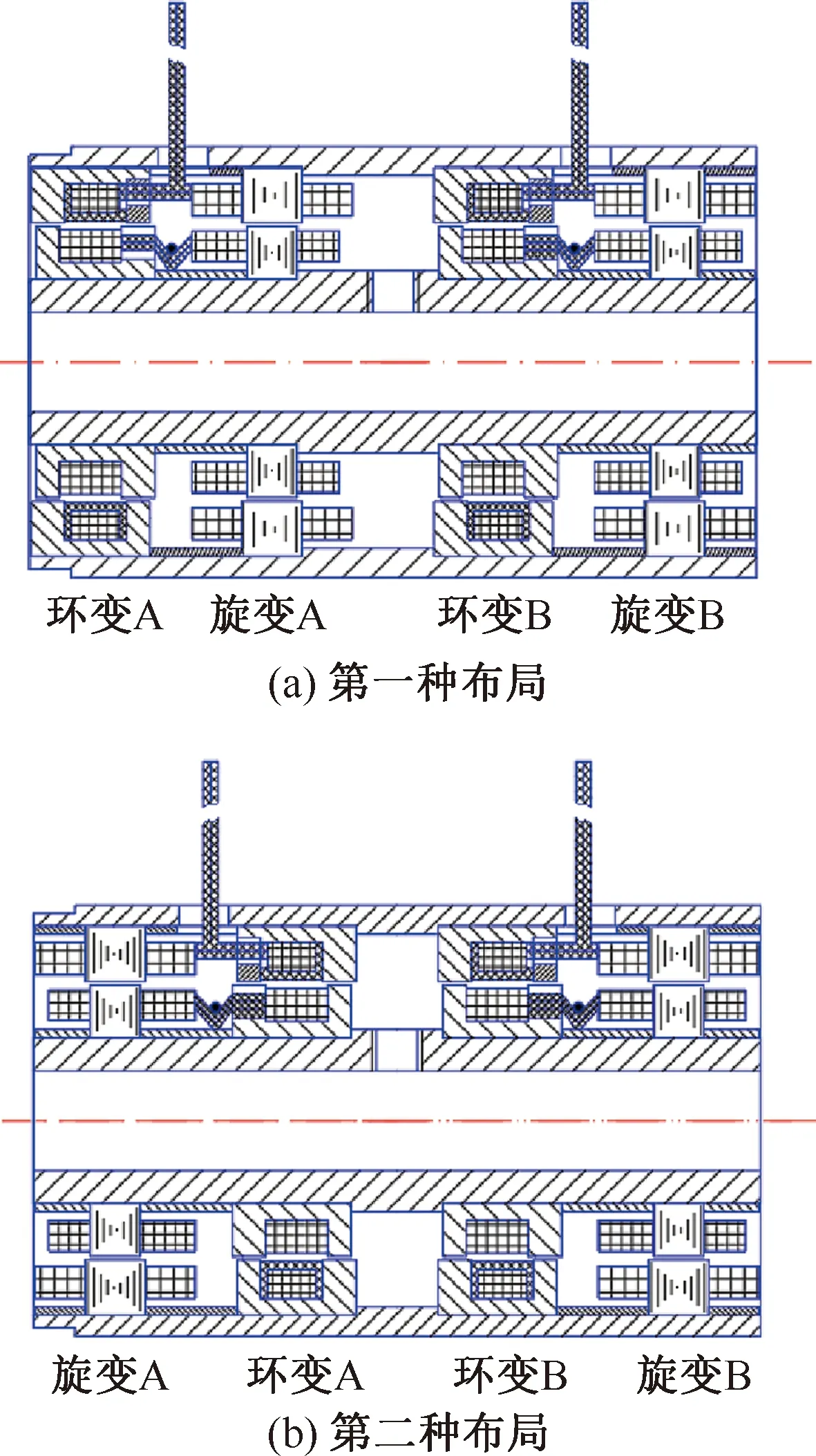
图7 两种布局方式

应用有限元法计算两种布局方式下，两套无刷旋变各自在不同转子位置下的正弦输出电压和余弦输出电压，再经过解算算法计算，可以求得两套无刷旋变各自的解算角度。通过对比可知，两套无刷旋变同时工作时，相互作用的磁场对两种布局的影响程度是不同的，影响较小的一种布局方式更合理。

求解无刷旋变解算角度的计算框图如图8所示。

图8 解算角度计算框图

两种布局方式分别建立三维模型，(如图9、图10所示),应用有限元仿真软件计算两套无刷旋变同时工作,转子在不同位置下的正弦及余弦输出电压，并通过解算算法计算出无刷旋变输出角度。

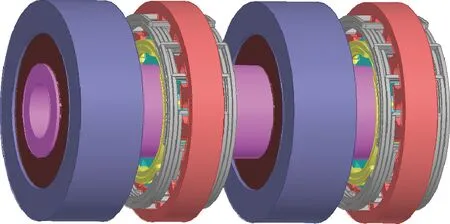
图9 第一种布局(隐藏机壳)

图10 第二种布局(隐藏机壳)

第一种布局下，无刷旋变A和无刷旋变B同时工作时，选取转子6个位置(0°、30°、60°、90°、180°和270°),计算无刷旋变A的正余弦输出电压和无刷旋变B的正余弦输出电压，并将计算结果进行解算，得到无刷旋变A和无刷旋变B同时工作时转子在各个位置下输出角度值。

实际应用中，无刷旋变A和无刷旋变B将输出角度分别传输给两套上位机系统，两者的角度偏差越小，两套系统接收到的转角位置越一致，后续机构执行动作越准确。

第一种布局下，无刷旋变A和无刷旋变B在各位置下输出角度值及角度偏差，如表3所示。

第二种布局下，无刷旋变A和无刷旋变B同时工作时，选取转子相同的6个位置,计算无刷旋变A的正余弦输出电压和无刷旋变B的正余弦输出电压，并将计算结果进行解算，得到无刷旋变A和无刷旋变B同时工作时，转子在各个位置下输出角度值及角度偏差，如表4所示。

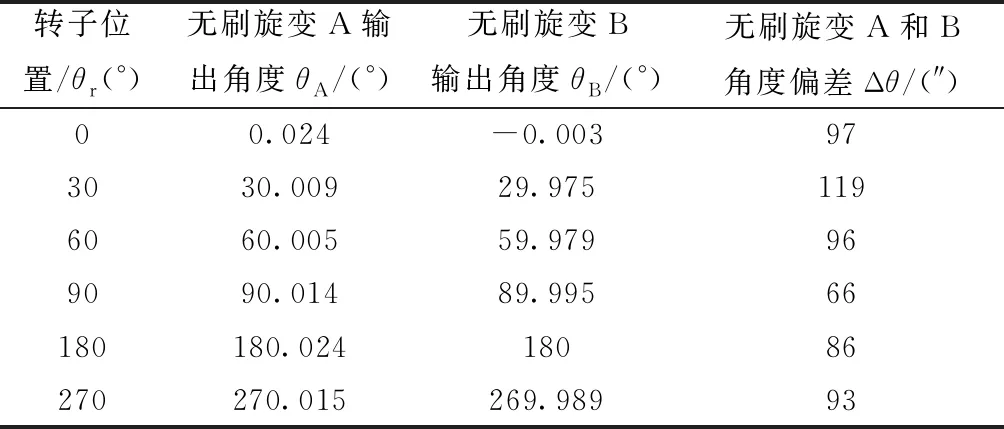
表3 第一种布局下角度偏差

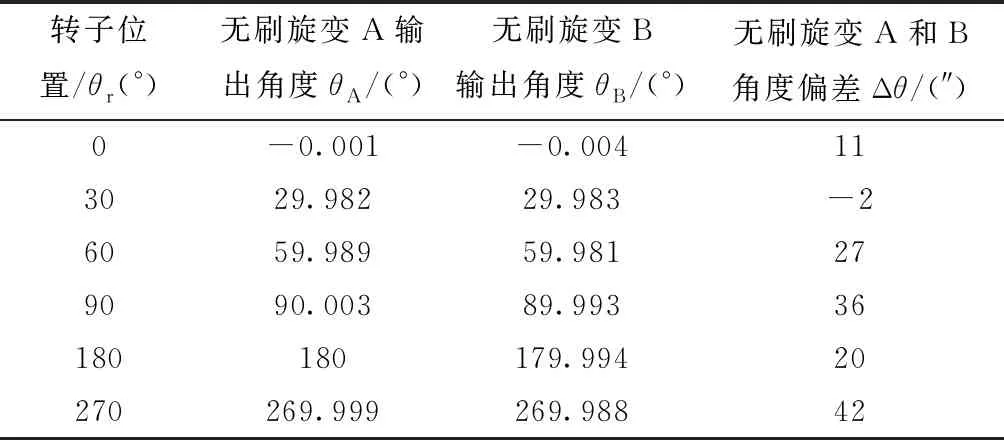
表4 第二种布局下角度偏差

通过表3和表4对比两种布局下无刷旋变A和无刷旋变B的角度偏差，第二种布局角度偏差最大为36″，而第一种布局角度偏差最大为119″，第二种布局下的角度偏差明显较小，说明第二种布局下两套无刷旋变的相互影响较小，第二种布局更为合理。

由无刷旋变输出角度进一步计算，可以求得无刷旋变在该位置的误差值。两种布局下，无刷旋变A和无刷旋变B在各个位置下的误差值如表5、表6所示。

表5 第一种布局下的角度偏差

表6 第二种布局下的角度偏差

对比表5和表6，无刷旋变A在第二种布局下的最大误差值65″小于第一种布局下的86″；无刷旋变B在第二种布局下的最大误差值69″小于第一种布局下的89″，即第二种布局下无刷旋变A和无刷旋变B的误差值均变小，说明两套无刷旋变的相互影响较小，同样表明第二种布局是更为合理的。

3.2.2 优选布局的电磁场计算

计算第二种布局下双裕度旋变的磁密云图如图11所示，磁密矢量图如图12所示。从图11、图12中可以看出，由于无刷旋变的激磁方为环变定子，环变齿较窄，环变中磁密较高。第二种布局方式将旋变布置在双裕度旋变的两端，旋变A受到环变B的影响减弱，旋变B受到环变A的影响也减弱，因此两套无刷旋变的角度偏差较小。

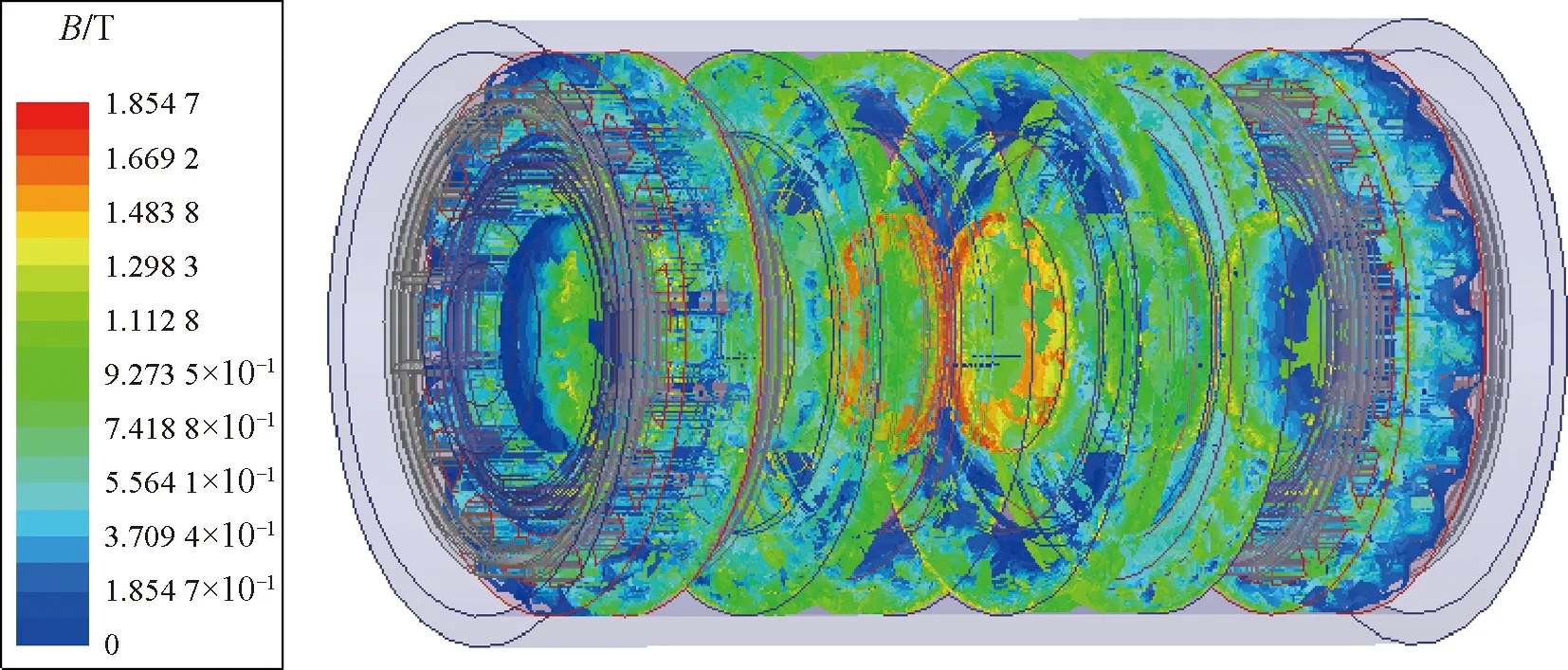
图11 磁密云图

图12 磁密矢量图

双裕度旋变转子转动一周，第二种布局方式下无刷旋变A和无刷旋变B的输出电压波形如图13所示。

图13 双裕度旋变输出电压

4 实验验证

按照以上分析及计算，确定双裕度旋变的设计方案并生产样机，主要设计参数如表7所示，样机实物图如图14所示。

表7 样机方案

图14 样机实物图

样机在各窜动位置下的输出电压和输出电压变化率如表8所示。测试结果均满足要求，证明本文的仿真分析方法是可行的。

表8 样机各窜动位置输出电压

样机转子在不同位置下两套无刷旋变同时工作时的输出角度偏差如表9所示。角度偏差最大为32″，满足实际使用要求。该角度偏差反映了无刷旋变A和B磁场的相互影响程度，实验测试结果与仿真计算结果为同一数量级，可以证明本文的仿真分析方法是可行的。

表9 样机各位置下输出角度偏差

5 结 语

在特殊应用场合，双裕度旋变在轴向窜动下使用，以及内部两套无刷旋变同时工作的使用需求。本文通过磁路法确定双裕度旋变的初步设计方案，再结合有限元仿真方法，确定双裕度旋变的优化方案，并以优化方案生产样机进行验证。本文的分析方法及设计思路，对类似产品的设计及优化具有参考价值。