欠驱动桥式起重机灰色改进模糊PID防摆自适应控制

师冬娜 郭 鹏 王晓敏

1北京市丰台区特种设备检测所 北京 100161 2华北电力大学控制与计算机工程学院 北京 102206

3北京科正平工程技术检测研究院有限公司 北京 100007

0 引言

桥式起重机在现代工业中不可或缺，往往需要专业人员现场操控，设备工作效率和人员安全极大地依赖于操作人员的默契和熟练程度，对人员要求很高。实际使用中，由于操作失误造成的起重机事故屡见不鲜。如何加强安全保障、提高工作效率，对起重机进行精准控制一直备受关注。然而，桥式起重机系统具有非线性、强耦合、欠驱动等特点，使用传统控制算法难以取得满意的控制效果。针对其复杂的动态特性，大量专家学者进行了广泛研究。文献[1-3]采用能量耗散理论对欠驱动系统进行控制器设计。文献[4-6]采用滑模算法对欠驱动系统进行研究。

模糊控制将模糊数学与控制理论相结合，采用不精确推理模拟人的推理过程[7]，能改进复杂系统的控制效果，在欠驱动桥式起重机相关研究中应用广泛。文献[8]采用分段线性化方法，利用模糊T-S模型对欠驱动系统进行控制，改进控制效果。分段线性化受摆角范围约束，在摆角较小时，可取得良好的控制效果，在摆角增大时，线性化模型与实际值差距增加，控制准确性降低。文献[9]采用模糊PID方法对欠驱动桥式起重机进行控制，取得一定的控制效果，但其以小车位移信息为模糊控制器输入，对摆角的抑制效果有限。

本文采用基于少数据、贫信息的灰色算法预测摆角变化趋势作为模糊控制器输入量，经过模糊运算、调整PID参数以改善控制效果。相对于以往对小车位移采用反馈控制，摆角采用完全开环控制，利用摆角与小车位移间的耦合关系进行防摆控制的常规模糊控制算法。本文摆角控制仍为开环控制，PID参数却可根据摆角变化趋势进行在线调整，在小车位移过程中对摆角抑制实现在线自适应控制，有效防止摆角增大。仿真结果表明，灰色预测摆角信息的改进模糊控制能够取得良好的防摆效果。

1 欠驱动桥式起重机模型

图1为欠驱动桥式起重机的示意图。小车质量为mc，在外力F的作用下沿导轨运行，位移为x。负载质量m、摆角θ，通过钢丝绳与小车连接，随小车运行而摆动，钢丝绳长度为L。二维桥式吊车系统有1个控制量F，2个自由量x和θ，其矩阵模型为[1]

图1 桥式起重机简化模型

在模型中，控制量直接作用于小车位移，使小车到达目标位置。在小车移动中，负载在惯性作用下摆动产生摆角。整理式(1)可得

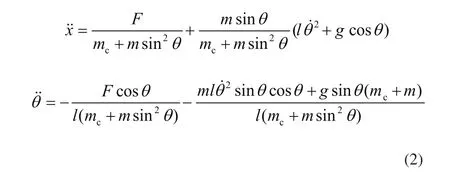
2 模糊PID控制

欠驱动桥式起重机模糊控制往往将位置误差信息作为模糊控制器的输入，暂称为常规模糊PID控制，其控制框图如图2所示。其中，G1为小车位移子系统，G2为负载摆角子系统，摆角子系统对位移子系统存在的单向强耦合效应，设为G21。

图2所示常规模糊PID控制，采用2输入3输出模糊控制器，以小车位置误差e=xd-x及误差变化率为输入量，以ΔKP、ΔKi、ΔKd为输出量，对PID控制器参数KP、Ki、Kd进行调整。PID控制器输出F控制x及θ，使x→xd(e→0)，θ→0。

图2 常规模糊PID控制框图

模糊控制器的输入量论域定义为：e论域：{-xd，xd}，论域：{-0.05xd，0.05xd}；输出量论域定义为：ΔKP论 域：{-KP，KP}，ΔKi论 域：{-Ki，Ki}，ΔKd论域：{-Kd，Kd}。其语言变量均定义为{NB，NM，NS，Z，PS，PM，PB}，采用三角形隶属函数，其模糊规则如表1～表3所示。反模糊化方法采用最大隶属度法将推理出的模糊集合转化为确定值作为模糊控制器的输出。

表1 ΔKP模糊规则

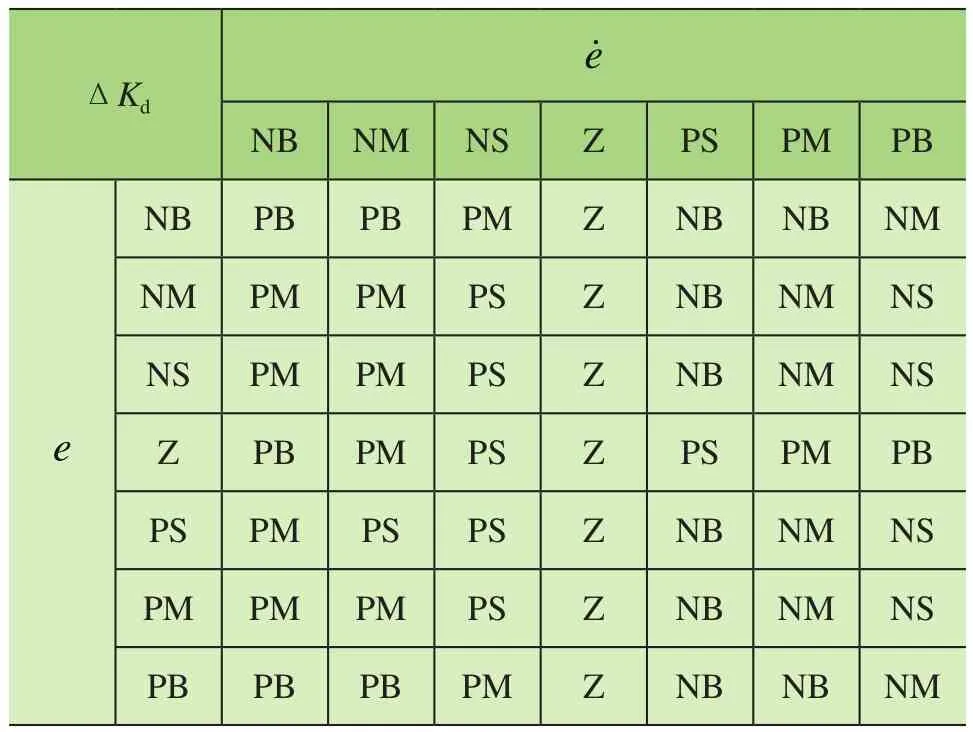
表3 ΔKd模糊规则

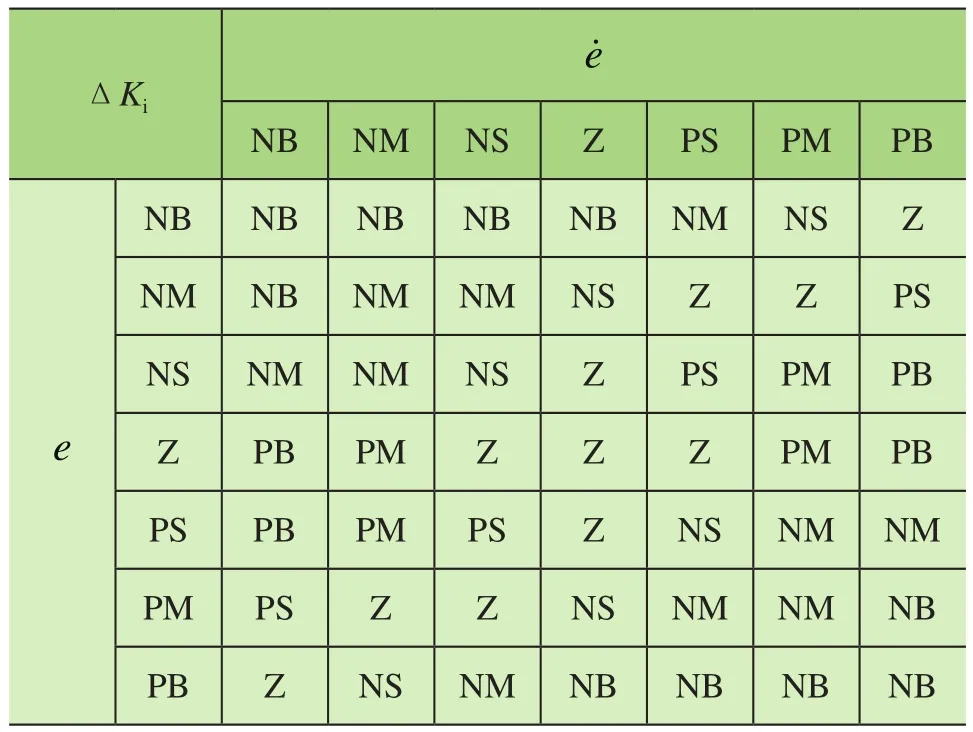
表2 ΔKi模糊规则

3 改进模糊灰色PID控制

欠驱动桥式起重机摆角子系统为开环子系统，无法进行反馈控制。图2采用常规模糊PID控制方法，单纯针对位置误差信息改进PID参数，利用摆角与小车位移间的耦合关系，防摆效果有限。为了进一步抑制摆角增大，使用旋转编码器校正角度传感器的方法，实时测量摆角角度传送给灰色预测模块，将摆角信息灰色预测量，反馈给模糊控制器，根据摆角变化情况制定模糊规则，在线调整PID控制器参数，其控制框图如图3所示。

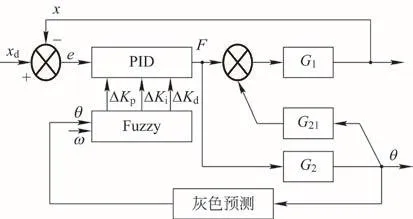
图3 改进模糊灰色PID控制

3.1 灰色预测模型

灰色预测控制将控制理论与灰色系统理论相结合，根据少量信息进行计算和推测。采用等维信息灰色GM(1，1)模型，即单变量一阶灰色预测模型，对摆角θ进行灰色预测。

k时刻灰色预测模型的输入摆角角度数据序列（简称角度序列）为

式中：n为灰色建模维数。

对该角度序列进行生成累加，得到一次生成累加角度序列为[10]

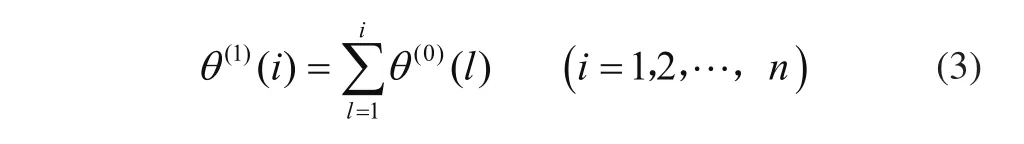
根据此序列，建立GM（1，1）灰微分方程为

式中：a为灰模型发展系数；b为灰作用量，用最小二乘法求出，其向量形式为

按式(7)以θ（0）（1）为基准进行n+1步的预测，并进行累减还原生成，得到第i步（i=1，2，…，n+1）的摆角角度预测值为

在每一新的采样时刻计算新的θ（0）（k+1），将其替代上一时刻的摆角角度值作为模糊控制器的输入量。

相对于直接采用当前一步的摆角及角速度进行模糊计算，灰色算法根据最近几步的摆角变化对下一步摆角θ进行预测，并根据预测结果作为其角速度ω=θ·的计算依据，两者共同实时反馈至模糊控制器作为其输入量，使模糊控制器根据摆角变化提前调整输出值，改进防摆效果。

3.2 改进模糊PID控制

图3对模糊控制进行改进，与常规模糊PID控制（图2）相比，仍然采用2输入3输出的模糊控制器，2个输入量为摆角θ及角速度ω，3个输出量ΔKP、ΔKi、ΔKd调整PID参数。改进后，摆角子系统仍为开环子系统，但摆角信息经过灰色预测反馈给模糊控制器，经过模糊运算实时调整PID参数，使PID控制器能根据摆角信息在线自适应调整，在控制小车到达指定位置时有效抑制摆角增大。

模糊控制器改进后，其语言变量、模糊化及反模糊化方法均与改进前常规模糊PID采用的方法相同。输入量论域为：θ论域：{-0.15，0.15}，ω论域：{-0.007 5，0.007 5}；输出量论域为：ΔKP论域：{-KP，KP}，ΔKi论域：{-Ki，Ki}，ΔKd论域：{-Kd，Kd}。

根据摆角变化通过模糊运算实现在线自整定PID参数。调整模糊规则见表4～表6。

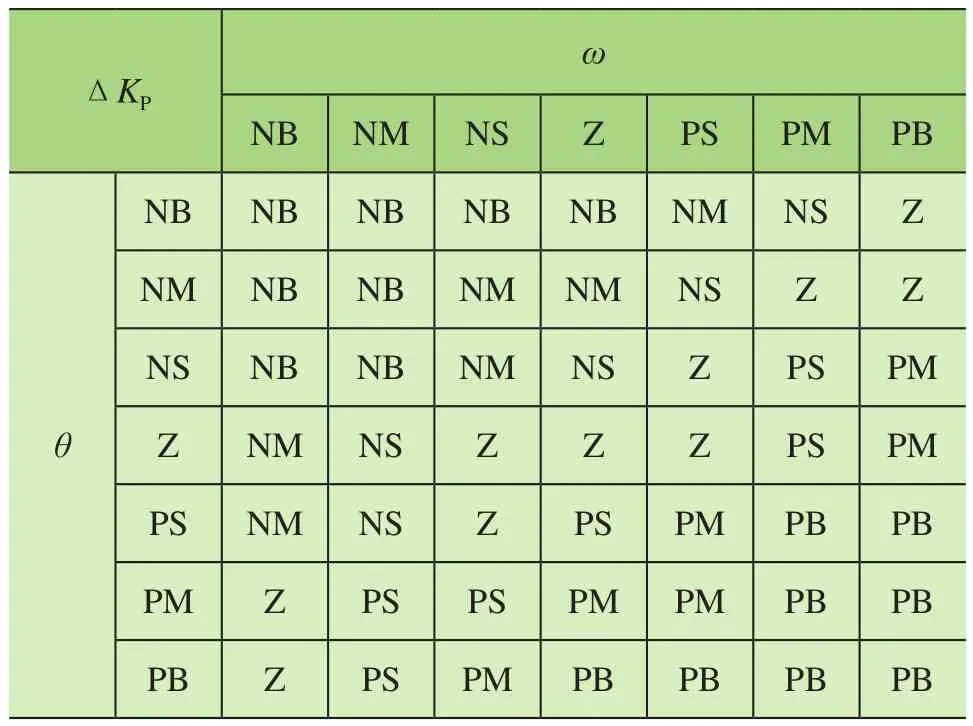
表4 ΔKP模糊规则

表6 ΔKd模糊规则

1）比例系数KP整定原则 KP可加快系统响应速度[10]。在小车运行至目标位置过程中，当摆角θ负向（N方向），角速度ω负向，说明摆角θ在负向增大，此时为防止|θ|过度增大，减小KP取值，即ΔKP取为负。当θ负向、ω正向，此时摆角θ由负向零点靠近，应适度降低KP取值，即ΔKP仍为负，适度降低调节力度。当θ为正（P方向）、ω为正，说明θ正向增大，此时增大KP，即ΔKP取正。当θ为正、ω为负，此时θ正向减少，适度调整KP增大力度，即ΔKP适度减少正向取值。在θ、ω均在零点附近时，为缩短调整时间，ΔKP取零（Z）。

2）积分系数Ki整定原则 Ki的作用是消除系统稳态误差[10]。在θ距离零点（Z）较远时，为防止产生积分饱和，引起较大超调，ΔKi取负（NB，NM，NS）；在θ距离零点较近时，当摆角与角速度同方向时，说明|θ|在增大，为减小超调，ΔKi取负；当摆角与角速度方向相反时，摆角向零线靠近，为了快速消除系统静态误差，ΔKi取正。当θ与ω均接近零点时，说明摆角子系统趋近稳态，此时ΔKi取Z。

3）微分系数Kd整定原则 Kd可在响应过程中抑制偏差向任何方向发展[10]。在实际调节中，ΔKd与ω密切相关，当ω为负、ΔKd取负，降低系统微分作用，避免系统提前制动。当ω为正、ΔKd取正，增强系统微分作用，对摆角变化加强干预。

表5 ΔKi模糊规则

4 仿真实验

采用Matlab仿真，采样时间Ts=0.01 s。设定小车初始位置x0=0 m，目标位置xd=4 m，钢丝绳长度L=2 m，小车质量mc=15 kg，负载质量m=5 kg，取重力加速度g=9.8 m/s2。

对欠驱动桥式起重机仿真曲线如图4所示，Curve1和Curve4是采用经典PID控制算法的小车位移及摆角角度仿真曲线，Curve2和Curve5采用常规模糊PID控制算法，Curve3和Curve6采用灰色改进模糊PID控制算法。

3种 控 制 方 法 的 PID参 数 为：KP=15，Kd=1，KP=30。灰色预测模型n=4。

由图4可以看出，对于小车位移，3种控制方法均可取得满意的控制效果，3种控制方法调整时间均在20 s上下，其中采用常规模糊PID控制算法的Curve2超调量略低，其他2种方法超调量接近。由此，3种控制方法均能有效控制小车位移，使其在超调量不高的情况下，快速到达指定位置。

由图4可知，在防摆方面，3种方法的控制效果差异明显。采用灰色改进模糊PID控制算法的Curve6明显优于其他2种方法，|θ|控制在0.13 rad以内，不足10 s即进入稳态。采用常规模糊PID控制算法的Curve5相对于采用经典PID算法的Curve4，可以取得一定的防摆效果，Curve5中|θ|控制在0.2 rad以内，而Curve4在0.3 rad左右。2种控制算法的调整时间接近，均在20 s左右。故对于摆角抑制常规模糊PID控制算法相比于经典PID算法可取得一定效果，但其模糊控制器以小车位移信息为输入量，防摆效果有限；灰色改进模糊PID算法将摆角信息进行灰色预测，作为模糊控制器的输入量改进PID控制效果，可取得良好的控制效果，防止摆角超调，迅速进入稳态。

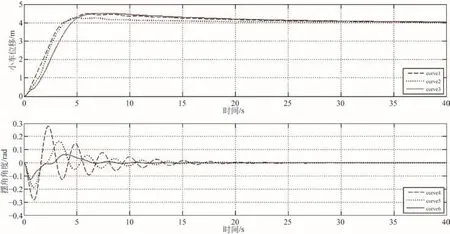
图4 3种控制方法仿真曲线

综上所述，3种控制算法均能有效控制小车位移。在小车位移控制效果相似的情况下，常规模糊PID算法采用位移反馈信息改进PID参数，对于摆角抑制具有一定的改进作用，但效果有限；灰色改进模糊算法在控制小车位移到达指定位置时，能够有效抑制摆角增大，明显改进摆角控制效果。

5 结论

二维欠驱动桥式起重机控制系统以小车位移为反馈信息，调整控制量F，控制小车位移x及摆角角度θ。本文为了改善负载摆角的控制效果，首先对摆角角度发展趋势进行灰色预测，将灰色模型输出的摆角信息作为模糊控制器的输入量，使PID参数根据摆角信息发展趋势进行在线调整，在小车位移时有效抑制摆角，实现防摆自适应控制。相对于经典PID控制和以小车位移为模糊控制器输入的常规模糊PID控制，此种方法，在小车位移控制效果相似的情况下，有效抑制摆角超调，缩短摆角控制调整时间。仿真试验表明，灰色改进模糊PID控制算法，可取得良好的防摆效果。