起重机大拉杆涡致振动模拟研究

潘欣钰 南海博 邢宇骏

中船第九设计研究院工程有限公司 上海 200090

0 引言

起重机的工作场地一般较空旷，当有环境风时将会在其大拉杆的两侧产生交替脱落的漩涡，从而使拉杆受到周期变化的侧向力。当风速达到一个合适的区间，其对于拉杆施加的周期力频率与固有频率较接近时，将会产生涡致振动。

很多学者已对方柱、圆柱等的涡致振动进行了研究,李广望等[1]数值求解计算了较小雷诺数下圆柱的涡致振动现象;胡影影等[2]研究了人工侧边界条件对数值模拟计算的阻塞影响；蒋定国等[3]采用物理分步法对方柱绕流的流动分离现象进行了大涡模拟；张伟等[4]采用粒子图像测速设备进行了方柱扰流实验。然而，针对大拉杆这类形体较复杂的工程实体如何避免强烈涡致振动的研究尚较少。因此，本文采用计算流体力学与结构有限元分析分别计算出大拉杆所受风力的变化频率与固有频率，并进行比较分析。在此基础上，通过增设扰流构件，通过上述模拟仿真方法对优化方案进行分析计算。

1 起重机大拉杆原型建模

根据实际工况，当起重机大拉杆发生风振时，其较低一端离地高度为40.8 m，较高一端离地高度为53.2 m。另外，测量风振时环境风速的仪器与起重机驾驶室为相同高度，离地26.7 m。风振时起重机大拉杆的姿态以及起重机驾驶室位置如图1所示。

图1 风振产生时起重机大拉杆姿态以及驾驶室位置

起重机大拉杆的长度为30.8 m，迎风高度为0.75 m，宽度为0.52 m，宽高比为0.7。在其上每隔4 m有一个长方形圆角孔洞，整根大拉杆共7个孔洞，大拉杆的几何特征如图2所示。

图2 起重机大拉杆几何特征

由于大拉杆不处于同一高度，最高点与最低点相差12.4 m，故在大拉杆的风振计算中必须考虑梯度风的影响。根据现场的情况，风速仪被安装于离地高度为26.7 m的驾驶室外。当产生风振时，风速仪显示的风速为13.0 m/s。风速和高度的关系可表示为

式中：Vh为离地h处的风速；V10为离地10 m处的基础高度风速；h为离地高度；α为梯度风指数，根据GB/T 3811—2008《起重机设计规范》[5]中表19风压高度变化系数Kh中的内容，α取值为0.3。

由驾驶室高度26.7 m处的风速为13 m/s带入式（1）可计算出10 m高度的基础风速V10为9.7 m/s，大拉杆所处的梯度风场可表示为

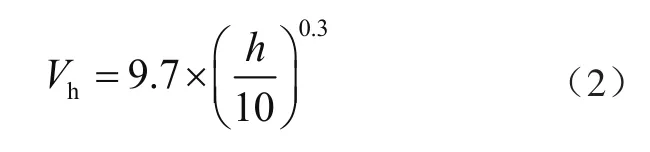
由上式计算得出的梯度风场离地高度与风速的关系如图3所示。当确定梯度风场后，通过三维建模软件对大拉杆进行建模，并将其导入到计算流体力学的网格划分软件当中，大拉杆的几何建模如图4所示。

图3 梯度风沿高度的风速分布

图4 大拉杆原型三维建模

根据产生风振时大拉杆的姿态，将其调整到合适的位置，考虑到风吹过大拉杆时将会产生湍流扩散，计算域应有足够的空间使空气波动不会影响到计算结果。本次模拟选取壅塞率（即大拉杆的迎风面积与风速入口面积之比）为0.25%，整个计算域风场宽度为88 m，长度为270 m，高度为100 m。计算流体力学场域尺寸与大拉杆原型的具体位置如图5所示。

图5 大拉杆计算流体力学模拟的计算域

2 计算流体力学数学模型

采用计算流体力学模拟软件，通过有限体积法数值求解计算域内的各类物理参数，本文涉及的计算参数有风速、压力等。涉及到2类控制方程，分别是连续性方程和动量方程。其中，质量守恒方程为

式中：ρ为流体密度，ui为x、y、z方向流体速度分量，xi指直角坐标系中的x、y、z方向，t为时间。

动量守恒方程为

式中：p为流体压力，μ为流体动力粘性系数，Si为外部源项。

3 大拉杆原型涡脱频率与固有频率模拟

在CFD软件中，将长方形计算域距离大拉杆较近的一端设置为速度入口，采用UDF将式（2）中速度剖面赋予该边界，相应的远端则设置为自由出流边界条件。大拉杆表面设置为无滑移壁面条件，湍流模型选择k-Epsilon的2个方程RNG模型，采用瞬态模拟，时间步长为0.01 s。另外，对大拉杆本体进行受力监控，考虑到大拉杆在现场产生风振时的振动为上下运动，可选择受力监控中的升力系数监控，并将其中的受力向量调整为X＝0、Y＝0、Z＝1，表示受力方向为Z方向，与实际振动的方向相同。经过迭代计算，结果收敛后大拉杆表面的压力分布情况如图6所示。

图6 大拉杆表面压力分布云图

大拉杆在振动方向上所受到的升力系数的时历曲线，如图7所示。由图7可知，在整个计算周期之内，大拉杆的升力系数呈现类似正弦波的变化，说明其受到一个周期性变化力的作用，若该力变化的频率和大拉杆自身固有频率较接近就会产生风振现象。软件升力系数监控的功能可将每个时间步中大拉杆所受升力系数记录为一系列时序数据，通过快速傅里叶变化（FFT）计算出其主要频率，具体情况如图8所示。

图7 大拉杆升力系数的时历曲线

由图8可知，升力系数的变化频率为 2.02 Hz，这是风在对大拉杆进行扰流后其湍流漩涡脱落的频率，只需将该频率与固有频率进行比较即可校核上述的模拟方法是否能够准确地计算大拉杆原型的风振频率，为后续的优化方案提供合适的计算评估方法。

通过有限元软件建立大拉杆的计算模型，选用实体单元，根据实际质量对大拉杆的密度进行适当调整，大拉杆按简支梁进行约束。经计算得到该大拉杆第1阶固有频率如图9所示。

图9 大拉杆1阶固有频率 （f＝2.29 Hz）

由图9可知，大拉杆的1阶固有频率f＝2.29 Hz，其振型沿大拉杆方向上下振动，振型方向与由风载荷引起的大拉杆涡致振动方向一致，该阶固有频率即为引起涡致振动的频率，也是涡脱频率需要尽量避免与其范围较接近的一个频率。

4 涡致振动判定

根据《风工程与结构抗风设计》[6]所阐述的锁定现象，即对于特定结构漩涡脱落频率fv与平均风速U成正比。然而，由实验观察可知，在结构产生涡激共振后，结构自振频率会控制旋涡脱落的频率，使其在一定风速范围内不再随风速变化而变化，直到风速增大较多后旋涡脱落频率才重新回到斯托罗哈数计算出的正常频率数值上，这一现象称为锁定（Lock-in）。

由上述可知，锁定现象与一定的风速范围相对应。对于细长型结构，由于其来流风速存在上大下小的规律，因此与锁定现象对应的风速往往位于结构某一高度区域内，该区域称为共振区。共振区定义为沿高度方向上取（1～1.3）Ucr的变化范围，Ucr为临界风速。由此可以推断，当涡脱频率介于100% h固有频率～130% h固有频率之间的范畴时将会产生涡致振动。另外，对于涡脱频率比固有频率小的情况，任安禄等[7]的相关研究发现当固有频率等于1.1倍的风振频率时，也会发生共振现象。

综上所述，涡脱频率介于90% h 固有频率～130%h 固有频率之间的范畴时将会产生涡致振动，而大拉杆原型的固有频率经计算为2.29 Hz。如果旋涡脱落频率如果在90% h 固有频率～130% h 固有频率之间，即2.06～2.98 Hz，则会产生风振现象。计算流体力学软件计算出的旋涡脱落频率为2.02 Hz，与会产生风振现象的频率下限的误差为1.9%，考虑到计算流体力学软件以及有限元软件本身模拟精度所带来的误差，以及现场梯度风的脉动特性，在实际情况中采用2类软件计算出的涡脱频率和固有频率如此接近时，很有可能二者已处于会发生涡致振动的范围内，造成相关设备构件的安全性问题。

5 大拉杆优化方案及模拟结果

为了减小大拉杆的涡致风振损害，对其进行形体优化。在大拉杆的7个孔洞位置中增加导流板，为了使气流掠过大拉杆后的扰流变得更趋向于随机过程，在相邻孔洞内设置相反方向的导流板，当风吹过导流板时将会产生大小不同的旋涡，破坏原本在大拉杆上部和下部的旋涡周期性脱落节奏，这样就能避免大拉杆在Z轴方向上受到一个周期性变化的力，从而降低其在一定的风速下产生大幅度共振的可能性。具体的导流板设置方式如图10所示。

图10 导流板设置方式示意图

该工况同样采用前述的模拟计算方法来评估其风振的可能性。针对优化方案重新构建几何模型，并划分网格，在设置导板的区域可适当增加网格密度，计算场域不发生变化，大拉杆优化方案三维模型如图11所示。

图 11 导流板优化工况三维模型

该工况模拟与原型模拟基本相同，同样是利用CFD模拟的监控功能获得的导流板工况下升力系数的时历曲线如图12所示。

图12 增加导流板大拉杆的升力系数时历曲线

由图12可知，在模拟的时间段内，大拉杆所受到的力并未呈现周期性变化，而是慢慢收敛到一个稳定的数值，说明此时湍流产生的旋涡对称脱落的结构已被破坏。从大体量旋涡角度看，相当于任何时刻其从上部和下部脱落的旋涡数量、尺寸较平衡，使大拉杆在Z轴方向的升力系数也在一段时间后逐渐收敛于一个稳定数值。

6 结论

1）针对形体较复杂的构件（如本文研究对象起重机的大拉杆），相关标准、规范上并无其斯托罗哈数的取值，这就意味着无法计算其风振频率。因此，本文采用了计算流体力学软件模拟旋涡脱落频率，有限元软件模拟固有频率的解耦仿真计算方法来研判对象是否会在特定风速下产生涡致振动的可能性，并采用现场发生风振时的实际风速进行模拟，从而验证了该套方法的可行性。

2）大拉杆原本的几何形体在现场反应有风振时所测定的风速（26.7 m高处风速13 m/s）情况下，分别利用计算流体力学软件和有限元软件进行了旋涡脱落频率和固有频率的模拟，发现旋涡脱落频率距离会产生共振的频率下限只相差1.9%，考虑到2类模拟软件的计算精度和现场自然风的脉动性，可认为将会产生涡致振动的状况，从而验证了上述模拟方法能评判复杂形体在特定风速下的风振可能性。

3）根据相关研究文献，当研究对象的旋涡脱落频率（即为物体振动方向上所受周期力的频率）介于固有频率的0.9～1.3倍范畴时，将有较大可能产生涡致振动。

4）在类似大拉杆的长方体构件上开洞将会使其斯托罗哈数变小，但并不能保证其不会发生涡致共振。因为开洞依然较为有规律，无法影响大拉杆上下部分扰流形成的旋涡对称性周期脱落。但是，斯托罗哈数变小可使该构件在较高风速下才会产生共振，设计时可依据现场所能达到的风速予以校核。

5）本文在大拉杆原型基础上提出增加孔洞导流板的几何优化方法（即在洞口增设方向不同的导流板），经过计算流体力学软件模拟可知，其受力在一段计算时间后趋向于一个稳定的数值，也就是说这类结构能够破坏构件所受风力的周期性。因此，判定这该优化方案在给定的现场风速下不会产生持续的涡致振动，在其他风速下也不会产生相应的较大共振。