基于时域叠加的声学埋地PE管道定位新方法

葛 亮 王 甜 肖小汀 吴佳晔 Mark Robinson 卓 勇 杨国强

1. 西南石油大学机电工程学院 2. 西南石油大学电气信息学院

3. 纽卡斯尔大学工程学院 4. 中国石油西南油气田公司燃气分公司

0 引言

地下管道定位技术在地下管道普查、建设城市智慧管廊的开展下逐渐成为各领域学者的研究热点[1-2]。随着工业的发展，聚乙烯（Polyethylene，PE）管道由于安装维护方便、价格低、耐腐蚀和使用年限长等优点，在城镇中、低压燃气管网建设中被广泛应用[3-5]。但由于管道信息系统不完善，且已有的埋地PE管定位技术不成熟，导致PE管道位置不明确，在施工建设中极易被破坏[6]，从而引发天然气泄漏、爆炸甚至人员伤亡事故。因此，实现埋地PE管的准确定位对保障城市建设安全具有十分重要的意义。然而PE管不导电、不导磁，定位难度大。目前已有的埋地PE管定位技术有电磁—示踪线法、探地雷达法、声学定位法和电子记标法[7-11]。其中，声学管道定位法[12]具有可在多种路况下使用、不受管道材质的限制、不需要与管道接触等优势，已成为当前研究的热点[13]。

声学管道定位技术有两种方式[14]：①将声波注入管道[15-16]，通过检测从管道内传播到地面的声波来定位管道，但需有可用于注入声波的管道连接口，且探测距离有限，只能确定管道的水平位置及走向[17]；②使用振动源击打地面产生弹性波，弹性波在土壤—PE管交界面会被管道表面反射回地面，通过地面传感器阵列检测的反射回波信号定位管道，因此也称为弹性波反射法。根据振动源激励信号以及回波信号处理方式的不同，弹性波反射法可分为互相关函数法和时域叠加法[12]。互相关函数法采用线性调频信号作为激励信号，但其操作复杂，且对激励信号要求较高。Papandreou等[18]通过计算检波器阵列检测信号与激励信号之间的广义互相关函数并求和以生成地面的横截面图像，定位出了埋地混凝土管道。Muggleton等[19]指出由于横波波长小于纵波波长，因此可以使用横波分量来提高定位分辨率，同时提出使用振动源附近的参考检波器信号代替激励信号求互相关函数，可以减轻附近其他潜在振动源的影响，提高检测信噪比。崔希望等[20]通过仿真分析了不同类型声源对埋地管道探测结果的影响，结果表明增加声源信号的频率成分可有效提高探测精度。而时域叠加法使用简单的短时脉冲信号作为激励信号，计算方便。Sugimoto等[21-22]通过研究浅埋物体的探测问题，提出了基于反射波叠加的地下成像方法，即时域叠加法。该方法假设待测目标发生点反射，并利用回波信号到达传感器距离不同而引起的时延不同来定位目标。Chen等[23]通过仿真研究了管道埋深、管道尺寸以及混合土壤对检波器信号的影响，验证了利用时延信息定位埋地PE管的可行性。在使用弹性波反射法定位埋地PE管的研究上，最成功的商业化产品是美国杰恩公司的声学管线定位仪（Acoustic Pipeline Locator，APL）[24]，国内许多燃气公司也逐渐引进APL作为探测埋地燃气PE管的主要设备。

相比国外拥有声学管线定位产品而言，国内在此方面的研究较晚，目前还依赖于国外已有产品定位埋地PE管[25]。随着国外对中国技术封锁越来越严密，开发国内自主研发的埋地PE管定位技术十分迫切。目前，互相关函数法相对成熟，已经实现了埋地塑料管和金属管的定位，而时域叠加法还未应用于现场埋地PE管定位测试。为了进一步验证时域叠加法定位埋地PE管的可行性，笔者对基于时域叠加的声学PE管定位方法进行了研究。首先研究了弹性波在土壤中的传播特性，建立了弹性波在土壤—PE管交界面处的波形转换模型，其次提出了基于时域叠加的埋地PE管定位方法，然后使用COMSOL有限元分析软件进行仿真分析，验证了定位方法的准确性，最后进行了现场埋地PE管定位测试并得出相应结论。

1 弹性波在土壤—PE管介质中的传播理论模型

1.1 线性弹性体中的弹性波传播理论

研究弹性波在土壤和PE管介质中的传播时，将土壤和PE管假设为各向同性线弹性材料会有误差。笔者主要研究利用弹性波反射性质定位埋地PE管，为了简化研究，研究假设土壤和PE管为各向同性线弹性材料。

弹性波在线性弹性体中的运动方程为Navier方程：

对位移向量u应用Helmholtz定理，将其表示成一标量势φ的梯度和一向量势ψ的旋度之和[26]，得下式：

对式（1）两边取散度可得无旋波的波动方程：

式中θ表示体积膨胀系数；c1表示无旋波的传播速度，m/s。

对式（1）两边取旋度可得等体积波的波动方程：

式中ω表示转动向量；c2表示等体积波的传播速度，m/s。

通常无旋波也叫纵波，波阵面上质点的位移方向与波的传播方向相同。等体积波也叫横波，波阵面上质点的位移方向与波的传播方向垂直。

1.2 弹性波在土壤—PE管分界面的反射和透射

弹性波在异种媒介的边界面会引起反射、透射以及波型转换[27-28]，这正是各种检测所需的。考虑二维平面中弹性波在土壤—PE管分界面的反射和透射，以PE管中心为坐标原点建立直角坐标系Oxy如图1所示。

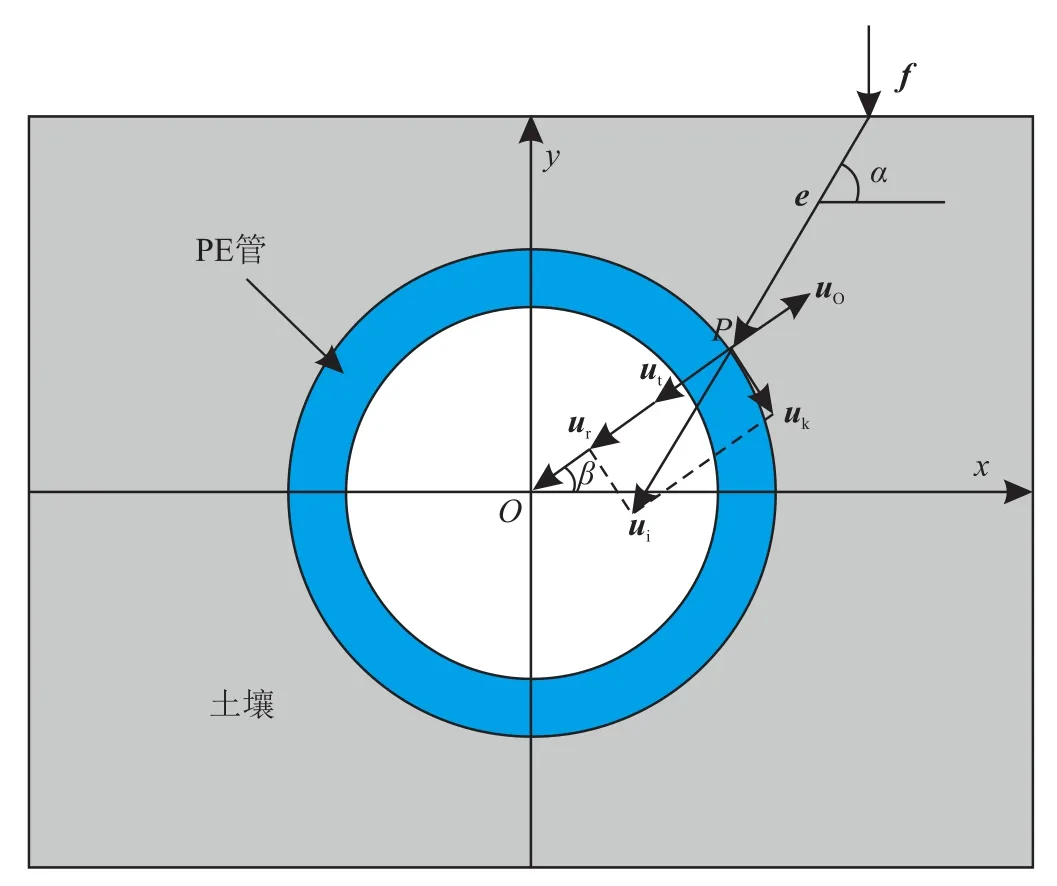
图1 纵波在土壤—PE管分界面的反射和透射图

图1中f为施加的激励，在f作用点处向土壤中辐射球面弹性波。对于球面波的其中一个波矢e，其与x轴夹角为α，此方向上的弹性波入射到PE管道上的P点，管道中心O与P点的连线与x轴夹角为β。对于入射纵波，其波阵面上质点的位移方向与波传播方向相同，于是在P点入射纵波的位移向量ui与波矢e的方向相同。将位移向量ui分解为沿管道径向和切向两部分，分别为ur和uk，则位移向量的关系为：

式（5）中ur又可分为透射入PE管道内的位移向量ut和被PE管道表面反射回土壤中的位移向量uo。球面入射弹性波被圆柱形PE管道表面反射后的回波仍然为球面波，所以此时uk为入射纵波引起的反射回波中的横波位移向量。与ut方向相反的uo为入射纵波引起的反射回波中的纵波位移向量。

对于入射横波，其波阵面上质点的位移方向与波传播方向垂直。对于与x轴夹角为α的波矢e，此方向上的入射横波在PE管道上Q点处位移向量为wi，其与波矢e垂直，如图2所示。

图2 横波在土壤—PE管分界面的反射和透射图

将位移向量wi分解为沿管道径向和切向两部分，分别为wr和wk，则位移向量的关系为式（6）：

同理，wr也可分为透射入PE管道内的位移向量wt和被PE管道表面反射回土壤的位移向量wo。类似于对入射纵波的讨论，wo为入射横波引起的反射回波中的纵波位移向量，wk为入射横波引起的反射回波中的横波位移向量。

2 基于时域叠加的埋地PE管定位方法

利用弹性波遇到异种媒介发生反射的性质进行埋地PE管定位的原理是首先根据已有的施工信息大致判断PE管的走向，然后在地面布置多条等间距的与管线大致方向垂直的测量线（图3）。每条测量线上布置一个振动源和多个等间距的地震检波器。图3中每条测量线上有6个检波器，实际探测时可根据现场条件确定检波器数量及其间距。

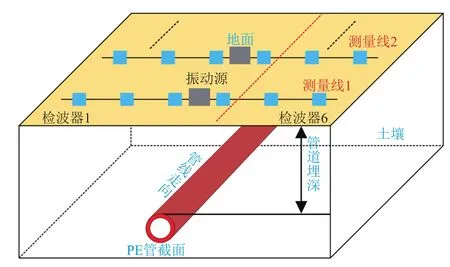
图3 用于管线定位的测量线布置示意图

对于每条测量线，工作时给振动源施加一激励信号激发出弹性波，弹性波在土壤中传播并到达PE管表面，然后被PE管表面反射，再次在土壤中传播到达地面，最后被地面检波器拾取。由于弹性波从振动源到达土壤—PE管交界面再被反射回各检波器的传播距离不同，导致各检波器的输出信号在时间上将具有不同的延迟，该时间延迟信息就包含了PE管相对于各检波器的位置信息。从每条测量线上的检波器输出信号中获取管道位置信息，然后连接所有测量线上的管道位置标志点，就可确定管道走向。

取图3中的任意一条测量线，沿该测量线做一垂直于地面的测量面，以测量线为x轴建立坐标系，如图4所示。检波器间距为d，振动源位于检波器阵列中心。假设管道埋深为H（实际为PE管道中心到地面的距离，这里简化为PE管道顶点到地面的距离），到y轴距离为xo。弹性波从振动源到达埋地PE管表面，再被PE管表面反射回第i个检波器的传播距离为：

图4 一条测量线上的传感器布置图

式中si表示传播距离，m，i取1～6。假设弹性波传播速度已知，则弹性波由振动源到PE管，再被PE管表面反射回第i个检波器的传播时间为：

式中ti表示传播时间，s；c表示弹性波波速，m/s。

令yi为第i个检波器输出信号，τ为激励信号持续时间。假设振动源激励信号起始时刻为0，则yi出现的时刻为ti。此时，若将各检波器的输出信号yi在时域平移ti，则各检波器的输出信号在时间轴上将重合，只是幅值有差异。

基于上述思想，运用各检波器输出信号获取PE管道位置信息时，首先将图4中的测量面按一定步长在x轴正方向和y轴负方向进行离散化，将测量面划分为N个正方形小单元。然后对第k个单元，取其几何中心并将其作为反射点。假设第k个单元的几何中心坐标为（xk，yk），将式（7）中的xo、H分别用xk、yk替换，便可通过式（7）、（8）计算出弹性波从振动源到反射点再到第i个检波器的传播时间tik，然后将第i个检波器的输出信号yi在时域平移tik，平移后的信号为yik。若第k个单元所在位置不是PE管道位置，则各检波器输出信号在时间轴上将不重合。相反，若第k个单元所在位置是PE管道位置，则各检波器输出信号在时间轴上将重合。最后，将移位后的各信号相加并在0～τ内积分[29]，令积分值为Mk，可得：

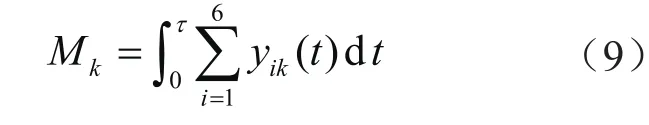
对于离散采样信号，式（9）中的积分变为0～τ内的有限个离散值叠加，因此该定位方法被称为时域叠加法。对N个单元进行同样操作，得到N个叠加值。在N个叠加值中，显然只有PE管所在单元的叠加值最大。因此，与最大叠加值对应的单元即为PE管所在位置。

3 埋地PE管定位仿真与结果分析

3.1 模型建立

使用COMSOL有限元分析软件进行埋地PE管定位仿真分析，验证第2节理论模型和第3节定位方法的正确性。土壤假设为砂土，PE管材料为MDPE，主要参数如表1所示。

表1 材料参数表

二维仿真模型如图5所示。通常埋地燃气PE管的埋深介于0.5～2.0 m，模型中PE管埋深为1.4 m，设置6个检波器，检波器间距为0.5 m。由于检波器与土壤接触点很小，因此在仿真中将检波器简化为点。同时，振动源用一个速度激励源代替，使用高斯脉冲调制的正弦信号作为激励速度信号。

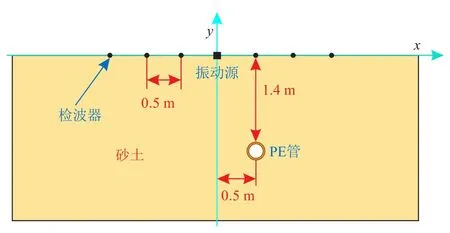
图5 仿真模型图

3.2 仿真结果分析

3.2.1 弹性波在土壤—PE管介质中的传播情况

为了直观地观察弹性波在土壤中的传播和在PE管表面的反射情况，绘制了不同时刻土壤域的表面速度（y分量）分布云图如图6所示。

图6-a为0.007 0 s时的速度云图，可知弹性波传播一段时间后，其波阵面逐渐分为两部分：①一部分波阵面靠前，为波速较大的纵波（P波）；②一部分波阵面靠后，为波速较小的横波（S波）。图6-b为0.010 0 s时的速度云图，此时P波已被PE管道表面反射，S波尚未到达PE管道。考虑到弹性波在土壤—PE管道交界面会发生波型转换，因此被反射的P波将分成两部分，分别为入射P波在PE管道表面引起的反射P波和反射S波，图6-b中分别用RPP波和RPS波表示。图6-c为0.015 2 s时的速度云图，此时S波也被PE管道表面反射，产生RsP波和RsS波。

图6 不同时刻土壤域表面速度分布云图

3.2.2 时域叠加成像

6路检波器接收速度信号如图7所示，现通过时域叠加法对埋地PE管进行定位。

图7 检波器1～6接收速度信号图

首先对定位区域进行离散单元划分，为方便计算单元中心坐标，如图5所示建立坐标系。根据检波器阵列长度，确定划分区域为3.2 m×2.2 m的矩形，由于模型中PE管直径为0.2 m，为减少定位时间，选取边长0.2 m的正方形单元对定位区域进行离散，则离散单元数目N为176。接着根据每个单元的几何中心点计算176个单元对应的延时叠加值，构成一个11×16的矩阵M。记矩阵M中第i行第j列的元素值为Mij（i=1～11，j=1～16），其中最大值对应的i=8，j=11。由定位区域离散过程可知，最大叠加值对应单元的几何中心坐标为（0.5 m，－1.5 m），此时由时域叠加法得到的单元几何中心点表示的是埋地PE管道的顶点。而实际PE管道顶点坐标为（0.5 m，－1.4 m），定位误差为0.1 m（定位误差为实际管道顶点与定位出的管道顶点之间的距离），验证了使用时域叠加法定位埋地PE管的可行性。将矩阵M按照矩阵元素值的大小转换为彩色图，即可对定位区域成像，结果如图8所示，黑色圆圈代表PE管道实际位置，其所在单元的颜色最亮，因此可通过找到成像图中颜色最亮的单元的几何中心来定位埋地PE管。

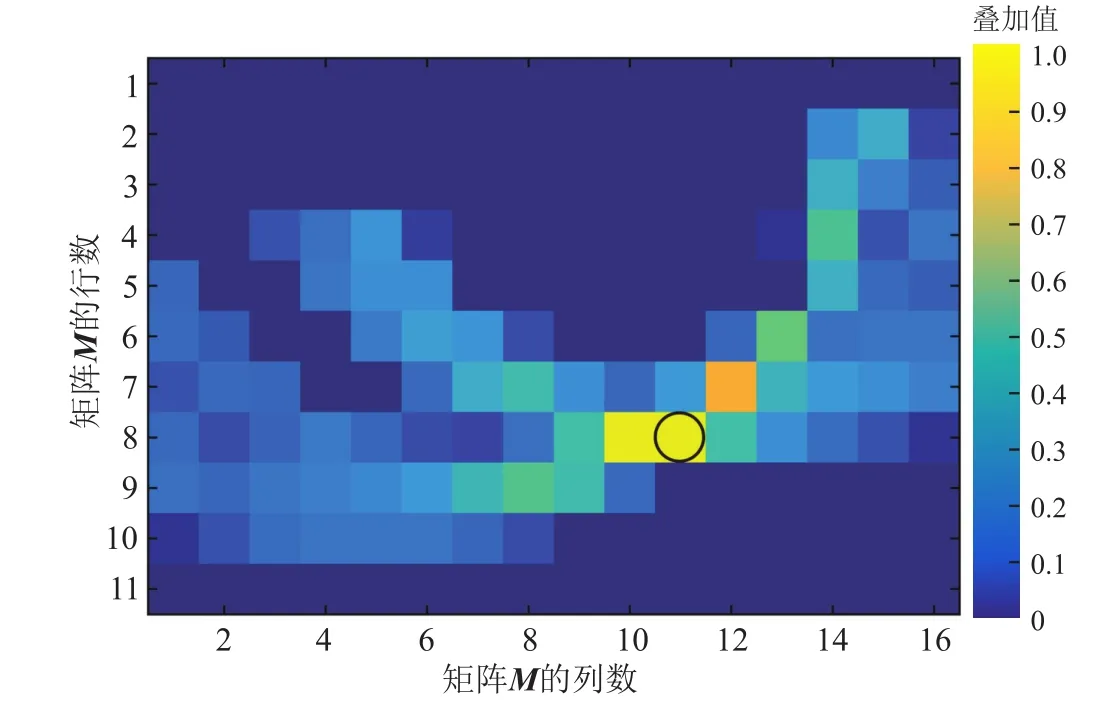
图8 定位区域成像图

4 现场测试与分析

为验证基于时域叠加的埋地PE管定位方法的实际定位效果，分别进行了管道埋深为0.5 m、1.0 m、1.5 m的现场PE管定位测试。测试设备包括DH40200型激振器、与激振器配套的DH5872型功率放大器、产生脉冲激励信号的RIGOL DG4062型函数信号发生器、检波器阵列、上位机以及USB5631数据采集卡等。现场测试时，信号发生器产生的激励信号通过功率放大器放大后，驱动激振器产生弹性波信号。

4.1 土壤波速测试

使用时域叠加定位方法对地下管线进行定位时，需先确定土壤波速，由于纵波波速大于横波波速，意味着检波器最先接收到的反射回波是纵波反射波，因此计算纵波波速，第一次实验现场波速测试方法如图9所示。使用激振器激发出弹性波信号，通过排列在一条测线上的间距为0.1 m的检波器阵列接收信号来确定表面波速度，然后根据表面波波速与纵波波速之间的关系得到纵波波速。

图9 波速测试仪器布置图

将检波器与激振器之间的距离和接收信号起始时刻做最小二乘拟合，由拟合后的一次函数的斜率可得到表面波波速，最小二乘拟合结果如图10所示，其斜率为75.00 m/s，因此表面波波速为75.00 m/s。

图10 表面波波速最小二乘拟合图

土壤的纵波波速与表面波波速之间的关系只与土壤的泊松比有关，测试场地土壤的泊松比大约为0.4，可得到土壤的纵波波速大约为192.70 m/s。第二次与第三次实验现场波速测试方法与第一次相同，得到纵波波速分别为201.50 m/s和211.21 m/s。

4.2 埋地PE管定位测试

4.2.1 0.5 m埋深PE管定位测试

首先根据现场环境大致确定管道走向，然后沿垂直于管道走向的方向布置若干条测量线（图11），现场管道走向及测量线布置示意图如图11-a所示，共布置5条测量线。以图11-a中第1条测量线为例，该条测量线上仪器布置如图11-b所示。检波器间距为0.3 m，其中参考检波器尽可能紧挨着激振器，其输出信号用于确定其他检波器接收信号起始时间。PE管大致位于各测量线上检波器3的正下方。

图11 0.5 m埋深测量线布置图

测量线1上的6路检波器接收信号如图12所示。根据埋地PE管定位方法对检波器信号进行处理，得到测量面1成像图如图13所示。图13中，颜色最亮的单元几何中心坐标为（0.215 m，－0.475 m），而实际埋地PE管顶点坐标为（0.300 m，－0.500 m），定位误差为0.090 m。

图12 6路检波器信号图

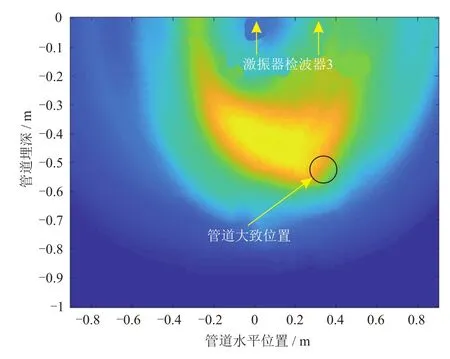
图13 测量面1成像图

对其余4条测量线的检波器信号进行处理，得到测量面2～5的成像图如图14所示。图14-a、b、c、d中颜色最亮的单元几何中心坐标依次为（0.295 m，－0.425 m）、（0.3 m，－0.45 m）、（0.28 m，－0.415 m）、（0.305 m，－0.435 m），则定位误差依次为0.075 m，0.050 m，0.090 m，0.065 m。

图14 0.5 m埋深PE管定位测试成像图

4.2.2 1.0 m埋深PE管定位测试

1.0m埋深PE管定位测试现场测量线布置及测量线1仪器布置如图15所示。根据现场环境共布置4条测量线，检波器间距为0.15 m，各测量线上PE管大致位于激振器正下方。测量面1～4的成像图如图16所示。定位误差依次为0.226 m、0.212 m、0.195 m、0.243 m。

图15 1.0 m埋深测量线布置图

图16 1.0 m埋深PE管定位测试成像图

4.2.3 1.5 m埋深PE管定位测试

1.5 m埋深PE管定位测试现场测量线布置及测量线1仪器布置如图17所示。由于现场环境较复杂，检波器放置比较困难，只布置2条测量线，检波器间距为0.15 m，PE管大致位于激振器与检波器2之间。测量面1～2的成像图如图18所示。定位误差依次为0.299 m、0.304 m。

图17 1.5 m埋深测量线布置图

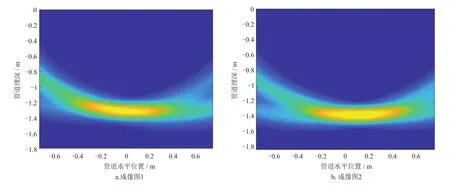
图18 1.5 m埋深PE管定位测试成像图

5 结论

1）通过分析弹性波在土壤中的传播特性可知，土壤中传播的声波可分为纵波和横波，其在土壤—PE管道分界面将发生反射、透射以及波形转换。其中反射回地面的弹性波包含了地下管道位置信息，因此可利用反射回波信号来定位埋地PE管。

2）基于COMSOL进行了埋地PE管定位仿真分析，仿真结果表明到达土壤—PE管道交界面的弹性波会发生波型转换，证明了理论模型的正确性。使用时域叠加法对仿真得到的6路检波器信号进行处理并对定位区域成像，由成像图可较准确地定位出埋地PE管，图中颜色最亮的单元几何中心点表示的是埋地PE管的顶点。

3）分别进行了埋深为0.5 m、1.0 m、1.5 m的PE管定位测试，最大定位误差依次为0.090 m、0.243 m，0.304 m，即管道埋深越大，定位误差越大。其主要原因是反射回地面的弹性波信号随传播距离越大，衰减越大，使得定位结果更易受周围潜在干扰的影响。本文进行的管道定位测试在土壤密实且均匀的环境下取得了较好的测量效果，但是对于土质分布不均匀且杂质较多的土壤环境仍然有很大的研究空间。本文研究的定位方法可以满足现场定位埋地PE管的需要。