考虑时空特性及时间成本的电动汽车有序充放电策略

王 鹤，冷贤达，潘禹含，边 竞，余中枢

（1. 东北电力大学 现代电力系统仿真控制与绿色电能新技术教育部重点实验室，吉林 吉林 132012；2. 国网吉林省电力有限公司吉林供电公司，吉林 吉林 130000；3. 国网江西省电力有限公司南昌供电分公司，江西 南昌 330000）

0 引言

电动汽车（EV）是一种高效、清洁的出行方式，且具备良好的灵活性和储能特性，在合理的调度策略下可缓解电网中负荷的压力，实现削峰填谷。但EV 出行的随机性导致其充放电功率特性复杂，现已可采用多种方法对EV的时空负荷进行建模。例如：文献［1］采用考虑出行链的方式模拟EV 充电特性，建立了EV充电需求模型，为后续制定调度策略的工作奠定了基础；文献［2］将地理信息系统（GIS）数据与出行链相结合，使EV 出行模型更加精确，但其出行链相对固定，无法体现EV 真实的行驶情况；文献［3］根据出行链和马尔可夫决策理论，建立了计及出行路径随机性的EV时空接入模型，解决了传统出行链过于固定的问题，但其考虑的车型较为单一；文献［4］考虑了实时的动态车流，提出了更加符合实际情况的EV 充电负荷时空分布概率模型；文献［5］提出了一种基于改进重力模型的EV 负荷时空分布建模方法，提升了模型的准确性。

为充分利用大量EV这一优质储能资源，许多学者采用动态电价引导EV的充电行为。文献［6］提出了一种计及多车交互影响的EV 与快充站动态响应策略，提高了EV 充电寻站的效率。文献［7］提出了一种以电网侧与用户侧双方合作收益最大为目标的EV 充放电优化调度模型，达到了双边共赢的目的，但并未考虑充电站的收益。文献［8］提出了一种基于动态电价的分层调度策略，充分挖掘了车主参与调度的潜力及意愿，但只考虑了2 种车型，难以对大量EV 进行精准调度。文献［9］提出了考虑EV 响应程度的分时电价策略，提高了车主的满意度及参与度，但车主参与度过高时，会使得谷时再次形成充电高峰，危害电网安全运行。

为解决上述问题，需要建立考虑多种车型EV时空特性与参与调度满意程度的优化调度策略，进一步引导车主有序地进行充放电。为此，本文首先分析了4 种不同车型的时空特性，建立了EV 时空负荷模型。然后，考虑了用户出行的便利性与参与调度的满意度，引入时间成本与参与调度的概率模型，提出了一种考虑车主时间成本与EV 时空特性的有序充放电策略。最后，通过仿真验证分析了本文所提策略的有效性，结果表明该策略在降低用户的成本、提升充电站收益的同时，实现了削峰填谷，提高了电网运行的安全性。

1 EV时空特性及充电模式模型

1.1 EV时间特性模型

EV 集群出行时间特性符合正态分布，假设每辆EV 每天最多参与一次调度，但其是否进行充放电则要根据其初始电池容量EEV进行判断。EV接入电网的时间fs(x)与EV 离开电网的时间fe(x)服从正态分布［10］，具体表达式分别见附录A 式（A1）、（A2），其参数见附录A表A1。

本文在有序充放电策略模型中考虑了车主出行的时间成本，其物理意义为离开时间变化对车主出行造成的不便影响。该成本主要受到车主时间敏感系数的影响，量化了EV 车主调整出行链的不方便性。不同的EV车型对应不同的时间敏感系数，由于出租车的休息时间十分有限，其时间敏感性均为0.4；公交车的充电时间会受到排班的影响，通常在夜间和休息时间进行集中充电，故公交车的时间敏感性均为0；私家车和公用车的时间敏感性会受实际情况影响，随机性较强。4 种车型EV 的时间敏感系数分布见附录A表A2［11］。

1.2 EV空间特性模型

交通路网可以抽象成由线段和点所构成的网络图，本文采用图论方法对交通路网进行建模。道路交叉节点用整数序列｛1，2，…，m｝（m为节点数）表示，从节点i向节点j方向行驶的道路用有向边（i，j）表示。不同车型的EV对应不同的出行目的，本文将城市分为4 种区域，分别为住宅区、工作区、商业区及综合区。由于出租车的出行链更多地受乘客出行目的的影响，出行目的分布较为随机；公交车的行驶路线固定，故并未对公交车的出行目的进行划分；私家车在工作日更多的是在住宅区与工作区之间往返；公用车则受其工作需要影响，更多的是在工作区、商业区及综合区内行驶。每种车型对应的出行目的见附录A表A3［12］。

已知道路首末节点的经纬度坐标，可由式（1）计算2 个节点间的直线距离，考虑实际道路有一定的曲折和坡度，仿真时乘以曲折系数1.15。

道路状况与天气温度是决定单位里程行驶能耗的2 个关键因素，EV 在不同路况的道路上行驶时对应不同的单位距离能耗量，而温度d的变化除了会对电池的损耗造成影响之外，还会影响EV的空调开启率Don。

本文将城市道路分为4 种等级，分别为快速路、主干路、次干路和支路，每种等级的道路在不同的交通路况下具有不同的车速v，单位里程行驶能耗的计算公式如下：

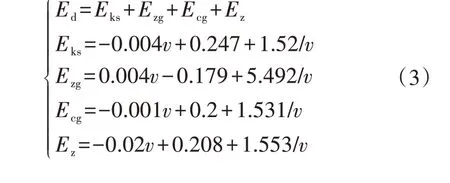
式中：Ed为单位里程行驶能耗；Eks、Ezg、Ecg、Ez分别为在快速路、主干路、次干路、支路上的单位里程行驶能耗。

不同温度下的空调开启率Don可以表示为：

1.3 EV车主参与调度的概率模型

若充电成本越低、调度距离越近，则EV 车主的响应意愿越大。本文设置了响应意愿指标D作为EV 车主对调度距离及调度价格满意程度的综合指标，其计算公式如下：

式中：C为车主充电成本；L为调度距离；α1、α2为权重系数，对于不同类型的EV选取不同的数值。

根据文献［13］建立EV 车主参与调度的概率模型如图1 所示。图中曲线包含车主参与调度概率PEV与响应意愿指标D之间关系的乐观曲线fmax与悲观曲线fmin，其计算方法分别见附录A式（A3）、（A4）。乐观曲线fmax表示EV 车主参与调度的概率上限，而悲观曲线fmin表示EV 车主参与调度的概率下限，则EV 车主参与调度的概率将会从乐观曲线与悲观曲线之间的范围随机选取。

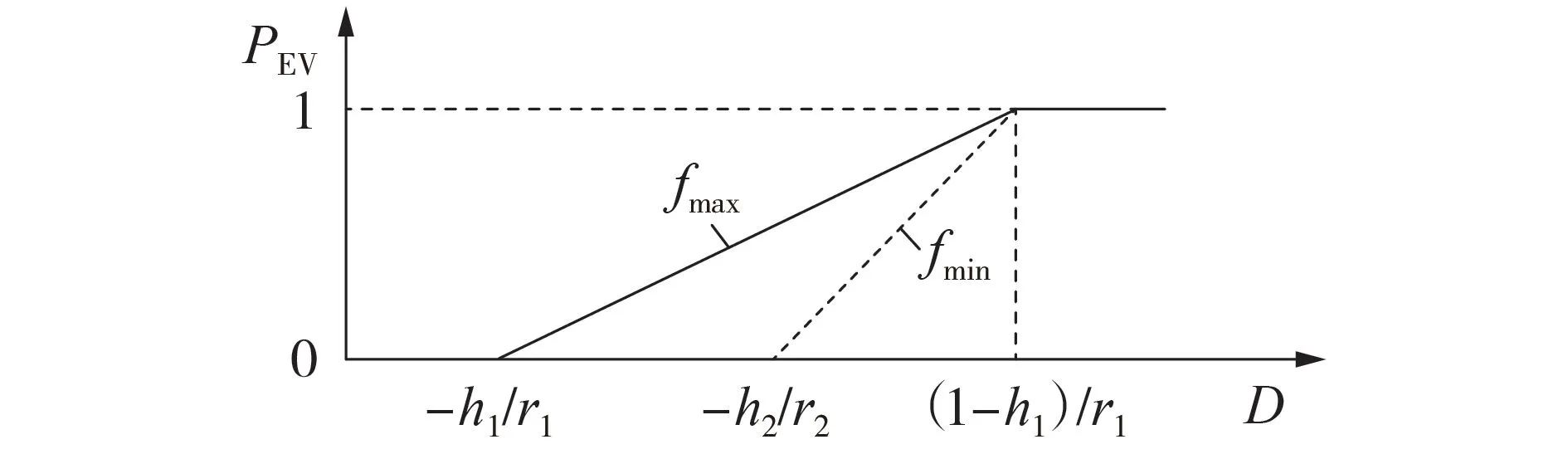
图1 基于EV车主响应意愿指标的参与调度的概率模型Fig.1 Probability model of participating in scheduling based on EV owner response intention index

2 EV有序充放电策略模型

2.1 EV有序充放电控制策略

本文的EV有序充放电控制策略如图2所示。

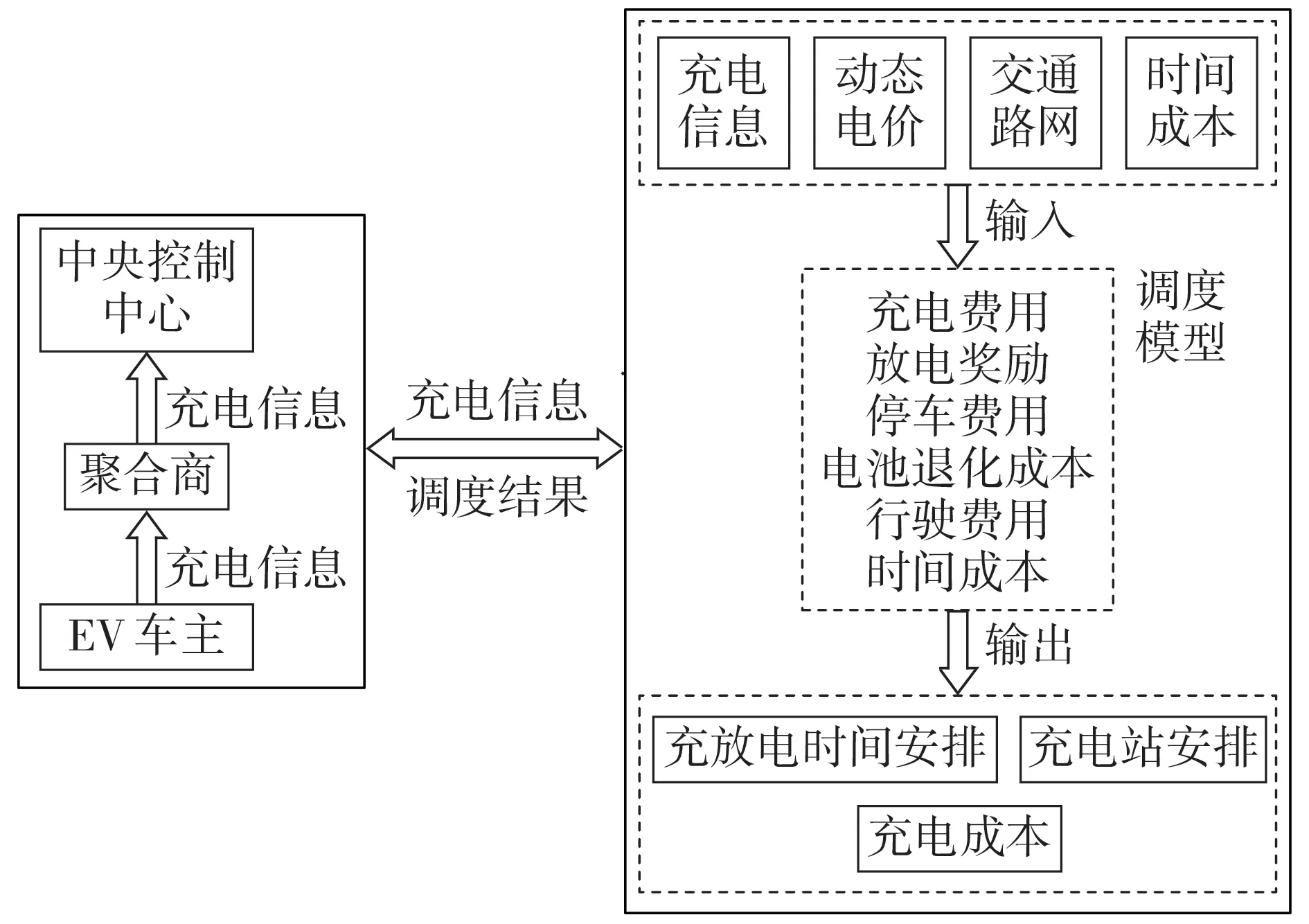
图2 EV有序充放电模型Fig.2 Orderly charging and discharging model of EV

首先，EV 车主通过人机交互界面设定预计离开时间、期望电量、初始荷电状态、电池容量、出行目的地、时间敏感度等信息，聚合商会将这些信息一同传至中央控制中心。然后，中央控制中心将信息进行汇总、处理，根据车主的出行链及各充电站实时的充电桩状态信息为车主计算最佳的充电站选择及其额外的行驶费用，并更新到站电池荷电容量。根据动态电价及车主设置的时间敏感度为其计算最佳的充放电时间安排，生成该车主的有序充放电策略。同时，也会为车主提供一个无序充电策略，无序充电策略会选取最近的充电站，且只进行充电。最后，中央控制中心会将2 种策略信息发送至聚合商，车主得到每种策略下的充电站安排、充放电时间安排（含充电完成时间）以及充电成本，车主可根据以上信息及自身情况进行线下响应。

2.2 目标函数

本文所提出的有序充放电策略的目标函数为EV 车主充电成本最小，包括EV 车主的充电费用、放电奖励、停车费用、电池退化成本、行驶费用以及时间成本，具体计算公式如下：

2.3 约束条件

本文约束条件包括EV 充放电状态约束、EV 调度状态约束、荷电状态上下限约束、荷电状态更新约束、充电功率和放电功率约束、建议离网时间约束及充电桩数量约束。其中，荷电状态更新约束、建议离网时间约束分别见式（9）、（10），其他约束条件见附录A式（A5）—（A10）。

3 算例分析

本文分别考虑了有序充放电模式及无序充电模式，并使用Lingo求解器进行求解。通过对比有序充放电模式与无序充电模式的充电费用、各区域内的充电负荷等信息，验证所提策略的可行性。

3.1 情景及参数设置

设定EV 到站时电池的初始荷电状态遵循［0.1，0.3］的均匀分布，同时EV 在与电网断开时车主所需的电池荷电状态为0.8，荷电状态的上、下限分别设置为1、0.1。本文中的动态电价及充电站购电电价来源于北京市EV市场，该电价的数据每15 min收集一次，鼓励放电的奖励电价为实时充电电价的90%，充电站购电电价为实时充电电价的60%。EV聚合商的分时电价等各项数据见附录B 表B1，目前各地方政策的停车费收费标准通常与充电电价成正比。取拟合参数q1=0.0001、q2=-0.0014、q3=-0.0425、q4=0.000 3、b1=0.8、b2=-1.6、b3=12。本文将EV 车型分为私家车、出租车、公交车及公用车，每种车型所对应的时间敏感性、出行特性及电池特性见附录A表A1—A3及附录B表B2。

本文采用某典型城区的交通拓扑结构见附录B图B1，该城区包括34 个节点、58 条支路、10 个住宅区H1—H10、6 个商业区B1—B6、5 个工作区W1—W5、5 个综合区Z1—Z5，路网数据见附录B 表B3，该地区的基础负荷见附录B图B2。

3.2 EV参与调度结果分析

EV 仿真数量N为1 000 辆，其中私家车数量占40%，出租车数量占30%，公交车与公务车数量各占15%，并对如下4 种情景下的仿真结果进行对比分析。

情景1（采用本文策略）：EV 采用本文所提有序充放电模式进行充放电，时间敏感系数有ω1—ω3这3 种情况，其值分别为0.05、0.2、0.4，N=1 000 辆。不同类型的EV 选取对应的ω，以此模拟多种类型EV的特性。

情景2：EV 采用本文所提有序充放电模式进行充放电，ω=0，N=1 000 辆。此时ω取0，即不考虑时间成本，则该情景下的EV将会过于积极地参与调度及进行放电，将其与情景1 进行对比，可分析引入时间成本的必要性与效果。

情景3：EV 采用本文所提有序充放电模式进行充放电，ω=0.4，N=1 000 辆。此时ω取0.4，即该情景下车主将承担很高的时间成本，将其与情景1 进行对比，可分析考虑多种类型EV时间敏感系数差异性的必要性及效果。

情景4：EV 采用无序充电模式进行充电，N=1000辆。

3.2.1 不同情景下时间负荷及经济性对比

1）情景1下4种车型充放电特性分析。

图3与图4分别为4种不同车型在情景1下的充电功率和放电功率。可见：私家车充放电时间随机性较强；公交车由于路线固定，排班时间固定，大多会选择在中午及夜间进行充放电；公务车的充放电时间则多集中在工作时间；出租车在任何时段均有可能进行充电，但因出租车司机的休息时间有限导致放电水平较低。图5 为该情景下1 000 辆EV 的总充、放电数量。

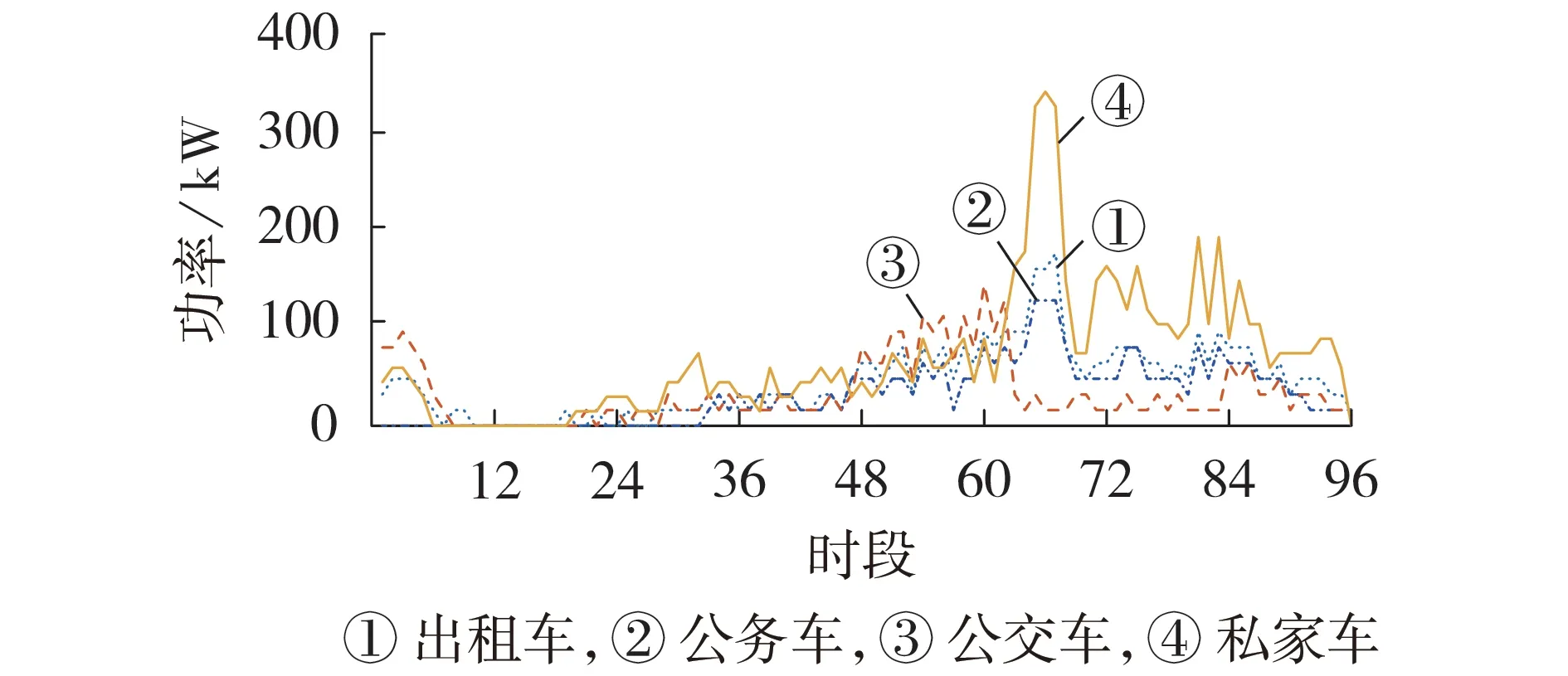
图3 情景1下4种车型的充电功率Fig.3 Charging power of four vehicle types under Scenario 1

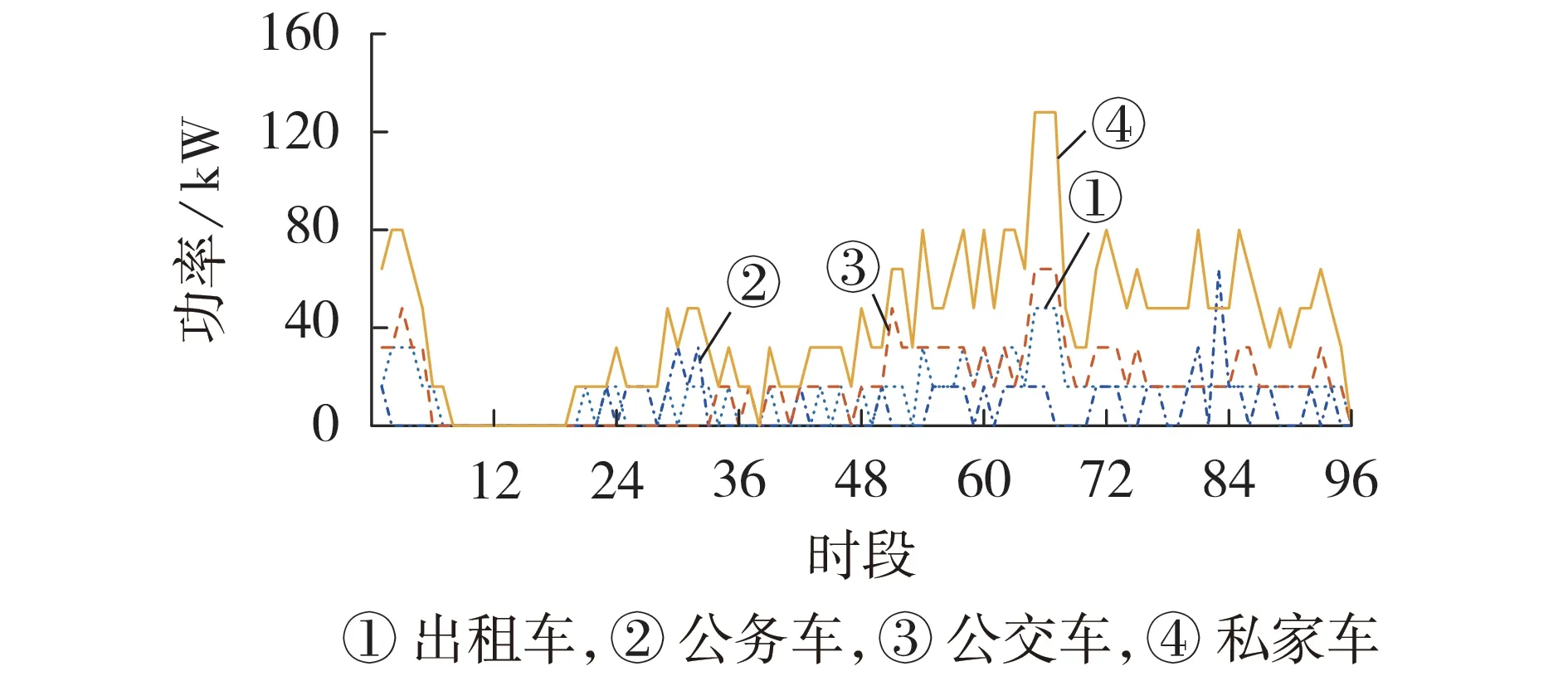
图4 情景1下4种车型的放电功率Fig.4 Discharging power of four electric types under Scenario 1

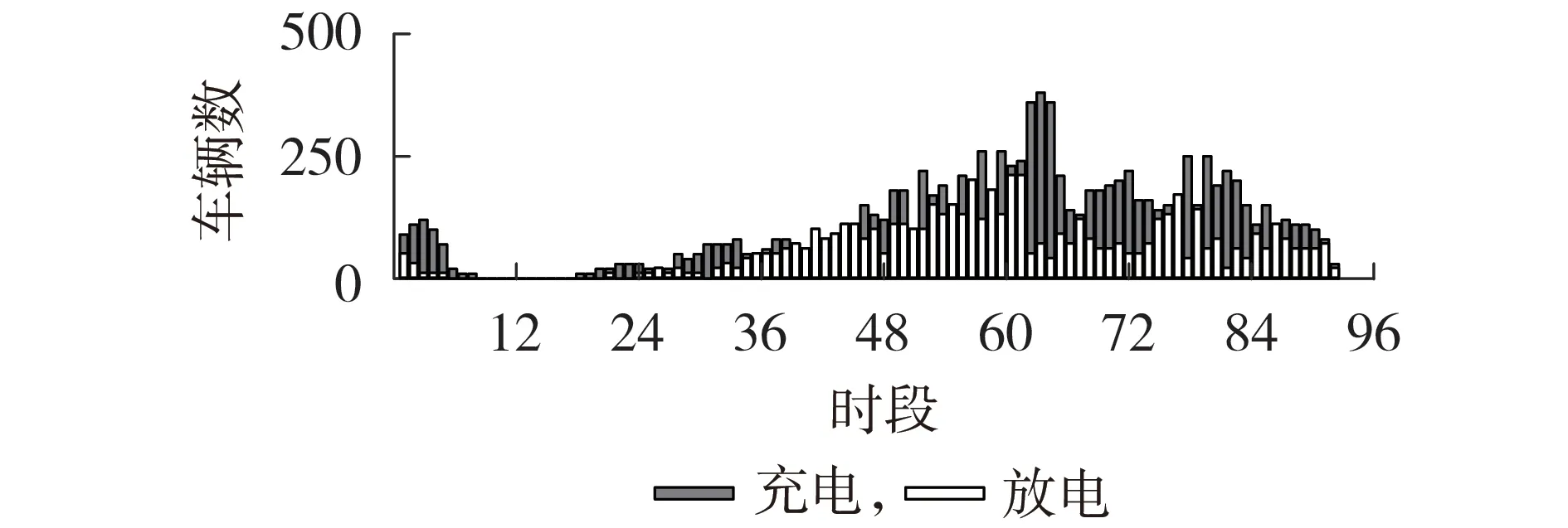
图5 情景1下1000辆EV的总充、放电数量Fig.5 Total charging and discharging quantity of 1000 EVs under Scenario 1

2）不同情景下的调度结果对比分析。

表1 展示了不同情景下的EV 参与调度的概率与综合放电率。由表可知：情景1 采用本文策略，此情景下EV 积极参与调度，有序地进行充放电，取得了良好的经济效益；情景2 中ω取0，此情景下所有EV 都忽略了时间成本，EV 过于积极地进行放电，经济效益良好，但安全性较差；情景3 中ω取最大值，由于时间成本过高，此情景下EV参与调度的概率较低，无法发挥有序充放电策略的作用，经济性差。4种情景下经济效益的仿真结果见附录B 表B4，结果表明采用本文策略后用户的充电成本降低，且充电站的收益升高，实现了经济上的共赢。

表1 不同情景下EV参与调度的概率与放电率Table 1 Probability of EV participating in scheduling and discharging rate under different scenarios

图6 展示了4 种情景下的电网总负荷曲线。由图可知：采用本文策略后，情景1 下的峰谷差相比无序充电模式下降了31%，实现了削峰填谷；情景2下参与放电的EV 过多，该情景虽然使峰谷差下降了27%，但在高峰结束后又产生了一个新的充电高峰，发生了负荷越界的现象；情景3 没有发挥出有序充放电策略的效果，峰谷差下降了14%，仍然发生了负荷越界的现象；情景4 采用无序充电模式，负荷越界严重，严重危害了电网的安全运行。

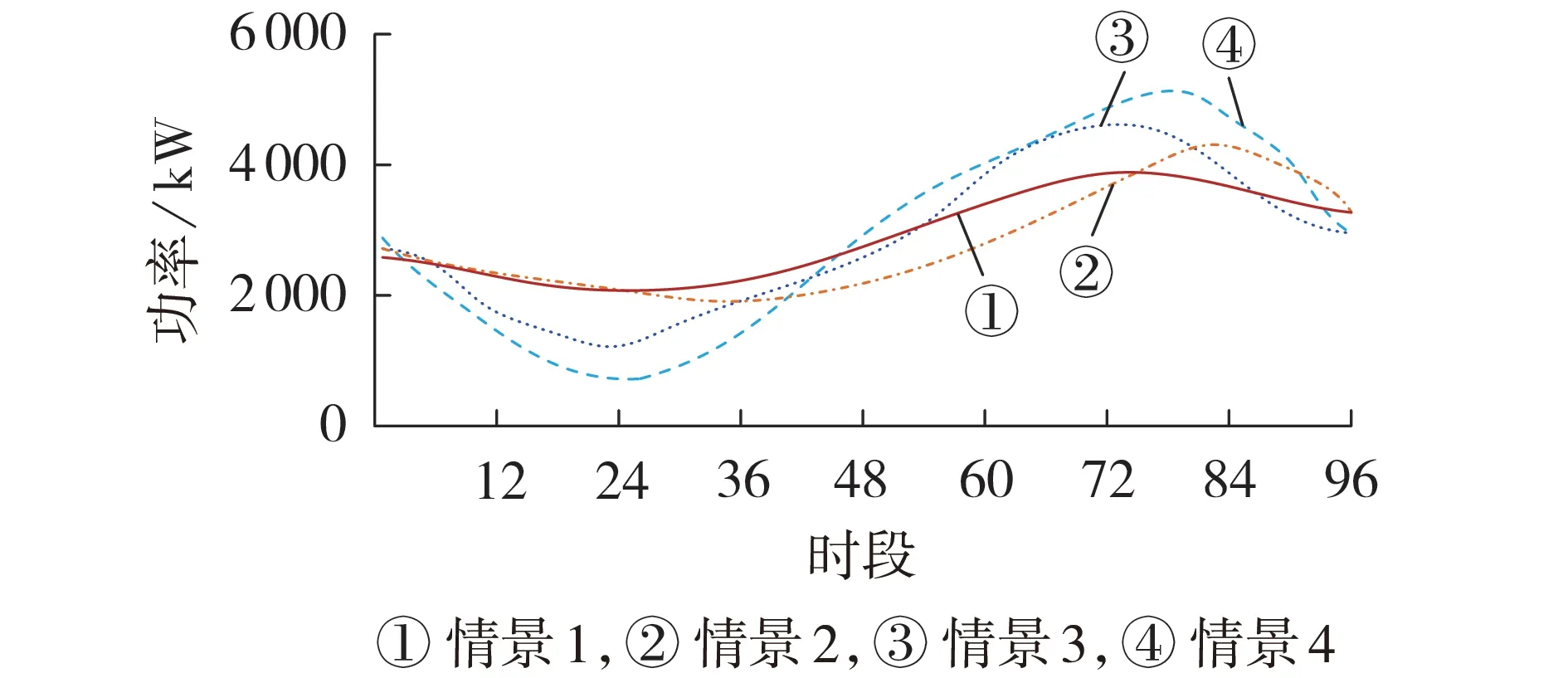
图6 不同情景下的负荷曲线Fig.6 Load curves under different scenarios

由上述结果可知，若调度中心在进行调度安排时忽略用户的时间成本（情景2），则车主会过于积极地参与调度和进行放电，仍然会形成一个用电高峰。而若在进行调度时选择一个过高的时间敏感系数且对所有车辆都选取同样的数值（情景3），则会使得车主不愿采纳有序充放电策略，达不到优化策略应有的效果。由上述对比分析可知，本文策略（情景1）考虑了用户的时间成本，同时针对不同车型选取了合适的时间敏感系数，更加贴合实际情况，具有较好的调度效果。

3.2.2 情景1与情景4的空间负荷对比

图7为情景1下各充电站的总负荷，可见在采用本文策略后，共有247 辆车接受了优化调度策略，前往了闲置充电站进行充电，在使自身充电费用降低的同时提升了区域内充电桩的利用率。图8 为情景4下各充电站的总负荷。可见由于节点14位于工作区，大量EV 选择在该节点进行充电，而由于节点2位于住宅区的边缘，只有少部分EV选择在该节点充电，使得该区域内的充电桩利用率较低，与此同时极大地提升了在节点14 进行充电的EV 的停车费用及时间成本。

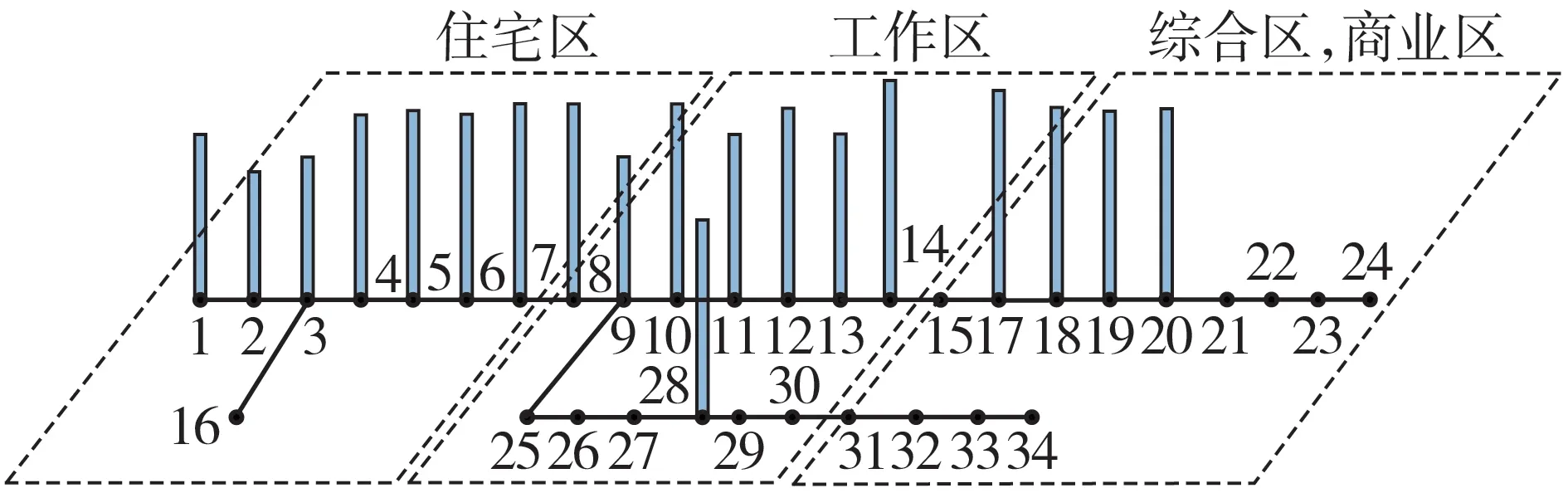
图7 情景1下各充电站的负荷Fig.7 Load of each charging station under Scenario 1

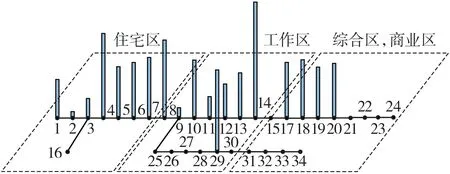
图8 情景4下各充电站的负荷Fig.8 Load of each charging station under Scenario 4

情景1 与情景4 下各充电站在各时段的充电负荷分别见附录B 图B3 和图B4。可见采用本文策略不仅降低了个别高峰充电站的负荷，还使得该区域内各充电站的负荷趋于平均，使区域内的充电桩利用率提升了18.3%，避免了负荷越界，提升了充电站的收益。

3.3 与其他文献对比结果分析

表2 给出了本文策略与其他文献所提策略的结果对比。表中：文献［14］考虑了电池损耗的问题，提出了考虑用户放电节制的调度策略；文献［15］以用户综合指标考虑了用户因素对充放电安排的影响，进而求解充放电安排。采用本文策略后，车主的充电成本降低了29%，同时，充电站的收益上升了35%，峰谷差降低了31%，充电桩利用率提升了18.3%，由此可见本文策略在有效降低车主充电成本的同时提升了充电站的收益，实现了经济效益上的共赢。此外，本文策略还实现了削峰填谷，有效地降低了峰谷差，提升了充电桩的利用率，缓解了电网的压力。

表2 不同策略的结果对比Table 2 Comparison of results among different strategies

4 结论

为了解决EV 时空特性的随机性较强及车主时间成本与满意度未被充分考虑的问题，本文提出了一种考虑不同车型EV时空特性及时间成本的EV有序充放电策略，并得到如下结论。

1）针对EV 时空特性的随机性较强、现有EV 出行模型不准确和难以模拟真实情况的问题，研究了不同车型、不同区域及不同道路等级对EV出行链的影响，建立了包含多种影响因素的EV时空负荷特性模型，使模型更加贴近实际情况。

2）在影响EV 充放电行为的因素中引入了时间成本，同时考虑了用户的响应意愿对其参与调度概率的影响，解决了传统优化策略中未充分考虑车主出行便利性的问题。推荐适合参与调度的车主前往闲置充电站、在合理的时间段内进行充放电，避免了区域内总负荷发生越限的危险，降低了个别高负荷充电站的负荷，提高了充电桩的利用率。

3）采用本文策略后，EV 车主的平均充电成本下降了29%，充电站的总利润提升了35%，充电桩的利用率提高了18.3%，同时实现了削峰填谷，在达到经济效益共赢的同时还有效提高了电网运行的安全性。

本文模型中的动态电价是根据历史数据进行设计的，若能使动态电价随负荷而改变，则可以进一步优化调度策略，后续笔者将对实时动态电价的设计进行研究。

附录见本刊网络版（http：//www.epae.cn）。