基于信息间隙决策理论与动态分时电价的电动汽车接入虚拟电厂双层经济调度策略

呙金瑞，张智俊，窦春霞

（1. 南京邮电大学 碳中和先进技术研究院，江苏 南京 210023；2. 南京邮电大学 自动化学院、人工智能学院，江苏 南京 210023）

0 引言

当前，能源危机与全球变暖问题日益显著，引起了人们的广泛关注［1］。虚拟电厂（VPP）是利用先进的通信技术与控制理论聚合大量分布式资源的虚拟发电厂［2］，在解决上述问题方面发挥了重要的作用。此外，VPP 通过内部的优化调控使大量开发的分布式电源（DG）、大规模推广使用的电动汽车（EV）等多种类型的分布式资源协调运行，实现其内部资源的有效分配。可见，VPP对节约能源、减少温室气体排放以及达成“双碳”战略目标具有重要的意义［3］。然而，DG 出力的间隙性［4］会导致系统发生功率波动，并增大VPP 调度的难度［5］。同时，随着EV 的大规模推广使用，EV 的无序充电行为也加剧了EV 聚合商（EVA）的调度难度［6］。因此，如何在考虑DG 出力间隙性与EV 无序充电的场景下使VPP 与EVA 协调以达到整体成本最优，是一个具有挑战性的问题。

目前，已有大量关于VPP优化控制、经济调度方面的研究。文献［7］采用集中控制结构实现VPP（包括热电厂、风电场、光伏电站）内部风电、供热设备的运行调度，但该控制结构会导致在优化过程中出现“维数灾难”问题。文献［8］提出了一种自下而上的VPP 分散控制方法，基于激励-响应控制策略对VPP中的光伏、EV、空调等灵活性设备进行优化控制管理。文献［9］基于多智能体结构建立了VPP 调度模型，采用完全分散控制方式对各分布式单元进行控制与调度。上述研究均针对“维数灾难”问题提出了很好的优化控制解决方法，但未考虑DG 出力的间隙性。文献［10］针对DG 出力的不确定性，提出了随机规划模型，并通过协调系统设备互补运行以最大化收益。文献［11］建立了以最小化系统总运行成本为目标的鲁棒优化调度模型，用于解决DG 出力的间隙性问题。文献［12］采用概率模型来描述DG出力的不确定性，并调节灵活负载以实现能量优化管理。然而，在上述研究中，VPP的优化调度仍存在如下问题：①在不确定性方面，随机规划会导致计算效率低、鲁棒优化调度结果过于保守等问题；②在需求响应方面，较少关注EV与柔性负荷。而在实际的运行过程中，EV 与柔性负荷都是重要的灵活性调节响应资源，所以在研究DG 出力间隙性的同时，考虑EV与柔性负荷的调度策略很有必要。

此外，已有研究考虑了EV 无序充电的EVA 优化调度问题。文献［13］针对大规模EV 无序充电的问题，基于分时电价（TOUP）提出了EV有序充电的方法，但只考虑了EV的充电行为。文献［14］采用静态TOUP 模型引导EV 进行充放电以提高EV 的灵活性，但不能动态划分各时段［15］，难以使EV 灵活参与系统调度，还可能发生大量EV选择夜间低价时段充电所导致的另一负荷高峰的现象。文献［16］提出了一种考虑电动出租车车网互动协同策略，以改善区域电网的可靠性，但仅考虑了电动出租车车主的收益。综上可知，EV的无序充电行为对系统的稳定、经济运行有重要的影响，但已有研究主要集中在仅考虑EV有序充放电管理的EVA 经济调度方面，而在EVA 与VPP间的协调优化调度方面仍缺乏充分的研究。

在我国“双碳”战略目标的背景下，为了缓解DG出力间隙性带来的系统功率波动及EV 无序充电行为导致的调度困难问题，本文从EVA 与VPP 协调优化运行的角度出发，提出了一种基于信息间隙决策理论（IGDT）与动态分时电价（DTOUP）的EV 接入VPP双层经济调度策略。首先，针对DG出力的间隙性问题，采用IGDT 鲁棒模型改善系统的稳定性；其次，为了提高EV的灵活性，提出了基于“车-路”信息融合驱动的EV充电模型，并设计了基于模糊隶属度函数的DTOUP模型与整体最优指标，以改善EVA与VPP 整体的经济性；然后，结合DTOUP 与“车-路”信息，构建了以EVA 与VPP 交互成本和EV 里程焦虑成本最小化为目标的EVA 优化调度模型；最后，通过算例仿真验证了所提策略的优越性，并详细分析了相关参数、指标对所提策略的影响。

1 VPP结构及模型

1.1 VPP结构

VPP 通常由多类型、多区域的分布式能源构成，通过聚合多种能源来有效地降低DG 给电网运行带来的风险，并充分利用DG 效益以提高自身的灵活性与经济性。本文主要考虑的VPP 结构如图1 所示，其包含不可控的发电单元（风电、光伏）、储能系统（ESS）、负荷单元（可平移负荷（SL）、可中断负荷（IL）、不可控的基础负荷（BL））及大量具有灵活性的EV 充电站。其中，VPP 通过管控中心对各聚合单元进行统一管理与控制。

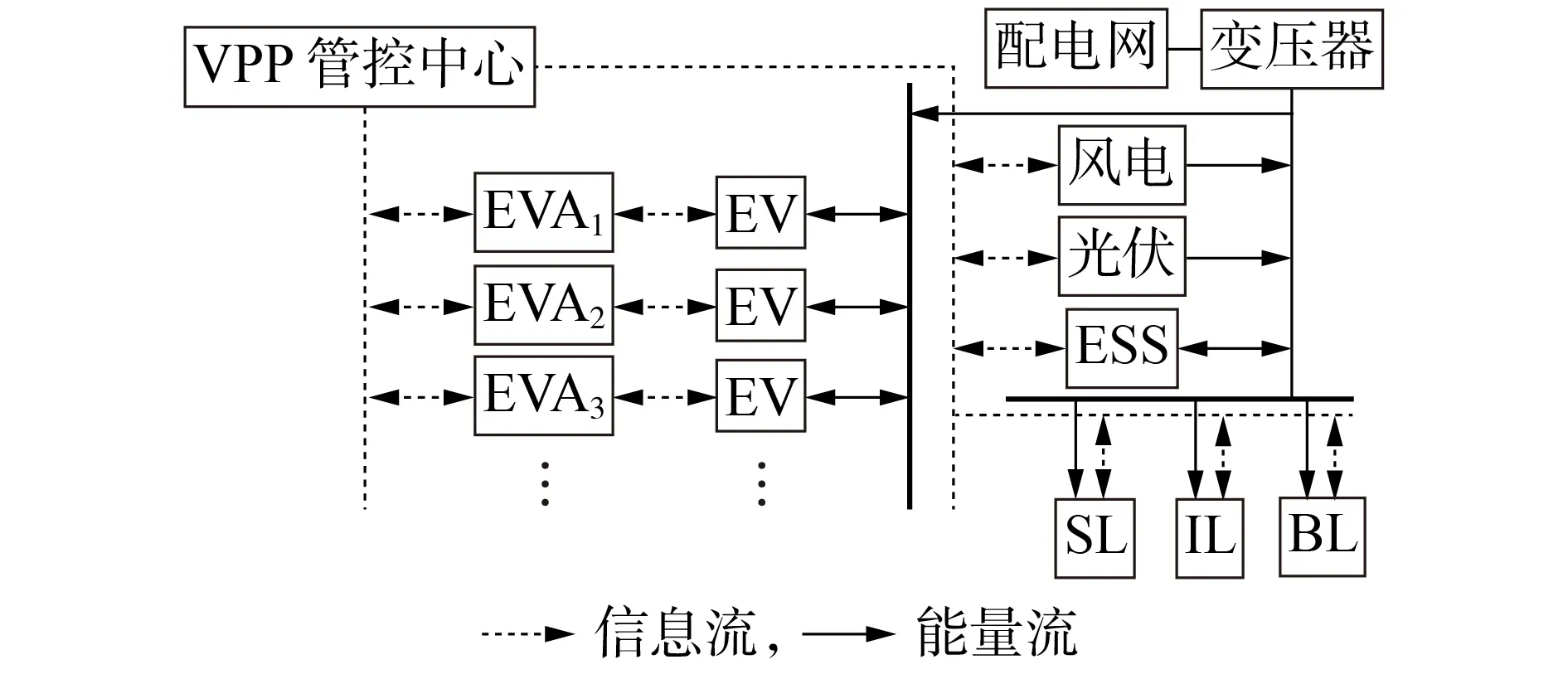
图1 VPP结构Fig.1 Structure of VPP

1.2 基于“车-路”信息融合驱动的EV充电模型

本文构建的基于“车-路”信息融合驱动的EV充电模型框架如附录A 图A1所示，该模型框架分为信息层、模型层、算法层3 层。首先，利用信息层生成模型层所需数据，模型层基于EV信息数据建立包含具体类型、驶入／驶出时刻等信息的EV 充电模型，并基于全球定位系统（GPS）信息数据构建交通道路模型［17］；然后，利用算法层的蒙特卡罗抽样方法生成一系列的EV 充电参数，并结合模型层中的速度-流量实用模型，根据最短行驶时间，确定EV 的最佳行驶路径；最后，基于所得充电信息进行反复抽样，确定EV的充电功率曲线。

1.2.1 交通道路模型

1）道路拓扑结构。

本文研究的道路拓扑结构如附录A 图A2 所示。图中，所有连接的道路均为双行道，充电站1—3 分别位于道路节点2—4 处。本文基于图论方法对道路拓扑进行说明［18］，令G(V，E)表示道路网，V为道路节点集合，E为道路集合，则道路网的邻接矩阵D如式（1）所示，节点g与节点k之间的道路长度dgk如式（2）所示。

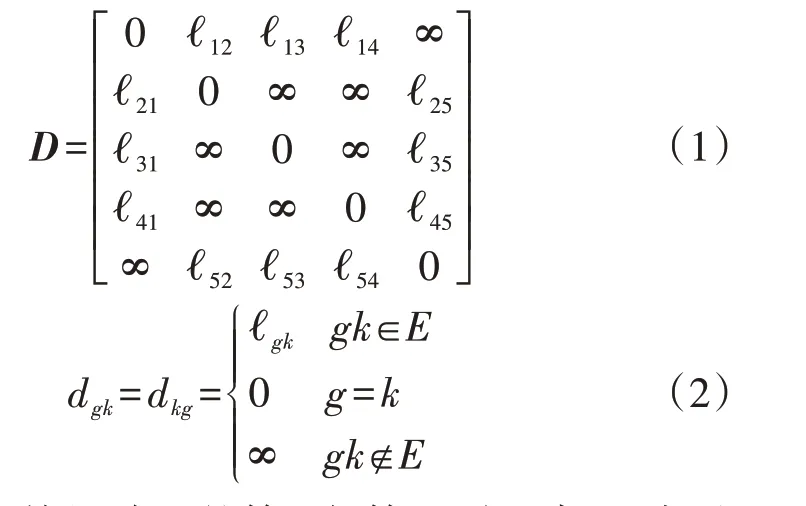
式中：ℓgk为邻接矩阵D的第g行第k列元素；∞表示两节点之间不相连。

2）速度-流量实用模型。

在道路网中，EV 的行驶速度会受到该道路容量与车流量的影响［19］。本文在研究EV 的行驶过程时，采用速度-流量实用模型对t时段EV 在道路gk上的车速vgk(t)进行描述，如式（3）所示。

式中：vgk，ff为道路gk的自由流速度；qgk(t)为t时段道路gk的车流量；egk为道路gk的实际通行能力，其大小与该道路的等级相关；qgk(t)/egk为t时段道路gk的饱和度；φ为关于qgk(t)/egk的非线性函数；m、n、ε为不同道路等级下的自适应系数［19］。

1.2.2 EV充电模型

1）EV类型。

依据不同功能EV 的出行特点，可将EV 划分为以下2类。

（1）电动出租车与非工作的电动私家车。它们的出行路线存在较大的随机性，且出行次数多，充电地点也相对不固定，时空随机性较大。

（2）其他类型的EV，如上班用的电动私家车、电动公务车及电动公交车。它们的出行路线较固定，充电地点也相对固定，时空规律性较强，因此本文不将其作为研究对象。

2）时空特性。

根据2009 年美国家庭出行调研数据，EV 行驶结束即开始充电时刻τ、日行驶里程d大致分别服从正态分布、对数正态分布［20］，其概率密度函数分别为：

式中：Wd，100为EV 行驶100 km 所需的电量；Pch为EV的充电功率；ηEVc为EV的充电效率。

根据上述模型，采用蒙特卡罗方法模拟EV日负荷并进行累加，可得到VPP 内EV 负荷的时空分布，并将其作为EV负荷的初始值代入双层调度模型。

1.3 DTOUP模型

考虑到EV 充电负荷受用户需求的影响而具有较大的充电时空随机性，为了充分发挥EV 的灵活性，以有效地实施充电站的充放电调度计划，本文基于模糊隶属度函数建立DTOUP 模型，即上层VPP 管控中心根据每天的负荷用电以及DG 出力情况，重新选取分时段的区域，并给下层EVA 制定该时段的电价。DTOUP模型的具体描述如下。

通过制定DTOUP，下层EVA 内的EV 用户可以根据电价进行灵活的充放电安排，选择在电价较低的时段充电，并在电价较高的时段放电，以降低用电成本。进一步地，上层基于下层反馈的充电计划，重新修改DTOUP。

1.4 柔性负荷模型

1.4.1 SL模型

VPP 中SL 的总用电量是一定的，且其在各时段的用电量是可灵活调整的。SL模型可以表示为：

2 双层经济调度模型

2.1 上层模型

2.1.1 目标函数

上层模型以最小化VPP 总成本为目标函数，其中VPP 总成本由VPP 与电网交互成本、需求响应补偿成本、VPP 与EVA 交互成本、ESS 运行维护成本组成。

1）VPP与电网交互成本。

考虑到VPP 在运行过程中会受到DG 出力间歇性等的影响而发生功率波动，可以通过向外部电网购售电以维持系统的功率平衡。t时段的VPP 与电网交互成本CVPPt可表示为：

式中：λSL、λIL分别为SL、IL的补偿系数。

3）VPP与EVA交互成本。

上层VPP经济调度的目标是在满足系统内各单元运行约束的条件下，通过对各聚合单元进行决策控制，使VPP总成本最小。则目标函数可以表示为：

2.1.2 约束条件

在VPP 的运行过程中，其内部各单元需要满足如下约束条件。

1）功率约束。

VPP 内参与维持系统功率平衡的单元包括ESS、DG、EV 和负荷单元，功率平衡约束如式（19）所示。此外，VPP 与外部电网之间联络线的传输功率不能超过其安全范围限制，即需满足式（20）。

3）柔性负荷约束。

柔性负荷约束如式（12）和式（13）所示。

2.2 下层模型

2.2.1 目标函数

下层模型以最小化EVA 内EV 用户总成本为目标函数，其中EV 用户总成本包括EVA 与VPP 交互成本和EV里程焦虑成本。

1）EVA与VPP交互成本。

VPP 制定DTOUP，EVA 内的EV 用户可以选择在DTOUP 谷时段充电，在峰时段通过放电以降低自身的充电成本。t时段的EVA 与VPP 交互成本C～EVt可表示为：

式中：γ为单位时间与里程费用的换算系数；ΔTgk为EV在道路gk上的行驶时间。

下层EVA 经济调度的目标是在满足EV 用户充电需求的条件下，根据上层VPP 制定的DTOUP 对EV 的充放电计划进行决策安排，使EVA 内的EV 用户总成本最小。则目标函数可以表示为：

2）EV电量约束。

在EVA 的调度过程中，为了确保EV 电量不会超过其电池容量，并保证在充电站结束充电时的电量能满足用户需求，需满足如下约束：

3 IGDT鲁棒模型

为了应对VPP 中DG 单元出力具有严重不确定性的问题，本文采用IGDT 对上层模型中的DG 出力不确定性进行建模。IGDT 是一种可以在不确定性因素的情形下有效对模型进行优化与控制的方法。IGDT 应对不确定性的机制如附录A 图A4 所示［22］，图中IGDT 包含了风险规避、机会寻求这2 个智能体。为了确定最佳决策变量，风险规避智能体最大化不确定性，而机会寻求智能体最大化目标函数值减少的机会以确定最佳决策变量集合。

本文采用包络约束对系统内DG 出力不确定性进行建模［22］，如式（35）所示。

4 模型求解

4.1 IGDT鲁棒模型的求解流程

由式（36）可知，该模型求解较困难，其解与DG出力的波动区间有关联，且波动区间也是模型求解的优化目标。由于这2 个问题之间存在相互联系，故需建立上层以不确定区间最大化、下层以VPP 总成本最小化为目标的双层优化模型［23］。附录B。

4.2 双层经济调度模型的求解流程

双层经济调度模型的求解流程图如图2 所示，具体步骤见附录C。

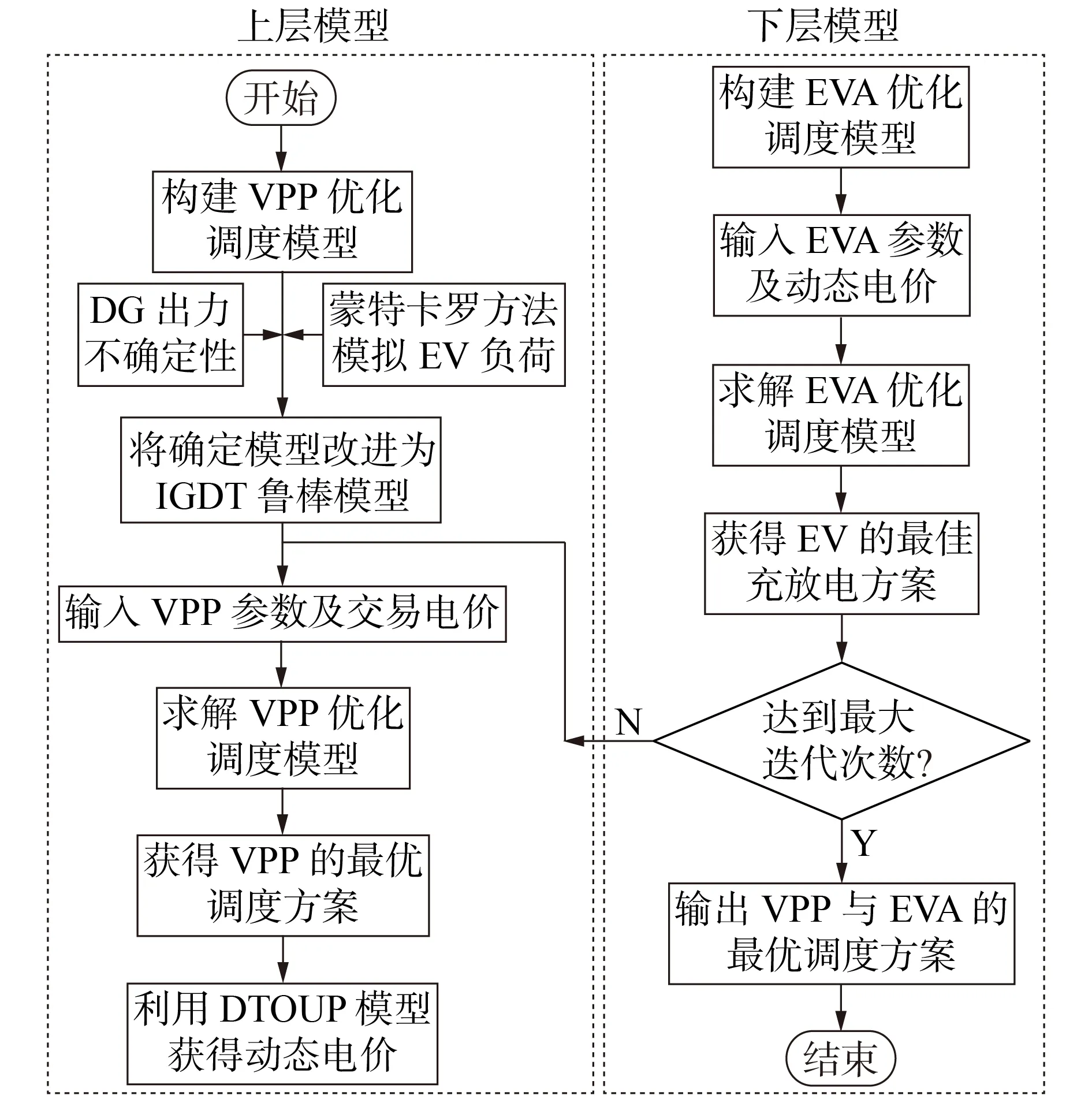
图2 双层经济调度模型的求解流程图Fig.2 Flowchart of solving bi-level economic dispatch model

4.3 整体最优指标

为了确定上层与下层的最优调度方案，本文定义了式（37）所示整体最优指标κ，其值越小，则整体优化效果越好。

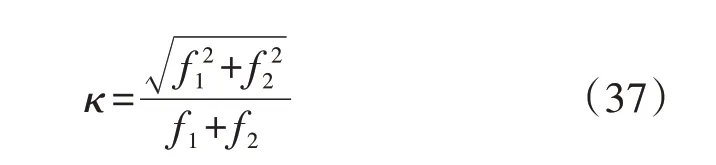
式中：f1、f2分别为上、下层的最优调度成本。

5 算例分析

5.1 算例说明

为了验证本文所提双层经济调度策略的有效性，基于图1 所示的VPP 架构进行仿真，并与TOUP模型进行对比分析。VPP 包含1 个发电单元、1 个储能单元、3 座充电站及负荷单元，TOUP 采用的是与电网交易的电价。为了进一步说明基于“车-路”信息融合驱动的EV充电模型的优越性，基于附录A图A2 所示的道路拓扑，将其与不考虑道路信息的情况进行仿真对比分析。

本文假设该区域共有40 辆电动出租车和80 辆非工作的电动私家车，且车辆均需从图A2中的节点1和节点5出发选择充电站进行充电。其中，设定电动出租车与非工作的电动私家车均可以多次放电，分别采用快速、慢速充放电方式进行电能交互，每座充电站均配有交流和直流充电桩。

5.2 EV充电负荷的时空分布

基于蒙特卡罗方法模拟EV 充电负荷［17，19］，仿真次数为1 000 次，仿真周期为24 h，且以1 h 为时段间隔将其分为24 个时段。每条道路上的EV 充电需求时空分布及仿真区域的EV 充电负荷总需求分别如附录D 图D1 和图D2 所示。各座充电站的EV 充电负荷曲线如图3所示。

图3 各座充电站的EV充电负荷曲线Fig.3 EV charging load curve of each charging station

由图D1 可知：在时间分布上，EV 充电需求呈现2 个高峰时段，分别为时段3 和时段12，这2 个高峰时段有充电需求的EV 数量分别为12、16 辆；在空间分布上，EV 充电需求分布不均匀，这是因为考虑到不同时段道路的拥堵状况不同，用户有时会选择路径更长的道路前往充电站进行充电，进而导致充电需求在空间分布上存在差异。

由图3 可知，EV 充电负荷呈现显著的“双高峰”特征，这是因为充电站1、2在高峰时段对电动出租车进行了快充服务。而在图3（b）中，充电站2的EV 充电负荷也呈现“双高峰”特征，这是因为前往充电站2 的道路1-3、道路5-3 为最短路径，在不考虑道路拥堵的情况下，有更多的电动出租车前往充电站2 充电，所以造成了“双高峰”现象。通过对比分析可知，本文在考虑道路信息的情况下避免了同一充电站出现“双高峰”充电负荷，有利于充电站的稳定运行。

由图D2 可以看出，电动出租车采用快充方式，使时段4 与时段13 出现了负荷高峰，充电负荷分别为337.50、296.25 kW。本文将该EV 充电负荷总需求曲线作为第1次迭代过程中的EV负荷初始值。

5.3 调度成本及整体最优指标对比

基于DTOUP 模型和TOUP 模型的上层VPP 总成本、下层EV 用户总成本和整体最优指标κ对比分别见图4 和图5。由图可知：DTOUP 模型所得整体最优指标结果比TOUP 模型的小；基于DTOUP 模型的上层VPP 总成本、下层EV 用户总成本在第2 次迭代时达到整体最优，而TOUP模型在第1次迭代时就达到了整体最优。但通过对比分析可知，本文所提基于DTOUP 模型的双层经济调度策略比基于TOUP模型的策略效果好。因此，下文的相关分析都基于DTOUP模型第2次迭代所得双层调度方案。

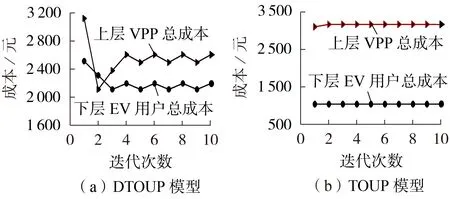
图4 不同电价模型下的成本对比Fig.4 Comparison of cost between different price models

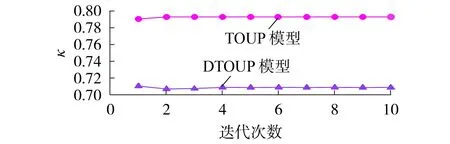
图5 不同电价模型下的整体最优指标对比Fig.5 Comparison of overall optimal indicator between different price models

5.4 调度优化结果

5.4.1 上层调度优化结果

不同电价模型下的上层调度结果对比见附录D图D3。由图可知，在本文所提DTOUP 模型下，VPP与电网的部分交互功率及ESS的部分充放电功率得到了提高，减少了负荷单元的功率调节。这表明DTOUP 模型对EV 充放电进行调整能使系统运行更加灵活。

5.4.2 下层调度优化结果

不同电价模型下的下层调度结果对比见附录D图D4。由图可知：EV 在DTOUP 模型下参与系统调度比在TOUP 模型下更加积极，避免了在系统负荷高峰时段进行集中充电；此外，基于DTOUP 模型，EV 用户选择在低价时段充电、在高价时段放电，这样不仅减少了自身的成本，还提高了VPP 整体的经济效益。

5.5 需求响应分析

上层柔性负荷的需求响应调度结果见附录D 图D5。由图可知，负荷在电价较低时段响应增加，在电价较高时段响应降低。柔性负荷参与需求响应减少了系统的调度成本，从而提高了系统运行的经济性。

5.6 偏差因子β的影响分析

为了研究不同偏差因子β的影响，首先设置β的取值范围为［0，0.2］，然后计算可接受的最大目标函数值f′，最后得到最大的不确定性区间α、双层调度成本及整体最优指标κ。

5.6.1β对α的影响

不同β取值下的α见图6。可见，随着β增大，α也增大。这是因为α增大，PDGt在U(α，P～DGt)内波动都可以使调度成本小于可接受的最大目标函数值f′。

图6 不同β取值下的αFig.6 α under different values of β

5.6.2β对双层调度成本及整体最优指标的影响

不同β取值下的双层调度成本及整体最优指标κ结果分别如图7 和图8 所示。由图可知，随着β增大，上层VPP 总成本与κ逐渐增大，而下层EV 用户总成本几乎保持不变，这主要是因为随着β增大，α也增大，决策者会考虑PDGt所导致的功率严重不平衡情况，致使需要更多的电能来保持功率平衡，进而导致上层VPP总成本增大。由于上层通过柔性负荷进行调节，使得系统的净负荷变化较小，因此DTOUP 模型对下层没有较大的影响，所以下层EV用户总成本几乎保持不变，但整体优化效果逐渐变差，故随着β增大，κ逐渐变大。

图7 不同β 取值下的成本Fig.7 Costs under different values of β

图8 不同β取值下的整体最优指标Fig.8 Overall optimal indicators under different values of β

5.7 IGDT模型的有效性分析

为了验证IGDT 模型处理PDGt不确定性的有效性，将其与文献［24］中的多场景分析法（MSAM）进行对比分析。IGDT 模型与MSAM 所得调度成本见附录D 图D6。由图可知，随着α增大，IGDT 模型所得调度成本也增大，而MSAM 所得调度成本几乎保持不变，且都显著大于IGDT 模型所得结果，这表明相较于MSAM，IGDT 模型更加符合实际情况。通过对比发现，IGDT模型的经济效益高于MSAM。

5.8 调度策略的计算时间分析

为了评估经济调度策略的实用性，附录D 表D1给出了优化流程迭代及整个优化流程的计算时间。由表可见，整个优化流程的总计算时间不超过5 min，且根据前文分析可知，第2 次迭代就产生了整体最优调度方案，所需时间不超过1 min。可见，本文所提策略可以在较短的时间内确定最优调度方案。

6 结论

本文考虑DG 出力的间歇性和EV 的灵活性，提出了一种基于IGDT 与DTOUP 的EV 接入VPP 双层经济调度策略。采用IGDT对DG出力不确定性进行鲁棒建模，基于模糊隶属度函数设计了DTOUP 模型与整体最优指标，在EV充电负荷模型中融合了“车-路”多源信息。基于算例仿真验证了所提调度策略的有效性，所得结论如下。

1）本文采用的IGDT 鲁棒模型总能得到比决策者制定的目标函数值小的调度成本，且相较于传统的MSAM，IGDT 鲁棒模型更加合理，经济性更高。同时，所考虑的需求响应模型提高了系统的供需平衡能力及经济性。

2）与传统的TOUP 模型相比，本文设计的DTOUP 模型可以更灵活地引导EV 进行充放电，使EVA 与VPP 整体的经济效益得到进一步提升。此外，所提整体最优指标κ能够更好地确定双层最优调度方案，使得调度策略更加合理。

3）考虑道路拥堵信息，本文所提模型避免了充电站的“双高峰”充电负荷，有利于充电站的稳定运行，EVA 能更合理地进行充放电规划。同时，从调度策略的计算时间结果可看出，本文所提策略可在较短的时间内确定最优调度方案以满足实际应用需求。

本文采用蒙特卡罗方法模拟EV充电负荷，其精度与计算速度还有待提高。此外，在EV充电模型中还存在复杂的多源信息。因此，采用改进的抽样算法模拟EV充电负荷以及在EV充电模型中考虑气候环境信息将是下一步的研究重点。

附录见本刊网络版（http：//www.epae.cn）。