RC构件承载力设计判据及双筋梁配筋方案研究
霍兵勇,杨毅哲,杨滨滨
(许昌学院 土木工程学院,河南 许昌 461000)
在进行钢筋混凝土(RC)受弯构件设计时,为了节约钢筋应尽量采用单筋截面,当截面弯矩设计值大于在单筋截面所能承受的最大承载力时,如果条件受到某种限制时可以考虑采用双筋截面形式进行设计;作为结构基本构件和最为常见的构件,无论在实际设计中,还是在结构性能研究中,与受弯构件设计相关的新问题依然存在,有待探讨的新问题及设计计算新方法不断出现.如梁柱节点处受弯设计公式的探讨[1],评估耐火性能时单筋梁的荷载比问题[2],复合材料加固梁的计算[3],规范[4]更新对双筋截面梁压区高度取值的影响[5]等等.高强钢筋轻骨料混凝土梁受弯刚度随钢筋用量增加而增加[6],双筋截面设计中因需要补充方程,多数情况是希望梁上部和下部受力纵向钢筋总的用量较少,因此假设压区高度为界限值或者最大配筋面积[7].结构设计最终目的是得到设计方案,即施工图,因此钢筋的选择、构件的延性[8]、构件的基本规定等因素需要在考虑之列,设计过程中双筋截面的承载力上限如何估计,双筋截面上部和下部钢筋选择时是否都要大于计算面积才满足承载力要求,对相关问题进行分析探讨.
1 单筋和双筋截面最大承载力估计
钢筋混凝土梁在设计过程中,如果弯矩设计值超过了单筋截面最大承载力,可以考虑采用双筋截面,双筋截面最大承载力如何估计有必要探讨,为了保证混凝土浇筑质量,规范中对钢筋净距有要求,即确定的截面宽度能放置的钢筋数量是有限的,依此推测双筋截面梁的承载力也有上限,为得到具体数值,在常规钢筋混凝土梁范围内讨论问题.
1.1 计算参数
选择混凝土强度等级C30,钢筋HRB400,钢筋直径和梁截面尺寸按表1数值计算,依据规范中梁内纵向钢筋数量、直径及布置的构造要求,截面上部和下部钢筋考虑最大放置数量,双筋截面受压区均考虑放置1层钢筋,受拉区放置2层钢筋,则常规几种尺寸的梁截面宽度的上部和下部钢筋配置列于表1.
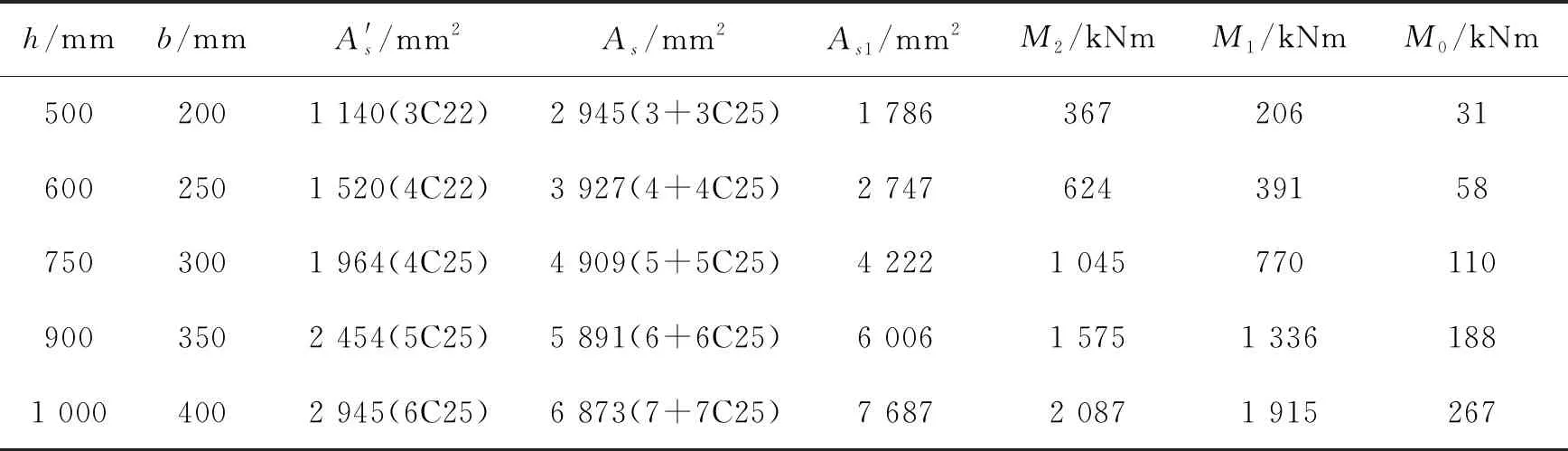
表1 梁底部放置2层钢筋时不同截面宽度对应的数值
考虑钢筋粘结和耐久性要求混凝土保护层厚度c取25 mm,箍筋直径取8 mm,计算得到的截面有效高度h0=h-as,每层钢筋净距25 mm,下部钢筋放置一层和两层时各工况下as值均为46 mm和66 mm.
1.2 单筋和双筋截面最大承载力
首先验算双筋截面情况下按表1配置梁上部钢筋,在下部钢筋放置2-4层时所得相对压区高度变化曲线见图1,曲线中相对压区高度大于0.518表示不满足适用条件,仅做对比参考,由计算结果可知:从满足界限压区高度这一要求来说截面宽度250 mm及以下的梁底部钢筋放置不宜超过2层,截面宽度300 mm及以上的梁下部钢筋可考虑放置3、4层.
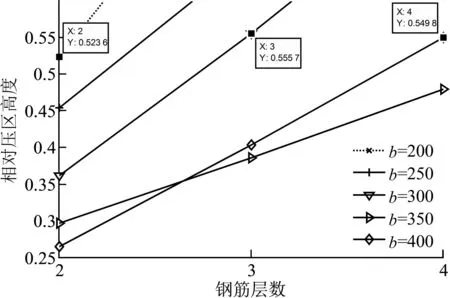
图1 相对压区高度随下部放置钢筋层数的变化曲线
其次比较单筋截面最小、最大承载力及双筋截面最大承载力,计算所得数值见表1.与下部2层钢筋放置数量最多时的面积比较可知:截面宽度300 mm及以下的梁按最大压区高度计算得到的最大承载力切实可行,截面宽度350 mm时理论计算钢筋面积已超过实配最大数量2%,理论上钢筋放置净距不满足构造要求,即:考虑受拉区放置2层钢筋时,350 mm及以上截面宽度应按钢筋放置数量最多来计算单筋最大承载力,或者考虑放置3层钢筋确保钢筋间距满足要求,此时最大压区高度代入式(1)所得弯矩值具有可行性,截面有效高度有所减小.
(1)
(2)
梁下部放置多层钢筋时,单、双筋截面依据实际情况计算最大承载力,单筋截面已知最大压区高度xb或下部钢筋面积As,双筋截面已知上部钢筋面积A′s和最大压区高度xb或上部和下部钢筋面积A′s、As.最大承载力随梁宽变化曲线如图2.
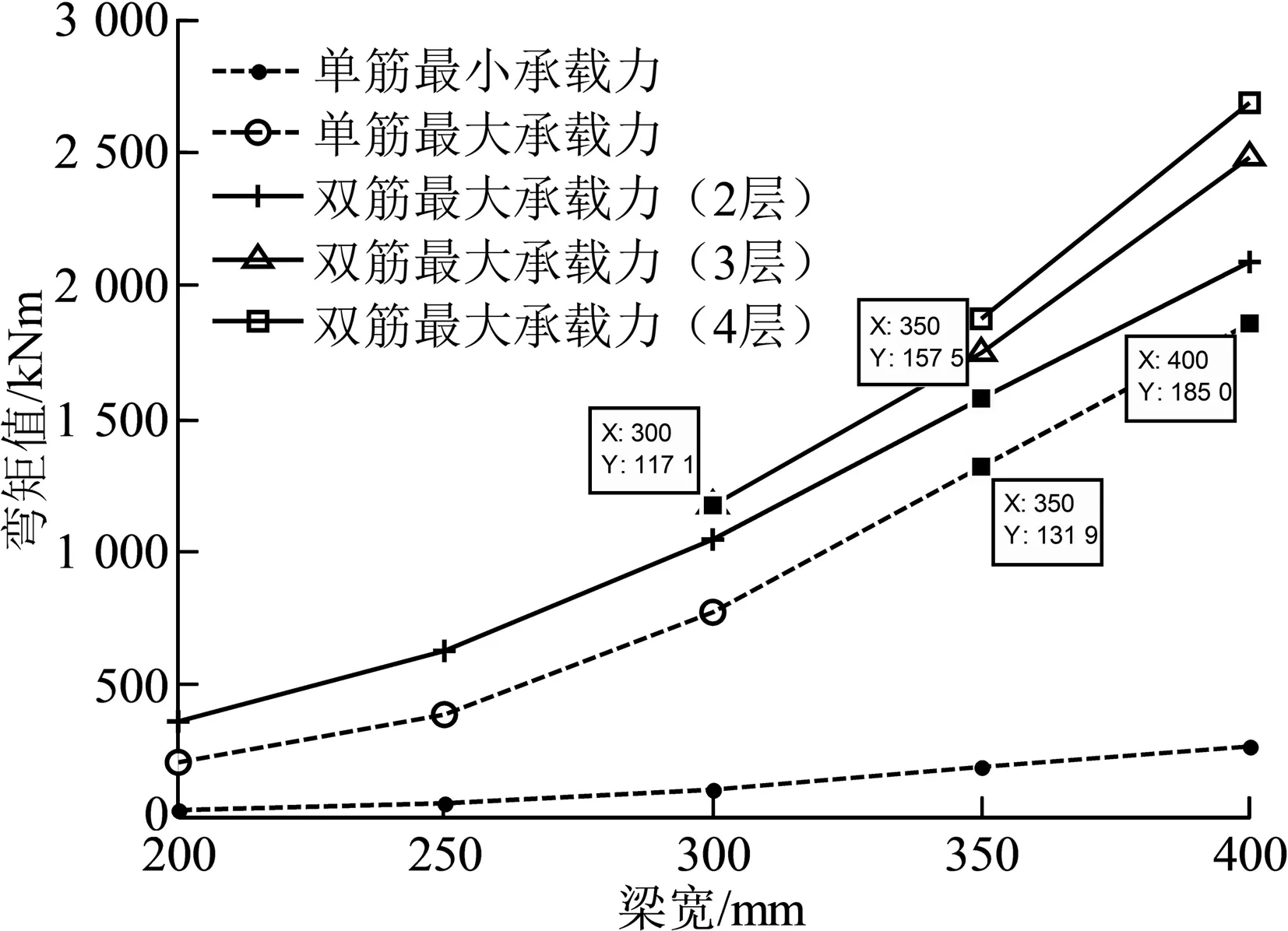
图2 单、双筋截面最大承载力随梁宽变化曲线
计算表明:确定截面宽度350 mm及以上单筋截面梁最大承载力时,需要考虑截面宽度、钢筋放置要求、钢筋层数等因素;双筋截面宽度350 mm和400 mm的梁下部钢筋层数增加弯矩承载力均增加,钢筋用量增加幅度更大.以35 mm宽度梁为例,放置钢筋3层与2层相比较底部钢筋面积多出16.6%,抵抗弯矩增加10%.400 mm宽度梁下部放置钢筋3层与2层相比较抵抗弯矩增加18%,但下部钢筋增加了28%,总体而言通过增加钢筋层数来提高承载力的方法其效率不高.
2 双筋梁钢筋用量与压区高度关系
由双筋截面梁设计计算公式且假设fy=f′y可以推导出梁上部和下部钢筋面积之和的表达式(3),同时可得受压区钢筋面积计算式(4)和受拉区钢筋面积计算式(5).
(3)
(4)
(5)
对式(3)的分析,压区高度x取最大值时钢筋用量最小为既成结论,进一步分析相关问题.以单筋截面最大承载力作为双筋截面时的最小承载力,则可得双筋截面承载力范围,弯矩M在此区间上取值可得钢筋总面积随相对压区高度的变化情况,式(3)方程右边除压区高度以外的其他参数均已知,弯矩M的每个确定值定为一种工况,则每种工况在x为最大压区高度时得到钢筋总面积值最小,其他压区高度或者说压区高度小于最大值时所得钢筋总面积比上最小钢筋总面积定义为相对用钢量,则相对用钢量随相对压区高度的变化曲线如图3.结果表明:压区高度越小,钢筋用量都不同程度增加,若由于延性、抗倒塌等需要不能取最大压区高度时,可以将相对压区高度控制在0.35,钢筋总面积增加量不超过10%.用钢量变化速度大于弯矩,如弯矩值增加38%,用钢量增加64%.

图3 相对用钢量随相对压区高度的变化曲线(梁宽350 mm)
不同弯矩值条件下上部钢筋面积和下部钢筋面积变化曲线如图4所示.梁上部钢筋减少,下部钢筋增加则相对压区高度和抵抗弯矩值都增大.上部和下部钢筋都增加的情况下若相对压区高度不变则抵抗弯矩值会增加,若相对压区高度减小则抵抗弯矩值有减小的可能,需要验算确认.
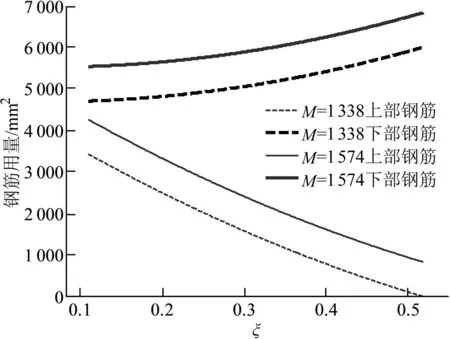
图4 上部和下部钢筋面积随相对压区高度的变化(梁宽350 mm)
由此可见,双筋截面设计时得到计算钢筋面积,下部实配钢筋面积大于计算面积,上部实配钢筋面积可小于计算面积,只要总量不减少则配筋结果偏于安全.
3 设计实例
已知矩形截面梁截面高度h=750 mm,宽度b=300 mm,混凝土强度等级为C30(其中,fc=14.3 N/mm2,ft=1.43 N/mm2),纵向受力钢筋采用HRB400级钢筋(fy=360 N/mm2),环境类别为二类,若梁截面的弯矩设计值M=860 kN·m,试设计梁的截面强度.(提示:钢筋一排时as=45 mm,双排时,as=65 mm).
解答:
(1)分析已知条件
截面尺寸,混凝土强度等级,钢筋强度等级,弯矩设计值分别为:b×h=300 mm×750 mm,C30,HRB400,Mu=860 kN·m.
(2)计算该工况下关键弯矩值
单筋截面最小承载力、最大承载力(按下部放置双层钢筋考虑)及双筋截面最大承载力(按构造要求在梁上部和下部放置的钢筋最大面积考虑).
①最小配筋率时所得弯矩承载力为M0
最小配筋率取
ρmin=max{0.2%,45ft/fy%},即max{0.2%,0.179%},取ρmin=0.2%,此时As=ρminbh=450 mm2,
②最大承载力为最大压区高度时的抵抗弯矩M1
此时受拉区钢筋按双层考虑,则
此时计算所需下部钢筋面积为4 222 mm2,双排放置可行.
③双筋截面最大承载力M2
选择钢筋C25按梁上部一排,下部两排钢筋放置,最大钢筋面积分别是1 964 mm2,4 909 mm2,则

(3)依据弯矩设计值Mu和关键弯矩值关系判断后续计算内容
可能的情况:情况1:Mu≤M0,按最小配筋率放置钢筋;情况2:M0 (4)把上述计算数值绘制到坐标轴上判断比较 比较易得计算结果符合情况3,可按双筋截面设计,需要补充方程,相对压区高度取上界限值可得到最小钢筋用量,若考虑塑性要求时相对压区高度可取上限值0.25或0.35,分析中相对压区高度值ξ取不同假定值所得计算钢筋面积列于表2. 分析:实际配筋仍需要按实际钢筋用量验算.如要求ξ上限值0.25,可在表2中ξ=0.2计算结果上选择钢筋尝试,上部钢筋计算面积超过截面内最大放置钢筋数量,可选择最大放置数量,即上部钢筋实际面积1 964 mm2,与计算面积相比少了207 mm2,需要下部钢筋实际面积大于3 801 mm2+207 mm2=4 008 mm2,选择3+5C25(3 927 mm2),钢筋总面积略少于计算值,但是上部钢筋面积减少,下部钢筋面积增加使压区高度和截面承载力均增加,因此仍有满足要求的可能性,验算后满足要求. 表2 计算钢筋面积 (1)计算单筋和双筋截面最大承载力需要考虑截面宽度、钢筋放置要求、钢筋层数和相对压区高度等因素的影响,尤其截面宽度大于350 mm的受弯构件. (2)通过计算分析单筋截面最小承载力、最大承载力及双筋截面最大承载力等关键弯矩值,可以为设计和优化等工作过程中的计算步骤提供有效导向判据,快速得到合理的方案. (3)双筋截面在配置钢筋时,下部实配钢筋面积大于计算面积,上部实配钢筋面积可小于计算面积,只要总面积不减少则配筋结果偏于安全. (4)采用双筋截面、增加钢筋层数来提高承载力的方法其效率不高,不经济.
4 结论

