多智能体系统的领导跟随一致性分析

李美霞

(天津城市职业学院 基础部，天津 300250)

到目前为止，许多研究者已经从很多不同的视角去研究了一致性问题,比如在文献[1-4]中,研究了系统存在时滞的情况.在文献[5]中,分析了具有马尔科夫链性质的随机时滞的系统的一致性,通过引入随机时滞的转移概率矩阵,降低了控制协议的保守性.在很多实际问题中,信息传输的过程中不仅存在时滞,而且不可避免地存在一些不确定性的因素,在文献[6]中,孙元功就研究了同时存在时变时滞和不确定性的多智能体系统的一致性分析.文章主要研究了在离散系统中,同时存在具有马尔科夫链性质的时滞和领导跟随的多智能体系统的一致性问题,通过创建一个合适的李雅普诺夫函数,根据图论的一些知识得到领导跟随一致的充分性.

1 模型描述

首先,给出马尔科夫链的一些相关定义.

定义1如果对于所有的m,i,j,有P(Xm+1=j|Xm=i)=P(X1=j|X0=i),则在状态空间S中,马尔科夫链X是均匀的.

转换矩阵Π=(πij)是 |S|×|S|的矩阵,其中πij=P(Xm+1=j|Xm=i),

转换矩阵Π满足

(1)

假设1时滞{dk}来自于有限的整数集合Γ={τ1,τ2,…,τq}并且满足 0≤τ1<τ2<…<τq.

考虑一阶系统的n个多智能体,其系统的每个多智能体的表达式为：

(2)

领导者的系统方程为：

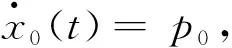
(3)

其中ui(t)是控制输入,且

(4)

令εi(t)=xi(t)-x0(t)，i=1,2,…,n, 则

(5)

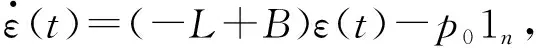
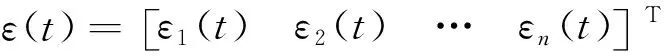
(6)

下面进行采样设置,则多智能体系统可以表示成下面这种离散的形式：

ε(k+1)=ε(k)+h(-L(dk)+B(dk))ε(k-dk)-hp01n

(7)

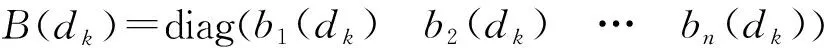
令H(dk)=h(-L(dk)+B(dk)),则(7)可写成以下形式：

ε(k+1)=ε(k)+H(dk)ε(k-dk)-hp01n

(8)

定义2如果

那么系统(8)是均方稳定的.

2 一致性分析

定理1对于带有具有马尔科夫链性质的随机时滞的系统(8)来说,在假设1和定义1的情况下,如果存在矩阵P>0,Qj>0,Zj>0,Mj和H(τj),j=1,2,…,q，使得下面的矩阵

(9)

对于任意的r=1,2,…,q成立,那么系统达到均方稳定,即所有的智能体跟随领导者达到一致.

其中

(10)

Ψi(r)=πriPH(τi)，

证明：设V函数为：

V(k)=V1(k)+V2(k)+V3(k)

其中

V1(k)=εT(k)Pε(k)

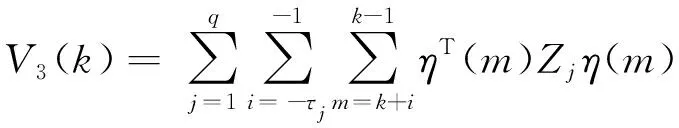
其中

η(m)=ε(m+1)-ε(m)

对于V3(k),根据(8),我们可以得到

令dk-1=τr,dk=τs,r,s∈{1,2,…q},从dk-1到dk的转换概率是：

P(dk=τs|dk-1=τr)=πrs

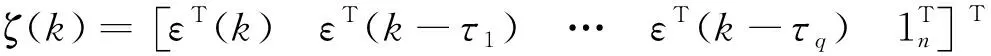
下面分别计算E{ΔV1(k)},E{ΔV2(k)},E{ΔV3(k)}

E{ΔV1(k)}=E{V1(k+1)-V1(k)}=E{εT(k+1)Pε(k+1)-εT(k)Pε(k)}=

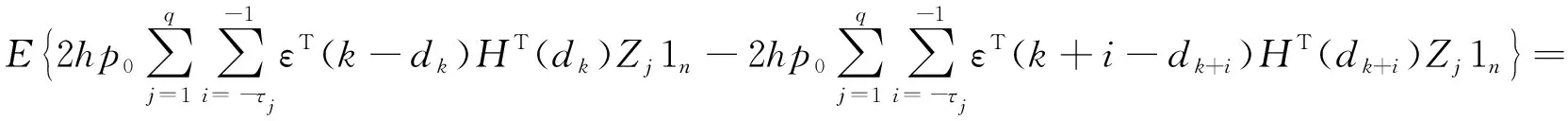
所以

E{ΔV(k)}=E{ΔV1(k)}+E{ΔV2(k)}+E{ΔV3(k)}≤

因为(9)成立,所以根据Schur补定理,我们可得

假设-λmax(r)I≤λ(W(r))≤-λmin(r)I,λ(W(r))是W(r)的特征值.

λmax(r)>0,λmin(r)>0分别是-W(r)的最大和最小特征值,

令β=min{λmin(r),r=1,2,…,q}>0,所以

E{V(k+1)-V(k)}≤ζT(k)W(r)ζ(k)≤-λmin(r)‖ζ(k)‖2≤-β‖ζ(k)‖2

然后将上式从0到k加起来得到：

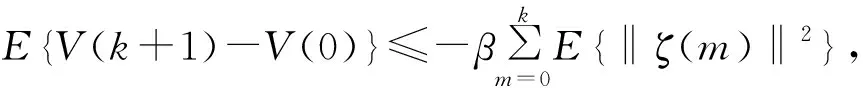
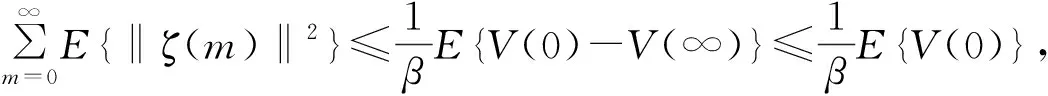
又因为‖ζ(m)‖2≥‖ε(m)‖2,m=0,1,2,…

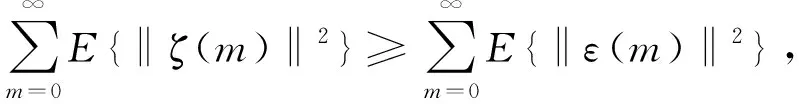
因此可得

所以系统(8)是均方稳定的,即所有的智能体跟随领导者达到一致.

3 小结

这篇文章研究了带有马尔科夫链的随机时滞多智能体系统的领导跟随一性,通过创建一个合适的李雅普诺夫函数,根据图论的一些知识得到领导跟随一致的充分性.文章最主要的特点是考虑了领导者的因素,除此之外这篇文章还有待更深的提高,如提高系统的维数，增加多个领导者等等.一般情况下,一致性得到的都是线性矩阵不等式，但此研究得到的是非线性矩阵不等式,如何将非线性不等式化成线性不等式还有待继续研究提高.