正六边形斜拉索风雨激振抑振机理及减振效果分析
吴金团,王 剑,戚永圣,周宗仁
(天津城建大学 土木工程学院,天津 300384)
斜拉索风雨激振是目前公认的对斜拉索桥危害最大的一种破坏形式,风雨激振指在特定风速下发生的较大幅度和较低频率的振动现象[1].斜拉索风雨激振现象普遍存在,世界上许多国家都出现过斜拉索桥因风雨激振破坏的现象,如中国洞庭湖大桥、杨浦大桥等[2].当时由于国内外缺乏关于斜拉索桥的有效减振措施,导致部分斜拉索桥遭到了不同程度的破坏.
空气动力学减振措施是目前最经济且减振效果较好的一种减振措施[3],在工程应用中也比较广泛.其中,在拉索表面缠绕螺旋线[4]、黏贴纵向肋条[5]、施加椭圆环[6]、压花[7]、压凹坑[8]以及采用多边形拉索截面是最为常见的几种空气动力学减振方式.Kobayashi等[9]采用多边形拉索截面作为试验研究对象,发现多边形拉索截面波浪起伏的外形能有效抑制拉索的风雨激振现象.Kleissl等[10]通过在圆形拉索表面黏贴规则凸起物进而变为正六边形的拉索外形,发现其有一定的减振效果。
目前各国研究人员认识到上水线的形成和振荡是斜拉索发生风雨激振的主要原因[11-13].由于钝体斜拉索的风洞试验还不成熟,需要与数值模拟结合起来共同研究水膜在钝体拉索表面的流动情况.多边形拉索截面的抑振机理并不十分明朗,还有待进一步的研究.关健、乔浩玥建立了可用于分析任意拉索截面的风雨激振理论和计算模型[14-15].本文在他们研究的基础上,将拉索截面设置为正六边形.在COMSOL软件中建立正六边形斜拉索截面模型并计算出拉索表面各个点位处的风压力系数和风摩擦力系数,将计算出的风场系数导入到MATLAB软件中运用有限差分法求解拉索振动和水膜运动方程.笔者从拉索振幅,气动升力,拉索表面水膜形态变化,上水线振荡区间内水膜厚度时程变化以及上水线振荡规律这五个角度全面分析正六边形截面拉索风雨激振的抑振机理和减振效果.
1 计算模型
1.1 模型介绍
参照Li等人做的圆形拉索风雨激振风洞试验模型[16],基本参数与该试验设置一致,并在乔浩玥[15]等人建立的可用于分析任意拉索截面模型的基础上,本文建立正六边形的拉索截面模型来进行计算研究并同时计算了圆形拉索截面的工况用以进行对比分析.
将正六边形拉索的六条边视作六个索面,相邻两个索面的夹边视作棱边.为研究气流方向对拉索振动的影响,设置正六边形斜拉索气流正对棱边模型为工况一,气流正对索面模型为工况二,工况说明如图1所示.
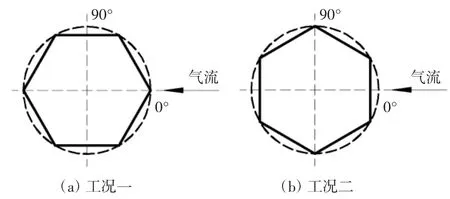
图1 工况说明
应用COMSOL软件建立正六边形斜拉索截面钝体绕流模型,设定正六边形拉索截面外接圆直径为D,坐标原点定位于拉索中心处.计算区域为30 D×20 D尺寸的矩形,斜拉索中心与入口1和入口3等距且距离入口2为12 D,距离左侧出口为18 D,计算风场示意如图2所示.
为消除边界条件带来的影响和保证计算结果的精确性和流畅度,对拉索附近的网格进行局部加密和尖角钝化处理,整个流场网格和正六边形拉索截面附近网格划分情况如图3和图4所示.
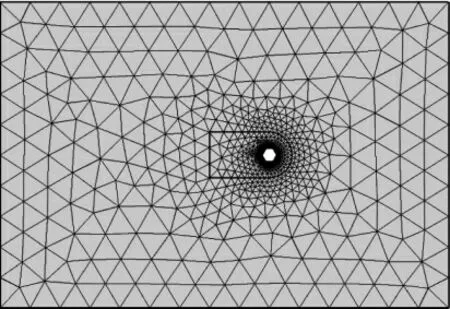
图3 流场网格划分示意
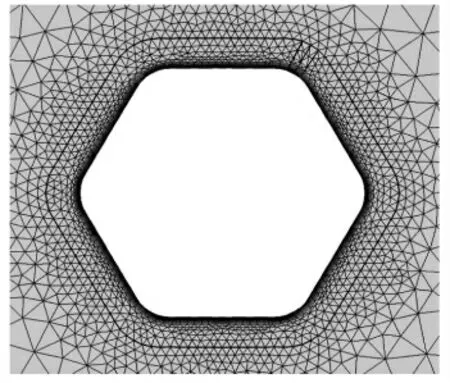
图4 正六边形拉索截面附近网格划分示意
1.2 计算流程
首先用COMSOL软件建立正六边形截面斜拉索的钝体绕流模型,并在该软件中进行拉索表面风压力系数Cp和风摩擦力系数Cf的求解计算.然后将计算结果导入到MATLAB计算程序中,采用有限差分法对水膜运动方程进行数值求解,可以得到水膜厚度和拉索表面气动升力等参数,在此基础上进行拉索振动方程的求解,可以得到拉索的振动位移、速度、加速度等参数,将加速度代入下一个时间步的水膜运动方程中进行迭代计算,计算流程如图5所示.
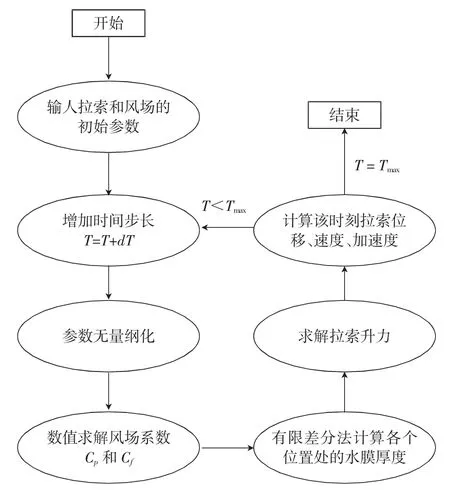
图5 计算流程
2 计算参数
参照Li[16]等人在风洞实验室利用超声波测厚系统在人工降雨条件下测量拉索表面水膜厚度的风洞试验,为确保水膜的连续流动设定初始水膜厚度为h0=0.25 mm,最小水膜厚度设定为hmin=0.02 mm,时间步长dT=0.001 s.正六边形拉索外接圆半径为0.05 m,考虑到正六边形拉索截面的几何特性,为方便建模计算,将正六边形斜拉索截面沿周边环向离散为120个点,并在COMSOL中建立极坐标系,横纵坐标分别为Rcosθ,Rsinθ.其横截面示意如图6所示.其他计算参数参照风洞试验[16]参数(见表1).
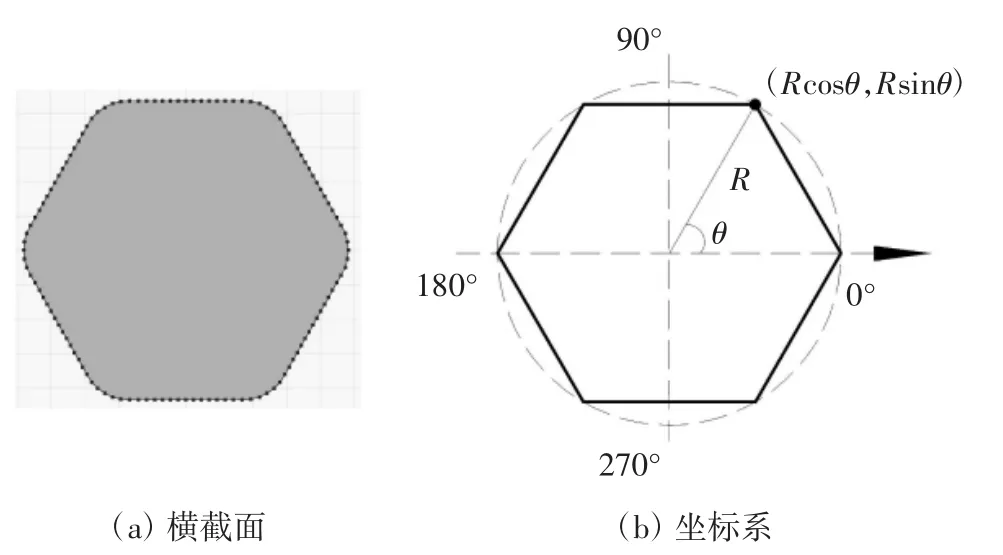
图6 正六边形拉索横截面示意
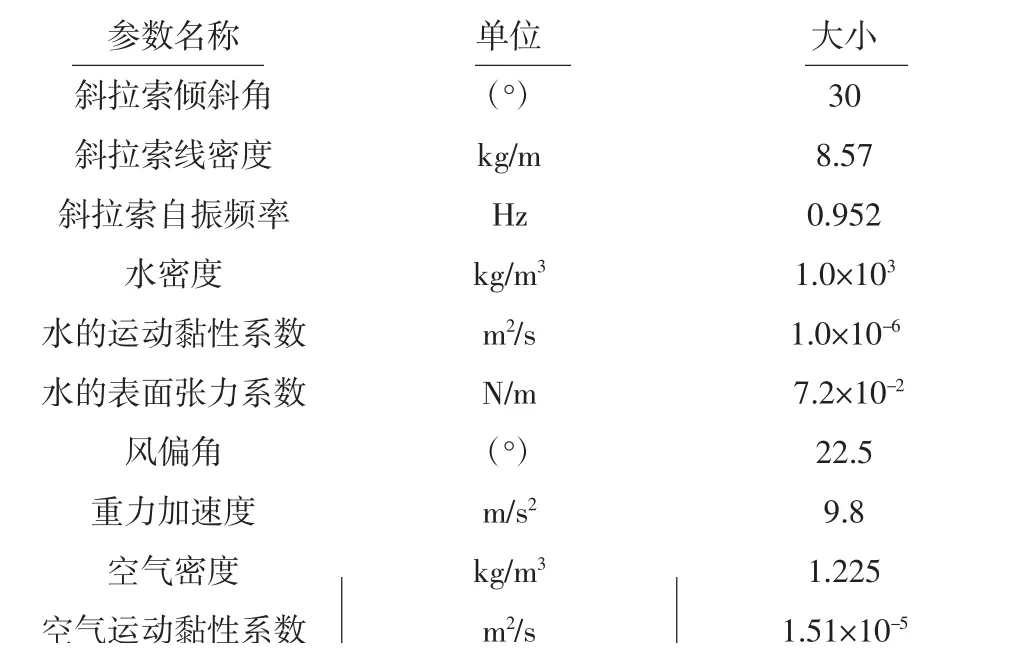
表1 其他计算参数
3 计算结果
为了验证数值模拟计算的准确性并方便与正六边形拉索的计算结果进行对比分析.参照Li等[16]做的圆形拉索风洞试验,试验中当风速设定为7.72 m/s时风雨激振现象最为激烈,所以选择该风速作为对比风速.
3.1 拉索振动响应
图7显示的是0~30 s圆形拉索的振动时程曲线及频谱分析.从图中可以看出斜拉索开始时刻的振幅是0.025 m,逐渐增大到25 s时基本达到稳定,并且25~30 s处于相对稳定状态.平均振幅为0.088 m,与试验得到的结果0.09 m极为接近[16].振动主频为0.999 Hz,与风洞试验得到的拉索自振频率0.952 Hz很接近[16].
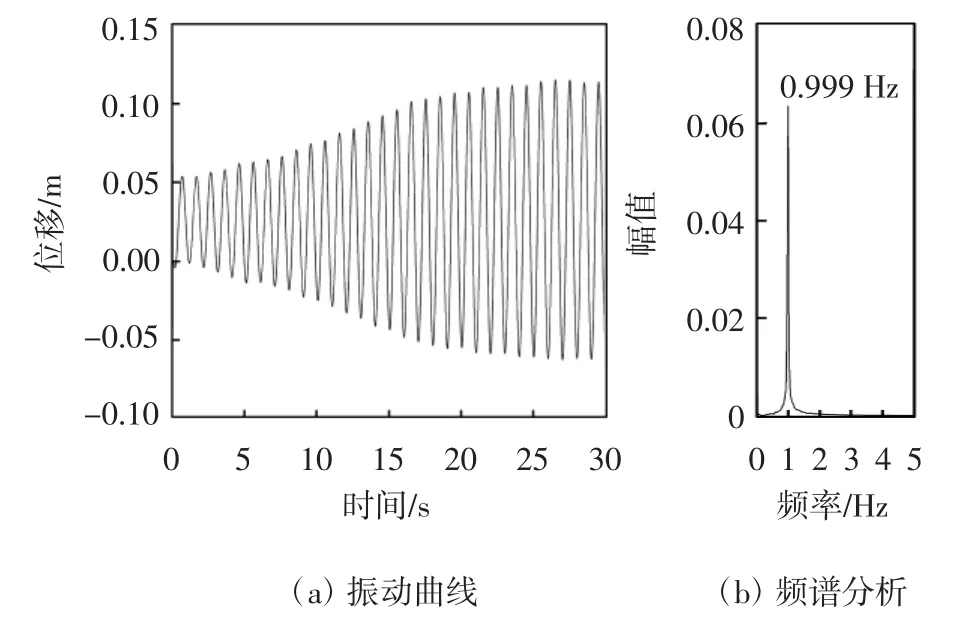
图7 圆形拉索截面振动时程曲线及频谱分析
图8显示了正六边形拉索在气流正对棱边工况下0~30 s的振动时程曲线及频谱分析.从图中可以看出,拉索的平衡位置从开始位置沿重力方向下移,在y=-0.033 m附近达到平衡位置并发生周期性振动.在0~23 s内拉索振幅由刚开始的0.031 m逐渐增大,在23 s时拉索振幅增大为0.05 m,23~30 s振幅保持相对稳定.频谱分析显示拉索振动主频为0.994 Hz.
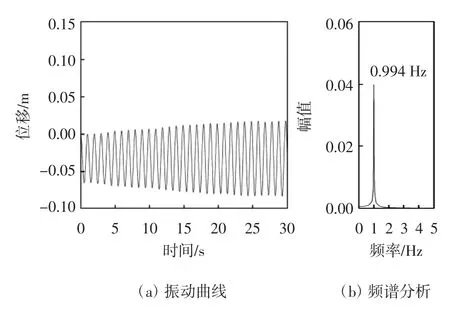
图8 工况一拉索振动时程曲线及频谱分析
图9显示了正六边形拉索在气流正对索面工况下0~30 s的振动时程曲线及频谱分析.振动时程曲线显示拉索平衡位置也从开始位置沿重力方向下移,在y=-0.034 m附近达到平衡位置并发生周期性振动,这一平衡位置与气流正对棱边工况的平衡位置极为接近.在0~5 s内拉索振幅由刚开始的0.038 m逐渐减小;在5 s时拉索振幅减小为0.033 m;5~15 s内振幅保持相对稳定然后在15~25 s内振幅又逐渐减小;在25 s时拉索振幅减小为0.031 m;25~30 s内振幅保持相对稳定.频谱分析显示拉索振动主频为1.003 Hz.
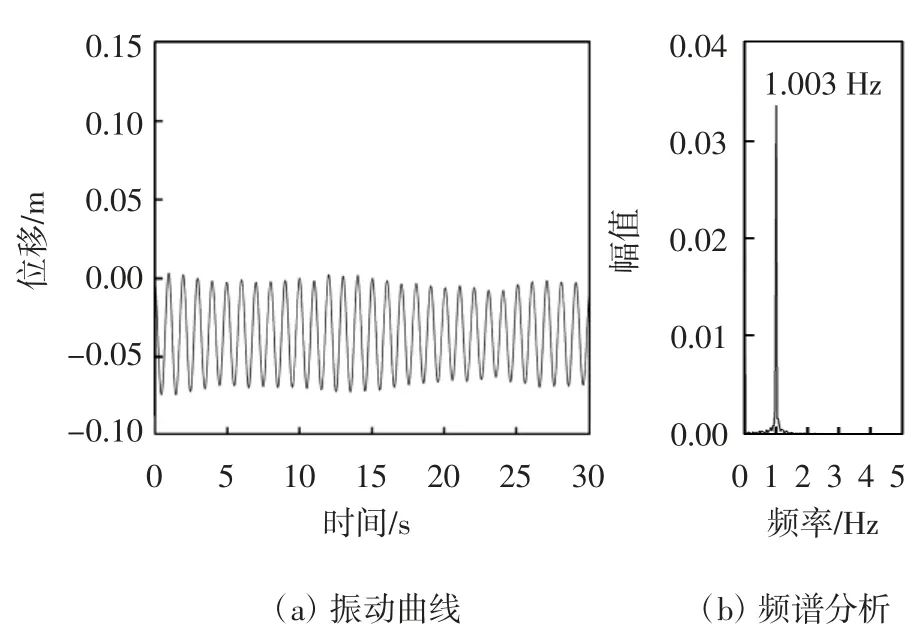
图9 工况二拉索振动时程曲线及频谱分析
表2显示了圆形拉索与正六边形拉索的振动特性对比分析情况.从表中可以看出气流正对棱边工况下正六边形拉索的减振幅度为43.2%;气流正对索面工况下正六边形拉索的减振幅度为64.8%.由此说明不论风从哪个角度吹向正六边形拉索,振幅都得到了明显减小,并有效抑制了斜拉索风雨激振现象.当气流正对索面时减振幅度更大,即当风速方向与正六边形拉索索面垂直时减振效果较明显.

表2 拉索振动特性对比分析
3.2 拉索气动升力
为了便于与正六边形拉索的升力变化情况进行对比分析,现列出了圆形拉索的气动升力时程曲线及频谱分析,如图10所示.时程曲线显示,在0~25 s内,升力变化范围逐渐增大,然后在25~30 s内保持相对稳定并在0.051~1.704 N内发生周期性变化,差值是1.653 N.频谱分析显示,拉索升力变化主频为1.008 Hz,能量幅值大小为0.232,接近拉索自振频率0.952 Hz,说明了拉索表面气动升力的周期性变化导致了拉索振动的周期性变化[13].
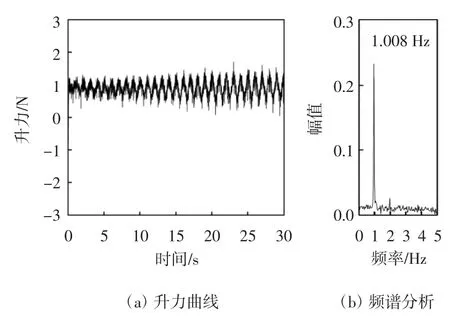
图10 圆形拉索气动升力时程曲线及频谱分析
图11显示了正六边形拉索在气流正对棱边工况下0~30 s的气动升力时程曲线及频谱分析.时程曲线显示,拉索升力在0~23 s内变化范围呈现出略微增大趋势,然后在23~30 s内稳定下来并在-1.504~-0.894 N范围内发生周期性变化,差值是0.61 N.频谱分析显示,升力变化主频是0.999 Hz,能量幅值大小为0.170.
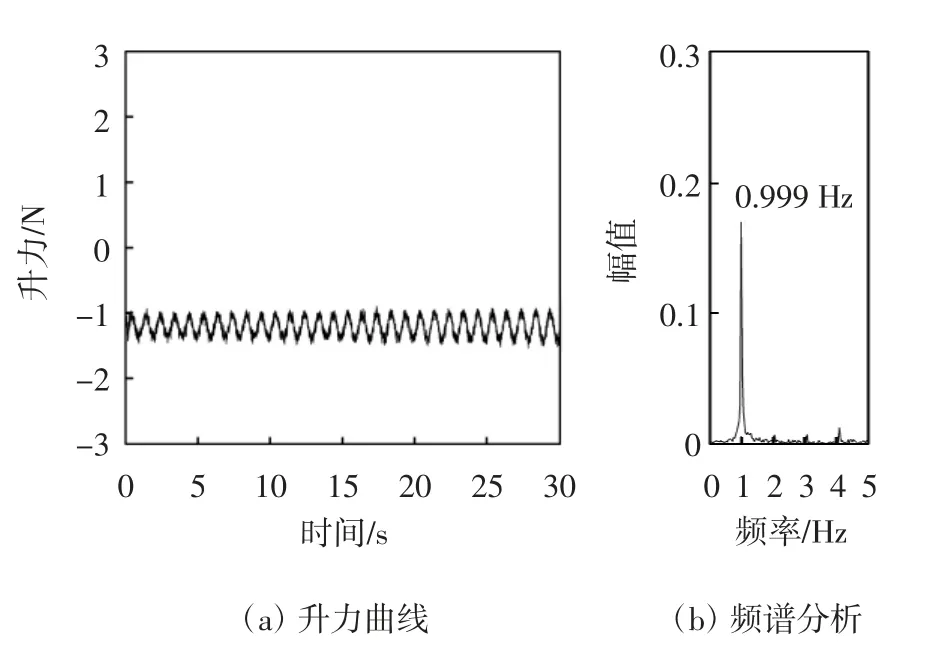
图11 工况一拉索气动升力时程曲线及频谱分析
图12显示了正六边形拉索在气流正对索面工况下0~30 s的气动升力时程曲线及频谱分析.时程曲线显示,拉索升力在0~25 s内的变化范围是-2.043~-0.735 N,差值是1.308 N.在25~30 s内的变化范围是-1.8~-0.831 N,差值是0.969 N.变化范围呈现出减小趋势.频谱分析显示,拉索升力变化主频是0.998 Hz,能量幅值大小为0.121.
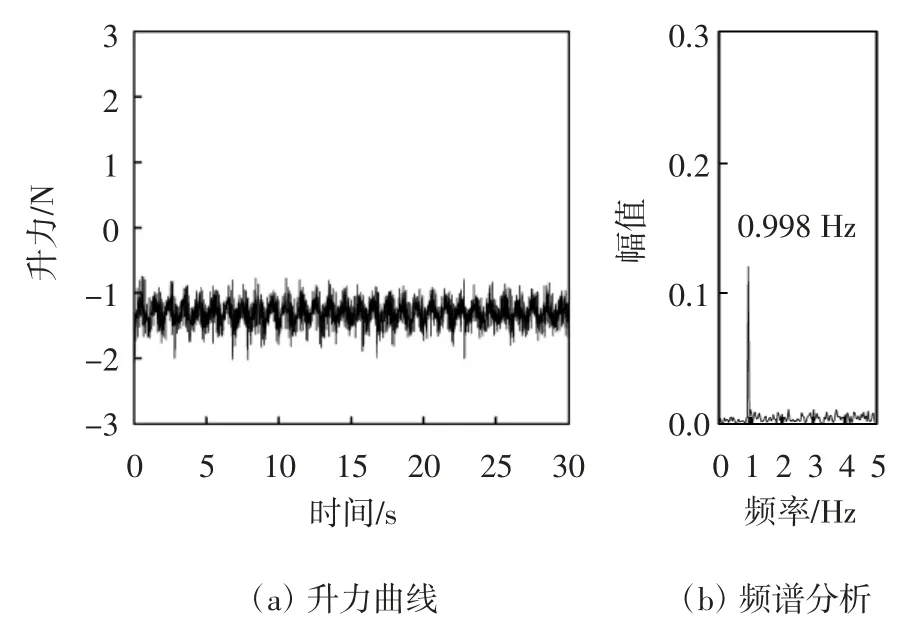
图12 工况二拉索气动升力时程曲线及频谱分析
表3显示了圆形拉索与正六边形拉索的气动升力特性对比分析情况.从表3中可以看出正六边形拉索的两个工况相比圆形拉索升力方向发生了改变并且当气流正对索面时,气动升力的绝对值更大,这与Kleissl等人做的气流方向对正六边形拉索气动力系数影响的试验研究结果相一致[10].对比圆形拉索计算结果,气流正对棱边工况下正六边形拉索气动升力主频能量幅值降低26.7%,升力变化差值减小63.1%;气流正对索面工况下正六边形拉索气动升力主频能量幅值降低47.8%,升力变化差值减小41.4%.说明正六边形拉索在不同气流方向作用下升力变化的周期特性都得到了明显的减弱从而导致拉索振动大幅削弱.
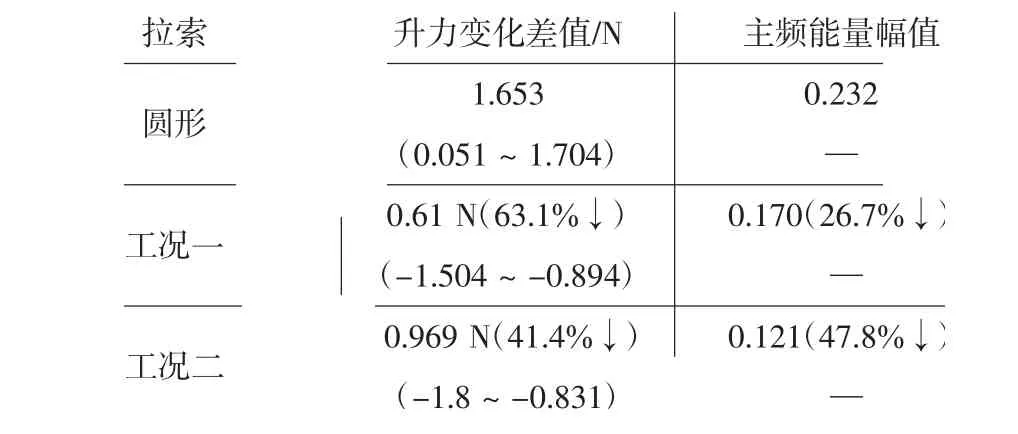
表3 拉索气动升力特性对比分析
3.3 拉索表面水膜形态变化
图13显示了0~30 s圆形拉索表面水膜形态的变化情况.从图中可以看出,下水线水膜厚度虽然很大但是周期性流动的现象非常微弱,而上水线约在31°~80°之间发生了明显的周期性流动和振荡现象,水膜最大厚度约为0.4 mm,水线宽度约为42.76 mm且变化不大.这一现象与数值模拟[14-15]和风洞试验观测结果[16]相一致.下水线在刚开始的时候就出现了明显的积聚现象并在θ=274°~286°范围内发生周期性振荡,水线宽度约为10.47 mm.θ=279°是水膜积聚现象最明显的位置点,厚度达到了1.1 mm.从图13中还可以看出上水线存在着下滑流动的痕迹并且在下水线振荡区间上边缘附近的水膜厚度非常薄,说明了上水线附近的水在重力、摩擦力、风作用力、水膜内部张力作用下主要是从迎风侧流向下水线的[14].上水线的水膜流动情况如图14所示,图中实体箭头表示上水线在迎风侧的流动方向,图中阴影箭头表示上水线在背风侧的流动方向.
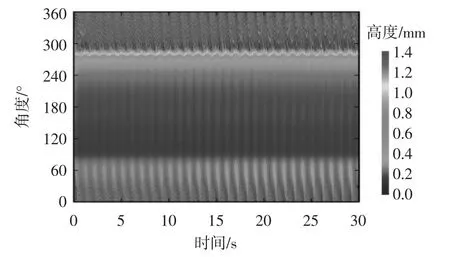
图13 圆形拉索表面水膜形态
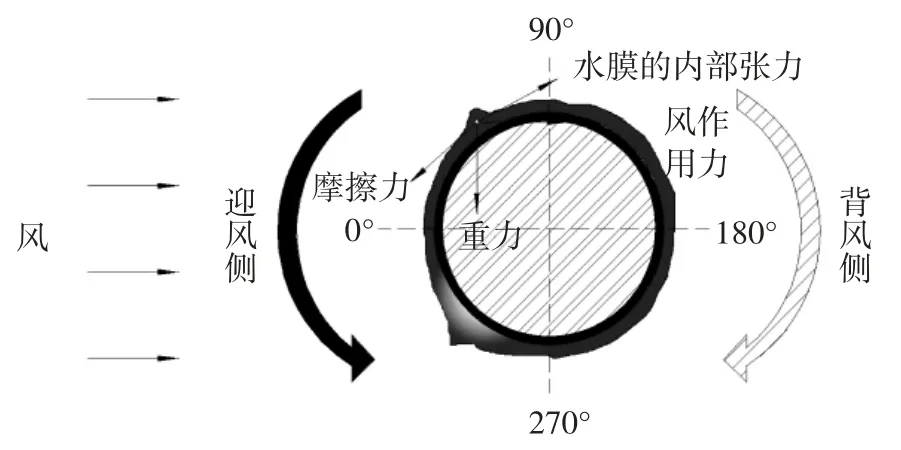
图14水膜受力及水线流动示意
图15 显示了气流正对棱边工况下正六边形拉索表面0~30 s的水膜形态变化时程.从图中可以看出下水线在θ=263°~299°之间发生周期性振荡并在θ=277°~288°之间出现了明显的积聚现象,积聚范围内水膜最大厚度约为1.2 mm,积聚位置水线宽度约为9.6 mm,整条下水线的宽度约为31.42 mm.下水线上边缘水膜厚度明显变薄说明水线流动情况与圆形拉索一样主要是从迎风侧由上水线流向下水线.图中有两条上水线形成,一条明显一条微弱,其中明显上水线的振荡范围是51°~63°,最大水膜厚度达到了1.15mm,水线宽度约为10.47 mm.在该条上水线下边缘处水线的周期性流动非常微弱,这是由于正六边形拉索的波浪形表面限制了上水线的流动和周期性脱落.微弱上水线的振荡范围是θ=102°~117°,最大水膜厚度约为0.42 mm,水线宽度约为13.1 mm.

图15工况一拉索表面水膜形态
图16 显示了气流正对索面工况下正六边形拉索表面0~30 s的水膜形态变化时程.从图中可以看出下水线在θ=233°~278°之间发生周期性振荡并在θ=268°~278°之间出现了明显的积聚现象,积聚范围内水膜最大厚度约为1.3 mm,积聚位置水线宽度约为8.73 mm,整条下水线的宽度为39.27 mm.水线流动情况与气流正对棱边工况类同.在θ=79°~135°范围内有多条宽度不一的上水线形成,水膜最大厚度约为1.13 mm.由于上水线条数较多且分布比较分散,这里不再具体一一列出其振荡范围和水线宽度.单条水线之间的共性是振荡范围和水膜宽度都较小,它们之间的周期性流动现象都很微弱.在气流方向和正六边形截面拉索的波浪形索面结构共同影响下,多条水线之间的流动受到了相互影响和制约从而阻碍了上水线的周期性环向振荡.
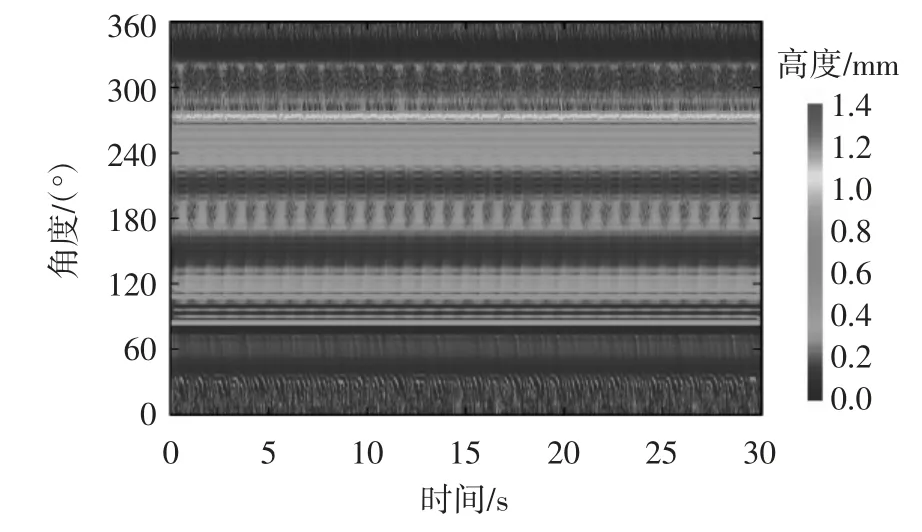
图16 工况二拉索表面水膜形态
3.4 上水线振荡区间内水膜厚度时程变化
3.4.1 圆形拉索
为深入分析圆形拉索表面上水线运动的周期特性,根据图13显示的圆形拉索表面上水线振荡范围31°~80°,考虑到拉索表面水膜厚度的计算结果是沿拉索环向离散点的数据,现选取上水线振荡范围内特征角度处的水膜厚度时程曲线进行分析.由于上水线并没有出现明显的积聚现象且水膜厚度变化范围不大,上水线振荡区间划分示意如图17所示,振荡区间上下边缘分别选取78.75°位置点和33.75°位置点,振荡区间中部位置选取59.06°位置点作为特征角度位置.共计抽取这三个特征角度位置进行0~30 s水膜厚度时程分析,如图18-20所示.
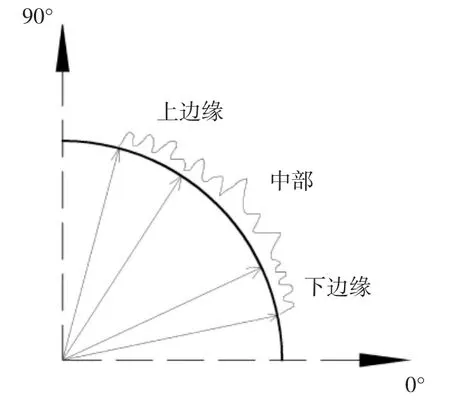
图17上水线振荡区间划分示意
图18 时程曲线显示:圆形拉索表面上水线振荡区间下边缘33.75°位置处的水膜厚度在前25 s内变化范围逐渐增大;25~30 s稳定下来并在0.093~0.4 mm范围内呈现出周期性变化,差值是0.307 mm.频谱分析显示,水线运动出现了明显的倍频和多主频振荡现象,主要振荡频率为0.998 Hz,能量幅值为0.032.文献[14]和[17]也曾多次提到倍频现象,这是因为上水线出现了回流现象而且回流这部分的水膜变化主频非常接近第一主频,然后累加得到的主频为第二主频且数值上约是第一主频的两倍[17].图19振荡区中部位置59.06°处的水膜厚度在前25 s内的变化范围仍然逐渐增大,25~30 s相对稳定并在0.187~0.39 mm范围内发生周期性变化,差值是0.203 mm,也呈现出多主频振荡现象,主要振荡频率为1.001 Hz,能量幅值为0.044.图20振荡区上边缘78.75°位置处水膜厚度在前25 s内呈现出增大趋势,25~30 s相对稳定并在0.194~0.267 mm范围内发生周期性变化,差值是0.073 mm.振荡主频为1.013 Hz,能量幅值大小为0.018.
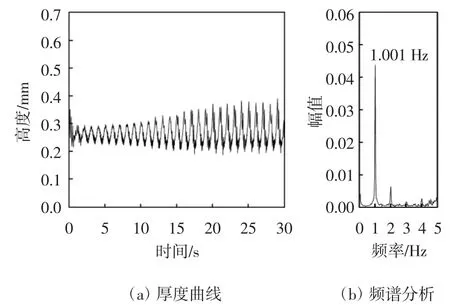
图19 圆形拉索振荡区间中部59.06°水膜厚度
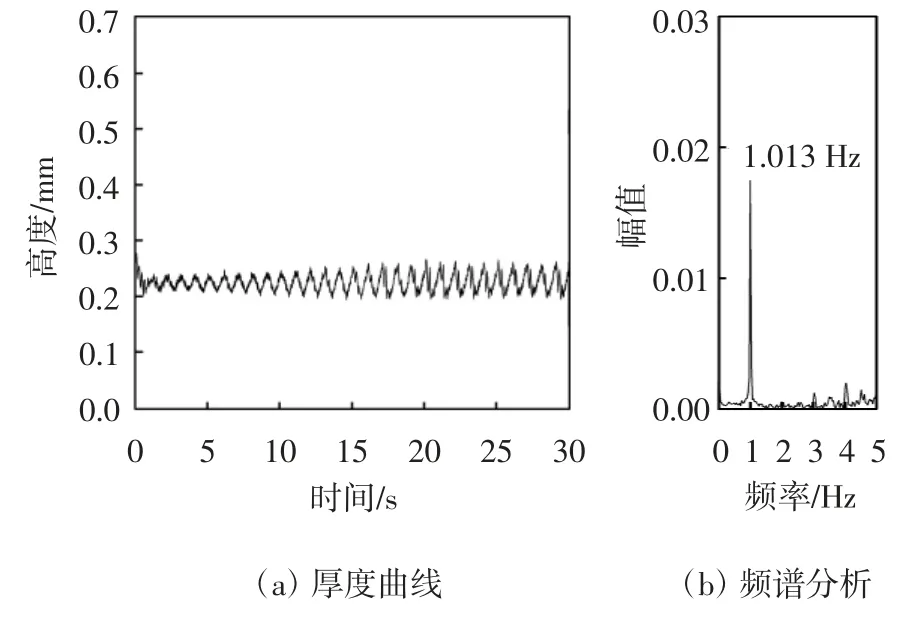
图20 圆形拉索振荡区间上边缘78.75°水膜厚度
振荡区间内水膜厚度的变化趋势与气动力、拉索振幅变化步调几乎一致,说明水膜厚度的改变引起气动力的改变进而引起拉索的大幅振荡.综合图18-20来看,振荡区间上下边缘及中部位置的振荡主频均接近拉索自振频率0.952 Hz,说明拉索和水膜之间的同频谐振是引起斜拉索风雨激振的主要原因[17].
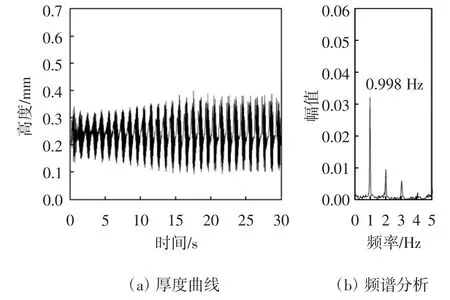
图18 圆形拉索振荡区间下边缘33.75°水膜厚度
3.4.2 气流正对棱边正六边形拉索
图15给出了气流正对棱边工况下正六边形拉索表面上水线振荡范围51°~63°,虽然110°附近位置处也有一条水线形成但是非常微弱,不用来做研究对象.考虑到拉索表面水膜厚度计算时得到的是沿拉索周边环向离散点的数据,为深入分析正六边形拉索表面上水线运动的周期特性,现选取上水线振荡区间内特征角度处的水膜厚度时程变化进行研究.振荡区间上下边缘分别选取63°位置点和51°位置点,振荡区间中部位置选取57°位置点作为特征角度位置.共计抽取这三个特征角度位置进行0~30 s水膜厚度时程变化及频谱分析,如图21-23所示.
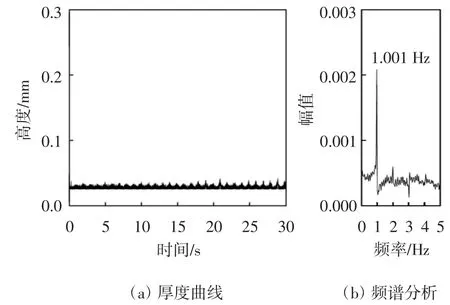
图21 工况一拉索振荡区间下边缘51°水膜厚度
从图21中可以看出,气流正对棱边工况下正六边形拉索表面上水线振荡区间下边缘51°位置处水膜厚度保持在0.025~0.043 mm范围内,差值为0.018 mm.水线振荡主频为1.001 Hz,能量幅值大小为0.002.图22振荡区间中部57°位置处水膜厚度在刚开始的0.5 s内发生不稳定的波动,然后0.5~30 s内水膜厚度在0.058~0.1 mm范围内发生周期性变化,差值为0.042 mm,水线振荡主频为1.001 Hz,能量幅值大小为0.007.图23振荡区间上边缘63°位置处水膜厚度在前0.2 s内发生不稳定波动,然后0.2~30 s内水膜厚度保持稳定,变化范围是0.025~0.038 mm,差值为0.013 mm.水线振荡主频是1.004 Hz,能量幅值大小为0.002.这三个特征角度位置水膜厚度非常薄,普遍在0.1 mm以下并且主频能量幅值都很低,导致了气动力变化的周期性大幅降低因此极大地减小了水线与拉索同频振动的可能性.
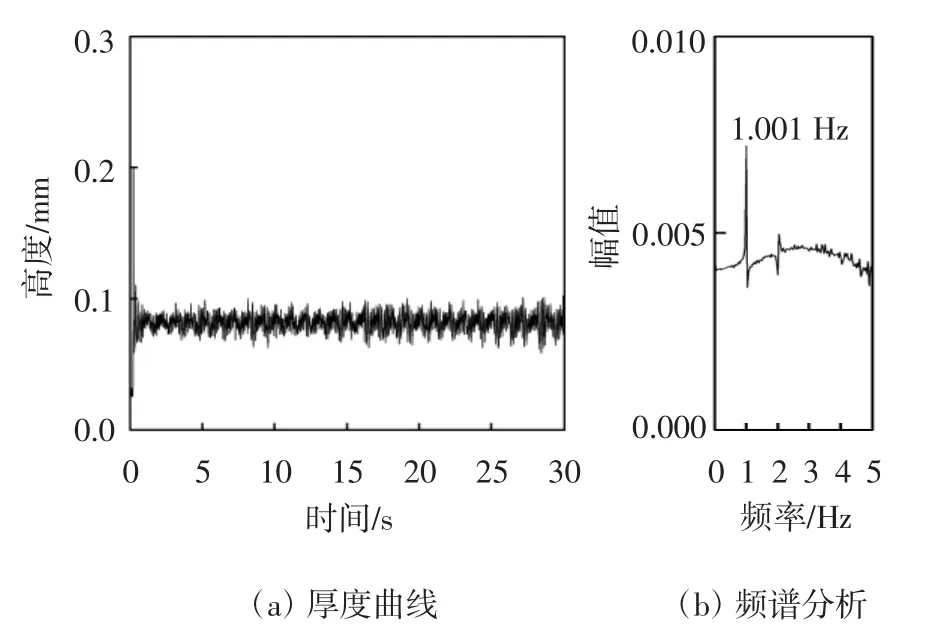
图22 工况一拉索振荡区间中部57°水膜厚度
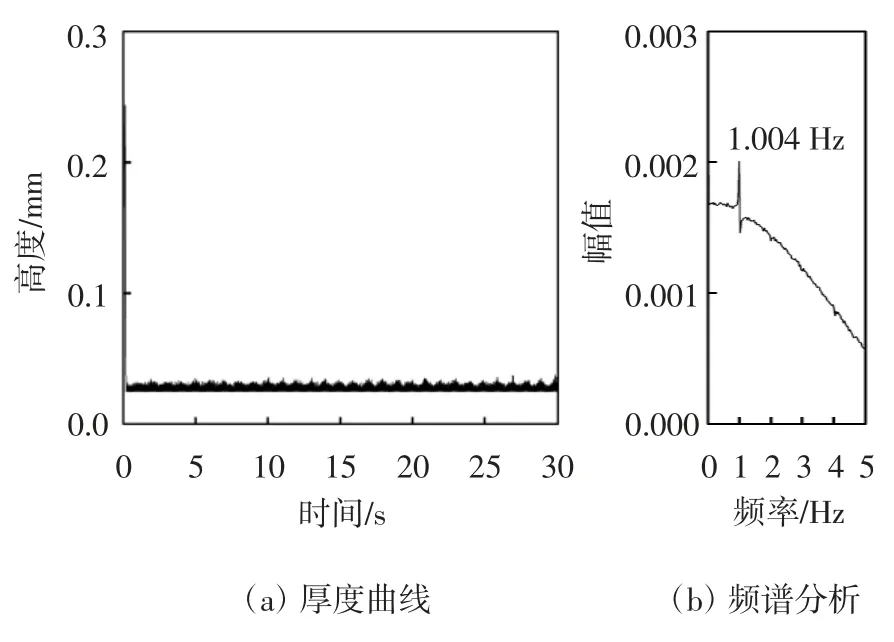
图23 工况一拉索振荡区间上边缘63°水膜厚度
3.4.3 气流正对索面正六边形拉索
从图16可以看出气流正对索面工况下正六边形拉索表面上水线振荡区间内有多条水线形成,振荡区间范围是θ=80°~133°,挑选θ=81°作为振荡区下边缘的特征角度;θ=108°作为振荡区中部位置的特征角度;θ=132°作为振荡区上边缘的特征角度.依次展开拉索表面上水线运动规律的深入分析,如图24-26所示.
从图24中可以看出,气流正对索面工况下正六边形拉索表面上水线振荡区间下边缘81°位置处水膜厚度在0.025~0.049 mm范围内变化,差值是0.024 mm.振荡主频是1.000 Hz,能量幅值大小为0.001 9.图25振荡区间中部108°位置处水膜厚度在前0.2 s内有些不稳定波动,然后0.2~30 s内水膜厚度保持稳定并在0.438~0.534 mm范围内呈现出周期性变化,差值是0.096 mm.振荡主频有两个分别是0.999,1.998 Hz,它们的能量幅值大小分别为0.014和0.012.图26振荡区间上边缘132°位置处水膜厚度在前0.3 s内发生波动,之后逐步稳定下来并在0.246~0.320 mm之间发生周期性变化,差值是0.074 mm.该位置处有两个变化主频分别是2.001 Hz和2.999 Hz,这两个主频的能量幅值分别是0.008 5和0.004.振荡区间中部位置和上边缘再一次出现了倍频现象.振荡区间下边缘和中部位置处的水膜厚度变化频率虽然很接近拉索自振频率,但是能量幅值很低,振荡区间上边缘水膜厚度变化主频已经远离拉索自振频率,导致气动力的周期性现象非常微弱,从而有效抑制了拉索的风雨激振现象.
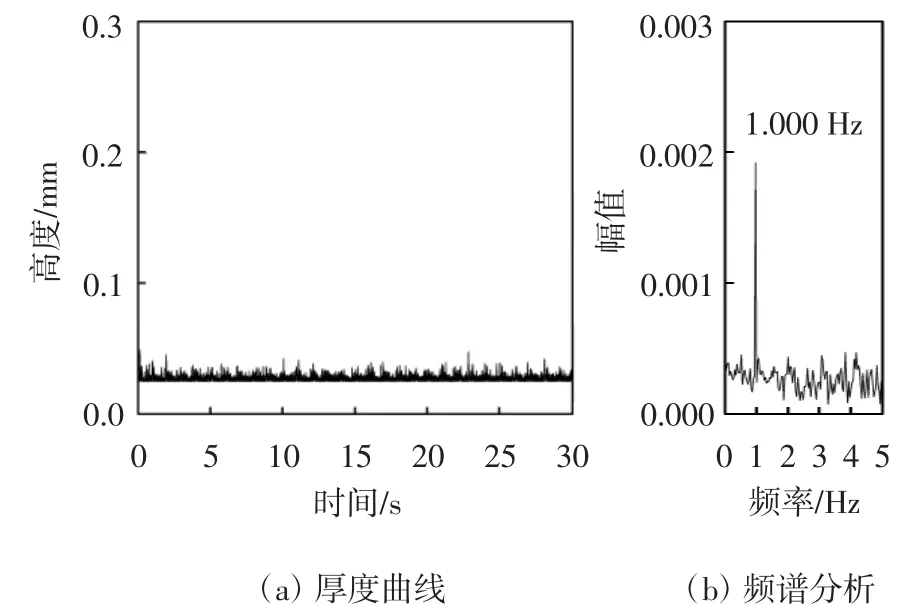
图24 工况二拉索振荡区间下边缘81°水膜厚度
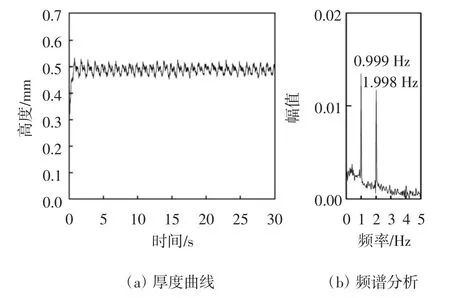
图25 工况二拉索振荡区间中部108°水膜厚度
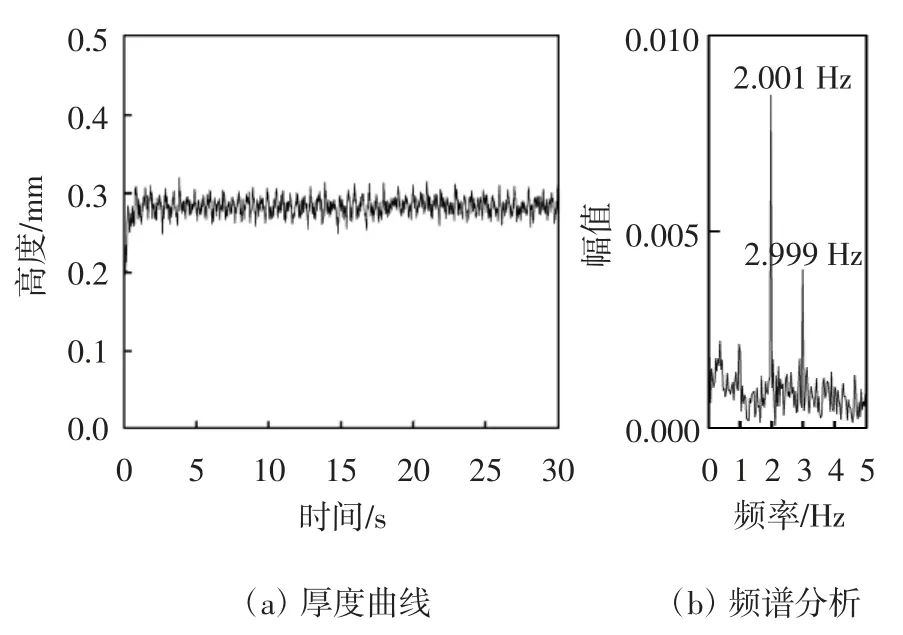
图26 工况二拉索振荡区间上边缘132°水膜厚度
4 结论
本文基于滑移理论,以正六边形斜拉索钝体绕流模型为研究对象,在COMSOL软件中计算随时间变化的风压力系数和风摩擦系数.然后在MATLAB软件中采用有限差分法求解拉索振动和水膜运动的偏微分方程,从拉索振动响应、气动升力、表面水膜形态变化、上水线振荡区间内水膜厚度时程变化以及上水线振荡规律这五个方面来深入分析正六边形拉索的抑振机理和减振效果,得出以下结论.
(1)在同等试验参数条件下,正六边形拉索相比圆形拉索,拉索振幅大为降低,具有良好的减振效果和工程应用价值.不同气流方向下正六边形拉索都具有良好的减振效果并且当气流正对索面时、即当风速方向与正六边形拉索索面垂直时减振效果最好.
(2)在不同气流方向工况下正六边形截面都减小了拉索气动升力的变化范围并且大大减弱了气动升力变化的周期性.当气流正对索面时、即当风速方向与索面垂直时气动升力周期性衰弱现象更加明显.
(3)正六边形拉索表面上水线振荡区间内的水膜厚度变化范围相比圆形拉索得到了显著的降低,水膜厚度变化主频出现了远离拉索自振主频的现象,主频能量幅值也得到了明显的减少,水膜厚度周期性变化得到了很大的衰弱.正六边形拉索虽然不能阻碍上水线的形成,但是它波浪起伏的外表面减小了上水线振荡区间范围,打乱了上水线的集中分布,明显抑制了上水线的周期性脱落和环向振荡.
(4)正六边形拉索的抑振机理是它波浪起伏的外表面抑制了上水线的周期性环向振荡,从而减弱了拉索表面气动力变化的周期性,进而有效抑制了拉索的风雨激振现象.

