基于视觉伺服的光束定向方法研究

◆彭城 杨洋 樊玉琦通讯作者

（1.合肥工业大学智能互联系统安徽省实验室 安徽 230601；2.中国科学院等离子体物理研究所 安徽 230031）

1 引言

在EAST 托克马克中采用了多种光学诊断技术来分析等离子体的可见光谱，例如电荷交换重组光谱（CXRS）[1]、滤镜[2]、运动斯塔克效应（MSE）[3]。其中MSE 诊断技术能够快速提供局部高精度的等离子体内部的磁场信号，结合等离子体平衡反演能获得可靠的电流密度分布。MSE 诊断系统在EAST 上的布局如图 1 所示，观察区集中在中性束注入装置（NBI）的中心轴上，观察区和NBI 中心轴都在EAST 的赤道面附近。观察区是一个窄条带，尺寸是855mm（长度）*50mm（宽度）。MSE 观察镜视野范围是18.48°，并划分为17个方向，以此来收集不同位置的等离子体辐射谱。

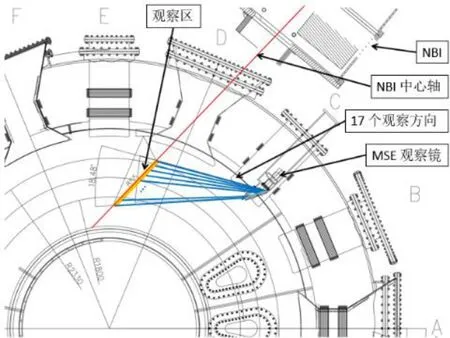
图1 EAST 托卡马克上的MSE 诊断系统布局图[4]

良好的光学诊断性能依赖于高精度的系统校准。传统校准方法是利用一个白板手动去捕捉光斑，在获取到光斑后，再使用激光测距仪或者高精度测量臂计算光斑的空间位姿。在整个测量过程中，需要手动移动白板，并需要在目视情况下，手动将测量臂末端的激光测距仪对准白板上的光斑中心，不仅费时费力，而且测量精度也难以保证。Huang 等人设计了一个高精度的四维标定转台，在水平轴向、俯仰、偏航和横滚四个维度利用高精度电机加上偏振光发生器产生已知空间方向的光束来校准MSE 诊断设备。该系统需要先手动控制水平轴向、俯仰和偏航三个维度的电机将偏振光发生器对准MSE 诊断设备，再控制横滚轴和偏振光发生器来校准MSE 诊断设备。此方法采用手动对准，所以效率不高[5]。Yang 等人提出了基于手眼系统的光束定向方法。在MSE 诊断设备处放置一个激光源，用机械臂携带一个专用的相机和投影白板装置，去截取激光束，在白板上生成投影点。然后用直线拟合算法计算出光束的方向，再将机械臂末端的偏振光发生器对准MSE 诊断设备[4]。该方法通过手眼系统将偏振光发生器对准MSE 诊断设备，提高了效率，减少了校准时间。

在本文中，整个光束定向方法主要参考了Yang 的设计，但采用更轻的固定架，以减少末端负载产生的误差，并且引入了视觉伺服功能来保证光斑的位置，较前期研究提升了精度和效率。事先给定的NBI 轴方向以及激光束大致方向可以保证相机获取到初始光斑位置，视觉伺服功能可以保证光斑在整个校准过程中始终处于白板的中心区域。工作人员仅需要控制机械臂靠近或远离激光源以获取不同位置的光斑即可。相比较传统的手动校准的方式，在精度和效率上有了极大的提升。最后通过搭建的物理实验装置得出，视觉伺服功能可以很好保证光斑的位置，光束定向的误差控制在0.32°以内，满足MSE系统光束定向所需要的精度。

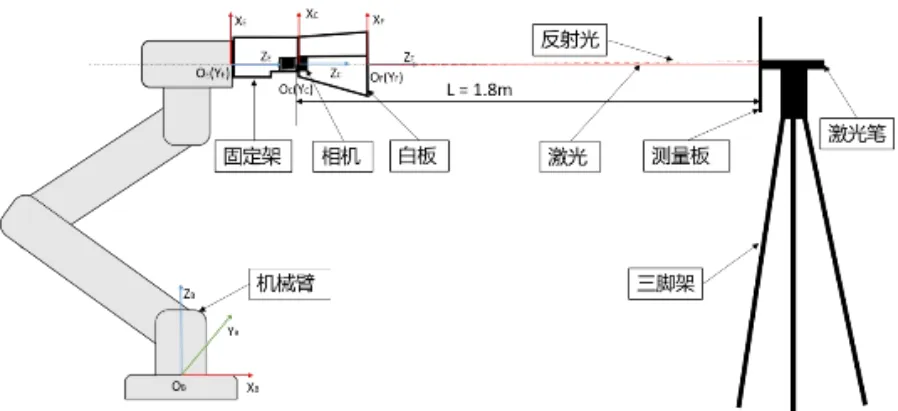
图2 光束定向方法原理示意图

2 基于视觉伺服的光束定向方法

本文提出了一种基于视觉伺服的光束定向方法，原理如下。机械臂末端携带一个铝合金固定架，固定架中间固定着一个相机，相机前方固定着一个半透明的平面玻璃白板。距离机械臂基座L 的地方，放置一个激光笔，以模仿MSE 诊断设备的激光源。激光打在白板上，相机就可以采集到光斑图片，对光斑图片进行处理获取光斑中心点坐标，再经过坐标变换得到光斑在机械臂基座坐标系下的空间坐标。为了实现坐标变换，需要对相机、白板位置以及手眼关系进行标定。最后通过直线拟合算法将多个光斑的空间坐标拟合，得到光束的空间方向。视觉伺服功能则保证在机械臂运动过程中，光斑始终投射在白板上。

2.1 光斑中心点坐标获取

首先将获取到的光斑彩色图转换为灰度图，如 (a)。由灰度图可以看出光斑的亮度明显高于其他区域，使用OpenCV 开源库的阈值二值化函数可以提取出光斑区域，如(b)。确定光斑区域后，再用轮廓提取函数提取出光斑的轮廓。考虑到激光大部分情况不是垂直照射白板的，形成的光斑多数是椭圆的，所以选择使用椭圆拟合算法来拟合提取到的轮廓。最后将拟合到的椭圆加到原图查看拟合效果，如(c)。可以发现拟合的椭圆可以很好的包裹着整个光斑。最后可以使用椭圆中心来代表光斑的中心点像素坐标md[ud,vd]T。

图3 获取光斑中心点像素坐标

2.2 坐标变换

空间点投影到图像上经历四个坐标系的变换：世界坐标系、相机坐标系、图像坐标系、像素坐标系，如所示。

世界坐标系是客观三维世界的绝对坐标系。相机和光束在三维空间中，需要在世界坐标系这个基准坐标系中来描述它们的位置，在本文中用机械臂基座坐标系（以下简称基坐标系）[XB,YB,ZB]T来表示。相机坐标系是以相机的光心为坐标原点，XC轴和YC轴分别平行于图像坐标系的X 轴和Y 轴，相机的光轴为ZC轴，用[XC,YC,ZC]T表示。图像坐标系是以CCD 图像平面的中心为坐标原点，X轴和Y轴分别平行于图像平面的两条垂直边，用[x,y]T表示。图像坐标系是用物理单位（mm）表示像素在图像中的位置。像素坐标系是以CCD 图像平面的左上角顶点为原点，u轴和v轴分别平行于图像坐标系的X 轴和Y 轴，用[u,v]T表示。像素坐标系是以像素为单位的坐标系。

图4 四坐标系关系图

像素坐标系与图像坐标系之间属于平面坐标变换，它们之间的转换关系为：

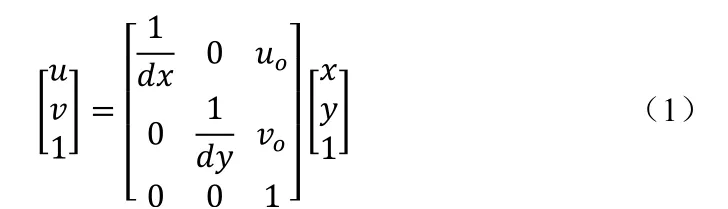
其中，[uo,vo]是图像坐标系原点在像素坐标系中的坐标，dx和dy分别是每个像素在图像平面X 轴和Y 轴方向上的物理尺寸。

在针孔相机模型中，图像坐标系与相机坐标系之间是相似三角形变换，公式为：

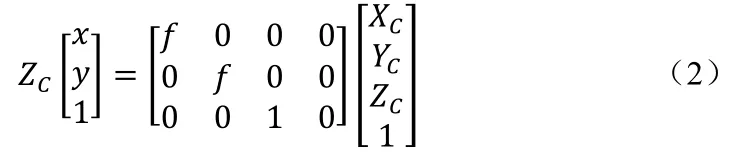
其中f为焦距（图像平面与相机坐标系原点的距离）。故像素坐标系到相机坐标系之间的变换可以写成：

为相机的内参，用K表示。

相机坐标系与基坐标系的变换为空间坐标变换，公式为：

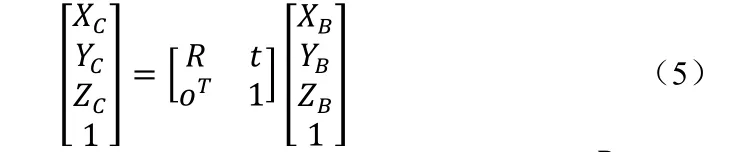
其中，R为3×3正交旋转矩阵，t为三维平移向量。也叫相机的外参，可以用表示，联立公式-得：

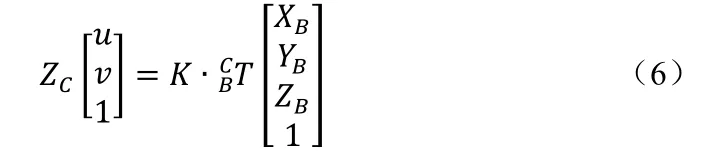
在上面的公式推导过程中，我们采用了针孔相机模型来描述物和像之间的相似三角形的关系。但实际上相机镜头在加工和装配过程中会存在误差，导致相机图像平面上实际所成的像与理想成像之间存在畸变。带畸变的相机成像模型如所示。

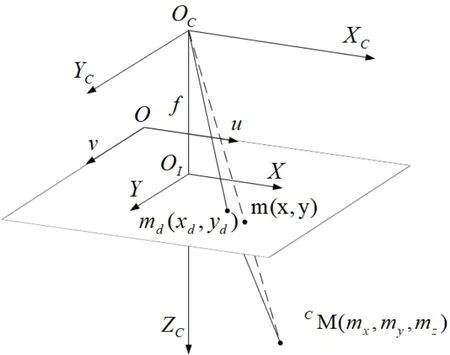
图5 相机畸变模型

其中，md[xd,yd]表示实际投影点的图像坐标系下的坐标，带有畸变，m[x,y]表示理想投影点的图像坐标系下的坐标。镜头畸变模型可表示为：

σx和σy是非线性畸变值，它包括径向畸变和切向畸变等。畸变模型可由公式-来表示：

联立公式-可得：

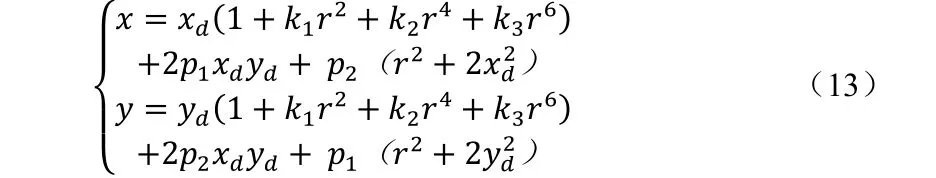
其中，k1,k2,k3表示径向畸变系数，p1,p2表示切向畸变系数，r=

至此，已建立从像素坐标系到基坐标系的坐标变换关系。通过相机的畸变系数σ[k1,k2,k3,p1,p2]对光斑中心点的坐标进行矫正，通过相机的内参K和外参，就可以根据公式求出光斑中心点在基坐标系下的空间坐标。

2.2.1 相机标定

相机的畸变系数σ[k1,k2,k3,p1,p2]和内参K是相机的固有参数，对相机进行标定就可以获取到这些参数。本文采用了使用最广泛的张正友0相机参数标定算法。

准备一个12*9 的黑白棋盘格，固定相机不动，在保证棋盘格一直在相机视野的前提下，采集不同位姿下的棋盘格图片。采集完成后，对相机进行校准。校准结果如下：

2.2.2 白板位置标定

白板固定在相机正前方，使得相机可以看到白板有效区域。白板坐标系以[XF,YF,ZF]T表示，坐标系原点在白板中心。将标定板放在白板上，如所示，标定板和白板之间的坐标变换是一个平移变换。因此，在求解出标定板相对于相机的坐标变换之后，再加上一个平移变换，就可以得出白板相对于相机的坐标变换。

图6 白板位置标定

求解相机和标定板之间的坐标变换是一个典型的PnP 问题，本文采用DLT 算法来求解该坐标变换。棋盘格标定板的每个方格边长是已知的，假设标定板在XGOGYG平面上，对每张拍摄的棋盘格图片，可以通过角点检测算法获得图片中棋盘格的所有角点。设角点Q 在标定板坐标系下齐次坐标GQ=[qx,qy,qz,1]，其在像素平面上对应的投影特征点。相机与标定板之间的坐标变换为：

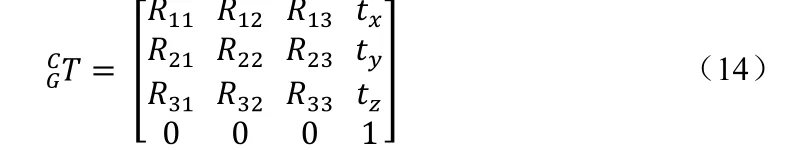
由0 节坐标变换可知：

用式第三行把ZC/K 消去，得到两个约束：

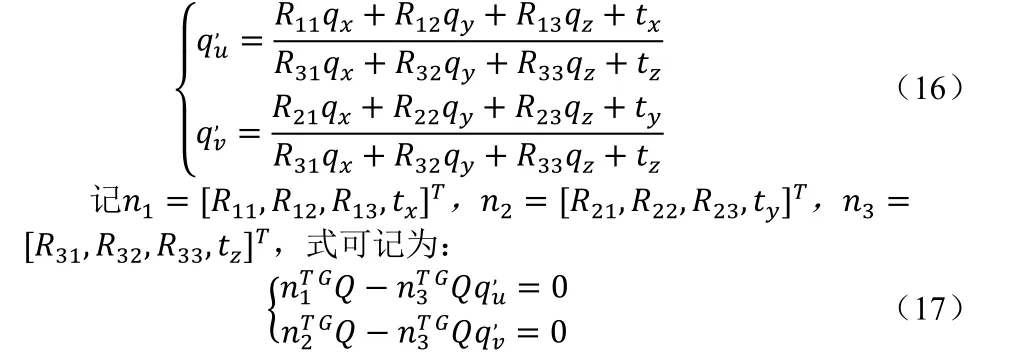
每个特征点提供了关于n（n1,n2,n3）的两个线性约束，对于有12 个未知数的，6 对匹配点即可求得。此时标定板的原点在相机坐标系下的坐标为COG=[tx,ty,tz]。重复多次，即可用多个棋盘格的原点坐标拟合出棋盘格所在的平面。用拟合出来的平面数据更新。用游标卡尺测得标定板的厚度为h=1.07mm，即可得到白板相对于相机的坐标变换矩阵：

2.2.3机械臂手眼标定

一个棋盘格被放置在场景中，并且棋盘格相对于机械臂基座位置不变，这意味着基坐标系与棋盘格的关系是固定不变的。移动机械臂末端，并保证相机始终能够看到整个棋盘格，可以得到公式和。

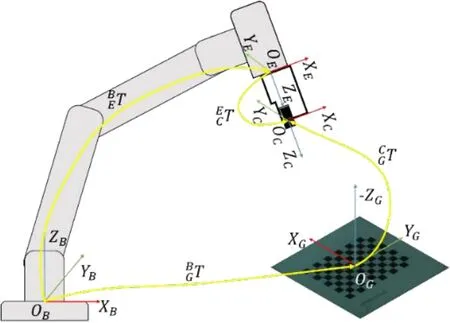
图7 手眼系统标定坐标系关系图

2.3 激光光束定向

由可知，相机坐标系下任意一点CM[mx,my,mz]的投影射线经过原点OC[0,0,0]和点m[x,y]。点m在相机坐标系下的坐标Cm[x,y,f]。为了得到x和y，需要对之前获取到的光斑中心点md[ud,vd]T用公式做畸变校正。本文使用OpenCV 中的undistortPoints（）函数来完成该校正。设从相机光学中心到空间点M的投影射线的方向向量为。则

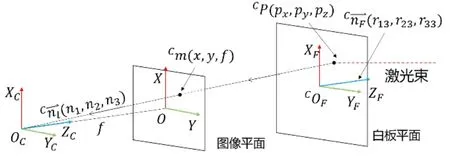
图8 线面交点

点CP 在投影射线上，故有：

同时点CP 在白板平面上，则有：

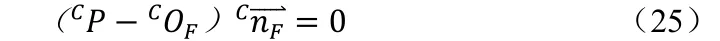
联立公式和，消去CP，得：

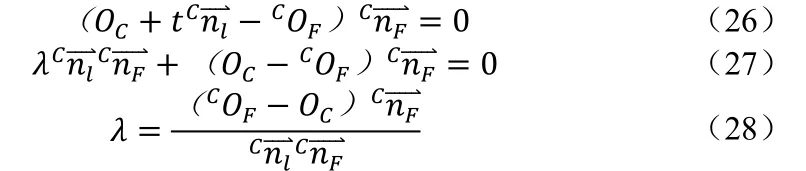
联立公式和即可算出激光点CP 的坐标。并且通过公式即可计算出在基坐标系下的激光点坐标BP′。

其中i代表激光点的数量。

移动机械臂到新的位置，获取新的激光点，并执行与本节所描述的相同的计算过程，以获得新的激光点位置。当i＞2 时，可以用最小二乘法来拟合光束的空间方向。

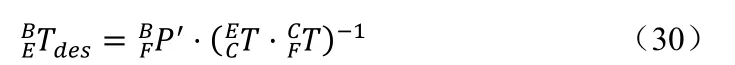
最后，采用雅克比逆运动学求解器计算要发送给机械臂运动控制器的有效关节值。

2.4 视觉伺服

视觉伺服利用视觉信息对机器人或者相机位姿进行伺服控制,其目标是控制机器人或者相机逐步到达期望的位姿。视觉伺服按照控制系统的构成方式分为基于位置的视觉伺服（PBVS）控制、基于图像的视觉伺服（IBVS）控制0。IBVS 相对于PBVS 来说，具有较少的计算量，当存在图像量化误差、摄像机标定误差和图像噪声时，IBVS 可以更好地定位与跟踪。

本文的视觉伺服控制采用IBVS 方法，目的是最小化图像误差，该误差可以定义为：

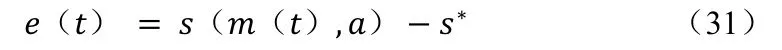
其中，m（t）通常是特征点在图像上的像素坐标，a通常是相机的内参。将提取的特征m（t）映射至目标特征s*的空间中，并与s*进行比较。当e（t）为零时，系统达到稳定的收敛位置0。

因为希望保持光斑点始终在图像中心区域，所以s为光斑中心在图像坐标系下的坐标，而s*为图像中心的坐标。

两边求导可得：

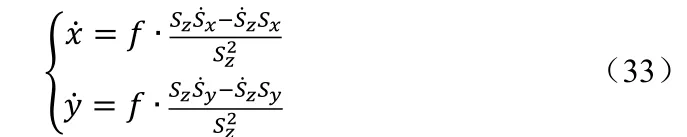
根据刚体运动学，有：

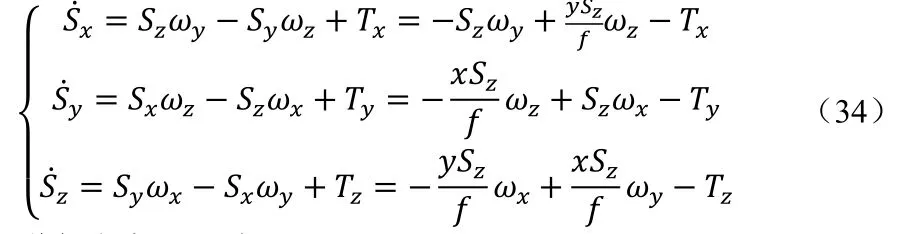
联立公式,,，可得：

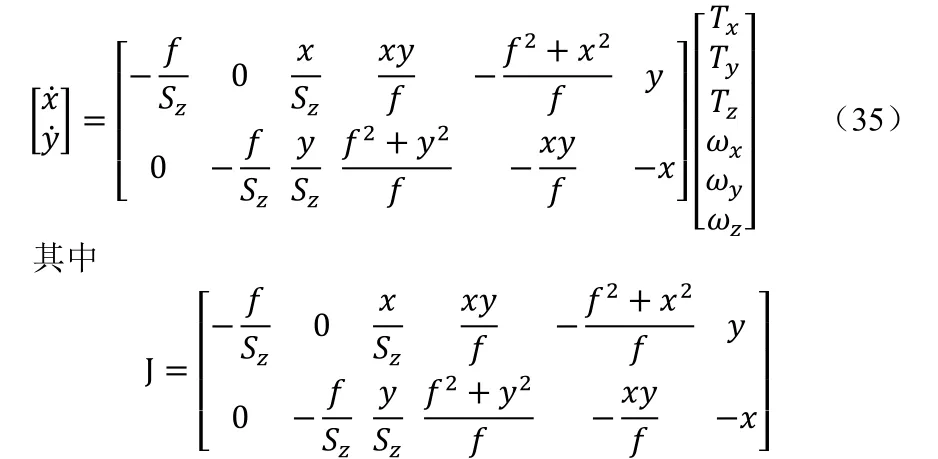
为图像雅克比矩阵0，也称交互矩阵。通过交互矩阵可以建立图像变化与机械臂末端运动之间的关系。由上式可知，至少需要三组特征点s 的变化率才能求解得到对应的相机速度CV，再根据坐标变换矩阵即可算出机械臂末端的速度。本文仅需考虑将光斑控制在白板中心即可，因此只需要控制机械臂末端X、Y轴平移就可实现所需要求。等式可以简化为：

图10 光束定向方法验证平台

3 实验

3.1 光束定向方法验证平台硬件设计

验证平台包含硬件部分和软件控制部分。硬件部分由新松(GCR5)6 自由度机械臂、铝合金固定架、半透明玻璃白板、Basler(acA1920-48gc)相机以及Computar M0814-MP2 镜头组成，如图9 所示。新松6 自由度机械臂末端固定着一个铝合金材质的固定架，来尽可能降低整个相机模块的重量来减少机械臂的负载，以减少重力误差。上方固定着旋转偏振光发生器用于后续MSE 系统测试。下方固定着相机，相机前方固定着一块白板，白板的有效面积为100×100mm，由玻璃制作，一面粘贴半透明纸，入射激光束可由正面反射。激光打在半透明的白板上，相机采集图片，对图像处理即可获取光斑的中心点像素坐标。通过坐标变换即可获取到光斑的空间坐标。最后通过直线拟合就可以计算出光束方向。在计算出光束方向后，将白板的法向量与光束方向对齐，半透明的白板就会将光束反射回去。根据光反射原理，激光应该被反射到发射点。距离机械臂基座L=1.8m 处（MSE 观察镜到观察区域平均距离）放置一个激光源，将极坐标纸贴在激光笔上，白板将激光反射打在测量板上，测量激光源中心与反射激光点中心之间的距离D，激光束对准精度可描述为：

其中，θ表示激光束入射光线向量与反射光线向量之间的夹角。

3.2 光束定向方法验证平台软件设计

在硬件平台基础上基于RobWorkStudio0仿真软件，采用Visual Studio 和Qt 混合编程开发了光束定向方法验证平台软件，以完成图像的采集、光斑中心提取、坐标变换、直线拟合、机械臂控制等功能。

是软件操作界面，包括机械臂状态区、相机控制区、机械臂控制区、操作按钮区、以及日志等区域。红色框选的是相机控制区，包含几个相机常用控制按钮，并且可以实时看到相机采集的图像。蓝色框选的是机械臂控制区，可以手动控制机械臂移动。左边是机械臂状态区可以看到机械臂当前的工作状态。绿色框选的是操作按钮区，包括视觉伺服开启关闭、仿真现实切换、图像采集、图像加载、图像存储、空间方向拟合、方向对齐等功能。最下面则是日志输出。

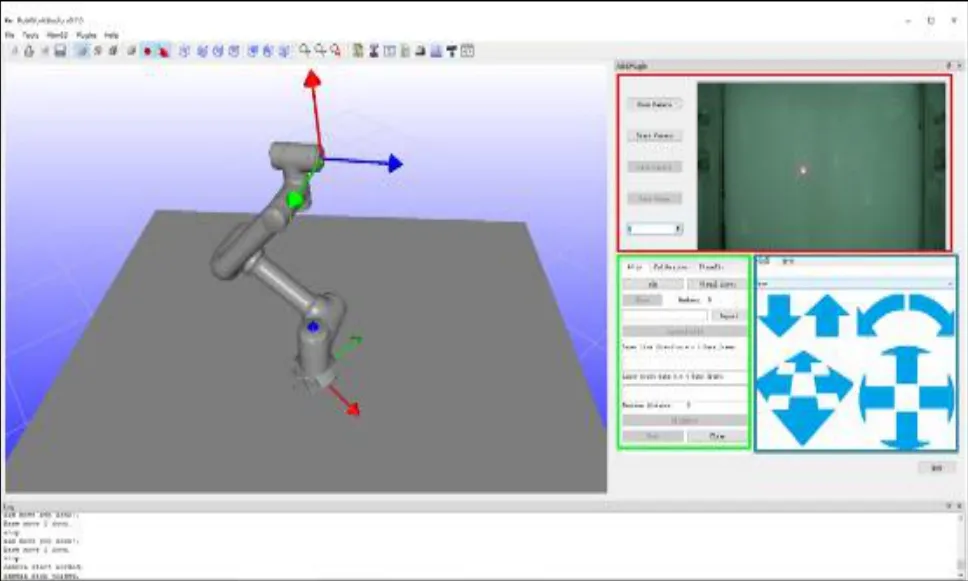
图11 软件界面图

3.3 光束定向方法验证

是工作流程图，工作流程如下：软件启动后加载机械臂模型。检查机械臂和相机等硬件的连接状态和初始的NBI 轴方向、激光束大致方向参数是否准确。若机械臂和相机都在线，即可在线实时的光束定向。开启相机，与真实机械臂建立通信，这时候相机采集的图片将实时显示在相机控制区，机械臂状态也将与真实机械臂保持同步。打开视觉伺服功能后，机械臂将会自动运动来保持光斑点在相机视野中心区域。点击shoot 按钮便采集了第一张图片，经过0 节获取光斑中心点坐标后，若满足要求，则记录下光斑的坐标以及机械臂的位姿数据。然后手动移动机械臂到达新的位置，再采集新的图片。当满足要求的光斑的数据达到指定的数量后，便可以进行直线拟合计算出光束的空间方向。

最后再移动机械臂使得白板法向量与光束方向重合，获得测量板上反射点和光源之间的距离D，以及方位角。

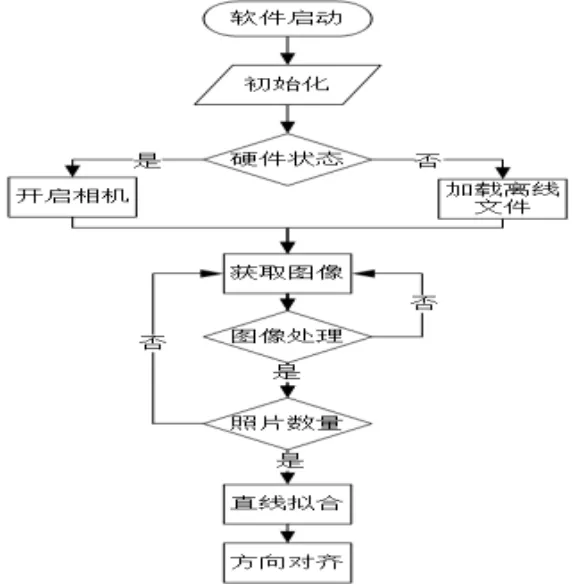
图12 光束定向方法工作流程图

3.4 结果分析

实验分成三组，第一组取3 个光斑点来拟合直线，第二组取5个，第三组取7 个，每组重复24 次，记录下反射点的极坐标，如所示。每组最大、最小和平均偏离距离D以及根据公式计算出对应的偏离角如所示。计算每组数据的协方差矩阵和协方差的特征值、特征向量，由于协方差的最大特征向量总是指向数据方差最大的方向，且特征向量对应的特征值为数据在特征向量方向上的方差，因此使用最大特征值来描述数据的离散程度。计算结果如所示。根据上述计算结果，画出95%置信椭圆。如 中3、5、7 点拟合结果图左上角所示。

由可知，该方法平均误差控制在0.3°以内，最大误差为0.32°低于0.5°，满足MSE 系统的光束定向要求。由可知，随着拟合的点数增加，最大特征值在降低，说明反射点越来越集中，拟合效果越好。5 点时最大特征值最小，拟合最好。

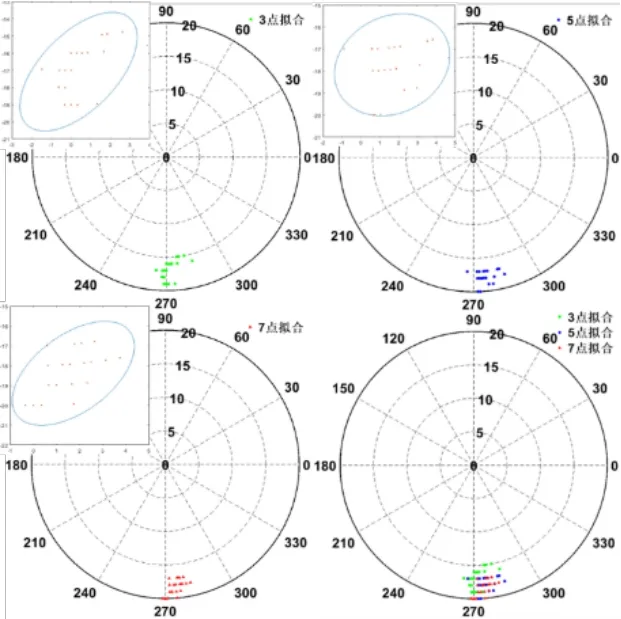
图13 3 点拟合结果（左上）、5 点拟合结果（右上）、7 点拟合结果（左下）、全部拟合结果（右下）

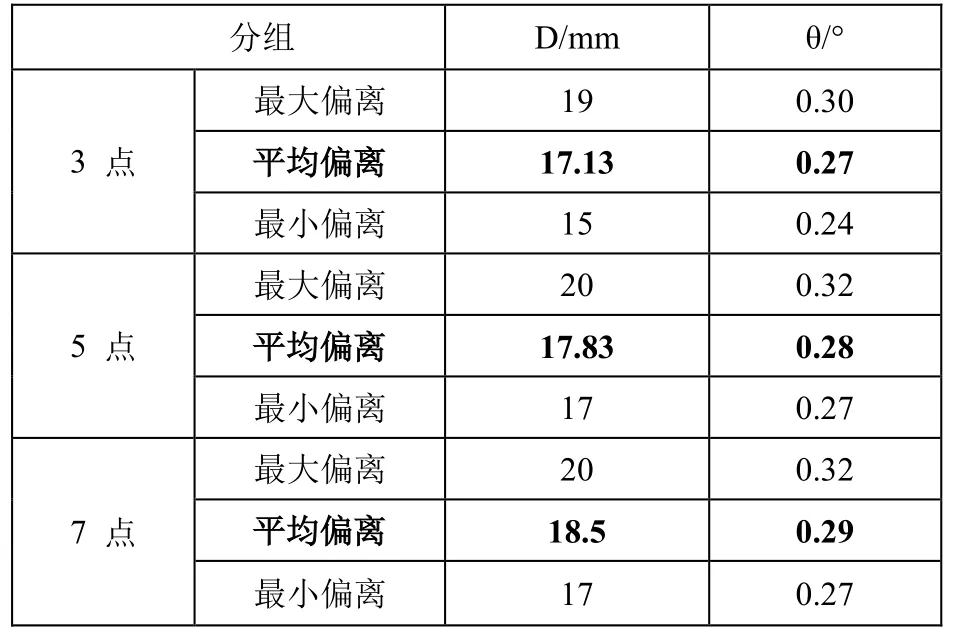
表1 拟合结果

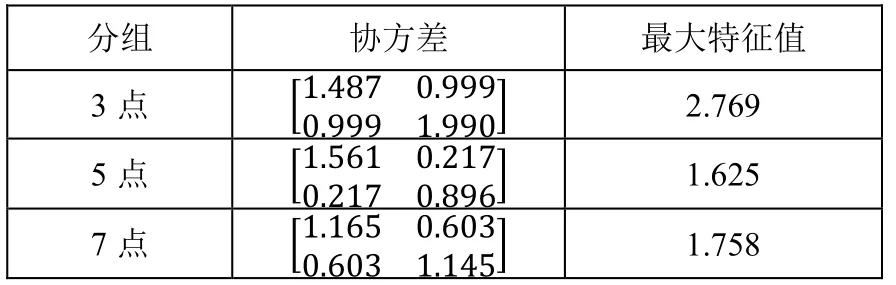
表2 协方差结果

综上，实验表明，该方法可以很好的测量出光束的空间方向，平均误差在0.28°，完全可以满足MSE 测试的需要，且重复性测试结果均分布在较小范围内，说明该方法精度高，稳定性好。