基于MILP寻找SM4算法的差分特征

潘印雪 王高丽 倪建强

1(上海市高可信计算重点实验室(华东师范大学) 上海 200062) 2(密码科学技术国家重点实验室 北京 100878)

对称密码(symmetric cipher)算法作为保障数据安全的基础，其自身的安全性至关重要.一个对称密码算法从设计问世到被广泛使用，要经过严格的安全性评估.安全的对称密码算法要能够抵抗现有的分析方法，如：差分分析[1]、线性分析[2]、积分分析[3]、立方攻击[4]等.分组密码(block cipher)是对称密码的重要组成部分，其设计主要采用3种结构：Feistel结构、SPN结构以及Lai-Massey结构.其中,采用Feistel结构的典型算法包括DES[5]，SM4[6]算法等；采用SPN结构的典型算法包括AES[7]，SKINNY[8]算法等；采用Lai-Massey结构的算法包括IDEA[9]，FOX算法[10]等.

在评估分组密码的安全性时，密码的非随机性质可用来区分密码算法和随机置换，分组密码中最重要的分析工具之一是差分分析[1].差分分析是由Biham和Shamir提出，最早将其应用于DES的分析，之后差分分析被应用在更多对称密码算法上，并且逐步衍生出许多的变体，知名的变体方法有截断差分[11]、不可能差分[12]、高阶差分[13]、飞去来器攻击[14]和差分线性攻击[15]等.差分分析通过研究特定的明文差分在加密过程中的概率传播特性，将分组密码与随机置换区分开，并在此基础上进行密钥恢复攻击.差分分析的第一步也是最重要的一步，是寻找高概率的差分特征，最经典的方法是Matsui分支定界深度优先搜索算法[16].近年来，基于求解器的自动化搜索技术[17-24]在寻找密码算法的区分器时发挥了越来越重要的作用，其中基于混合整数线性规划(mixed integer linear programming, MILP)[17-19]的自动化搜索技术被广泛用于搜索差分特征.

SM4(SMS4)算法[6]发布于2006年，于2012年成为国家密码行业标准(GM/T0002—2012)，于2016年成为国家标准(GB/T32907—2016).自问世以来，SM4算法一直广受海内外学者的关注和研究[22,25-32].2008年，Zhang等人[25]给出5轮SM4算法的迭代差分特征，并给出了16轮SM4算法的矩形分析和21轮SM4算法的差分分析.同年，Kim等人[26]给出了22轮SM4算法的线性分析和差分分析，其中，线性分析的时间复杂度为2117个已知明文，时间复杂度为2109.86次加密运算，差分分析的数据复杂度为2118个选择明文，时间复杂度为2125.71次加密运算.2009年，Su等人[27]给出了19轮SM4算法的差分特征，并给出了23轮SM4算法的分析，数据复杂度为2115个选择明文，时间复杂度为2124.3次加密运算.2009年，Zhang等人[28]也给出了23轮SM4算法的差分分析，数据复杂度为2127个选择明文，时间复杂度为2121.7次加密运算.

近年来，密码学家将基于求解器的自动化搜索技术用于分析SM4算法.2016年，张建等人[31]通过研究SM4算法多轮之间的关系，基于MILP建模评估了缩减轮SM4算法的活跃S盒下界.2019年，Wu等人[32]基于MILP建模重新评估了缩减轮SM4算法活跃S盒下界，并找到了8条19轮SM4算法概率为2-124的差分特征.2021年，Liu等人[22]基于简单定理证明器(simple theorem prover, STP)建模给出了19轮SM4算法概率为2-123的差分特征.

Mouha等人[33]提出字节级MILP模型，该模型实现了异或运算、线性变换以及S盒运算的建模，并用该模型给出了AES最小活跃S盒的个数，但该模型无法刻画S盒的差分传播特性.在Asiacrypt 2014大会上，Sun等人[34-35]扩展了Mouha的模型，并提出比特级MILP框架.该框架介绍了如何对S盒的差分传播特性建模，并用贪心算法删减了刻画S盒的线性不等式中的冗余.然而当S盒状态增大时，刻画S盒的线性不等式中会包含大量的冗余，即使是运用贪心算法删减掉部分的冗余，仍然可能导致寻找差分特征的效率太低.Sasaki和Todo[36]针对S盒差分传播特性的建模提出了新的解决方案，即对于刻画S盒的线性不等式，该方案基于MILP建模来删减其中的冗余，从而可以得到指定数量的线性不等式.同时文献[36]也发现当刻画S盒的线性不等式数量最少时，搜索差分特征的效率不一定最高.相对于采用8-bit的S盒的密码算法，文献[33-36]所提的建模方法寻找差分特征的效率太低，以致于程序运行了很长时间都得不到结果.

Abdelkhalek和Sasaki等人[37]提出针对8-bit的大状态S盒的建模方法，并用此模型评估了SKINNY-128的安全性.该模型对于S盒的建模没有基于凸包的H-representation原理，而是将逻辑条件建模转化为最小化布尔函数的和乘积问题，软件Logic Friday可以自动解决转化问题.在这种情况下S盒建模后的线性不等式系数均为0,1和-1.对于采用8-bit S盒的AES算法，该模型刻画S盒的不等式个数超过8 000.2019年，Wu等人[32]重点关注状态大于6-bit的S盒建模问题，基于凸包的H-representation原理观察S盒线性不等式系数与其排除的不可能差分模式之间的关系，提出一种从小状态S盒建模推导大状态S盒建模的方法.对于AES算法的S盒，文献[33]生成的刻画S盒的不等式个数小于4 000.值得注意的是，无论是采用8 000个线性不等式还是采用4 000个线性不等式，当密码算法的轮数增多时，自动化建模寻找差分特征的计算量都很大.

本文的主要贡献包括2个方面:

1)重新评估了1～24轮SM4算法的活跃S盒个数的下界，对于19轮SM4算法，当活跃S盒个数为19时，给出了概率为2-123的差分特征，这是目前基于MILP建模找到的SM4算法轮数最多、概率最大的差分特征.文献[22]基于STP建模找到了19轮SM4概率为2-123的差分特征，本文的差分特征与文献[22]的差分特征不同.

2)受文献[32,37]的启发，本文采用基于凸包的H-representation原理、布尔函数和乘积原理相结合的方式刻画8-bit的S盒差分传播概率特性，改进了搜索基于大状态S盒密码算法差分特征的模型.

1 SM4算法介绍

分组密码算法SM4采用非平衡的广义Feistel结构，其迭代轮数为32，分组状态和密钥状态均为128 b.第i轮加密运算如图1所示，其中Xi和RKi的长度均为32 b.

(X0,X1,X2,X3)和(Y0,Y1,Y2,Y3)分别表示128-bit的明文P和密文C,RKi代表轮密钥，加密过程为：

对于i=0,1,…,31，

Xi+4=F(Xi,Xi+1,Xi+2,Xi+3,RKi)=

Xi⊕T(Xi+1⊕Xi+2⊕Xi+3⊕RKi),

其中F(·)表示轮函数.

在最后一轮的后面进行R变换：

(Y0,Y1,Y2,Y3)=R(X32,X33,X34,X35)=

(X35,X34,X33,X32).

SM4算法第i轮的变换为

(Xi,Xi+1,Xi+2,Xi+3)→(Xi+1,Xi+2,Xi+3,Xi+4),

其中Xi+4=Xi⊕T(Xi+1⊕Xi+2⊕Xi+3⊕RKi),T函数是由非线性操作S盒和线性变换L组成.S盒采用4个相同的8×8的S盒，S盒的差分分布表(differential distribution table, DDT)概况如表1所示：

Table 1 Overview of S-box DDT of SM4 Algorithm

线性变换L由循环移位和异或操作组成，即

L(S)=S⊕(S<<<2)⊕(S<<<10)⊕

(S<<<18)⊕(S<<<24),

文献[32]给出了SM4算法差分特征在多轮之间传播的性质，其中用到的符号如下.

(ΔXi,ΔXi+1,ΔXi+2,ΔXi+3)表示第i轮的输入差分，记ΔXi=(Δx4i+1,Δx4i+2,Δx4i+3,Δx4i+4).T函数的输入差分记为ΔIni=(Δz4i+1,Δz4i+2,Δz4i+3,Δz4i+4)，输出差分记为ΔOuti=(Δw4i+1,Δw4i+2,Δw4i+3,Δw4i+4).另外，记

ΔFi=ΔXi+1⊕ΔXi+3，

ΔYi=ΔXi+2⊕ΔXi+3，

ΔFi=(Δf4i+1,Δf4i+2,Δf4i+3,Δf4i+4)，

ΔYi=(Δy4i+1,Δy4i+2,Δy4i+3,Δy4i+4)，

那么有

ΔIni=ΔYi-1⊕ΔXi+3，

ΔIni=ΔXi+1⊕ΔYi，

ΔIni=ΔFi⊕ΔXi+2.

性质1[31].对于任意连续3轮的SM4算法，有Δf4i+k=Δf4i+8+k⟺Δw4i+4+k=0，其中i∈{0,1,…,31},k∈{1,2,3,4}.

性质2[31].对于任意连续3轮的SM4算法，由等式Δx4i+4+k=Δx4i+16+k,Δw4i+4+k=0,Δy4i+8+k=0中的任意2个等式都能推导出剩下的一个等式.

性质3[31].对于任意连续3轮的SM4算法，由等式Δx4i+8+k=Δx4i+20+k,Δw4i+4+k=0,Δy4i-4+k=0中任意2个等式都能推导出剩下的一个等式.

性质4[31].如果SM4算法的输入差分不为零，那么对任意连续4轮，至少存在一个活跃S盒.

性质5[31].对于连续5轮的SM4算法，下式成立：

ΔIni⊕ΔIni+4=ΔOuti+1⊕ΔOuti+2⊕ΔOuti+3.

性质6[31].对于连续5轮的SM4算法，如果Δx4i+8+k=Δw4i+12+k，那么有Δx4i+8+k=Δw4i+12+k.

性质7[31].对于连续6轮的SM4算法，如果Δz4i+k=Δz4i+4+k=Δw4i+4+k=0，那么有Δz4i+16+k⊕Δw4i+16+k=Δz4i+20+k.

性质8[31].对于任意连续6轮的SM4算法，如果Δz4i+16+k=Δz4i+20+k=Δw4i+16+k=0，那么有Δz4i+4+k⊕Δw4i+4+k=Δz4i+k.

性质9[31].对于任意连续6轮的SM4算法，如果ΔIni⊕ΔIni+1⊕ΔIni+4⊕ΔIni+5≠0，则可以得到wt(ΔSIni+1⊕ΔSIni+4)+wt(ΔIni⊕ΔIni+1⊕ΔIni+4⊕ΔIni+5)≥5.

2 基于大状态S盒密码算法的MILP模型

2.1 字节级MILP模型

评估密码算法抵抗差分分析安全性的一个实际指标是确定活跃S盒数量的下界.2011年，Mouha等人[33]基于MILP建模来自动化寻找密码算法最小活跃S盒的个数.

对于分组密码中基于字节的操作，文献[33]引入0，1变量表示字节差分，1代表字节差分非0，0代表字节差分为0.

对于异或操作建模过程为：设a,b,c是异或操作的输入和输出差分，即a⊕b=c.根据异或的性质：如果输入差分为0，那么输出差分为0；如果输入差分和输出差分不全为0，那么a,b,c这3个变量至少有2个变量非0.以下约束可保证：1)a,b,c全部为0;2)a,b,c不全为0，则其中至少有2个非0：

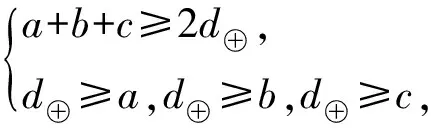
其中虚拟变量d⊕∈{0,1}.

对于线性转换建模过程为：设M=(m0m1…mμ-1)和N=(n0n1…nμ-1)分别表示线性转换L的字节级输入差分和输出差分，其中mi,ni∈{0,1}，则有约束关系：

其中,BL为线性转换L的分支数.

对于S盒操作，字节级模型不需要额外的约束，需注意的是目标函数为全轮S盒字节级输入差分的目标函数为求解最小值，这样可得到活跃S盒个数的下界.目标函数为

Minimize:∑∑mi.

2.2 比特级MILP模型

2014年，Sun等人[34-35]扩展了Mouha等人[33]的字节级MILP框架，提出比特级MILP模型，该模型可以搜索密码算法最小活跃S盒个数和具体的差分特征.考虑到搜索差分特征的效率，该模型主要适用于采用4-bit的S盒的密码算法.另外Abdelkhalek等人[37]和Wu等人[32]分别提出了处理采用8-bit的S盒密码算法的模型.

与字节级MILP模型类似，比特级MILP模型引入0,1表示比特差分，1代表比特差分非0，0代表比特差分为0.

对于异或操作建模过程为：设a,b,c是异或操作的输入和输出差分，即a⊕b=c.对于比特级操作而言，(a,b,c)∈{(0,0,1),(0,1,0),(1,0,0),(1,1,1)}这4种情况是不可能出现的，故有如下约束关系：

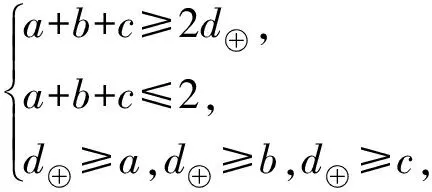
其中虚拟变量d⊕∈{0,1}.

对于S盒操作建模过程为：首先引入一个虚拟变量At∈{0,1}来表示S盒是否活跃，当且仅当S盒的输入差分不全为0时，At=1，反之At=0.目标函数即为

设(x0,x1,…,xμ-1)和(y0,y1,…,yν-1)是一个状态为μ×ν的S盒的基于比特的输入差分和输出差分，则对S盒建模有约束：

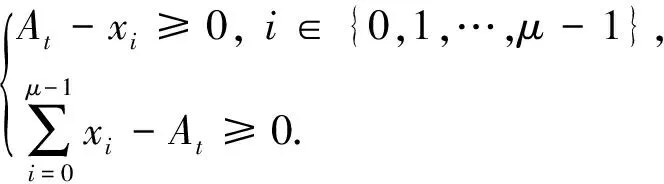
对于双射S盒，当输入差分非零，输出差分一定非零，则有约束：

与字节级建模不同的是，比特级建模增加了对S盒差分传播特性的建模，主要有2种方法：基于凸包的H-representation、基于布尔函数的和乘积问题.

1)基于凸包的H-representation建模

首先把S盒所对应的差分模式记为形如(x0,x1,…,xμ-1,y0,y1,…,yν-1)的离散点，然后使用软件SageMath生成形如α0x0+α1x1+…+αμ-1xμ-1+β0y0+β1y1+…+βν-1yν-1+c≥0的线性不等式.由于线性不等式的个数影响后续模型求解效率，因此需要减少线性不等式的数量，可采用贪心算法[34]或者MILP删减算法[36]来删去冗余的线性不等式.本文采用MILP删减算法[36].相比而言，贪心算法是启发式算法，不能得到最优解，MILP删减算法可以得到最少数量的线性不等式，也可以得到指定数目的不等式组.

值得注意的是，软件SageMath能够最快处理的离散点维度是12，因此这一方法最多能建模的S盒状态为6×6，故此建模方法多用于分析4-bit的S盒的密码算法.

2019年，吴文玲等人[32]提出了可以建模8-bit的S盒差分分布表的新方法，该方法基于2个观察，本文将其概括为引理1和引理2，推导过程见文献[32].

引理1[32].假设线性不等式f=λ0x0+λ1x1+…+λn-1xn-1+θ可以排除m个n维不可能差分模式，设δ为线性不等式f的负系数的和，θ为常系数.如果它存在一个位置，其对应的不可能差分模式都等于1或0，则相应的系数值为λ或-λ.即有：

λ=δ+θ.

引理2[32].假设线性不等式f=λ0x0+λ1x1+…+λn-1xn-1+θ可以排除m个n维不可能差分模式，设δ为线性不等式f的负系数的和，θ为常系数.如果将不可能差分模式扩展到n′位，其中扩展位置的值都等于1或0，那么，可以排除m个n′维不可能差分模式的新不等式.f′中扩展位置的系数值等于δ+θ或-(δ+θ)，而常系数θ′等于λ-δ′，其中θ′为新不等式f′的负系数之和，其余的系数不变.

文献[32]方法的思想是选择某些位作为变量，平均将差分分布表划分为多组，每组分别使用软件SageMath生成的低维凸包的H-representation，再根据引理1和引理2计算出所选变量在新的线性不等式中对应位置的系数的值，进而得到大状态S盒的差分传播特性对应的线性不等式.

2)基于布尔函数的和乘积问题建模

Abdelkhalek等人[37]将S盒差分分布表建模问题归为布尔函数的和乘积问题，提出建模8-bit的S盒差分传播特性的新方法.

设布尔函数f的和乘积表示为

其中x=(x0,x1,…,xn)和y=(y0,y1,…,yn)分别表示S盒的输入差分和输出差分，当且仅当输入差分和输出差分是可能差分模式时，f(x,y)=1，反之f(x,y)=0.首先将差分分布表转化为真值表，再使用软件Logic Friday来最小化布尔函数f的和乘积的项的数量，和乘积的每一项都代表一个线性不等式.该方法易于实现，但生成的线性不等式数量非常多.

2.3 改进基于大状态S盒密码算法的MILP模型

结合文献[32,37]的推理和分析，本文采用凸包的H-representation原理、布尔函数的和乘积问题原理相结合的方式来建模大状态S盒的差分传播特性.

定义1.pb-DDT.对于给定的S盒和它的DDT，如果在DDT中输入的概率为pb，则pb-DDT的对应数值为1，否则，pb-DDT的对应数值为0.

首先将DDT根据概率值的不同分为若干个pb-DDT，对于数值最小的一个pb-DDT，采用布尔函数的和乘积问题原理建模.对于其他的pb-DDT，基于凸包的H-representation原理和文献[32]提出的2个引理进行建模，本文对这部分建模的改进有3点：1)添加筛选不等式这一步，仅需要保留符合引理1的线性不等式；2)为了提高模型计算效率，需要2次删减冗余线性不等式；3)添加验证不等式这一步，排除编程失误的干扰，提高不等式准确性.详细建模过程有7步：

1)pb-DDT分组.记差分模式为(x0,x1,…,x7,y0,y1,…,y7)，选取前4位作为扩展变量(x0,x1,x2,x3)，则该pb-DDT被分成了16个分组，记录16组形如(x4,x5,…,x7,y0,y1,…,y7)的可能差分模式.

2)生成线性不等式.将记录的16组可能差分模式用软件SageMath处理，得到16组线性不等式.

3)筛选不等式.参考算法1来筛选线性不等式，得到符合引理1的线性不等式.

算法1.基于引理1的筛选算法.

输入：需要筛选的线性不等式组F；

输出：筛选后的线性不等式组Fcut.

①/*将线性不等式的负系数之和记为δ，常系数记为θ，任意系数记为λ*/

② functionscreen_algorithm(F)

③ forF中的线性不等式Fido

④ if 任意系数λ=δ+θ或-λ=δ+θthen

⑤ 将线性不等式Fi放入Fcut;

⑥ end if

⑦ end for

⑧ return 所有符合条件的线性不等式Fcut;

⑨ end function

4)扩展不等式系数.参考算法2，在原线性不等式上扩展(x0,x1,x2,x3)位置所对应的系数，生成新的线性不等式.

算法2.基于引理2的扩展算法.

输入：需要扩展的线性不等式组F；

输出：扩展后的线性不等式组Fextend.

①/*原线性不等式的负系数之和记为δ，原常系数记为θ，扩展后负系数之和记为δ′，扩展后常系数记为θ′*/

② functionextend_algorithm(F)

③ forF中的线性不等式Fido

④ if 扩展变量为1 then

⑤ 此位置的系数为-|δ+θ|,常系数

θ′=-θ;

⑥ end if

⑦ if 扩展变量为0 then

⑧ 此位置的系数为|δ+θ|,常系数不变

θ′=θ;

⑨ end if

⑩ end for

5)删减冗余不等式.采用MILP删减算法，参考算法3，对每组不等式进行删减.注意这一步不需要让线性不等式的数量最小，否则可能需要大量的时间.可根据分析者能接受的时间情况来筛选不等式.

算法3[36].基于MILP的删减线性不等式算法.

输入：全部的不可能差分模式集合R、需要删减的线性不等式组N；

输出：删减后的线性不等式组Ncut.

①/*设置线性不等式组N中的每一个线性不等式Ni的标记变量为zi，zi∈{0,1},1≤i≤n*/

② functionreduce_algorithm(R,N)

④ forRj,Nido

⑤ ifRj*Ni<0 then

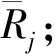
⑦ end if

⑧ end for

⑨/*删减部分，构造MILP模型求解Ncut*/

6)验证不等式.验证线性不等式是否正确，将16组可能差分模式代入16组线性不等式，检查是否全部符合，将16组不可能差分模式代入16组线性不等式，检查是否全部不符合.如果不成立，则说明实验代码有误，调整代码重新实验.

7)删减冗余不等式.全部的不可能差分模式和全部的线性不等式执行删减算法3，以删减冗余的线性不等式，从而得到刻画S盒所需要的全部线性不等式.之所以执行这一步，是因为算法1的步骤⑤没有获得数量最少的线性不等式，所以执行本步骤来进一步删减冗余的线性不等式.

3 搜索SM4算法的差分特征

3.1 构建SM4算法的MILP模型

首先，搜索活跃S盒个数，本文分别按照文献[32]和文献[37]的模型得到线性不等式，使其能够描述S盒的差分传播特性.其中使用文献[37]的模型得到8 282个线性不等式，使用文献[32]的模型得到3 987个线性不等式.在一定程度上，线性不等式数量越多，模型求解所耗费的时间也越多.尤其是当分析的轮数大于8轮时，求解时间较长，所以本文采用字节级建模来搜索SM4算法的活跃S盒下界.

根据2.1节所述的字节级MILP模型，并参考文献[32]所提出的性质，将其转化为线性不等式引入本文的模型，来评估1～24轮SM4算法的活跃S盒下界.特别地，对于SM4算法的19轮，为了接下来更迅速地得到高概率差分特征，需要增加如下2点约束：

1)在程序中手动设置19轮最小活跃S盒个数为18，且限制每轮的活跃S盒数量满足m1=[1,0,0,1,1,0,0,1,1,0,0,1,1,0,0,1,1,0,0]或者m2=[0,0,1,1,0,0,1,1,0,0,1,1,0,0,1,1,0，0，1]，即当m[i]=1时，第i轮活跃S盒个数为1，当m[i]=0时，第i轮活跃S盒个数为0.这2种模式下，可以搜索到概率为2-124的差分特征.

2)在程序中手动设置19轮最小活跃S盒个数为19，且限制每轮的活跃S盒数量满足m3=[1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1，1，1]，即当m[i]=1时，第i轮活跃S盒个数为1，当m[i]=0时，第i轮活跃S盒个数为0.该模式下，可以搜索到概率为2-123的差分特征.

在搜索高概率差分特征时，使用2.3节的模型，先对S盒建模，即生成能够刻画S盒差分传播概率特性的一组线性不等式，再对整体密码算法进行建模.

由表1知，SM4算法的DDT中有2种非0的概率，分别为2-6和2-7，对应的输入差分对个数分别为255和32 130，依据本文的改进模型，可以将DDT分为2-6-DDT和2-7-DDT.

对于2-6-DDT，按照2.3节所述，转化为布尔函数的和乘积问题，使用软件Logic Friday生成355个线性不等式.

同样对于2-7-DDT，按照2.3节所述建模，记差分模式为(x0,x1,…,x7,y0,y1,…,y7)，建模相关数据如表2所示，过程有7步：

1)2-7-DDT分组.选取(x0,x1,x2,x3)作为扩展变量，(x4,x5,…,x7,y0,y1,…,y7)作为固定变量，则可以生成16个分组.

2)生成线性不等式.使用软件SageMath分别处理这16个分组，生成16组线性不等式.

3)筛选不等式.参考算法1，依次对每组线性不等式进行筛选处理.

4)扩展不等式系数.参考算法2，扩展每组线性不等式的前4 b对应位置的系数，生成完整的线性不等式.

5)删减冗余不等式.参考算法3，对每组不等式进行去冗余.为了节省时间，本文没有去求解数量最少的线性不等式组.本文第1组生成线性不等式数量为239，其余15组线性不等式数量为249.

6)验证不等式.将16组可能差分模式代入16组线性不等式，检查是否全部符合.将16组不可能差分模式代入16组线性不等式，检查是否全部不符合.如符合，经验证本文生成的线性不等式是正确的.

7)删减冗余不等式.将16组线性不等式合并为1组，执行删减算法3，寻找更少数量的线性不等式.实验发现，在可接受的时间内，本文未找到数量更少的线性不等式组.

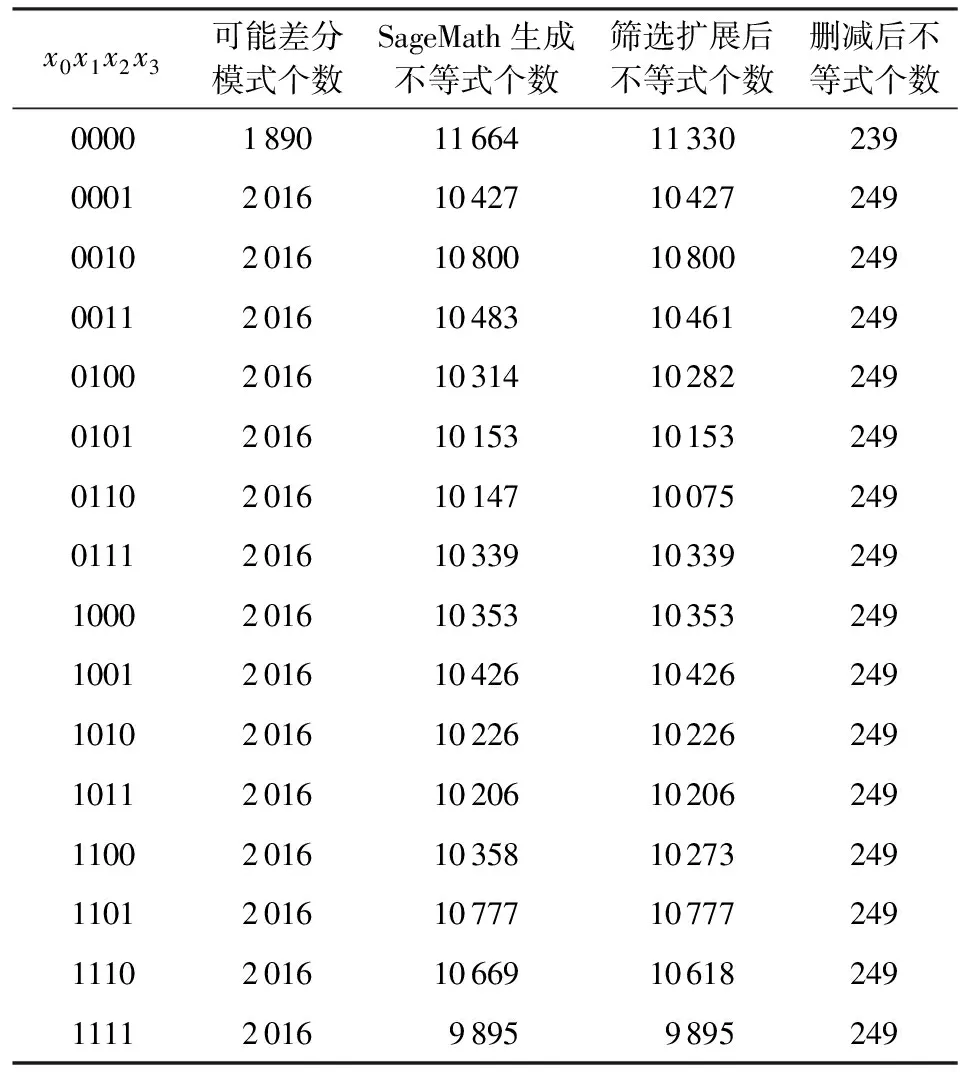
Table 2 2-7-DDT Differential Propagation Probability Modeling Data of SM4 Algorithm

综上，生成了刻画S盒差分传播的线性不等式，结果如表3所示:

Table 3 S-box Differential Propagation Probability Modeling Data of SM4 Algorithm

利用模型的条件约束[38]将2-6-DDT和2-7-DDT相应的所有线性不等式添加到模型中：

〈a,(x,y)〉+M(1-Qpb)≥b,

其中a为线性不等式系数，b为常数，M=2n，n为密码算法的分组状态.

最后，将第1步搜索出的结果作为输入，设置目标函数为Minimize:∑-log 2pbQpb,其中pb为差分成立的概率，Qpb∈{0,1}是标记概率的二进制变量，至此完成构建搜索高概率差分特征的模型.

3.2 实验结果

本文用Python语言实现了3.1节所述的模型，使用了GUROBI求解器，计算机配置为Intel®CoreTMi7-10700 CPU，2.90 GHz，16.00 GB RAM，16核，Win10系统.本文给出了1～24轮SM4算法的最小活跃S盒个数的下界和19轮SM4算法概率为2-123的差分特征，结果如表4和表5所示.

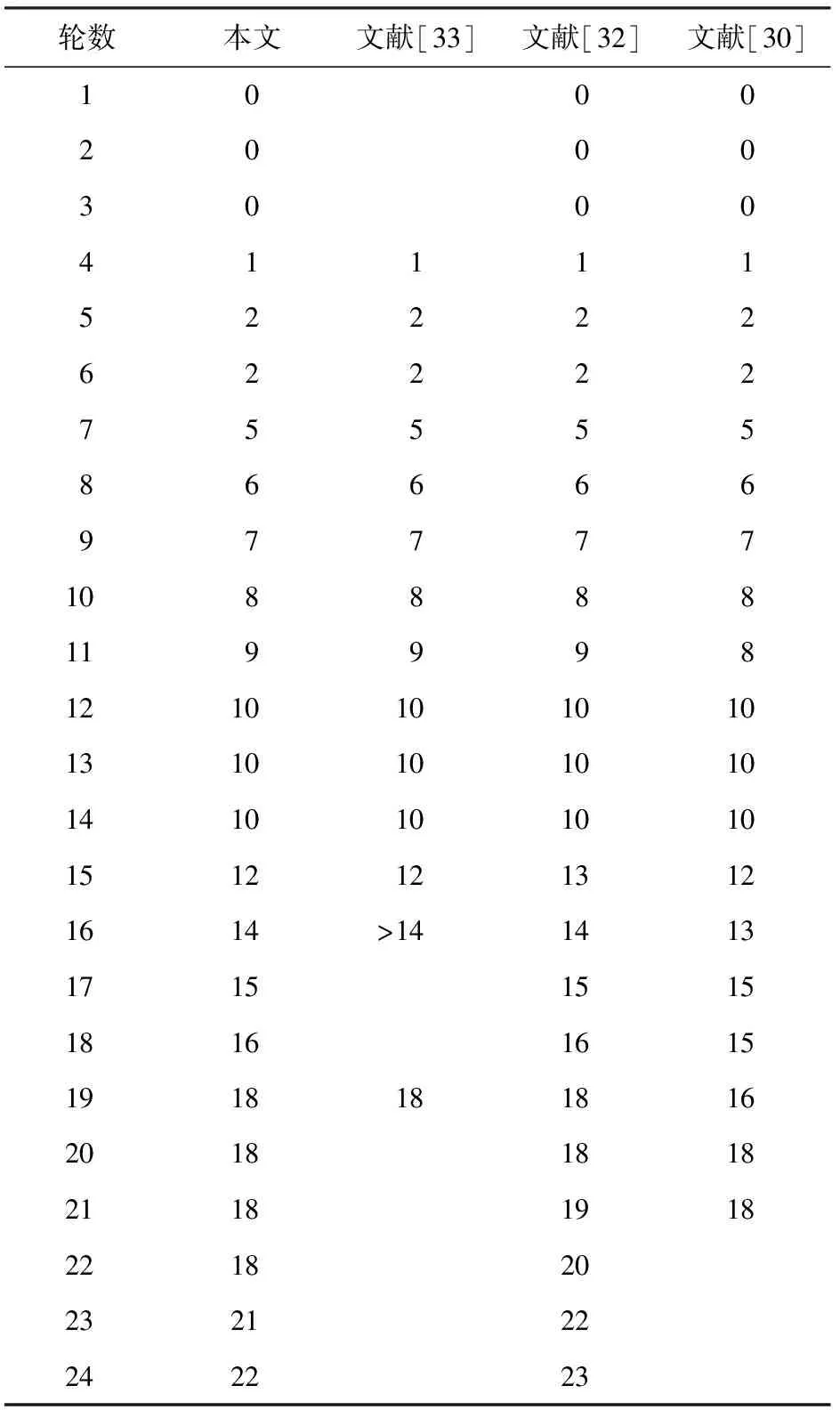
Table 4 Lower Bound on the Number of Active S-boxes for Different Rounds of SM4 Algorithm

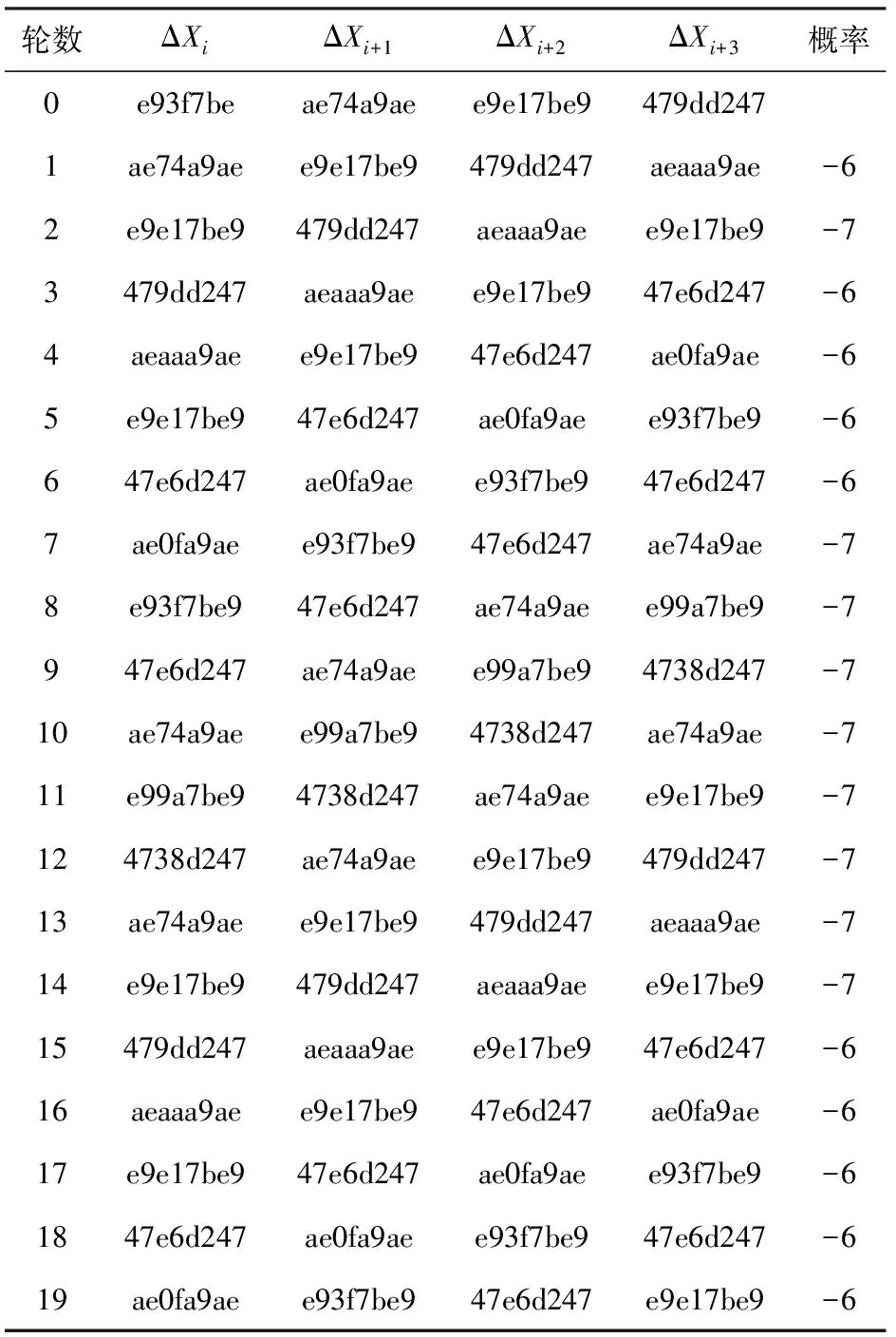
Table 5 A Differential Characteristic with Probability of 2-123 of 19-round SM4 Algorithm

随着轮数的增多，模型中的线性不等式个数也会增多，GUROBI求解模型的时间就越长.比如求解1～12轮的结果仅需要几秒到一分钟的时间，但求解大于19轮的结果需要几个小时甚至十几个小时.

与目前公开的结果相比，本文得到的活跃S盒个数的下界更紧.对于20轮SM4算法，当活跃S盒个数为18时，经过一个月时间的搜索，没有找到高概率的差分特征.对于21～24轮SM4算法，本文的结果小于论文给出的结果[31]，由于时间与计算机性能的原因，还未寻找21～24轮SM4算法的差分特征.尽管如此，24轮SM4的活跃S盒个数至少为22个，而SM4算法的S盒最大的差分概率是2-6，所以前24轮SM4差分特征的概率小于2-128.

当活跃S盒个数为18时，本文找到了19轮SM4概率为2-124的差分特征.当活跃S盒个数为19时，本文用5周的时间找到了一条19轮SM4概率为2-123的差分特征.经验证，该条差分特征是成立的.本文的结果表明高概率的差分特征对应的活跃S盒个数不一定最少.

4 总 结

就轮数而言，SM4算法目前公开的最好的差分特征是基于STP建模找到的19轮概率为2-123的差分特征.本文基于凸包的H-representation原理、布尔函数的和乘积问题，改进了搜索大状态S盒密码算法差分特征的方法，得到了1～24轮SM4算法活跃S盒个数更紧的下界，找到了19轮SM4算法概率为2-123的差分特征.该差分特征与目前公开的差分特征不同.在未来，我们将进一步优化模型，并用于搜索20轮SM4算法的差分特征，以及分析其他采用8-bit S盒的密码算法.

作者贡献声明：潘印雪负责方案的讨论、部分代码的编写以及论文撰写；王高丽指导方案的拟定和整体分析，把握论文创新性，并审阅修订论文；倪建强负责部分代码的编写.