基于NAR神经网络的人口数量预测方法

许晨

(中国石油集团东方地球物理勘探有限责任公司，河北 涿州 072750)

0 引 言

人口问题一直是影响城市发展与国土空间格局的重要因素，人口的规模会影响经济、社会的发展及资源的利用。不论人口问题、资源问题还是环境与发展问题，最终都是因为人口数量失控而引起的。因此科学地预测人口有助于合理制定符合实际需求的远景规划，保持适度的人口规模是经济、社会、资源和环境保护协调发展的强有力保证。因此，人口规模的预测及控制是各个国家重点研究和关注的问题。但是人口数量的变化受自然环境、社会环境、文化观念、医疗水平、政策导向等多种因素的影响，很难用一个确定的数学模型去描述。

目前预测人口数量的方法主要有人口年增长法、灰色预测模型、回归模型、logistic模型、马尔萨斯模型、时间序列法、修正指数曲线、人口指数增长模型、神经网络模型等方法。但目前所采用的方法大多具有一定的限制条件，如logistic模型需要较大的样本量，并且在人口出现负增长的时候无法预测；马尔萨斯模型相对简单，计算起来方便，但是其考虑的因素比较单一；灰色预测模型适用于小样本数据即短期人口数量预测，且对于不均匀增长趋势的人口序列预测效果并不明显。

神经网络算法(Artificial Neural Network, ANN)是一种受生物神经系统启发而来的数学模型，具有强大的非线性映射能力。可较好的表征数据间的复杂关联，拥有良好的数据处理能力且对样本数据的质量要求较低，运算灵活机动。因此，在数据处理与运算方面得到了广泛的使用。非线性自回归（Nonlinear Auto Regressive, NAR）神经网络是一种用于分析时间序列的动态神经网络模型。从本质上来说，是以时间序列自身作为回归变量，通过一段时间内的变量值的线性组合来表示之后某一时刻的变量值。相较于BP神经网络，NAR神经网络在信息传递过程中会向上一层进行反馈，参与下一层计算。因而，其输出并不只是一种静态的映射，还是之前动态结果的综合利用。NAR神经网络在提出之后在时间序列分析、预测领域均得到了广泛的应用。本文将探讨利用NAR神经网络模型进行人口总数预测的方法与效果。

1 NAR神经网络

NAR(Nonlinear Auto-Regressive)神经网络全称为非线性自回归模型，属于动态神经网络中的一种。模型的输入输出之间的变量关系并不仅仅是一种静态方式的映射，每一时刻的输出都是基于当前时刻以前系统的动态结果综合而得，即具有反馈和记忆的功能。使该神经网络同时具备动态和完整系统信息的特征。因而NAR神经网络不仅继承了传统时间序列模型的优点，对于非线性数据具有更好的适应能力和预测效果。NAR神经网络的模型可描述为：

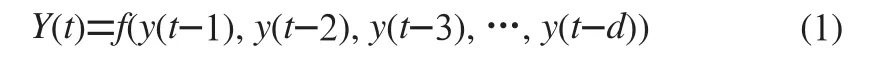
式中：()为当前时刻的变量值；((-1),(-2),(-3),…,(-)为历史时刻的变量值；为延迟阶数。

一般情况下，NAR神经网络由静态神经元与网络输出反馈两部分组成。一个完整的NAR神经网络一般由输入层、隐含层、输出层构成，如图1所示，数据()由输入层进入，进入隐藏层，经过训练、传递、学习之后到达输出层，进而得到预测结果。

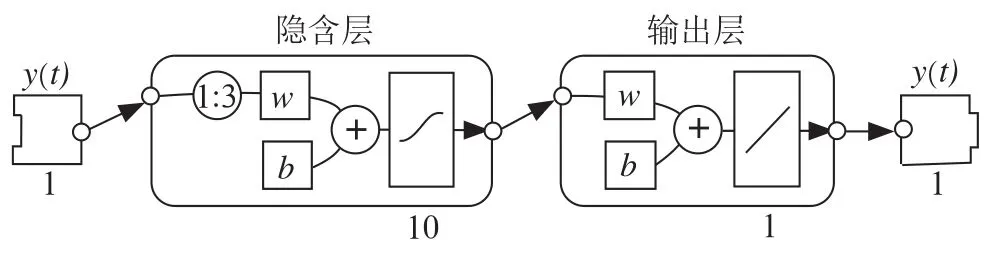
图1 NAR神经网络

图中，()表示神经网络的输入；隐藏层中的1:3为延时阶数，表示利用时间序列中某一点前的三个点来预测该点的值；为连接权，为阈值。各个神经元输出可表示为：

式中：为激活函数；w为第个输出时延信号和隐含层第个神经元之间的连接权值。

2 实例研究

本文拟利用NAR神经网络进行中国人口数量预测，图2为1949年—2017年中国总人口数量统计，数据来源为中国统 计 局（https://data.stats.gov.cn/easyquery.htm?cn=C01）。从图中可以看出自1949年以来，除1960年左右存在一个小规模的下降阶段外，我国人口总量整体呈逐年上升趋势，至2017年底全国人口总数接近14亿。

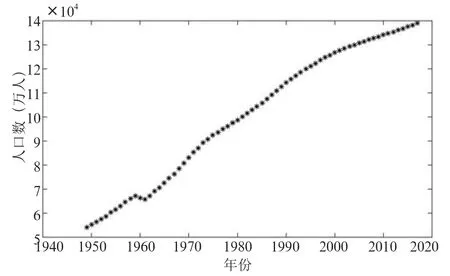
图2 1949—2017年中国人口总数

利用1949年—2010年之间的62个数据作为神经网络训练样本，将2011年—2017年之间的7个数据作为验证样本。其中训练样本中70%参与神经网络训练(training)；15%进行交叉检验(validation)；剩余15%进行测试(test)。本文所构建的NAR神经网络延时阶数为3，即利用时间序列中某一点的前3个点来预测该点数值；隐藏层神经元个数为10；最大迭代次数为1 000。在NAR神经网络训练阶段，利用训练集中数输出据输出与原始数据相关系数和训练误差的Ljung-Box Q检验来确定训练所得的神经网络是否可靠。图3为最终采用的神经网络模型的训练误差图。该神经网络在迭代15次之后，误差即达到最小。从图3可以看出训练输出(蓝色)、交叉检验输出(绿色)与测试输出(红色)均与原时间序列具有较高的吻合度。且训练集中数输出据输出与原始数据相关系数为0.99，Ljung-Box Q检验结果为0。表明该神经网络较为可靠，可用于下一步预测。

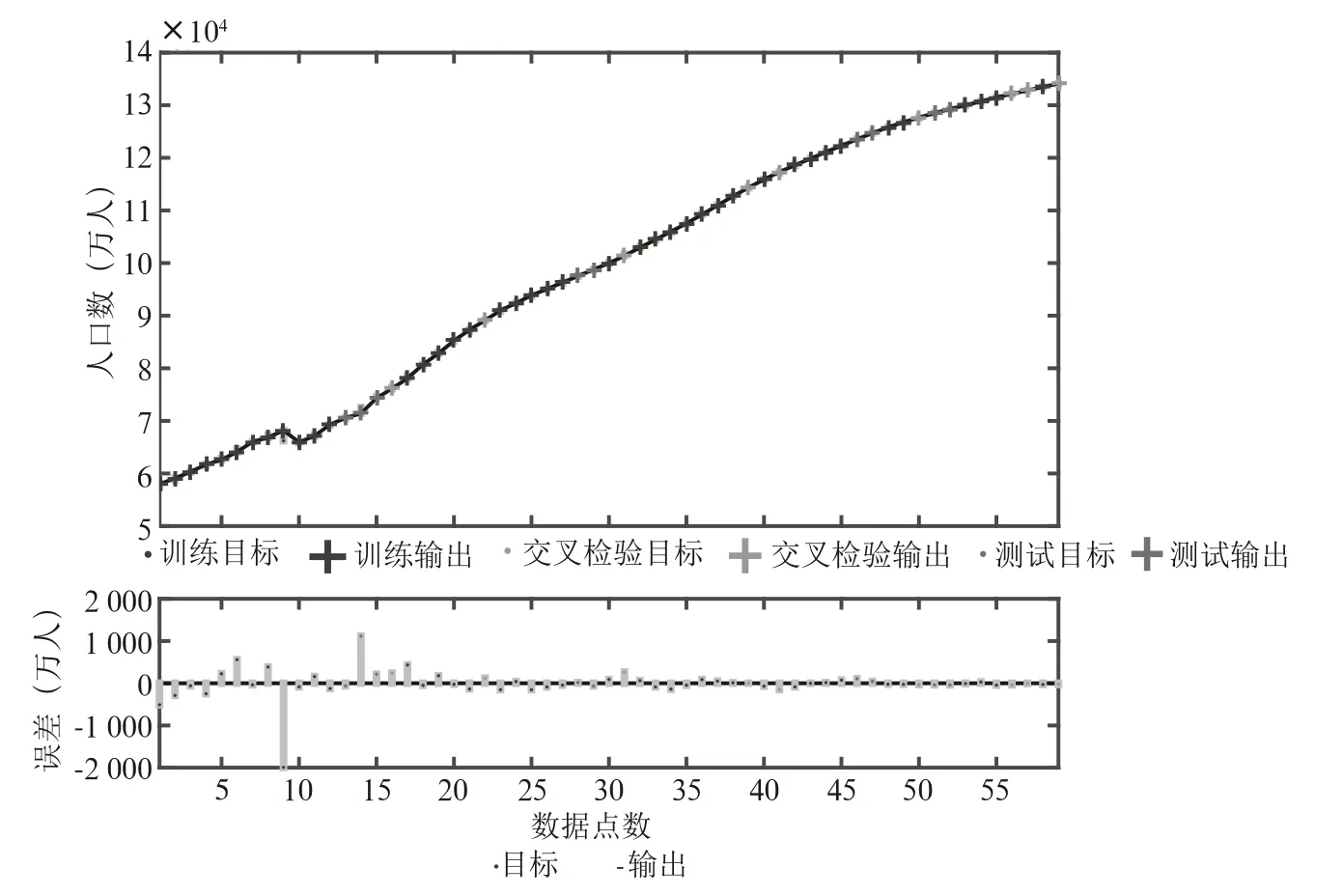
图3 NAR神经网络训练误差

在训练得出可靠的神经网络之后，即可进行预测。图4(a)为预测结果图4(b)为预测误差。从图中可以看出利用NAR神经网络预测获得的2011年—2017年人口总数与实际人口数量具有较高的吻合度。预测绝对误差在50万人之内。因而利用该神经网络模型可进一步预测全国人口总数的规模及趋势。

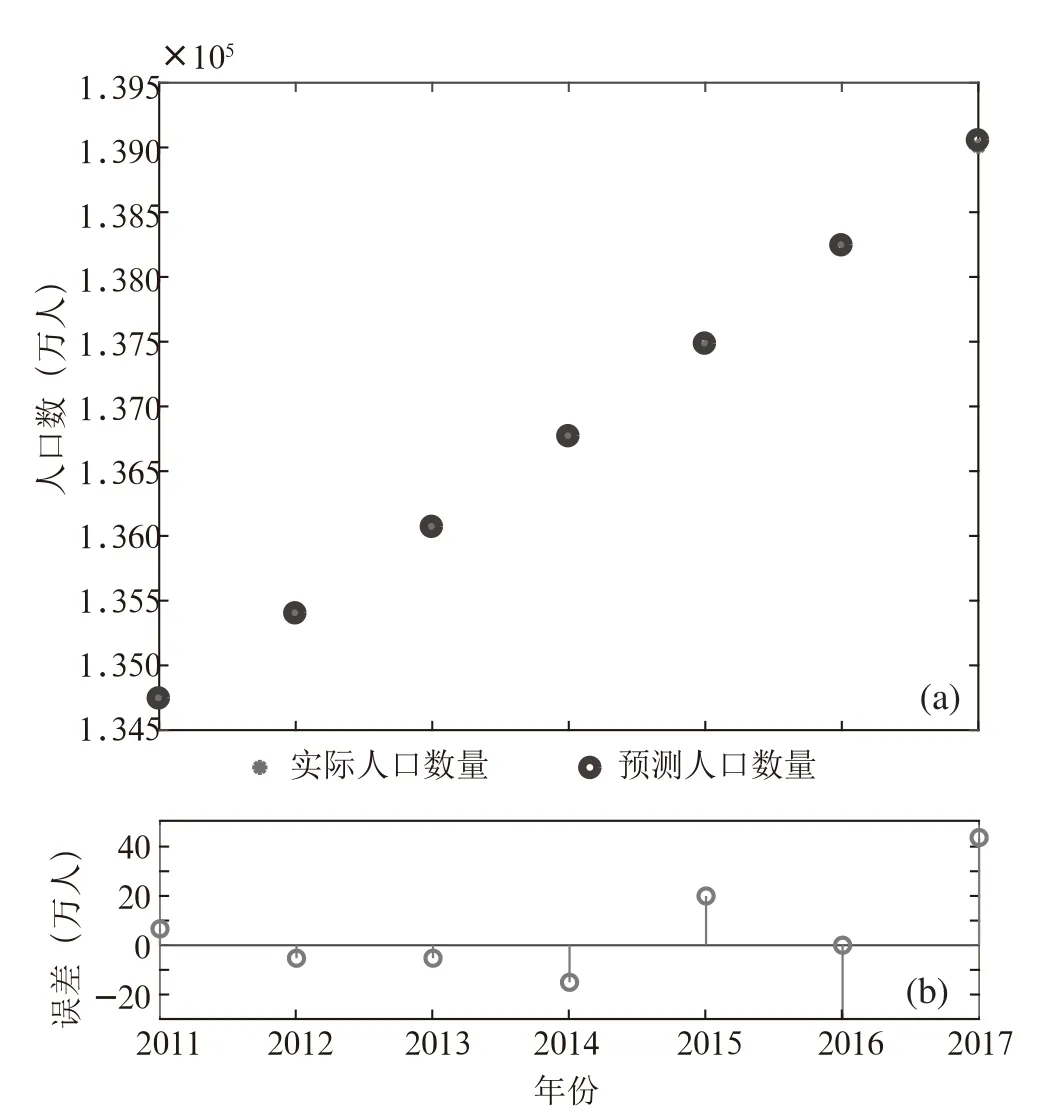
图4 NAR神经网络预测结果

3 结果与讨论

本文利用NAR神经网络模型，以1949年—2010年人口数为训练样本，对我国2011—2017年人口数量进行了预测，从对比结果来看具有较高的预测精度。而在利用NAR神经网络进行时间序列预测时，需设置两个参数：延时阶数和隐藏层神经元个数。本文在进行预测时，延时阶数为3，隐藏层神经元个数为10。但目前对于以上两个参数的设置尚无有明确的标准，通常情况下是根据经验给出相应参数值。

为了研究不同延时阶数与隐藏层神经元的个数对于预测结果的影响，本文分别设置了延时阶数分别为5和10、隐藏层神经元个数分别为5和10的不同神经网络模型对人口数据进行预测。测试结果如图5所示。其中图5(a)为延时阶数和隐藏层神经元个数均为10时的预测结果；图5(b)为延时阶数为5、隐藏层神经元个数为10时的预测结果；图5(c)为延时阶数为10、隐藏层神经元个数为5时的预测结果；图5(d)为延时阶数和隐藏层神经元个数均为5时的预测结果。

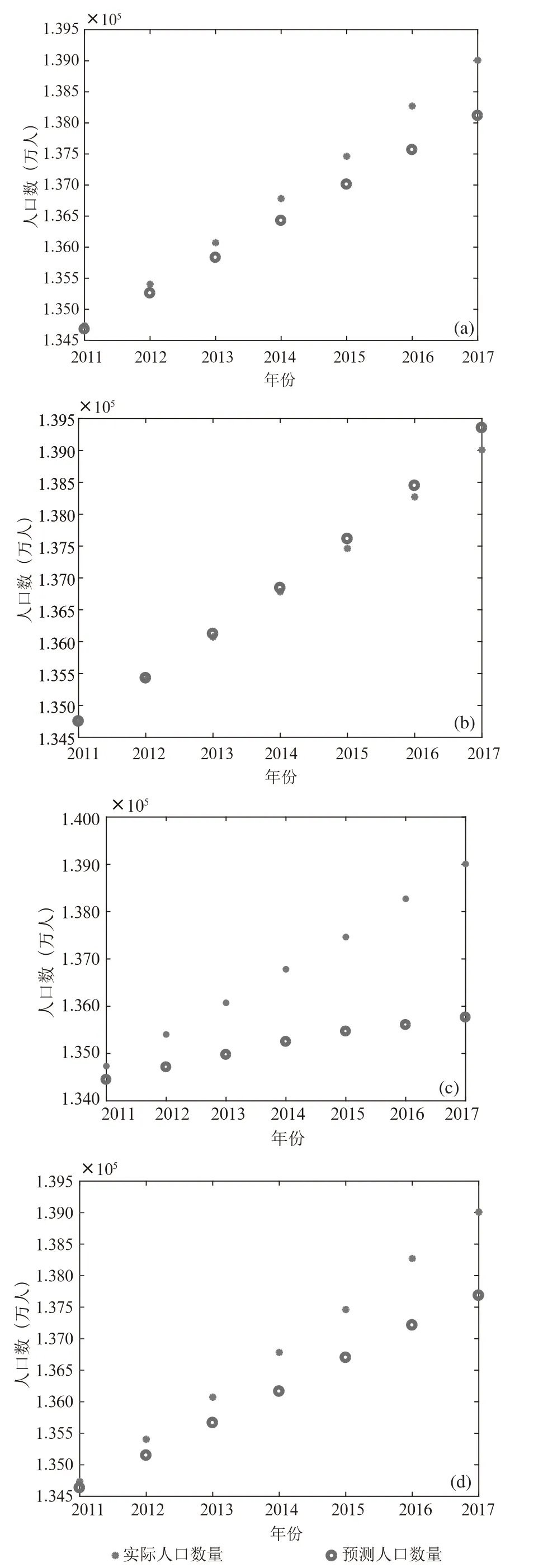
图5 不同延时阶数和隐藏层神经元个数预测结果对比

从预测结果对比中可以看出当隐藏层神经元个数相同时，随着延时阶数的增加预测误差在增大；而当延时阶数相同时，隐藏层神经元个数越少预测误差越大。

从以上测试结果可以看出，延时阶数和隐藏层神经元个数的选择对于最终预测结果具有较大的影响。当选择不当式，可能会造成较大的预测错误。因此在利用NAR神经网络进行预测时应当留出部分数据作为验证数据，通过预测结果与验证数据之间的误差来控制参数选取，以期获得较为准确的预测结果。

4 结 论

本文以1949年—2010年人口总数作为输入，利用NAR神经网络模型对我国2011年—2017年人口总数进行了预测，预测结果与实际人口总数吻合程度较高。主要得出以下结论：

（1）利用NAR神经网络模型进行人口数量预测，无需对原时间序列进行过多的预处理操作，且收敛速度较快，使用方便。根据预测结果与实际人口数的对比，其预测结果具有较高的准确性。

（2）NAR神经网络模型预测结果受延时阶数和隐藏层神经元个数影响较大。因此，在进行预测时应当充分利用先验信息进行约束和检验。选取合理的参数设置，从而获得更加可靠地预测结果。