安徽省城镇居民人均可支配收入组合预测

张文扬， 汪 凯， 袁宏俊

(安徽财经大学 统计与应用数学学院，安徽 蚌埠 233030)

0 引 言

十四五规划明确指出了“推进以人为核心的新型城镇化”。城镇居民人均可支配收入增长趋势可以在一定程度上反映出城镇化效率。近年来，随着经济发展水平的提高，城镇居民人均可支配收入结构逐渐向多元化转变，城镇居民人均可支配收入的增加意味着城镇居民生活水平的提升。《安徽省2020年国民经济和社会发展统计公报》指出，2020年安徽省城镇居民人均可支配收入为39 442元，同比上年增长5.1%，可以看出安徽省城镇居民人均可支配收入正处于增长态势，疫情冲击未造成过大影响，城镇居民生活水平正逐步改善。

国内学者对于城镇居民人均可支配收入的研究主要从两个维度出发，一是探究城镇居民人均可支配收入的驱动机制：陈江磊[1]基于2009—2019年陕西省城镇居民消费与支出数据构建VAR模型，探究陕西省居民消费与支出发展关联性，研究发现陕西省城镇居民消费支出对居民人均可支配收入有正向促进作用，相反，城镇居民人均可支配收入对消费支出有一定抑制作用；王敏等[2]应用灰色关联度分析法探究2007—2017年上海市城镇居民人均可支配收入与不同消费支出间关联度，研究发现上海市城镇居民消费结构正从生活型消费逐步转变为享受型消费；熊华平等[3]应用格兰杰因果关系检验对1985—2011年我国房屋年竣工面积与城镇居民人均可支配收入两个时序数据进行建模分析，研究表明我国城镇居民人均可支配收入是房地产业发展的Granger原因，而房地产业发展对城镇居民人均可支配收入提高的作用并不明显[3]。二是对城镇居民人均可支配收入进行预测:滕秀花等[4]应用灰色Markov模型进行安徽省城镇居民人均可支配收入预测，研究表明灰色Markov模型预测精度较高，2019，2020年预测值分别为37 875.24元和41 654.8元；李新朋等[5]基于1985—2017年上海市城镇居民人均可支配收入相关数据，构建ARIMA(1,1,0)模型并对2018年上海市城镇居民人均可支配收入进行预测，研究发现ARIMA(1,1,0)模型预测偏差较低，2018年上海市城镇居民人均可支配收入预测值为67 371.61元；王振寰等[6]基于1978—2011年城镇居民家庭人均可支配收入相关数据，建立ARIMA模型进行时序分析，研究表明ARIMA模型预测效果较优；张婷婷[7]基于2000—2015年湖北省城镇居民人均可支配收入相关数据，构建ARIMA(0,2,0)模型并对未来10年湖北省城镇居民人均可支配收入进行预测，研究表明未来10年湖北省城镇居民人均可支配收入仍呈现上涨趋势。

综上所述，目前已有较多学者对城镇居民人均可支配收入进行预测，时间序列模型在预测时有一定的优越性，但大部分学者使用单项预测模型进行预测。尽管单项预测模型适用于小样本数据的精确短期预测，但单项预测存在一定的随机性，未能充分利用数据所反映的有效信息。鉴于此，为降低预测随机性，提升模型稳定性，提高预测精度，本文将误差平方和最小作为准则，结合GIOWA算子构建变权系数组合模型对安徽省未来5年城镇居民人均可支配收入进行短期预测，以期为正确制定城镇化发展战略提供一定参考和帮助。

1 单项预测模型

1.1 多元线性回归模型

1.1.1 指标选取和数据整理

通过查阅相关文献及资料，在指标选取的可比性、可得性与科学性原则下，选择城镇居民人均可支配收入(PCDI)为被解释变量，地区经济发展水平、地区产业结构、地区经济发展能力、地区贸易水平、人口发展速度、城镇居民就业水平、城镇居民消费水平为解释变量。各解释变量对应指标及符号表示如表1所示。

表1 解释变量指标名称及含义Table 1 Index names and meanings of explanatory variables

地区经济发展水平反映出地区经济发展的规模及速度，选用地区GDP进行度量。地区产业结构是指某一地区各产业的构成成分以及各构成成分间的联系和比例关系，选用第三产业所占比重进行度量。地区经济发展能力、地区贸易水平分别用固定资产投资额、进出口总额进行度量。人口发展速度会对城镇常住人口数产生一定影响，选用人口自然增长率进行度量。城镇居民就业水平会对工资性收入产生一定影响，用城镇登记失业率进行度量，城镇登记失业率越低，就业水平越充分；城镇登记失业率越高，就业水平越低效。居民消费水平反映了居民从获取基本生存资料逐步向享受及发展资料的转变趋势，城镇居民消费水平选用城镇居民人均消费支出进行度量。

为保证模型的科学性、可行性和稳定性，本文遵循数据的完整可比原则，基于2000—2020年安徽省相关数据进行研究分析。所有涉及数据均来自2000—2020年《安徽省国民经济和社会发展统计公报》及安徽省统计年鉴。

1.1.2 模型构建及应用

通过检验发现各解释变量间存在多重共线性，因此采用逐步回归法剔除多余变量以消除变量间多重共线性，进一步构建最优线性回归模型。将安徽省城镇居民人均可支配收入多元线性回归模型最终拟定为

EPCDI=40.317 7EIS+0.256 9EIIFA+0.759 1EPCE+

0.253 6EGDP

(1)

式(1)中，R2=0.999 7,F=12 470.92，说明模型拟合程度较优，精确度较高。

结合表2可以看出，解释变量EIIFA，EPCE,EGDP，EIS在显著性水平α=0.05的条件下显著。EIIFA，EGDP与EIS的回归系数符号为正，表明当地区经济发展水平提升、大力发展第三产业时，会在一定程度上提高城镇居民就业率，进而助推城镇居民人均可支配收入增加，符合经济学意义。EPCE的回归系数符号为正，说明城镇居民人均可支配收入与城镇居民人均消费支出间呈正相关，当城镇居民人均消费支出增加时，会在较大程度上促进城镇居民人均可支配收入增加，消费支出的增加反映了居民对更高生活水平的追求，生活水平的提升意味着居民消费能力也随之提高，更高的生活水平及消费能力需要更高的工资水平相匹配，消费支出增加同样会助推城镇居民人均可支配收入增加，也符合经济学意义和一般社会经济现象。

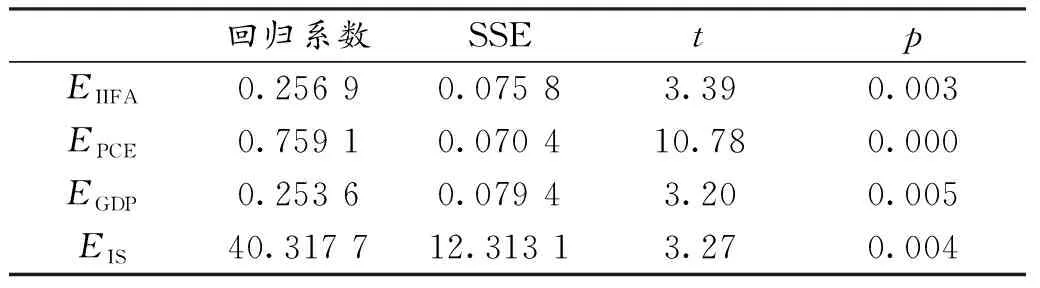
表2 解释变量显著性检验情况Table 2 Significance test of explanatory variables

应用式(1)，还可计算样本期内安徽省城镇居民人均可支配收入多元线性回归拟合值。

1.2 指数平滑预测模型

1.2.1 相关理论

指数平滑预测法是一种基于指标本期实际值和预测值，引入一个简化加权因子(即平滑系数，通常记作α)，以求得平均值的时间序列预测法。根据参数设置个数的不同分为一次指数平滑预测、二次指数平滑预测和三次指数平滑预测。

指数平滑预测的适用范围具有一定的局限性，通常运用一次指数平滑法对平稳时间序列进行预测；运用二次指数平滑法对存在趋势性特征的时间序列进行预测；运用三次指数平滑法对具有趋势性和季节性(周期性)特征的时间序列进行预测。

较少数据的时间序列中短期预测可以借由指数平滑法实现。

一次指数平滑模型：

(2)

进行一次指数平滑预测时，直接使用第t期一次指数平滑预测值作为第t+1期预测值。

二次指数平滑模型：

(3)

二次指数平滑模型的截距及斜率的计算公式分别为

1.2.2 模型构建及应用

使用数值分析工具Matlab绘制2000—2020年安徽省城镇居民人均可支配收入趋势图，见图1。

图1 2000—2020年安徽省城镇居民人均可支配收入趋势图Fig.1 Trend chart of per capita disposable income of urban residents in Anhui Province from 2000 to 2020

从图1可以看出：2000—2020年安徽省城镇居民人均可支配收入存在明显的线性增长趋势，因此可选择二次指数平滑预测法对安徽省城镇居民人均可支配收入进行短期预测，应用Stata 16计量软件进行二次指数平滑预测。

1.3 灰色Markov预测模型

1.3.1 相关理论

灰色系统理论[8]是由邓聚龙教授于1982年提出并加以发展的，以“部分信息已知，部分信息未知”的“小样本”、“贫信息”不确定系统为研究对象，通过开发部分已知信息提取有价值信息，充分利用已知信息探究系统运动规律，并据此进行科学预测[9]。GM(1,1)模型是灰色系统理论中较为基础的动态预测模型，应用较为广泛，通常适用于小数据量短期预测。

Markov过程是一类具有无记忆性的随机过程，根据状态间转移概率对系统未来发展进行预测。Markov转移概率预测常用于揭示系统在不同状态区间转移的内在规律。

1.3.2 GM(1,1)模型构建及应用

步骤1定义时间序列数据。以表3中2000—2020年安徽省城镇居民人均可支配收入实际值作为原始数据，按照时间顺序先后定义时间序列X：

X=(x1,x2,…，x21)

步骤2对时间序列X进行一次累加生成Y：

Y=(y1,y2,…，y21)

步骤3定义累加矩阵B与常向量M：

其中，

(4)

步骤4将式(4)中参数α，μ代入微分方程式(5)中求解，获得一次累加序列Y的预测模型：

(5)

通过计算，累加序列Y预测模型为

(6)

步骤5通过当期数值与上期数值逐项相减获得原始时间序列X预测值：

(7)

计算结果如表3所示。

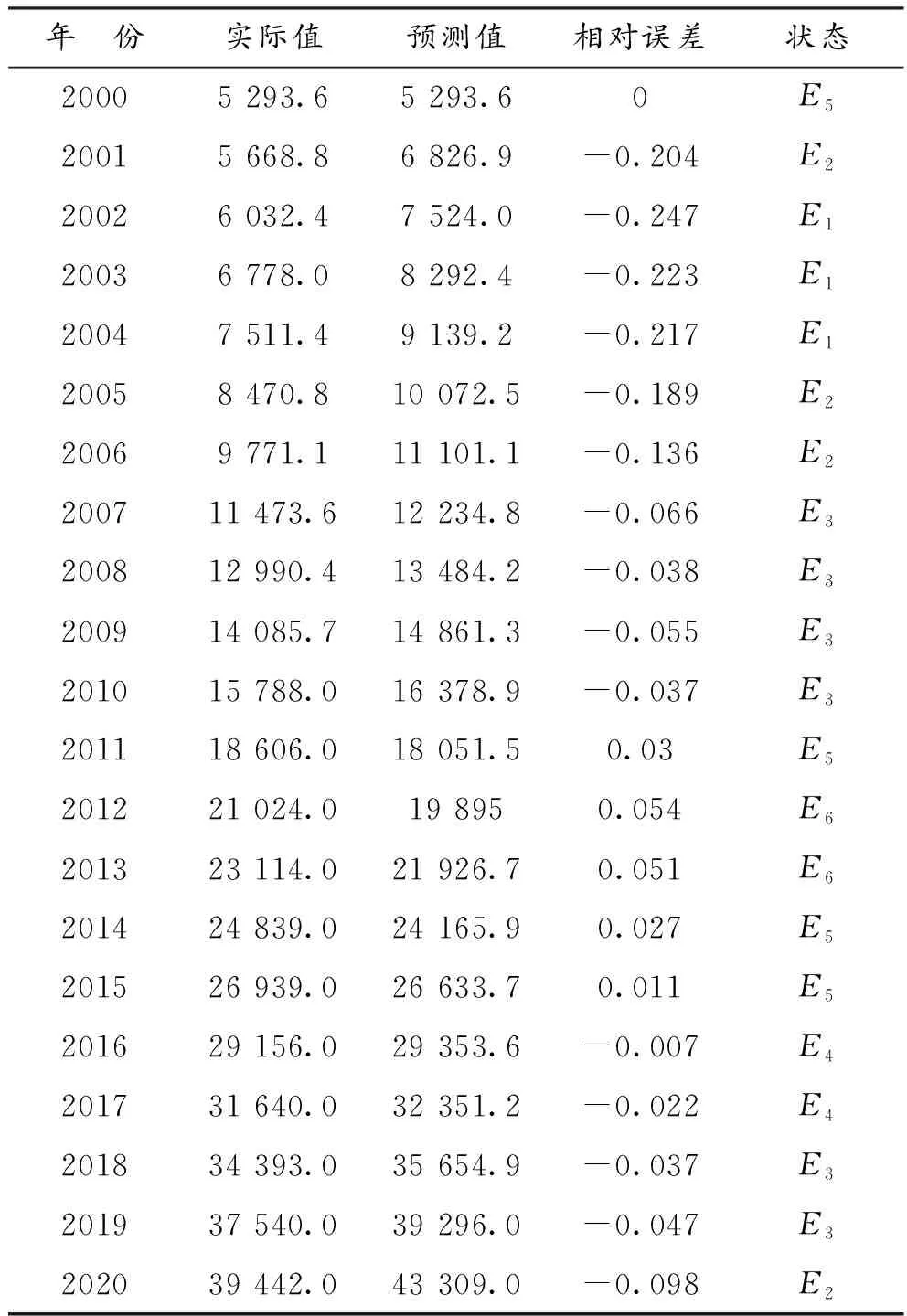
表3 GM(1,1)模型预测值及误差Table 3 Predicted values and errors of GM(1,1) model

以安徽省城镇居民人均可支配收入为研究对象，先用2000—2020年相关数据构建GM(1,1)预测模型，再用相关数据检验模型精度及预测效果，最后对2021—2025年安徽省城镇居民人均可支配收入进行灰色预测。

应用Matlab编程软件计算得到GM(1,1)模型待估参数α=-0.097 2,u=5 985.605 2，根据式(6)及式(7)计算得到GM(1,1)模型预测值及相对误差，如表3所示。

步骤1状态划分。

划分状态的数目由样本数量决定，状态数量越多，模型预测精度越高。任一状态Ei可表示为

其中，ai,bi赋值由研究对象相关数据确定。

本文根据安徽省城镇居民人均可支配收入实际数据，以及GM(1,1)模型预测相对误差情况，将收入数据序列划分为6个状态(表3)，具体划分如下：

步骤2状态转移矩阵构建。

构建1步转移矩阵时，鉴于2020年的转移状态未知，因此只考虑前20期的转移情况。落入6个状态区间的原始数据样本期数分别为3，3，6，2，4，2。在状态E1中，有2期经过1步转移后仍处于E1，有1期经过1步后转移到状态E2，1步转移到状态E3，E4，E5和E6的期数为0，故1步状态转移矩阵第一行为2/3,1/3,0,0,3,3。同理可求出矩阵剩下5行，1步状态转移矩阵为

二语学习者在习得一个语块后就能在语义上进行替换，创造出无数新鲜的内容，使语言具备产出性，也能够促进词汇深度知识的习得。构式语法理论不仅有助于教师创新教学模式，也有利于学生自主性学习模式的养成，提高军事英语词汇学习的质量，使他们能够产出更准确、更地道、更丰富的目的语语言。当然，我们也应该清醒地认识到，无论是语法教学法、词汇教学法、交际教学法还是任务型教学法，都有各自的优缺点，是可以取长补短、综合利用的。笔者日后还将进行更深入、更全面的研究，找到构式语法理论与其他教学法的最佳切合点，更有效地提高学生的军事英语应用能力。

同理，2步、3步、4步转移矩阵分别为

步骤3模型检验及预测。

根据马尔可夫预测理论，对2020年安徽省城镇居民人均可支配收入进行试预测，选择距离2020年最近的4个时段，转移步数分别定为4，3，2，1步。根据相应状态转移矩阵，基于各初始状态对应行向量构建状态预测概率矩阵，具体结果见表4。

表4 状态预测表Table 4 State prediction table

根据表4中状态转移概率矩阵列向量求和结果，可以发现2020年处于E2状态的可能性最高，结合GM(1,1)预测值，计算得到2020年安徽省城镇居民人均可支配灰色Markov模型预测值为42 146.6元，而实际值为39 442元，2020年灰色Markov模型预测值相对误差绝对值为0.068，小于2020年GM(1,1)模型预测值相对误差绝对值，在一定程度上提升了模型的预测精度。

根据表3的预测状态，结合GM(1,1)模型预测值，进一步计算灰色Markov模型预测值(表5)。

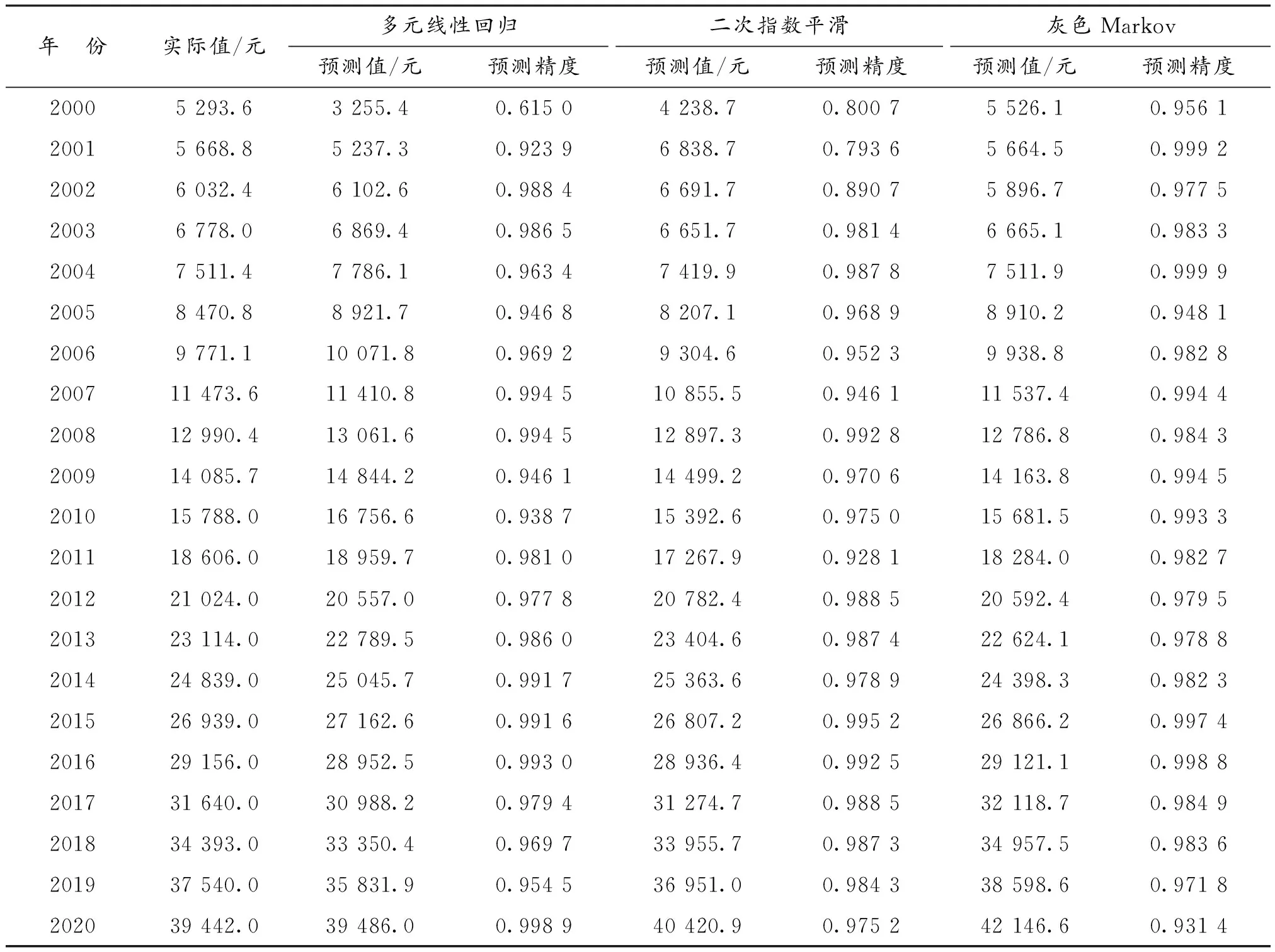
表5 单项预测模型预测值与预测精度Table 5 Predicted values and prediction accuracy of single prediction model

将3项单项预测模型2000—2020年安徽省城镇居民人均可支配收入预测值与实际值增长趋势进行比较分析，见图2。

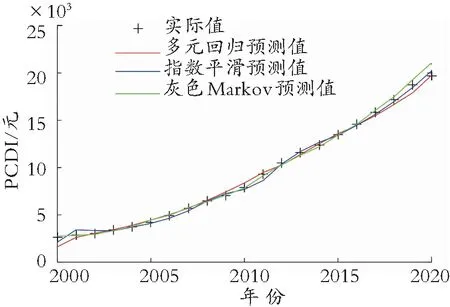
图2 单项预测模型预测值、实际值比较分析Fig.2 Comparison and analysis of the predicted and actual values of the single prediction model

结合表5和图2可以看出，相较于多元线性回归模型及指数平滑预测模型，样本期内灰色Markov模型预测精度更高，预测效果更优。

2 基于误差平方和及GIOWA算子的组合预测模型

组合预测法由美国学者Bates等[10]于1969年首次提出。针对同一问题应用两种及以上单项预测模型进行预测，分别赋予各单项预测模型合适的权系数，再将各单项预测模型预测结果按照权系数进行组合，合理且充分提取并使用各单项预测模型的有效信息，进一步优化模型预测效果，提高模型预测精度。为综合利用各单项预测模型预测结果，本文引入GIOWA算子，将单项预测模型预测精度作为诱导变量，将误差平方和最小作为计算准则[11]，构建变权系数组合预测模型，并对GIOWA算子分别取不同参数值λ，计算各模型最优权系数。

2.1 相关理论

2.1.1 GIOWA算子

在GIOWA算子基础上，对参数λ分别取不同值构建几种常见算子。

2.1.2 基于误差平方和及GIOWA算子的组合预测模型

假定针对某一问题进行预测时选用n种单项预测模型，记xt,xit,eit,uit分别表示序列第t期实际观测值、第i种单项预测模型第t期序列预测值、第i种单项预测模型第t期预测值绝对误差、第i种单项预测模型第t期预测精度，则预测精度uit为

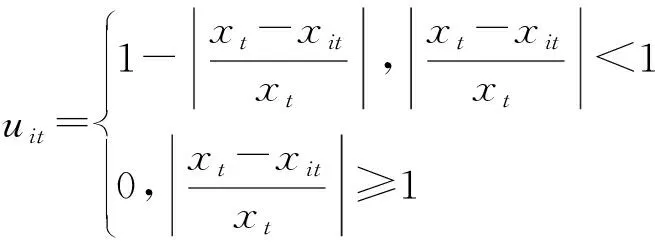
以预测精度uit为xit诱导变量，则n种单项预测模型第t期预测精度uit与第t期预测值xit构成二维数组(,,…)，GIOWA优化组合预测值为

为方便计算，诱导预测误差记为eu-index(it)=(xt)λ-(xu-index(it))λ，当参数λ取上述4种不同值时，诱导预测误差分别为

基于误差平方和及GIOWA算子的组合预测模型λ次幂误差为

基于误差平方和及GIOWA算子的组合预测模型λ次幂误差平方和为

(8)

基于误差准则，期望误差平方和最小，结合GIOWA算子，构建组合预测模型为

minQ=WTEW

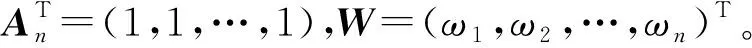
2.2 模型构建及应用

2.2.1 构建诱导有序加权算术平均(IOWA)组合预测模型

步骤1 通过计算获得诱导有序误差信息矩阵：

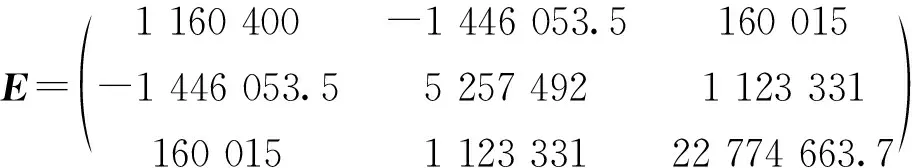
步骤2 将预测误差平方和最小化的IOWA组合预测模型转化为下述非线性规划模型：

minQ=WTEW=1 160 400ω12-2 892 107ω1ω2+

3 320 030ω1ω3+5 257 492ω22+

2 246 662ω2ω3+22 774 663.7ω32

(9)

运用LINGO 11.0软件对式(9)进行求解，权系数分别为

ω1=0.720 0,ω2=0.280 0,ω3= 0

步骤3 构建误差平方和最小的IOWA优化组合预测模型为

(10)

样本期内，式(10)组合预测误差平方和Q=430 689.9。式(10)表示对某一期3项单项预测精度最高、次高、最低单项预测值分别赋予0.72，0.28，0的权系数。

2.2.2 构建诱导有序加权几何平均(IOWGA)组合预测模型

步骤1 通过计算获得诱导有序对数误差信息矩阵：

步骤2 将对数误差平方和最小的IOWGA组合预测模型转化为下述非线性规划模型：

minQ=WTVW=0.004 9ω12-0.024ω1ω2-

0.036 5ω1ω3+0.064 9ω22+

0.185 3ω2ω3+0.312 2ω32

(11)

运用LINGO 11.0软件对式(11)进行求解，权系数分别为

ω1=0.820 0,ω2=0.179 5,ω3= 0.000 5

步骤3 构建对数误差平方和最小的IOWGA组合预测模型为

(12)

样本期内，式(12)组合预测对数误差平方和Q=0.001 8。

2.2.3 构建诱导有序加权调和平均(IOWHA)组合预测模型

步骤1 通过计算获得诱导有序倒数误差信息矩阵：

步骤2 将倒数误差平方和最小的IOWHA组合预测模型转化为下述非线性规划模型：

minQ=WTUW=9.085 1×10-11ω12-

8.037 4×10-10ω1ω2-1.885 2×10-9ω1ω3+

2.495 8×10-9ω22+1.013 6×10-8ω2ω3+

1.533 7×10-8ω32

(13)

运用LINGO 11.0软件对式(13)进行求解，权系数分别为ω1=0.864 5,ω2=0.134 3,ω3= 0.001 2。

步骤3 构建误差平方和最小的IOWHA组合预测模型为

(14)

样本期内，式(14)组合预测倒数误差平方和Q=2.059×10-9。

2.2.4 构建λ=0.5时诱导有序加权平均(GIOWA)组合预测模型

步骤1 通过计算获得诱导有序误差信息矩阵：

步骤2 将误差平方和最小的GIOWA组合预测模型转化为下述非线性规划模型：

minQ=WTMW=15.075 5ω12-47.597 6ω1ω2-

14.95ω1ω3+105.439 8ω22+

189.915 4ω2ω3+473.016 8ω32

(15)

运用LINGO 11.0软件对式(15)进行求解，权系数分别为ω1=0.768 8,ω2=0.231 2,ω3= 0。

步骤3 构建λ=0.5时误差平方和最小的GIOWA组合预测模型为

(16)

样本期内,式(16)组合预测误差平方和Q=6.086 3。

λ取不同值时，GIOWA组合预测值如表6所示。

表6 GIOWA算子取4种不同参数时对应的组合预测值Table 6 The combined predicted values of the GIOWA operator when four different parameters are taken

2.3 有效性评价

2.3.1 误差评价体系构建

通过查阅相关文献，选取误差平方和(SSE)、均方根误差(RMSE)、平均绝对误差(MAE)、平均相对误差(MAPE)和均方根相对误差(RMSRE)作为预测模型误差评价指标[14]，误差指标值越大说明模型预测效果越差，反之效果越好。并结合预测平均精度对各预测模型进行有效性评价[15]，结果见表7。

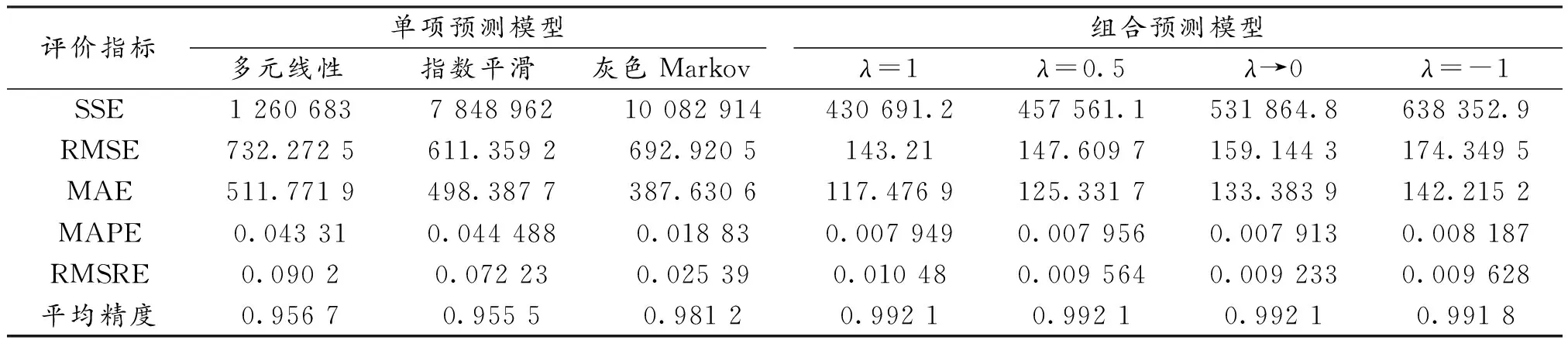
表7 模型预测效果评价体系Table 7 Model prediction effect evaluation system

由表7可以看出：当GIOWA算子取几种不同参数时，组合预测模型的误差平方和(SSE)、均方根误差(RMSE)、平均绝对误差(MAE)、平均相对误差(MAPE)和均方根相对误差(RMSRE)指标值均低于各项单项预测模型[14]，组合模型预测精度也高于单项预测模型。表明GIOWA组合预测模型相较于3种单项预测模型，预测精度更高，预测效果更优，预测结果也更接近实际值。

2.3.2 灵敏度分析

为更加直观地观察参数λ在[-1,1]间变动对GIOWA组合预测模型最优权系数、5种误差评价指标的影响，分别对参数λ进行灵敏度分析[16]，见图3和图4。

图3 λ变动对最优权系数的影响Fig.3 Influence of the variation of parameter λ on optimal weight coefficient

图4 λ变动对5种λ误差评价指标的影响Fig.4 Influence of the variation of parameter λ on the five λ error evaluation indexes

由图3可知，随着λ的增加，权系数ω1略微有所下降，ω2会随之增加，ω3近乎为0，λ变动对ω3影响甚微。

由图4可知，随着λ的增加，SSE下降趋势最为明显，除RMSRE外的4种误差评价指标都越来越小，说明预测值与实际值间误差越来越小。误差评价指标减小幅度较小，且除SSE外的4种误差评价指标都在0.3水平线下，说明组合预测模型预测结果更符合期望，效果更好。

2.4 GIOWA组合预测结果分析

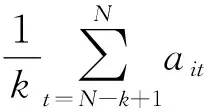
先拟合出3项单项预测模型2021—2025年的预测精度，再根据预测精度分别计算出λ取不同值时的GIOWA组合预测值，预测结果见表8。其中，应用多元线性回归模型对2021—2025年安徽省城镇居民人均可支配收入进行短期预测时，对于解释变量(IIFA，PCE，GDP，IS)2021—2025年的预测值可以通过判断解释变量IIFA，PCE，GDP与IS的时间序列趋势选择合适的时间序列模型进行预测。经过简单的趋势判断，对于PCE，IS，应用趋势外推法进行预测，对于IIFA，GDP，应用二次指数平滑预测法进行预测。

表8 2021—2025年安徽省城镇居民人均可支配收入预测结果Table 8 Forecast results of per capita disposable income of urban residents in Anhui Province from 2021 to 2025

从表8预测结果可以看出，2021—2025年安徽省城镇居民人均可支配收入将持续稳步增长。

3 结束语

首先应用多元线性回归模型、二次指数平滑预测模型和灰色Markov预测模型这3种单项预测模型分别对安徽省城镇居民人均可支配收入进行预测；然后引入GIOWA算子，将3种单项预测模型预测精度作为诱导变量，以误差平方和最小为计算准则，分别构建λ取不同值时的GIOWA组合预测模型以期提高预测精度、优化预测效果，再构建误差评价指标体系并对λ进行灵敏度分析；最后基于误差平方和及GIOWA算子组合模型预测2021—2025年安徽省城镇居民人均可支配收入。由结论可知：基于误差平方和及GIOWA算子的组合预测模型预测效果优于单项预测模型，且未来5年安徽省城镇居民人均可支配收入增长态势持续稳定。为实现城镇居民人均可支配收入持续稳定增加，驱动收入与经济同步增长，提高生活水平，需要政府坚持就业优先战略，推进积极就业政策以确保居民收入来源稳定，逐步健全完善社会保障制度，进而驱动经济可持续高质量发展。