一种基于HMM算法改进的语音识别系统

黄 清， 方木云

(安徽工业大学 计算机科学与技术学院，安徽 马鞍山 243000)

1 相关工作

隐马尔可夫模型[1](Hidden Markov Model，HMM)是一种统计信号模型，语音信号被分割成多个帧，将分割后的部门串起来，必须将这些部分串起来，这就需要用Markov链，而HMM模型就是通过Markov链演变形成的。HMM是体现语音信号特征的动态变化非常合适的一种模型，在识别语音的过程中，其识别精准度是非常高，现在HMM已成为公认的描述语音信号最为有效的统计模型，在如今的许多产品中有着较为广泛的应用。

国外2016年IBM团队[1]创造了7.0%的次错率新纪录，其解码部分采用的就是HMM模型，带有maxout激活的循环神经网络。微软2019年12月，利用了卷积以及LSTM(Long Short Term Memory)神经网络，开创了一个全新的声学训练，将字词错误率降到了近5.9%。国内2018年，科大讯飞提出了深度全序列卷积神经网络，并采用了大量的卷积直接对整段的语音信号进行建模处理，是为了获取语音信号中的信息。2019年阿里提出将LFR(Lancichinetti Fort-unato Radicchi benchmark)和DFSMN(Deep FSMN)算法进行融合[2]，语音识别错误率降低了25%，解码速度提升了近3倍多。它们虽然都使语音识别的精度有所提高，但是语音识别率还不够精确。基于持续时间状态的HMM模型，确保原本的精度上，更加提高识别精确度。

如果一个语音信号包括时间短暂且具有稳定特性的，就可以借用Markov链来叙述它，并且可以及时跟踪他们之间的状态变化的情况。而仅仅通过它得出其输出的最终序列状态，却看不见到它们之间的状态时间的改变情况和状态的分布信息，而HMM就是个双重随机过程，如图1所示。

图1 HMM模型状态图Fig.1 HMM model state diagram

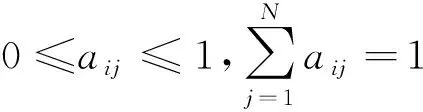
B是一个含有可见输出值几率的集合。B={bij(k)}，其中bij(k)是从状态位Si到状态为Sj转换过程中可见值xi为k的输出几率。为了便于形象化展示这个模型，HMM模型由马尔可夫链和随机过程组成的，如图2所示。

图2 HMM组成示意图Fig.2 Schematic diagram of HMM composition

2 隐马尔可夫模型的使用

在实际中要使用HMM模型来解决实际问题时，就需要解决3个问题：

(1) 对于一个HMM模型，如果已经有了观察值序列O=ο1,ο2,…,οT和模型M={A,B,π}，怎么样来计算由模型M产生出O的概率P(O|M)，在识别语音的过程中，需要计算得到P(O|M)这个概率，来寻找到与可观测值序列最高契合度的HMM模型。

(2) 在同样的观察值序列O=ο1,ο2,…,οT和模型M={A,B,π}，如何找到一种状态转移的顺序，有效得到与之对应的最佳状态序列。

(3) 怎样调整模型M={A,B,π}，使得P(O|M)最大。

2.1 计算输出概率P

Forward-Backward算法[3]是按输出观察值序列的时间来通过一个特定观察序列O=ο1，ο2，…，οT以及一个模型M={A,B,π}时进行计算，依靠模型M算出概率P(O|M)。为了有效求出P(O|M)，鲍姆等人提出前后向算法。设状态的起始值S1，状态的结束值是SN，以下为前后向算法：

(1) 前向算法。该算法凭借可见序列的检测值依次递进推出输出的计算概率。O=ο1，ο2，…，οT为可见信号的输出序列，P(O|M) 为模型M可见信号的输出序列O的概率，aij从Si到Sj变化状态的概率，bij(ot)从Si到Sj转变时输出状态ot的概率，αt(j) 为部分信号输出序列ο1,ο2,…,οt并且转换至Si的状态概率，称之为前向率，前向率αt(j)是依靠下面的公式推导计算得到：

初始化过程

α0(1)=1,α0(j)=0(j≠1)

递推过程

(t=1,2,…,T,i,j=1,2,…,N)

最终输出结果

P(O|M)=αT(N)

在运用递推前向算法过程中计算模型M={A,B,π}在输出观察符号序列为ο1,ο2,…,οT时的输出概率P(O|M)的具体步骤：

① 将每一个状态分配一个可变量数组αi(j)，在初始化进程时设置状态S1的最初变量数组α0(1)为1，状态的其余变量数组α0(j)为0。

② 根据t时间的可见信号οt的输出值情况，计算出αi(j)：

αt-1(2)a2jb2j(ot)+…+

αt-1(N)aNjbNj(ot)(j=1,2,…,N)

当状态Si到状态Sj没有转移时，aij=0。

③ 当符合t≠T这个条件时跳转到第二步，相反就进行第四步。

④ 把最新运算得到的变量数组中αT(N)的所以数值都提取出来，则P(O|M)=αT(N)

(2) 后向算法。设定βt(i)是后向率，从设Si为最初状态到设SN为终止状态过程中少许信号序列输出的概率为οt+1,οt+2,…,οT，则βt(i)可借助下列公式递推计算获得：

初始化过程

βT(N)=1，βT(j)=0，(j≠N)

递推过程

(t=T,T-1,…;i,j=1,2,…,N)

最终输出结果

根据定义的前后向概率，则有如下等式成立：

1≤t≤T-1

2.2 求状态转移序列

维特比算法[3]处理的是给定一个可见值序列O=ο1,ο2,…,οT和一个特定模型M={A,B,π}时，准确得到一个程度最合适的状态序列S=s1，s2，…，sT的问题。状态序列程度最合适的意思是指先让P(S,O|M)达到最大时得到的状态最准确序列。

初始化过程

递推过程

(t=1,2,…,T;i,j=1,2,…,N)

最终输出结果

③ 当符合t≠T这个条件时跳转到第二步，相反就进行第四步操作。

2.3 模型参数训练

在时间为t时Si转换至Sj时的稳态概率是γt(i,j)，则γt(i,j)的公式定义为

同时，对于信号字符序列O=ο1，ο2，…，οT，Markov链在时间为t时存在的Si状态的输出概率公式为

(1)

(2)

3 隐马尔可夫训练过程的改进和仿真比较

3.1 改进HMM的训练过程

传统的HMM描述状态持续时间具有较大的局限性，针对此问题，最直接的方法就是非参数方法，即在传统的HMM中，令状态转移矩阵A的对角线元素全为0(aii=0)则各状态没有自转移弧，再增添状态分布ρi(d)，设D是所有状态当中停留时间最长的，考虑状态持续时间的因素，HMM用Viterbi算法进行语音识别时，考虑状态持续时间的因素的HMM的输出概率为

3.2 仿真实验比较

实验采用的是0到9的阿拉伯数字[6]，因为与其他的语种相比，数字更加可以验证实验的结论。因为它们之间的发音有太多地方是相同的，并且识别数字的难易程度更高。为了比较传统的HMM算法与改进方法的训练效果，取了不同时间段的声音分为两组，这里设HMM的状态为4，HMM算法仿真中，先给定的一个HMM模型初始值如表1所示。

表1 HMM模型初始值Table 1 Initial values of HMM model

对传统HMM再进行对照训练，如表2所示的就是信号语音的训练过程，多次的反复训练之后，当其概率输出与它前面一个概率输出的差值与该概率输出值的比值大于HMM模型初始值4.5×10-6。训练之后的的HMM模型的参数如表3所示。

表2 传统HMM模型训练过程Table 2 Traditional HMM model training process

表3 传统HMM模型训练结果Table 3 Training results of traditional HMM model

两个办法各自的训练次数都为24，得到其对比仿真图如图3所示。图3仿真结果表明，改进后的HMM训练4次后，就可以达到较小的训练误差，并且训练收敛速度较快。而传统的HMM训练8次以上才能得到较小的训练误差，故HMM模型通过优化后的训练较之前下降得更快，更方便实现收敛，在一定意义上突出了改进办法的优越性。图4是训练后的识别结果。

图3 改进前后对HMM模型训练的性能影响Fig.3 The performance impact of HMM model training before and after the improvement

图4 HMM算法识别结果Fig.4 Recognition results of HMM algorithm

4 系统功能的实现

完成了各个部分的设计和编程后，就进行整个系统的效果检验[7]。本文所用的语音信号的都是预处理之后得出的语音信息，但首先需初始化客户端，与服务端建立连接。

(1) 语音识别功能。在语音识别模块中，先选取之前已经录制好的特定工作人员的语音，然后点击识别按钮(图5)，就会将录制好的语音信号很准确地翻译出来，并且可以判断这段录制好的语音文件是一个有效的波形文件，增加了语音识别系统的可信度[8]。

图5 语音识别功能图Fig.5 Diagram of speech recognition function

(2) 机器翻译功能。在将语音信号正确识别出来之后，该模块将语音指令转化为机器人指令。下图为一个语音指令成功转化[9]为机器人指令“停止工作”的图(图6)。

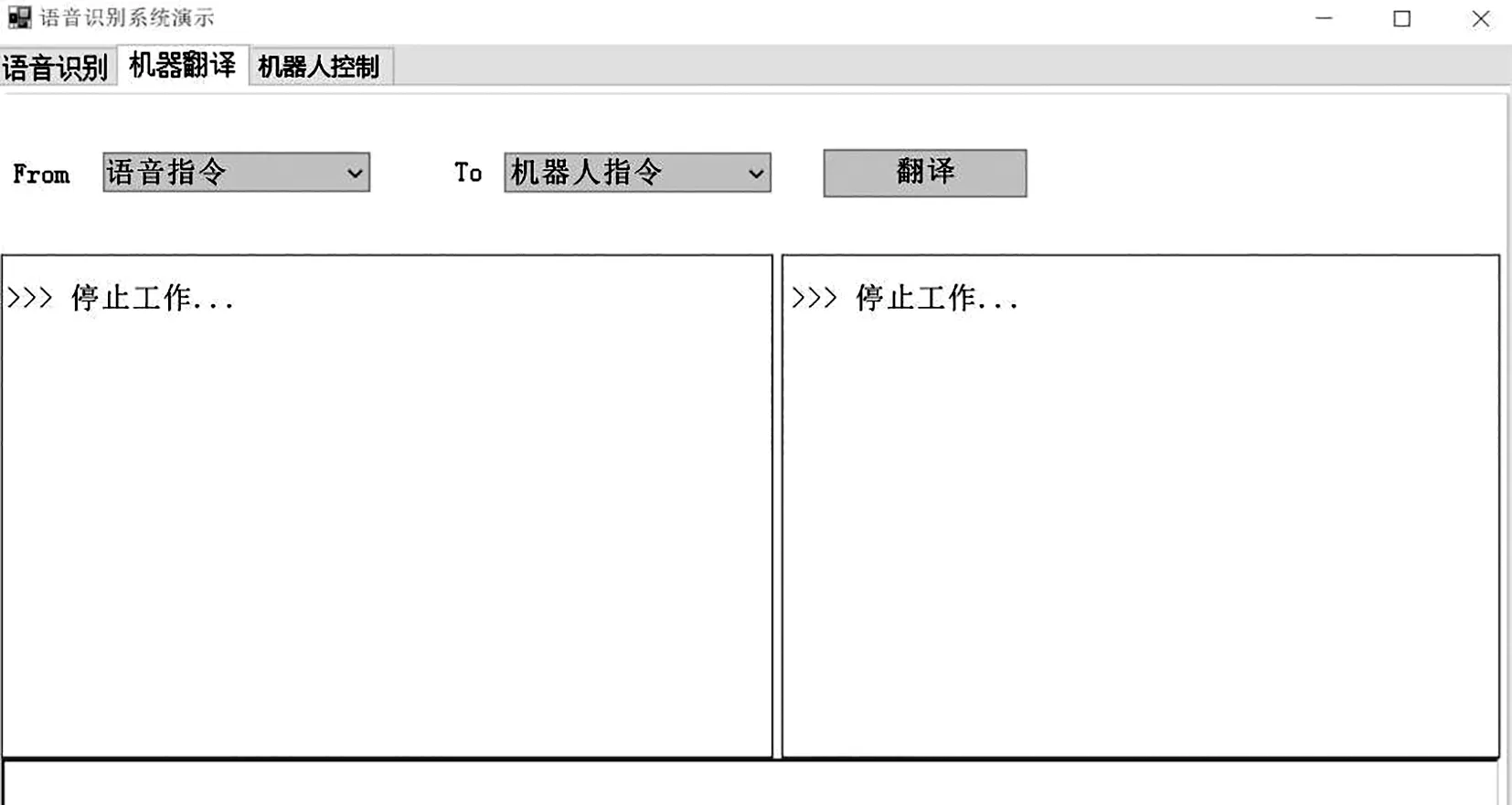
图6 机器翻译功能图Fig.6 Machine translation function diagram

(3) 机器人控制功能。该模块中有开始训练，手动控制，语音控制，结束功能，图7是点击开始训练，语音控制的效果图[10]。

图7 机器人控制功能图Fig.7 Robot control function diagram

5 结束语

主要介绍了HMM模型的概念，包括隐马尔可夫的定义和其3个问题的解决算法，其中重点介绍了HMM算法，最初的方式训练过程，基于信号语音的特点，对优化HMM模型的训练，再借助实验仿真的结果，证实了该方法具有优越性，训练改进后的HMM模型次数与时间均有所降低。并最终在HMM改进算法基础上实现了机器人语音识别系统。