基于SIR传染病模型的印度新冠疫情波及影响分析

丁黄艳， 铁禧玥

(重庆工商大学 数学与统计学院，重庆 400067)

0 引 言

新型冠状病毒肺炎(Corona Virus Disease，COVID-19)简称新冠肺炎，正威胁着全球居民的生命安全。如何快速控制疫情传播范围，切断传播链条，从而实现疫情感染人数清零，成为各国各地区民众普遍关心和亟待解决的问题。从2019年底疫情暴发至今，新冠病毒感染人数全球累计超过1亿6千万人，其中，死亡病例数已高达335万人，且与日俱增。随着防疫抗疫全球物资供给体系稳固和相关经验推广，市场信心和运行逐步从疫情恐慌的紧张情绪中恢复过来。但需要警惕的是，由于部分国家和地区防疫抗疫意识滑坡，新冠疫情呈现集聚反弹特征，严重威胁着全球疫情防控成果和公共卫生安全。

印度新冠疫情发展呈现出明显的“突然爆发—趋于稳定—迅猛反弹”特征。在经历了2020年第一阶段的疫情暴发后，通过全球抗疫资源援助和印度民众疫情防控努力，2021年初印度新冠每日新增病例数降至1万以下。面对疫情趋稳，当局者在疫情防控政策和执行力度上逐渐废弛，居民聚众屡见不鲜。经历短短3个月，印度新冠疫情伴随变异毒株迅猛反弹，每日新冠感染新增人数高达30万例以上，截至2021年5月30日，感染总人数高达2 800万，相对2021年初的1 000万人感染，64.2%属于反弹期感染病例，疫情近乎失控。针对印度疫情反弹及防控疏漏的前车之鉴，深化新冠疫情波及影响面的分析模拟，对于提高决策者和广大民众疫情防控意识，具有一定的现实意义。

1 文献综述

新冠肺炎是一种由冠状病毒引发的肺部炎症，目前该病毒引发的疾病已成为全球性重大公共卫生事件。该病发病5 d内传染性较强，致死率约为2%～4%，但这是一个非常早期的百分比，随着更多信息的获取，数据可能会改变。本文将应用传染病动力学模型对印度新冠疫情的波及影响进行分析。传染病动力模型最早于1760年为预防天花的研究中提出[1]；此后，Hamer建立了离散时间的荨麻疹传播模型[2]；17世纪，Kermack和Mckendrick[3]针对黑死病建立了动力学SIR仓室模型，全称为Susceptible-Infected-Recovered，即易感者(Susceptible)有α的概率被感染为感染者(Infected)，感染人群又有β的概率成为移除者(Recovered)，移除人群具有免疫性即被移出感染系统。SIR传染病动力学模型广泛应用于SRAS[4-5]、霍乱[6]等。文献[4]使用最基础的SIR模型进行拟合，文献[5]在传统SEIR传染病模型的基础上，对人群作了合理的分类，建立了控制前传播模型和控制后传播模型，通过合理估计、曲线拟合和概率平均的方法得到了各个参数。此后基于SIR模型发展并衍生出SEIR，SIRD，SIRV等传染病动力学模型[7-12]。

针对新冠肺炎疫情已有许多学者做出了相应的研究文献。文献[7]通过最传统的SIR模型对新冠疫情走势进行研究分析;文献[8]针对采取控制措施前SEIR模型和控制措施后SIR-YN模型，对控制后模型参数进行合理估计,并用MATLAB仿真预测新冠的发展走势，为疫情影响分析提供理论基础；文献[9]通过设定3种不同病毒潜伏期情景,依据国家及部分地区疫情数据,针对不同情景对模型参数进行仿真分析,对3种情形下的疫情拐点进行了预测。由于印度疫情暴发较为突然并且隔离措施较差，本身就可当作是一个密闭空间，所以使用传统SIR模型即可进行模拟。

还有部分学者基于基本再生数R0对新冠肺炎进行建模。通过文献[13]可知，有425例数据库病例描述了病例特征，估计了疾病倍增时间和基本再生数；文献[14]根据SEIR模型，通过2021年1月25日之前的发展得到新冠肺炎的基本再生数；还有些利用LSTM模型进行拟合预测[15-22]，如文献[15]，针对卷积积分对SEIR模型进行求解分析，虽求解十分严谨但缺乏参数确定的客观性；文献[21]基于自回归移动平均(ARIMA)模型和长短期记忆(LSTM)神经网络预测和分析舆情；文献[22]运用SEIR仓室模型以多重拟合确定参数，结合LSTM模型对疫情趋势进行综合预测，在参数估计方面更贴近临床实践。

可以看出，大多数文献在求解SIR模型参数时采取经验参数模式，缺乏一定的事实根基，故本文结合目标函数最优解思想进行相应改进。文献[4]和文献[23]曾使用龙格-库塔算法对2003年非典肺炎发展情况进行预测和分析，效果较好且暂时还未有学者使用该方法与SIR模型相结合对印度疫情进行及时的预测及分析。为了解印度变种毒株的威力以及对全人类的危害，研究以印度新冠疫情为例，运用SIR动力学模型进行疫情预测，主要因为印度疫情反弹特征在后疫情时期具有一定的代表性。

研究通过建立目标函数求解参数最优解，并使用龙格-库塔算法求解微分方程的数值解，并对此方法进行改进。首先根据印度疫情数据进行拟合并预测疫情走势，然后结合印度当下实情来判断印度是否会持续暴发疫情、将会在何时出现拐点等印度疫情波及影响，最后结合印度当下疫苗情况建立SIR模型，判断印度以现有能力接种疫苗，建立有效群体免疫屏障时的疫苗接种率，针对加入疫苗有效保护率因素，加大疫苗供应量等情况进行讨论，并以此提出相应防治对策。

2 SIR传染病动力学模型构建

2.1 模型构建

模型假设在封闭系统内，故该系统的总人数N满足恒等式N=S+I+R；S为易感者人数；I/N为感染者在模型中所占比例,根据伯努利(Bernoulli)大数据定律[24]，可以将I/N作为遇见感染者的概率，则S(t)I(t)/N(t)，即t时刻易感者遇见感染者的人数；α为感染率,故αS(t)I(t)/N(t)为t时刻易感者被感染的人数；同理βI(t)为t时刻感染者被移除的人数。传播流程如图1所示。

图1 SIR模型传播示意图Fig.1 Transmission diagram of SIR model

首先对模型进行如下假设：假设模型中总人数N不变；假设感染率及移除率为常数；假设被隔离者与外界隔离，不具有传染性；假设感染者中康复人群康复后会产生抗体，不会被再次感染；假设感染者中死亡人群被移除模型，不具有感染性。接下来进行变量符号说明(表1)。

表1 符号说明Table 1 Symbol description

据模型分析可以列出SIR模型常微分方程式：

(1)

可以发现易感者人数St为单调递减函数，移除者Rt为单调递增函数，当感染者It的人数开始下降时即为疫情出现拐点，此时满足如下方程：

由此可以推出拐点出现在St=Nβ/α处，则可以发现α越小β越大即Nβ/α越大疫情消退早。

2.2 数据来源

印度2021-03-31—05-16的疫情数据来自约翰·霍普金斯大学系统科学与工程中心(CSSE)提供的COVID-19数据存储库；印度2021-03-31—05-18疫苗接种数来自Kaggle数据集COVID-19 World Vaccination。

3 基于印度疫情的SIR模型应用

3.1 龙格-库塔算法结合目标函数求解最优参数

截至2021年5月22日，印度累计确诊病例突破2 600万例，但国际社会对印度官方提供的疫情信息表示怀疑，印度新德里疾病动态、经济和政策中心主任纳斯米瑞安表示“根据去年的估计，30个感染者中只有1个被检测出来”。鉴于印度数据的真实性问题，对模型中总人口数进行相应比例缩小，设置印度模型总人口数N=3 000万，通过印度近一个月的疫情数据应用SIR模型预测。

接下来使用Matlab中的ode45函数求解上述微分方程数值解，为求微分方程中α，β的最优解，通过确定α，β的范围并建立真实值与预测值之间的残差平方和方程作为目标函数来加强条件，对该约束优化问题求解，使得目标函数值最小的α，β即为方程的最优数值解。

为确定α，β的范围将式(1)递推得到如下迭代式(2)：

(2)

由迭代方程可见：St-St-1和St-1It-1/N以及Rt-Rt-1和It-1满足线性关系，于是对上述变量进行线性回归拟合(图2、图3)，得到斜率即未知参数α，β的范围为α∈[0.180 7,0.458 7]，β∈[0.053 3,0.097 1] 。

图2 参数α范围预测 Fig.2 Prediction of the range of parameter α

图3 参数β范围预测Fig.3 Prediction of the range of parameter β

建立目标函数作为约束条件：

r2=(Sact-Sp)2+(Iact-Ip)2+(Ract-Rp)2

运用Matlab中fmincom函数求得未知参数最优解为α=0.272 5，β=0.071 2。将最优解带入迭代方程计算预测数据，并对未来100 d进行预测，将真实数据与拟合数据进行叠合，如图4所示。

图4 印度疫情数据预测Fig.4 Prediction of epidemic data in India

通过图4可以看出:总体拟合效果较好，印度疫情的拐点将出现在2021年5月7日到5月9日期间，此后模型中现存感染者人数It将开始下降，说明累计确诊人数将达到饱和，新增确诊人数也会开始下降，再通过预测未来200 d的数据绘制模拟累计确诊人数和新增确诊人数。

3.2 推导分析累计确诊和新增确诊人数

模型中预测出感染者It的曲线为现存感染者，即现存确诊人数的走势图，据此，根据累计确诊人数=It+Rt-1和新增确诊人数=当期累计确诊人数-上期累计确诊人数，推导得到印度未来估计累计确诊人数和新增确诊人数数据，绘制折线图5和图6。

图5 预测印度累计确诊人数Fig.5 Prediction of the cumulative number of confirmed cases in India

通过图5和图6对单条曲线进行观察，尽管总体拟合效果较好，但是实际确诊和每日新增确诊人数略高于预测值。追溯其原因，主要是由于连续每日超过30万人次的确诊病例，使得印度脆弱的医疗系统濒临崩溃，各种医疗用品严重短缺，氧气供应不足，印度医疗系统无法应对病人的增长速度，无法收治这么多病人，导致很多感染者在家里接受治疗，病毒在各个社区快速传播形成恶性循环。在这样的循环里，患者得不到良好的隔离，使得感染率α增大，医疗系统的崩溃会使得移除率β降低，这两方面的变化在图5和图6中表现为确诊人数和每日新增高于预测值。

由于新冠病毒变种的不确定性，预测也只是在新冠病毒变种速度可控范围内进行，如果病毒进入不可控状态，则该模型将不适用于此时的印度，并且假设不出现近期爆发的毛霉菌病的交叉感染所导致的染病及死亡。

4 建立加入疫苗因素的SIR模型讨论防治对策

4.1 群体免疫屏障

要使疫情更快速走向末尾，或者说更快地复工复产，必须更快速地构建“群体免疫屏障”，即注射疫苗。此次新型冠状病毒是一种以前从未被发现的冠状病毒新毒株，因此在疫情暴发时可以不考虑疫苗因素，但在当今科学技术下，随着病毒的蔓延和时间的推移疫苗一定会出现，加入疫苗因素会使模型的预测更为准确且更具有实际意义。在模型中加入疫苗因素，考虑它对之后疫情走向的影响，并采用近期疫情严重的印度作为研究对其进行预测和拟合。

4.2 模型建立

通过加入疫苗因素γS来建立群体免疫屏障，假设疫苗供给量每天一定，为γS=k，改进后的方程如下所示：

(3)

对式(3)进行迭代得到如下递推方程式(4)：

(4)

4.3 印度疫苗接种情况

根据印度近50 d疫苗接种数据,利用Rstudio绘制散点图(图7)，并进行95%置信区间的曲线拟合。

图7 印度2021-04-01—05-18疫苗接种情况Fig.7 2021-04-01—05-18 vaccination status in India

据图7所示，通过拟合曲线趋势可以大致发现印度未来每日疫苗接种数量≥15万剂。美国对疫苗原材料出口的限制和印度疫情的严峻形势导致印度疫苗产量下降，出现了疫苗紧缺的情况。可以看出印度每天平均注射疫苗剂量已经从4月初的360万剂下降到现在的100多万剂，目前印度已经禁止疫苗的出口和捐赠，将疫苗全部用于满足本国的需求。印度政府表示从2021年5月1日到6月15日，向各邦免费提供Covaxin和Covisshield两种疫苗共计5 862.9万剂，到2021年6月底各邦还可以直接从制造商购买4 875.5万剂疫苗，平均下来每日接种剂量也不超过150万剂，所以预计近期印度疫苗每日接种人数在100万剂到200万剂。100万到200万这个范围对应的是全体印度13亿人口，由于本模型总人口设置为3 000万，同比例减少，即可得未来日接种剂量范围在2.3万到4.6万剂，因此选择3万剂疫苗开始试验。

4.4 疫苗接种率的灵敏度分析

由于前半月每日超过30万例的新增确诊击穿了印度的医疗系统，新冠病毒的治疗方法没有很大突破的空间，根据上一节对印度近期接种疫苗数的观察，建立关于疫苗接种数和感染率的相关性模型。

Pd(t)为当日疫苗接种人数占总人数N的比重，假设感染率α下降比率满足：

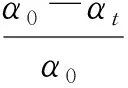
(5)

以3万支疫苗为基础，当每日给印度接种3万剂疫苗，即k=30 000时，计算SIR模型参数值α最优解为0.250 2，故α0=0.272 5，αt=0.250 2，Pd(t)=k/N=3万/3 000万=0.1%，代入式(5)求得δ≈82。得到模型具体表达式(6)：

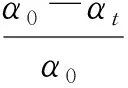
(6)

根据式(6)，适当增加每日接种疫苗数进行灵敏度分析(图8)：当每日给印度接种3万支疫苗，即k=30 000，病毒感染率下降10%，即此时感染率α=0.250 2；当每日给印度接种6万支疫苗，即k=60 000，病毒感染率大致下降16.4%，即此时感染率α≈0.227 8；当每日给印度接种9万支疫苗，即k=90 000，病毒感染率大致下降24.6%，即此时感染率α≈0.205 5；当每日给印度接种15万支疫苗，即k=150 000，病毒感染率大致下降41%，即此时感染率α≈0.160 8。

图8 疫苗接种率灵敏度分析图Fig.8 Analysis chart of the sensitivity of vaccination rate

当每日接种15万支疫苗时，疫情已经被控制，感染人数无明显峰度变化，较为平缓，到第150天时，几乎没有现存感染者，此时已经累计接种了15万×150天=2 250万支疫苗。该印度SIR模型中假设的总人数N=3 000万，即意味着当疫苗覆盖率大约为2 250万/3 000万=75%时，疫情可以被有效控制。

4.5 建立群体免疫屏障的有效疫苗覆盖率

当基本传染数R0<1时，传染病会消失；当R0>1时，传染病将爆发变为流行病。因此，需要注射疫苗来增强免疫力，进而起到减小R0的作用，直至传染病消失。假设疫苗覆盖率为Pvac，当传染病消失时，有公式：(1-Pvac)×R0<1。

2021年，一个中外合作团队在medRxiv网站上发表预印《2019年新型冠状病毒在中国暴发的传染病学和临床特征》，研究认为：不考虑疫苗有效保护率情况下，新冠肺炎病死率为3.06%，远低于严重急性呼吸综合征(SARS)，但传染性与SARS相当，基本传染数R0达到3.77。新冠疫情的R0大约为3.77，因此可以得出新冠疫情的疫苗覆盖率为Pvac>73.47%,与预测结果相似。考虑疫苗有效保护率的情况下，目前国家公布的新冠疫苗有效保护率为79.34%，所以印度大概需要92.6%的人注射疫苗，但考虑到印度病毒变种的情况，导致疫苗有效保护率可能会有一定程度的下降，疫苗接种覆盖率需要高达95%才能建立起群体免疫屏障。因此印度政府应号召大家尽快接种疫苗，在有资源及能力的情况下，尽快建立起群体免疫屏障才是共同抗疫的团结表现。

5 结 论

针对近期印度出现新冠病毒疫情第二次爆发，通过SIR传染病模型研究新冠肺炎对印度的影响，预测疫情拐点将出现在2021年5月8日左右，虽在未来100 d内将持续出现新增病例，但疫情现期已经有消退趋势。结合印度真实的医疗情况，考虑病毒的变异情况未知，若想短期内印度疫情能得到较好地控制，需要尽快建立群体免疫屏障。

研制出疫苗并上市后，α和β便会受到疫苗因素γS=k的影响，因此在模型中加入疫苗因素进行模拟。改进后的模型预测表明：要使印度疫情得到有效控制，疫苗覆盖率大致为75%；考虑疫苗保护率因素的影响，会导致印度疫苗覆盖率继续增大，甚至需要95%以上群众接种才可以建立有效群体免疫屏障；最后通过拟合新冠病毒的基本传染数计算出疫苗保护率大致为73.47%，也可以对上述结论进行验证。