逆正向蒙特卡罗方法及应用

施国栋

(上海财经大学金融学院,上海 200433)

0 引言

蒙特卡罗方法在确定性问题、粒子运输、大气环境模拟、数理统计学、金融经济学和科学实验模拟等领域有着广泛应用。蒙特卡罗方法计算结果精确,当所研究的问题没有解析解时,蒙特卡罗方法的结果往往可以作为基准解[1]。蒙特卡罗方法计算比较灵活,在解决介质的辐射特性问题时,根据光路可逆性原理,可以分别使用正向或逆向蒙特卡罗方法模拟光线的传播与能量分配[2,3]。然而对于一些不可逆的问题,即需要根据事物当前的状态值计算下一个状态,则不可以用逆向蒙特卡罗方法计算,因此需要对传统的单向蒙特卡罗方法进行改进。

目前考虑偏振效应的辐射传输研究中,Lau与Watson[4]导出了梯度折射率介质中偏振光辐射传输方程。Zhao等[5,6]完整地推导了梯度折射率介质中矢量辐射传输方程。Ben等[7]采用正向蒙特卡罗法求解了矢量辐射传输问题,提出了一种模拟梯度介质中偏振辐射传输的方法。

在非均匀折射率介质中光线轨迹通常是弯曲的,光线在传输过程中会出现会聚或发散,即使在透明介质中,光线传播也会引起偏振椭圆旋转,从而引起能量的重新分配。椭圆偏振的传输是由Rytov场矢量旋转法描述[8],所以光的偏振状态在梯度折射率介质中会不断变化,并影响下一时刻的结果,这使得对光线反向跟踪变得不可能。反向蒙特卡罗法可以从某个特定角度出发对光线进行跟踪,从而极大减少了跟踪光束的数量[9-11]。考虑偏振状态的辐射传输问题,如果可以通过反向蒙特卡罗法求解,可以有效减少计算时间和避免角度离散,从而获得更高精度的结果。

近几十年来,一些学者试图采用反向计算方法来解决矢量辐射传输的问题[10,12-14]。但是光子的散射方向受偏振状态影响较大,这些近似方法可能无法提供准确的结果[15]。为了解决这类复杂问题,本文发展了更为灵活的逆正向蒙特卡罗法(RFMC),打破了传统单向蒙特卡罗方法计算的连贯性,模拟计算了一维梯度折射率介质自身的Stokes矢量。

1 逆正向蒙特卡罗法

1.1 物理模型

图1为一维梯度折射率半透明介质的多层模型,假设介质为无限大的平板,厚度为L,折射率的分布沿着z轴方向,下表面处折射率为n0,上表面处折射率为nL,这种模型与大气层的梯度折射率分布类似。介质被假定为吸收、发射、散射或非散射性介质,吸收系数为κa,介质的温度场为等温分布,灰色半透明介质和纯镜面反射边界符合Snell定律和Fresnel定律。研究的重点为梯度折射率介质模型以及上下表面的表观发射率。

图1 一维梯度折射率半透明介质多层模型Fig.1 Multilayer model of one-dimensional gradient refractive index translucent media

光线在一维梯度折射率介质中轨迹的跟踪可以使用简单的多层近似方法[16],每个子层的折射率近似等于该子层中心点折射率。基于该假设,每一层都有固定的折射率,光线在每个子层中沿直线传播,两层之间虚拟的界面被假定为折射或全反射界面[17]。利用蒙特卡罗方法对光线模拟时,将光线跟踪的过程分成发射、传播、散射、反射、吸收等一系列子过程。

1.2 Stokes矢量计算子过程

光线在非散射一维梯度折射率介质中的轨迹为一个平面,从文献[4,5]可以得到

式中S为Stokes参数,S=(I,Q,U,V)[18],I是辐射强度,Q是垂直和水平方向线偏振强度,U是±45°方向上偏振强度,V是圆偏振强度;s为光线轨迹弧长;n为折射率。

光线在经过介质反射、折射和散射后的Stokes矢量为Sref、Srefr和Ss,其计算公式分别为

式中Si是入射Stokes矢量,R(θi)为反射矩阵,T(θi)为折射矩阵,θi为入射角,M(Θ)为单次散射的Mueller矩阵,Θ为散射角,L表示沿着光线传播方向的旋转矩阵,i1、i2是图2中旋转的角度。下面分别列出R(θi)、T(θi)和M(Θ)的计算方法。

式(2)中的反射矩阵R(θi)可以表示为[19-21]

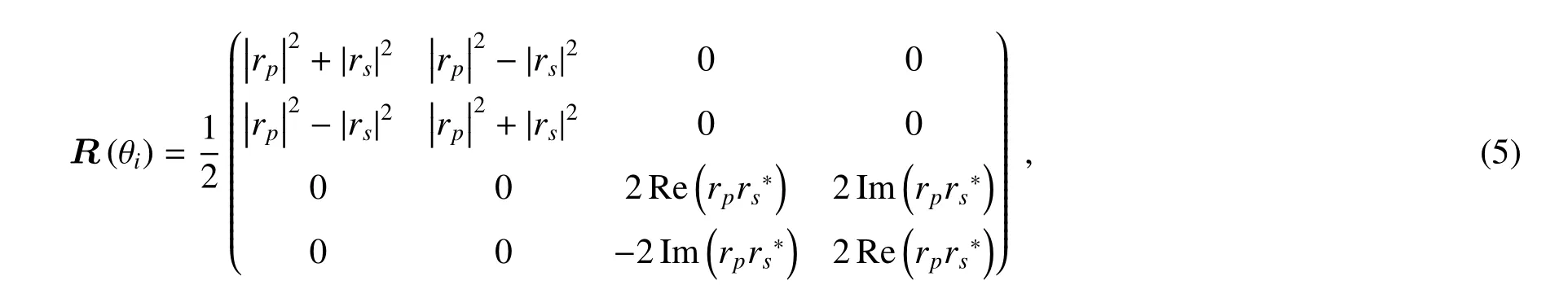
式中θi为入射角,rp和rs分别表示平行和垂直偏振的振幅反射率,Re()和Im()分别表示复数的实部和虚部,*表示共轭复数。rp和rs分别用菲涅耳方程来计算,即

式中ni和nt分别为入射边的折射率和折射边的折射率。

式(3)中的折射矩阵T(θi)可以表示为

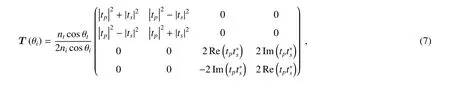
式中θt为折射角,tp和ts分别为p和s偏振的透射系数,其计算公式分别为

矢量辐射传输中散射比较复杂,由Van de Hulst定义[22],M(Θ)的形式为

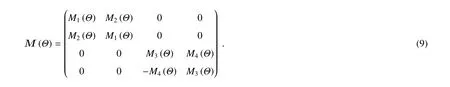
图2为入射光与散射光线的几何关系。Si(θ1,φ1)和Ss(θ2,φ2)分别是光线散射前后的方向,Θ为散射角,即入射和散射方向之间的夹角。矩阵L表示沿着光线传播方向顺时针旋转的旋转矩阵,其表达式为[23]

式中Φ(等于i1或者i2)是图中旋转的角度。

相关的一些角度可以由图中几何关系得到。图2中入射Stokes矢量Si和z轴确定平面aoz,散射后的Stokes矢量Ss和z轴确定平面boz,Si和Ss确定了散射平面。i1是平面aoz与散射平面的夹角,i1∈[0,2π),服从均匀概率分布,i2是平面boz与散射平面旋转的夹角。在不考虑矢量辐射传输的标量模拟计算中,光线的散射角通常采用反向插值方法计算[24],而在考虑矢量辐射传输时,可采用拒绝法确定光线的散射方向。

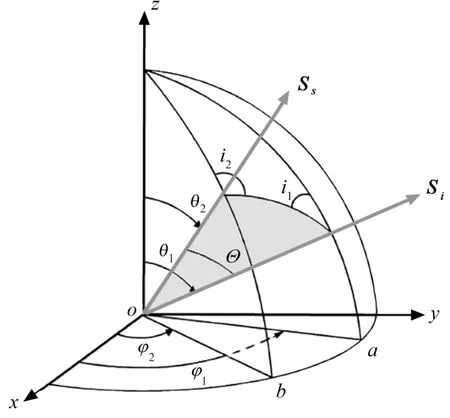
图2 入射光与散射光的几何关系Fig.2 Geometric relation of incident light and scattered light

1.3 拒绝法确定散射方向

拒绝法是一种产生给定分布函数的方法。在图2中已知入射光线Si(θ1,φ1)的天顶角和圆周角,散射方向i1和Θ通过拒绝法来确定[25,26],其他角度i2、θ2和φ2可以用空间余弦定理来确定[27]。

采用拒绝法确定散射方向i1和Θ的步骤为:

1)散射角Θ和i1在局部坐标系中定义,其计算公式分别为

式中RΘ和Rφ是均匀分布的随机数,随机范围在[0,1]区间。

2)计算Is′和Is,max′。

在散射平面定义Stokes矢量,散射后Stokes矢量可以表示为

将式(12)展开,得到

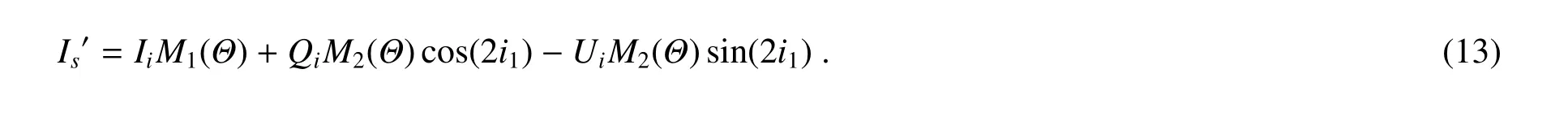
将步骤1)中生成的散射角Θ和i1代入式(12),得到Ss′中I部分的分量,即为Is′。

根据三角函数公式将式(13)变形为

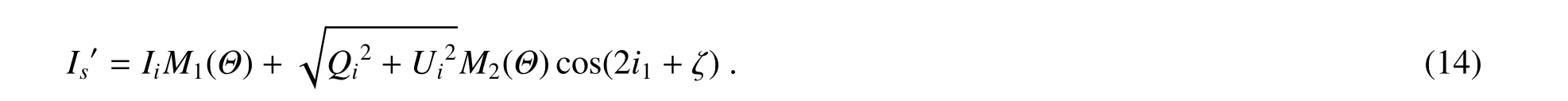
得到式(14)中散射角Θ对应的最大值Is,max′[7]。

3)采用拒绝法来判断生成的散射方向Θ和i1是否有效。

比较步骤2)中的Is′和ζIs′,max,其中ζ是[0,1]区间内均匀分布的随机数。如果Is′≥ζIs′,max,那么步骤1)中生成的散射方向是有效的;反之则步骤1)中生成的散射方向是无效的,重复步骤1)直到生成新的散射方向被接受。

1.4 逆正向蒙特卡罗法计算流程

Stokes矢量的第一部分分量I表示光子所携带的能量,而其他部分(Q,U,V)表示光线的偏振状态。采用蒙特卡罗法模拟时,为了确保能量守恒,需要对Stokes矢量进行归一化处理,即在光线轨迹上,Stokes矢量中第一部分I保持为1。Stokes矢量的归一化公式为

在一维非散射梯度折射率介质中光线轨迹是一个平面,根据式(1)和式(15),光线在介质中传播的子过程中Stokes矢量虽然不断变化,但是在归一化后其S′值不变,即在一维非散射梯度折射率介质的子层传播过程中Stokes矢量不发生变化。

但不能使用传统标量反向蒙特卡罗法,主要原因是:

1)在矢量辐射传输问题中,计算反射系数的公式与标量辐射传输问题中不同。当光线从介质1入射到介质2时,考虑偏振的反射率ρf为

式中θ为入射角;ρ是标量方法中的反射率;Q是入射Stokes矢量Si中的第二部分分量;rp和rs分别是平行和垂直偏振的振幅反射率,采用菲涅耳公式(6)来计算。虽然Q分量最终引起的反射率变化不是很大,但是考虑偏振的反射率公式和标量方法的反射率公式不一样。

2)在考虑偏振时确定散射方向与标量方法不同。考虑偏振时散射方向Θ和i1是否有效,可以使用拒绝法来判断。在式(13)中,考虑偏振时的散射方向与Ii、Qi、Ui、M1(Θ)、M2(Θ)这些量都有关;而只考虑标量问题时散射方向的确定与散射相函数有关。在各向异性散射的问题中,Qi、Ui不等于0,因此各向异性散射介质考虑散射偏振问题的结果与只计算标量问题的结果不同。

根据以上两点,不能直接使用标量反向蒙特卡罗法。因此提出了逆正向蒙特卡罗法,即在光线跟踪时采用逆向跟踪方法,通过反向光线跟踪找到光线在介质内的终点,然后在Stokes矢量计算时则采用正向计算。在正向Stokes矢量计算时式(2)不变,因为入射角和反射角相等;式(3)原折射角变为入射角;i1和i2相互交换,坐标旋转方向由顺时针方向变化为逆时针方向。式(4)则变为

逆正向蒙特卡罗法的理论框架应遵循“正向”蒙特卡罗法,逆向光线跟踪的过程只是在介质中找到光的终点,然后该终点变成下一步正向计算时光线的起点。

图3为逆正向蒙特卡罗法的光线跟踪示意图。图中黑色实线为光线反向跟踪的轨迹,灰色实线是光线正向Stokes矢量计算过程。利用逆正向蒙特卡罗法求解考虑偏振状态的表观发射率的算法,可以概括为如下步骤:

1)从反向跟踪的起点开始,模拟光线的总数量为N,假设光线全部进入介质内而不发生反射。跟踪光线并记录各子过程的相关信息,如入射方向、折射方向、折射率、散射方向等,以用于正向Stokes矢量计算。

2)每一束模拟光线在被散射和吸收之前所传播的距离为

式中κ为介质的吸收系数;Rs∈[0,1],是一个均匀分布的随机数。

3)光线在传播过程中如果发生散射,散射角Θ和i1通过式(11)确定,并假设所有生成散射方向都是有效的,继续跟踪散射后的光线。

4)图3中光线(黑色实线)在传播过程中遇到边界时,不考虑光线折射透过介质,即假设上下界面为镜面反射,继续跟踪直到光线被介质所吸收。

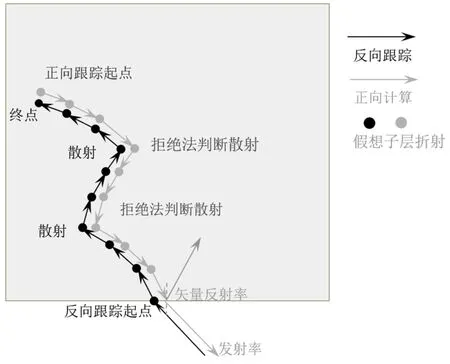
图3 逆正向蒙特卡罗法光线跟踪轨迹示意图Fig.3 Ray tracing track diagram of reverse forward Monte Carlo method

以上四个步骤是光线的“特殊”反向跟踪过程,下面是正向Stokes矢量计算过程。

5)在逆向光线跟踪完成后,根据光路的可逆性,光线可以沿原来路径返回。光线的Stokes矢量计算时使用之前已存储的数据,而无需重复跟踪光线。

6)在正向计算的光线到达界面处,使用矢量辐射传输问题的反射率公式(16)判断光线是透射还是反射,如果在表面透射则停止跟踪。同样,当光线到达散射的位置时,根据拒绝法来判断之前存储的散射方向是否有效,如果无效则停止这束光线的跟踪,并记录被拒绝的总次数。最后在模拟光线的总数量中减去拒绝法所拒绝的总次数,这相当于在标准的拒绝法中重新生成随机数的过程。

7)最终可以沿着原来入射方向射出介质光线的比例就是表观发射率,表观Stokes矢量S(θ,φ)公式为

式中i为图1中的i子层;K为介质子层数;Ib(Ti)是i子层温度的黑体辐射强度;Ni→s1为从i子层发射的光线可以沿着介质表面的(θ,φ)方向发射出去的总数;Sm(θ,φ)是第m根光线归一化的Stokes矢量;N为光线追踪的总数;Nrject为各向异性散射介质中被拒绝法拒绝的总次数,对于非散射问题和各向同性散射类问题,Nrject=0。

2 一维梯度折射率介质矢量辐射传输

2.1 非散射性介质

设模型的介质折射率分布为n(z)=n0+(nL-n0)z/L,z为折射率变化方向,上下两个边界处的折射率分别为n0和nL,n0=1.2,nL=1.8,厚度L=0.1。该模型是一个无限大平行吸收发射的平板,为非散射灰色半透明介质,其边界被认为是纯菲涅耳反射。介质的吸收系数κa=10m-1,光线的初始Stokes矢量为S0=(1,0,0,0)T。研究的重点是介质上下表面某点的Stokes矢量,并与文献[28]中的标量方法结果进行了对比。

图4是采用逆正向蒙特卡罗法计算上表面处I、Q两个分量的结果,而U和V分量等于零没有在图中绘制,其计算条件为n(z)=1.2+0.6z/L,L=0.1,κa=10m-1,S0=(1,0,0,0)T。反向跟踪模拟光线的总数量为106,当模型被划分为100层和200层时,计算结果十分接近,而10、20、50层之间的偏差较大。为了保证其结果的精度,本研究采用将介质划分为200个子层的近似方案进行计算。

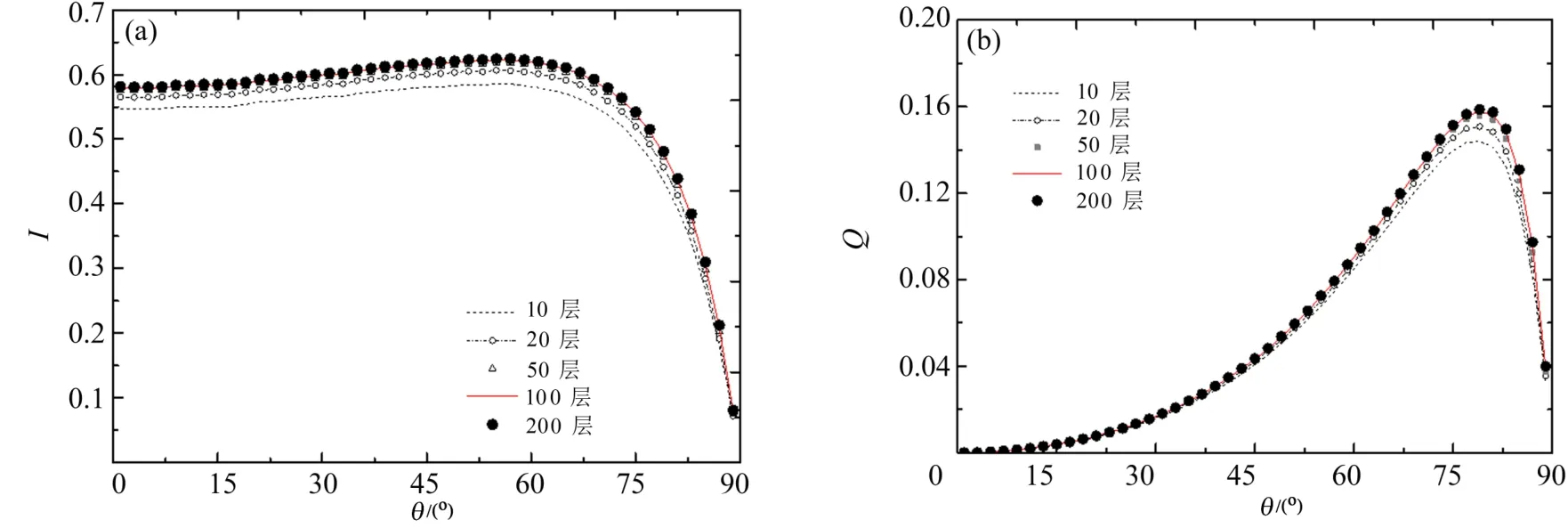
图4 不同子层数量时上表面某点的Stokes矢量。(a)I分量;(b)Q分量Fig.4 Stokes vector of a point on the upper surface with different sublayers.(a)I component;(b)Q component

εp和εs分别是表观定向平行发射率和表观定向垂直发射率,其与Stokes矢量的换算关系为

式中Ip是P极化波的辐射强度,Ib是黑体辐射强度,Is是S极化波的辐射强度。

图5是采用逆正向蒙特卡罗法所计算的等温条件下介质上表面某点的方向发射率与文献[28]结果的对比,计算条件为n(z)=1.2+0.6z/L,L=0.1,κa=10m-1,S0=(1,0,0,0)T。采用逆正向蒙特卡罗法所得到的结果和文献[28]标量方法结果一致,其表观定向平行发射率εp相对于表观定向垂直发射率εs要大一些。对于均匀分布的等温介质,其上下表面的发射特性一致。而对于梯度折射率分布介质,介质上下表面的发射率则存在明显的区别,梯度折射率介质与均匀折射率介质表现出不一样的辐射特性。

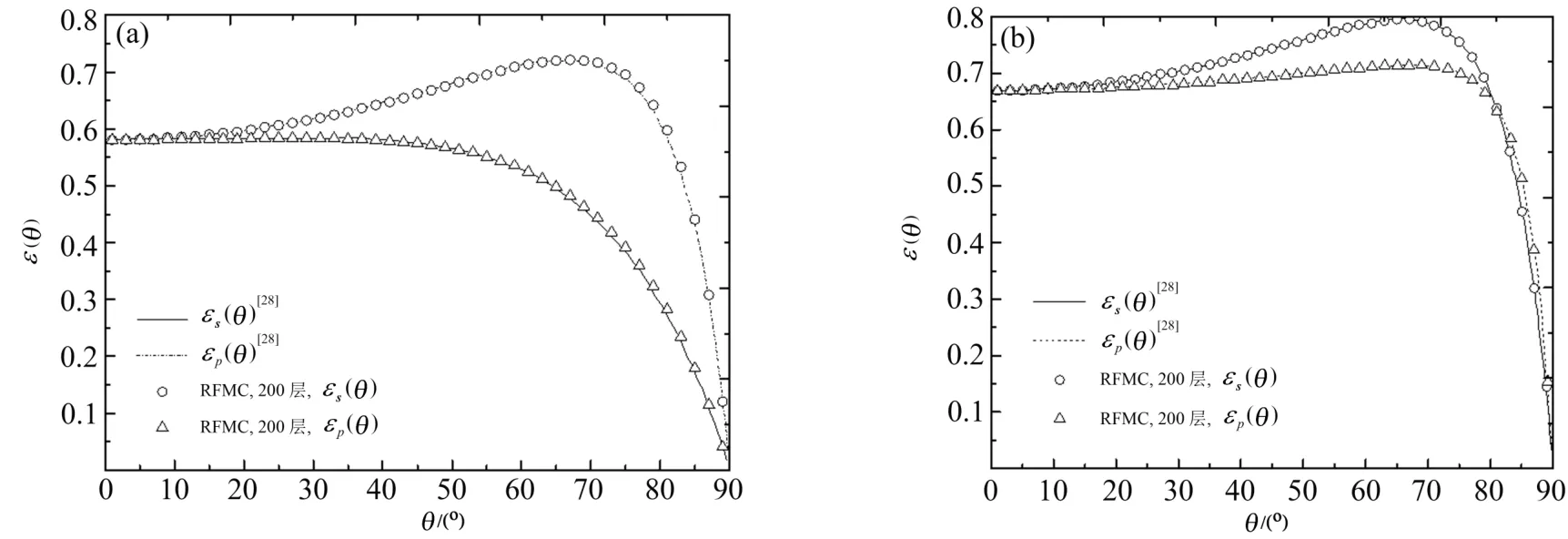
图5 介质上下表面某点的发射率对比结果。(a)I分量;(b)Q分量Fig.5 Emissivity comparison of a point on the upper and lower surface of a medium.(a)I component;(b)Q component

图6 为不同光学厚度介质τ在上表面的Stokes矢量,计算条件为n(z)=1.2+0.6z/L,L=0.1,κa=10m-1,S0=(1,0,0,0)T,200子层,模拟光线的总数量为106。随着光学厚度的减小,在大多数角度中更多的光线会直接穿过介质,使得I和Q部分的分量随着光学厚度变小而显著减少。但当光学厚度在0.7、角度在75°以上时,I和Q的分量没有减小。此时光线厚度虽然有所减少,但是在入射角度较大时,界面反射概率增加和全发射的发生使得光线继续在介质中传播,并产生线性偏振。

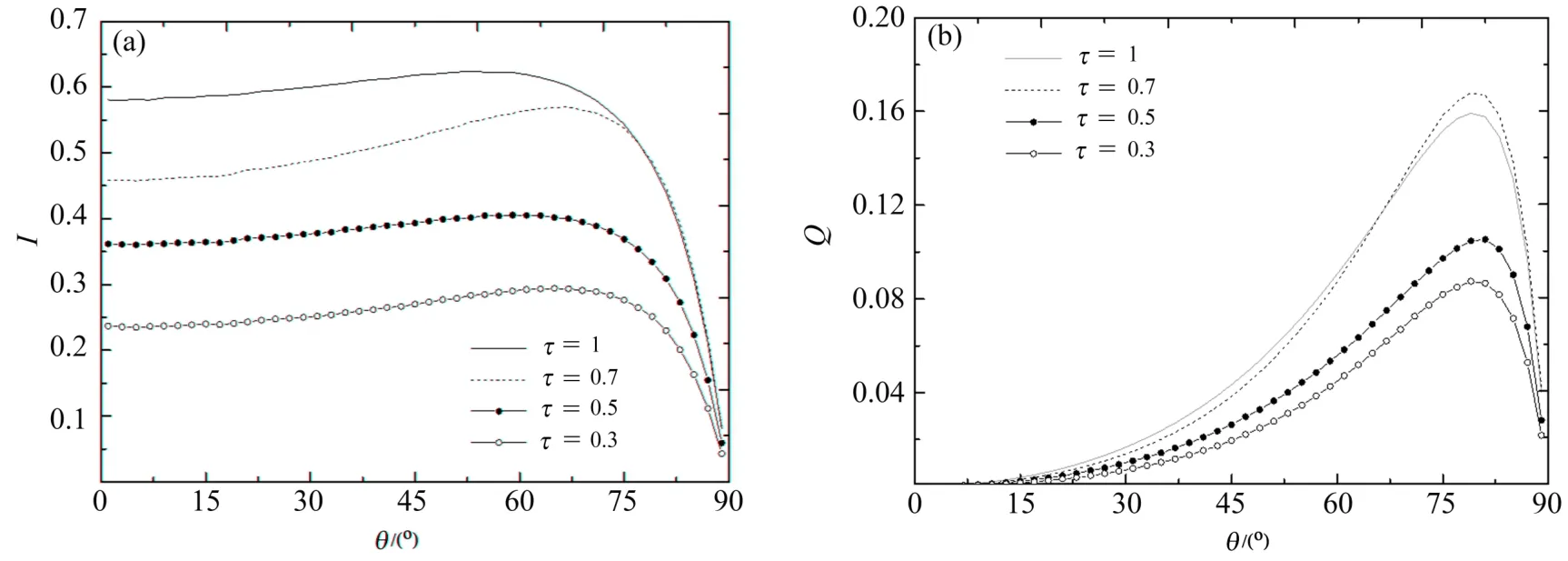
图6 不同光学厚度介质上表面的Stokes矢量。(a)I分量;(b)Q分量Fig.6 Stokes vectors of upper surfaces on media with different optical thickness.(a)I component;(b)Q component

2.2 各向异性散射性介质

当介质散射类型为瑞利散射时,散射光的强度和入射光波长的四次方成反比,其散射相矩阵M(Θ)为

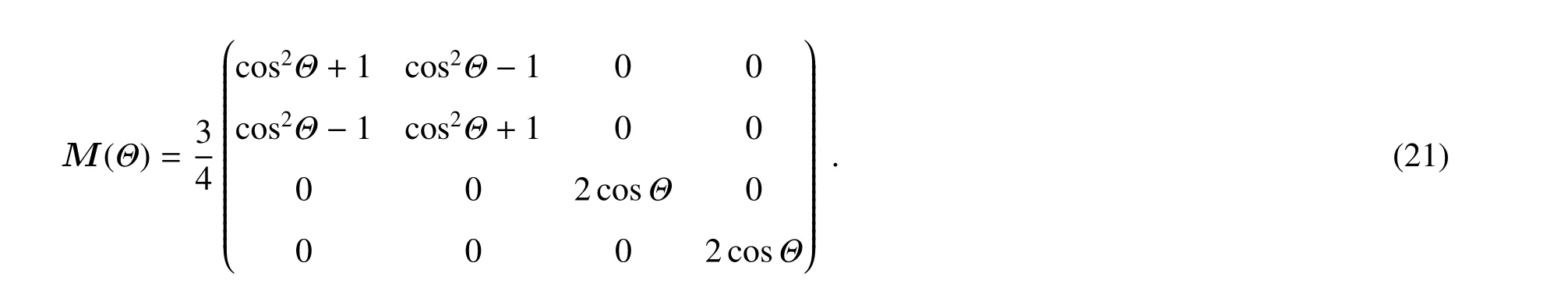
当散射反照率ω=0.5时,采用逆正向蒙特卡罗法得到的介质上表面的Stokes矢量如图7所示,其计算条件为n(z)=1.2+0.6z/L,L=0.1,κa=10m-1,S0=(1,0,0,0)T,200子层,模拟光线的总数量为106。在图7(a)、(b)中I和Q分量数值相对较大,而在图7(c)、(d)中U和V分量非常小,接近0。与图5相比,散射对Stokes矢量的影响是明显的,光线发生了散射,这使得I和Q分量都有所减少。

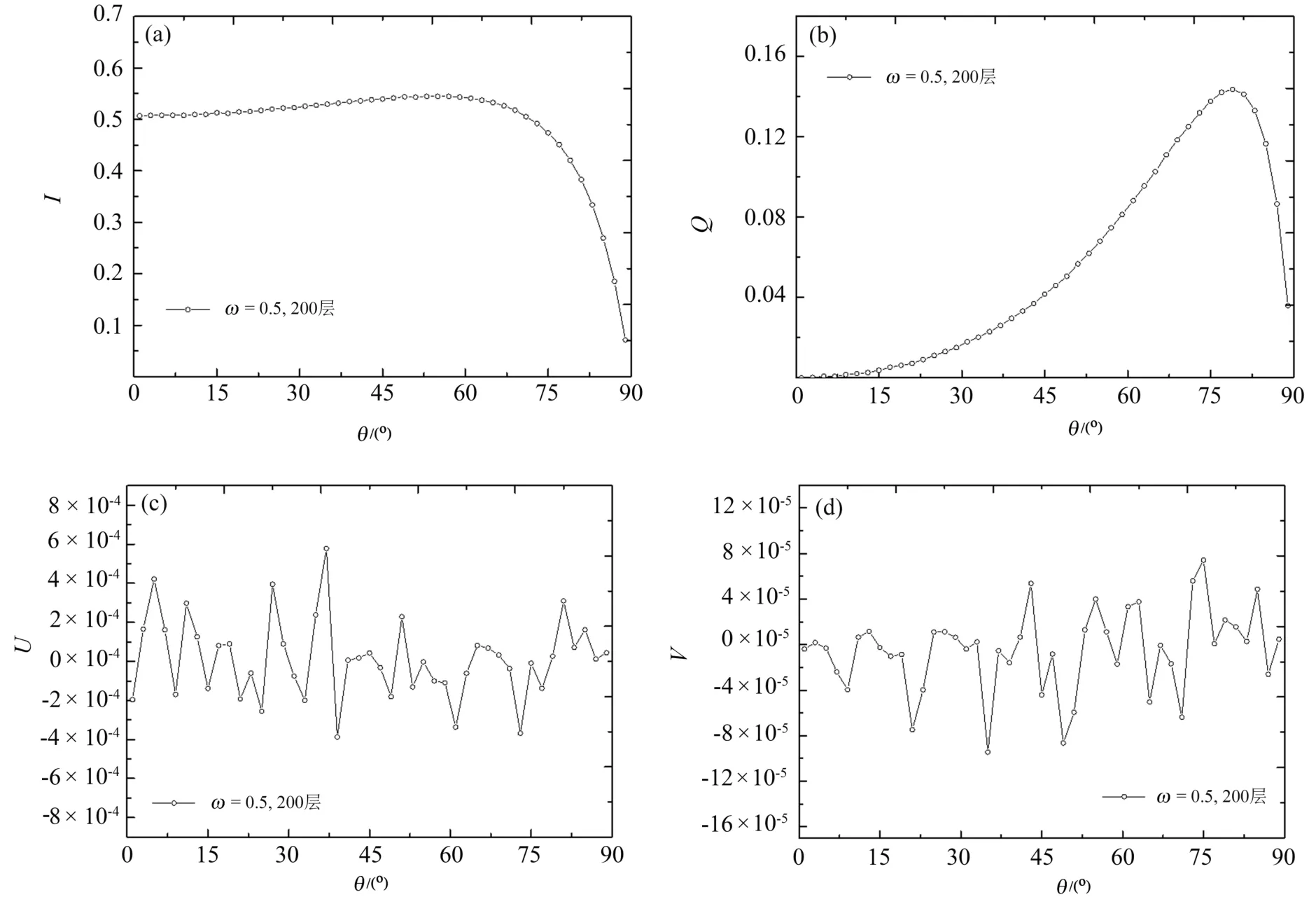
图7 反照率为ω=0.5时介质上表面Stokes矢量。(a)I分量;(b)Q分量;(c)U分量;(d)V分量Fig.7 Stokes vector of upper surface on medium when ω=0.5.(a)I component;(b)Q component;(c)U component;(d)V component

图8是在散射反照率ω=0.5时,采用逆正向蒙特卡罗法和标量反向蒙特卡罗法求得的上表面和下表面某处发射率的对比,图8的计算条件为n(z)=1.2+0.6z/L,L=0.1,κa=10m-1,S0=(1,0,0,0)T,200子层,模拟光线的总数量为106,此时两种方法的计算结果并不完全一致。在散射的条件下,介质中光线被散射的概率增加了,考虑偏振状态时光线散射方向的分布概率与标量不同,因此逆正向蒙特卡罗法发射率的结果与标量方法也存在一定的差异。

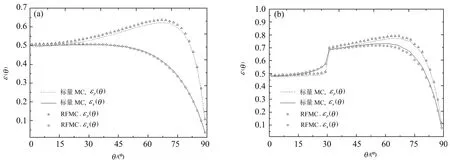
图8 介质上下表面某点的发射率结果。(a)上表面;(b)下表面Fig.8 Emissivity results for a point on the upper and lower surfaces of a medium.(a)Upper surface;(b)lower surface

3 结论

采用逆正向蒙特卡罗法求解了考虑光线偏振情况时一维梯度折射率介质的表观发射特性。分别研究了一维线性折射率分布非散射性介质和各向异性散射介质的表观矢量,得到了Stokes矢量图像,并与已有文献中计算的标量表观发射率结果进行了对比验证。主要内容和结论有:

1)传统的蒙特卡罗法各个子过程之间相互独立且连贯,一个子过程计算结束后才进入下一个子过程。例如在界面反射的子过程中,生成了随机数就立即去判断光线是反射还是透射。而逆正向蒙特卡罗法中,并没有把光线轨迹上事件保持在一个连续的计算过程。各种事件是否发生的判断过程,可以发生在其他子过程中。这使得蒙特卡罗法的应用更为灵活,为解决其他更为复杂问题提供了新的思路。

2)提出了逆正向蒙特卡罗法,实现Stokes矢量反向跟踪正向计算。通过与标量方法的对比和分析,逆正向蒙特卡罗法可以很好解决此类复杂问题,其结果表明考虑光线偏振的表观发射特性与标量方法的结果存在一定的区别。

3)由于介质中梯度折射率的分布,使得介质上下表面的发射率存在了差别。随着光学厚度减小,介质表观Stokes矢量也随之减小,但在较大观测角度呈现复杂结果。在一维梯度折射率介质表面的Stokes矢量图像中,I和Q分量数值较大,而U和V分量非常小。