Boost 型无频闪谐振降压式LED 驱动电源分析与设计

刘文菡，刘雪山，贺明智，周 群，孙 曼

（四川大学电气工程学院，成都 610044）

高亮度发光二极管（high brightness LED）以其光效高、色域宽、寿命长、体积小等优点，被广泛用于替代传统的冷阴极荧光灯和白炽灯[1-2]。为减少电力电子设备对电网的谐波污染，GB/T14549-93 《电能质量公用电网谐波》、欧盟IEC61000-3-2 Class C等标准对电力电子设备输入电流的各次谐波提出了限制要求[3]。因此，研究具有功率因数校正PFC（power factor correction）的LED 驱动电源具有重要意义。

近年来，体积小、效率高的高功率因数单级LED 驱动电源逐渐进入人们的视野。传统的单级Buck PFC 变换器具有开关管电压应力低、效率高以及降压变换的特点，非常适于非隔离型场合。但当输入电压低于输出电压时，输入电流会出现死区，导致功率因数降低，难以达到IEC61000-3-2 Class C 的规定，尤其是当输出电压较高的应用场合[4-5]。传统的单级Buck-Boost PFC 变换器可同时实现升压和降压变换，还具有固有的电流整形能力、成本低的特点。但是，与Buck 和Boost PFC 变换器相比，当开关管关断时，Buck-Boost PFC 变换器的所有输出能量均来自于主电感存储的能量，导致Buck-Boost PFC 变换器的电磁兼容性差、效率低、电流和电压应力高[6]。传统的单级Boost PFC 变换器具有效率高、输入电流纹波低、电磁兼容性好以及具有输入电流整流能力的特点，是PFC 应用中最受欢迎的变换器拓扑结构，特别是当主电感电流工作在临界导通模式时。但是，Boost PFC 变换器只能实现升压变换输出，在一定程度上限制了其作为单级功率变换器的应用范围[7-8]。此外，这3 种PFC变换器的输出电压中含有较大的二倍频纹波，对于一些需要高质量、高精度、低输出纹波供电的应用，这三种单级非隔离式变换器难以满足要求，而且作为LED 驱动电源时还会导致频闪，对人类健康带来一定的影响[9-10]。因此，为了消除LED 频闪，通常需要在单级PFC 变换器后级联DC-DC 变换器以消除二倍频纹波[11]。整合式Boost-Flyback LED 驱动电源通过单个开关管将前级Boost PFC 变换器与后级Flyback DC-DC 变换器进行级联整合，利用一个控制回路实现高功率因数和低电流纹波输出，但其中间储能电容的电压过高会影响电路的性能[12]。二次型Boost 变换器利用单个开关管将前级Boost PFC变换器与后级Boost DC-DC 变换器进行整合，具有高功率因数、低电流纹波输出以及低电压应力的特点[13]。但二次型Boost 变换器的输出电压必须至少高于输入电压的峰值，在一定程度上限制了其应用范围，例如作为LED 驱动电源的使用。在交流输入（200～240 V）功率变换器中，二次型Boost PFC 变换器的输出电压会达到400 V 以上，这使得二次型Boost PFC 变换器主要作为前级变换器使用。

本文基于二次型Boost 变换器提出一种Boost型无频闪谐振降压式LED 驱动电源，利用一个开关管将二次型Boost 变换器与一个谐振网络级联整合。搭建了一台84 W 的实验样机，对该LED 驱动电源理论分析的正确性和可行性进行验证。

1 电路结构

图1 为本文提出的LED 驱动电源的电路及其控制回路。功率回路由整流桥Dbridge、输入滤波电感Lf、输入滤波电容Cf、励磁电感L1及L2、储能电容CB、开关管S1、续流二极管Di（i=1，2，6）、谐振电容Cri（i=1，2）和二极管Dj（j=3，4，5）及谐振电感Lr组成的谐振网络、输出二极管Do、输出电容Co、LED负载以及采样电阻Rs组成。

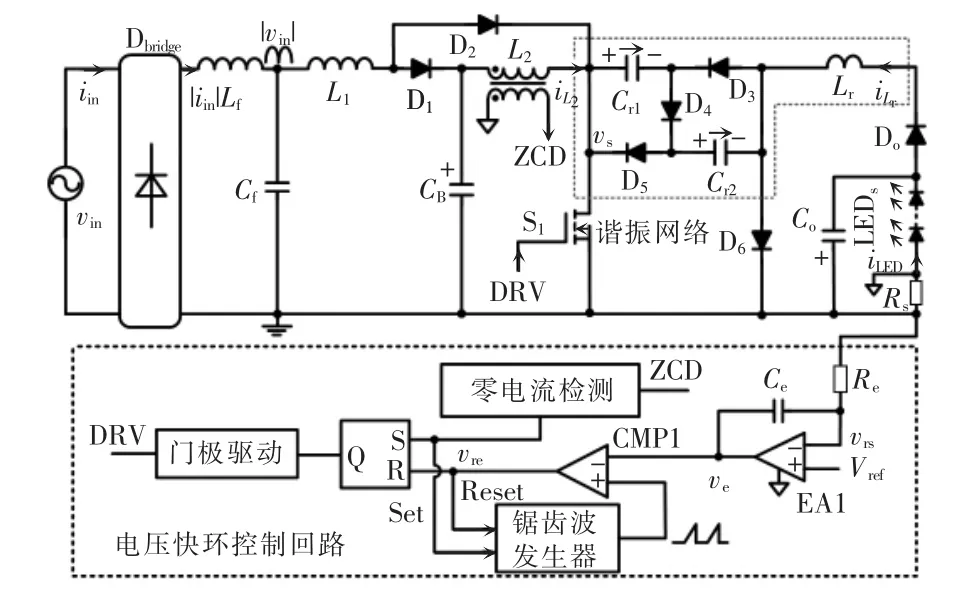
图1 Boost 型无频闪谐振降压式LED 驱动电源及其控制回路Fig.1 Flicker-free resonant step-down LED driver based on Boost topology and its control loop

该LED 驱动电源采用电压快环控制回路实现低纹波恒流输出控制。控制环路中，误差放大器EA1 将输出信号vrs和控制回路参考电压Vref进行比较并得到误差电压ve。比较器CMP1 将ve与锯齿波信号进行比较并得到复位信号vre。输出电流iLED被调整为Vref/Rs，实现恒流输出。当S1关闭时，锯齿波发生器复位至0；当RS 触发器的置位端子为高电平时，锯齿波发生器将被置位。RS 触发器置位端子的输入信号是电感L2的零电流检测ZCD（zero current detection）信号，其中ZCD 信号由电感L2的辅助绕组产生。因此，电感L2的电流工作在临界导通模式CRM（critical conduction mode）。因为CB上的电压纹波较小，在一个工频周期内，开关管的导通时间基本保持不变，因此电感L1的电流工作在断续导通模式DCM（discontinuous conduction mode），即可实现功率因数校正。

当L2工作在连续导通模式CCM（continuous conduction mode）时，由于后级DC-DC 变换单元占空比不随输出负载变化而变化，与前级工作于DCM 的AC-DC 变换单元共用占空比后导致变换器工作不稳定。当L2工作在DCM 时存在电感电流为0 的死区，相对于CCM 和CRM，电感电流峰值增大，使得开关管和二极管的电流应力增大。而CRM是介于CCM 和DCM 之间的一种工作模式，相对于DCM，开关器件的电流应力更低，可以实现续流二极管的零电流关断，且电感更易于设计，故本文将电感L2的电流设计在CRM 下。

2 工作原理分析

为简化分析过程，做如下假设：①所有元件均为理想器件；②开关频率fs远大于工频频率fL，即fs≫fL；③输入电压为全波整流后的电压，即|vin（t）|=Vm|sin（ωt）|，其中Vm为输入电压峰值，ω=2πfL为输入电压的角频率；④谐振电容Cr1、Cr2相等，即Cr1=Cr2=Cr；⑤输出电容Co足够大，其电压纹波忽略不计。当电感L2工作在CRM 时，存在2 种不同的工作条件：ton＞Tr/2 和ton＜Tr/2，ton和Tr分别为开关管的导通时间和谐振周期。与ton＜Tr/2 相比，ton＞Tr/2 可以实现二极管的零电流关断，减小电路损耗，因此本文主要针对ton＞Tr/2 的情况进行分析。

图2 为电感L1与L2电流分别工作在DCM、CRM下的主要波形。在一个开关周期Ts内，该LED 驱动电源存在4 个工作模态，其模态电路如图3 所示。

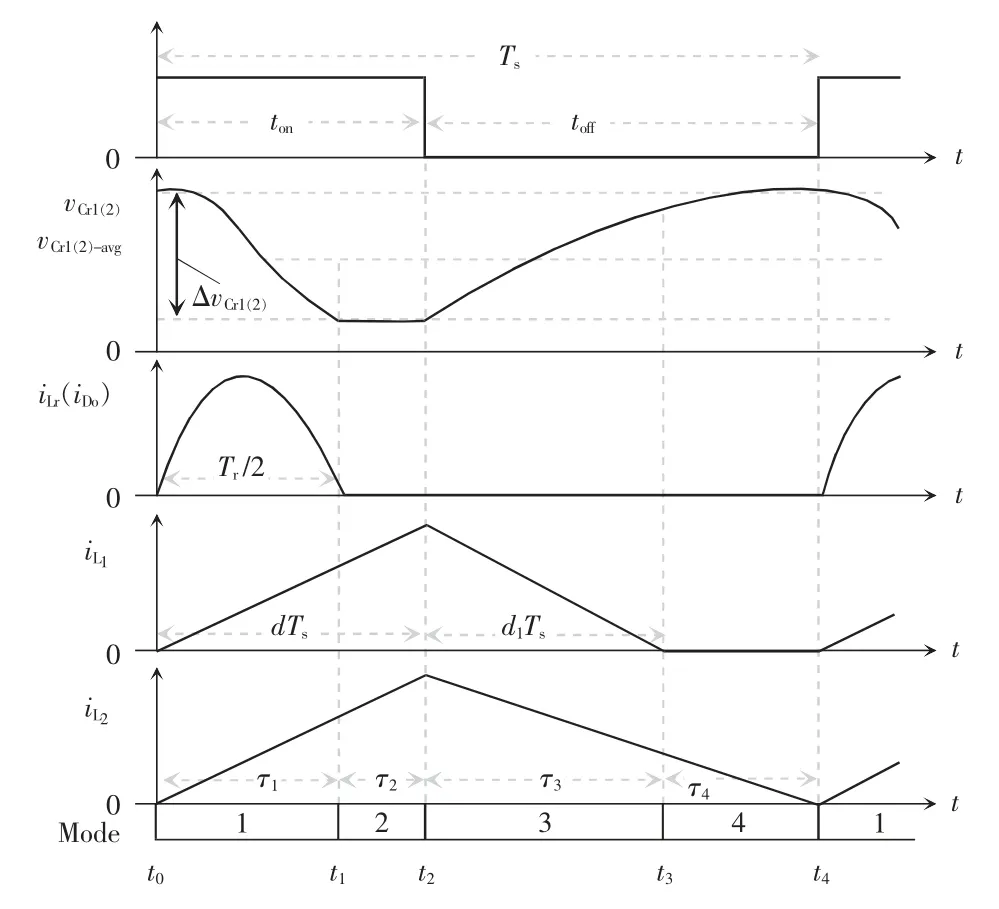
图2 本文LED 驱动电源的主要波形Fig.2 Key waveforms of the proposed LED driver

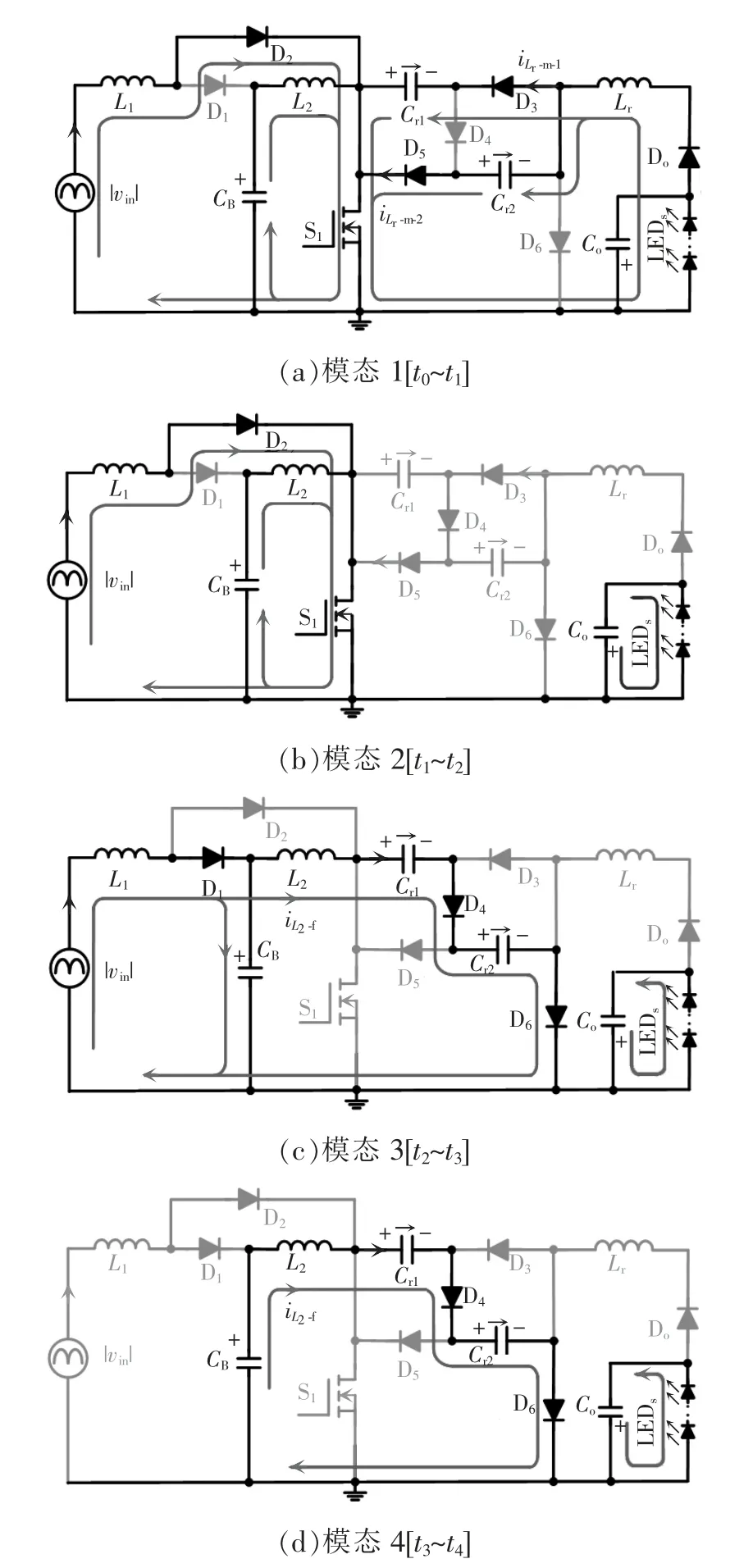
图3 各模态的等效电路Fig.3 Equivalent circuits in different modes

模态1[t0～t1]：如图3（a）所示，t0时刻，开关S1导通，二极管D1承受反向电压关断，D2承受正向电压导通，电源|vin|给电感L1充电，电容CB给电感L2充电，电感L1、L2的电流iL1、iL2线性上升，则有

式中：vin为输入电压；VCB为CB两端电压。

同时，二极管D3、D5和Do承受正向电压导通，二极管D4和D6承受方向电压关断。谐振电容Cr1、Cr2并联后通过开关管S1与谐振电感Lr发生串联谐振，能量从谐振电容Cr1、Cr2转移到输出支路LEDs。谐振电感Lr两端的电压为vCr1-vo。因此可得

根据式（2），谐振电流iLr（t）为

式中：vC1（t0）为t0时刻谐振电容Cr1两端的电压；ω0和Z0分别为谐振网络的角频率和等效阻抗，ω0=1/。当谐振电流iLr（t）谐振到0时，二极管D3、D5和Do零电流关断，模态1 结束。模态1 的工作时间为

模态2[t1～t2]：如图3（b）所示，t1时刻，开关管S1保持导通，因此电感电流iL1（t）、iL2（t）以模态1 的斜率继续线性上升。因为谐振电流iLr（t）为0，故二极管D[i]（i=3，4，5，6）和Do均承受反向电压关断。t2时刻，开关管S1关断，模态2 结束，此时电感电流iL1（t）、iL2（t）均达到最大值，即

式中，ton为开关管的导通时间。模态2 的工作时间为τ2=ton-Tr/2。

模态3[t2～t3]：如图3（c）所示，t2时刻，开关管S1关断，二极管D2、D3、D5和Do承受反向电压关断，二极管D1、D4和Do承受正向电压导通。此时，输入电压|vin|与电感L1、L2共同给后级供电，电流iL1-iL2给储能电容CB充电，电感电流iL2通过D4和D6给谐振电容Cr1、Cr2充电。L1两端的电压为|vin|-VCB，L2两端电压为VCB-vCr1-vCr2，电感电流iL1（t）、iL2（t）线性下降，则有

当电感电流iL1（t）下降到0 时，模态3 结束。模态3 的工作时间为τ3=d1Ts，其中d1为电感L1的放电占空比。

模态4[t3～t4]：如图3（d）所示，在此模态开关管S1仍保持关断，二极管D2、D3、D5和Do仍保持关断，电感电流iL1（t）下降到0，二极管D1关断。电感L2与电容CB串联给谐振电容Cr1、Cr2充电，电感电流iL2继续以模态3 的斜率线性下降。当电流iL2下降到0时，该模态结束，开始下一个开关周期。模态4 的工作时间为τ4=toff-τ3，其中toff为开关管S1的关断时间。

3 电路特性分析

3.1 电压增益分析

根据电路的模态分析可知，在一个开关周期Ts内，由电感L1、L2以及Lr的伏秒平衡可得

式中：vCr1（2）（t）为谐振 电 容vCr1（2）的电 压；vCr1（2）-avg为 谐振电容Cr1（2）在一个开关周期内的平均电压；d 为开关管S1的导通占空比。由式（6）可得

由式（7）可知，开关管S1的导通占空比与电容CB电压和输出电压有关。因此可得电压增益为

当d＜d1/（1+2d1）时，该变换器可以实现降压输出，适用于LED 驱动电源。

3.2 输入电流分析

图4 为该LED 驱动电源在半个工频内的电感电流iL1波形与控制时序。由第2.1 节分析可知，一个开关周期内，整流后的输入电流|iin|等于电感L1的平均电流，故

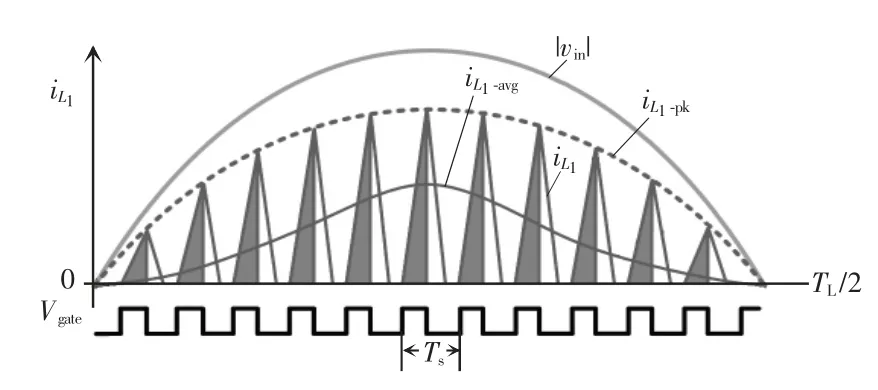
图4 半个工频周期内电感电流iL1波形和控制时序Fig.4 Waveforms of inductor current iL1 and control sequence in a half of power frequency cycle

由式（9）可知，输入电流与输入电压|vin|、开关频率fs、d、VCB以及L1有关。

3.3 开关频率分析

由第2.1 节模态分析可知，在一个开关周期Ts内，电感L2的平均电流为

在半个工频周期内，假设能量传递效率为100%，根据功率守恒可得

将式（9）与式（10）代入式（11），可得

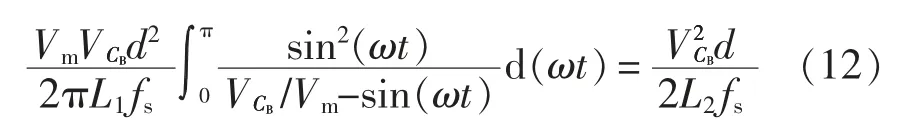
对于二次型Boost 变换器，当1＜VCB/Vm＜5 时即可满足绝大部分的应用，故利用Matlab 进行曲线拟合，得到

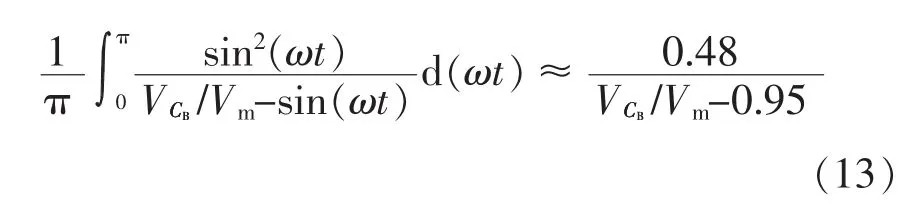
根据式（7）、式（12）和式（13），VCB可表示为

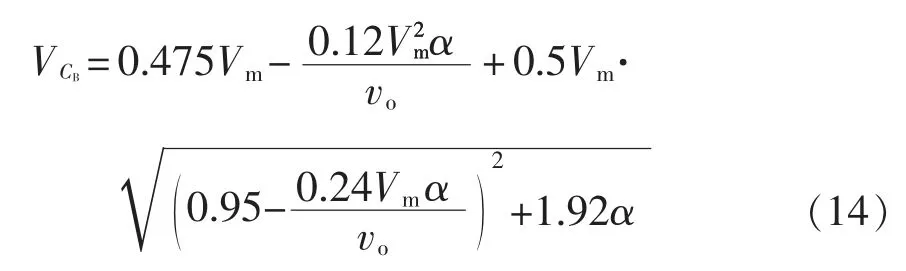
式中，α 为电感比，α=L2/L1。由式（14）可知，当输入、输出电压一定时，VCB由α 决定。

由式（6）、式（10）和式（11）可知，开关管的导通时间和关断时间分别为

则开关管的开关频率fs为

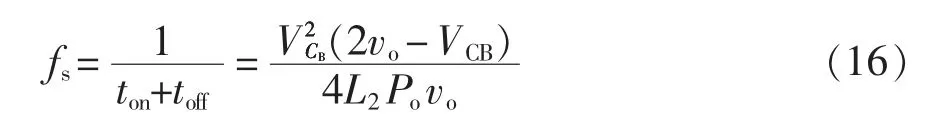
由式（14）和式（16）可知，当输入、输出电压一定时，开关频率fs与电感L1、L2有关。根据式（16）在交流输入电压200～240 V，vo=280 V，Po=84 W，以及L1=530 μH、L2=2.65、3.71、4.10、4.77、5.30 mH 即α为5、7、7.74、9、10 条件下，开关频率fs与输入电压的关系曲线如图5 所示。

图5 开关频率fs 与输入电压关系曲线Fig.5 Curve of relationship between fs and input voltage

由图5 可知，对于相同的α，开关频率fs随输入电压的增大而减小；反之，对于相同的输入电压，fs随α 的减小而增大。fs过高会导致开关管的损耗增大，但为了避免音频噪声，fs必须高于20 kHz。因此，与传统的二次型Boost 变换器相类似，电感L1与L2的选择对优化电路的效率具有重要意义。

3.4 功率因数与开关管应力分析

由式（9）与式（11）可得该LED 驱动电源的功率因数为

根据式（17）得出L1=530 μH、L2=4.1 mH、输出电压vo=280 V 条件下，PF 与输入电压vin的关系曲线，如图6 所示。由图6 可知，PF 随着vin的增大而减少，当vin为220 V 时，PF 为0.976。

图6 不同输入电压下的PF 曲线Fig.6 Curve of PF under different input voltages

由图2 和图3 可知，在一个开关周期Ts内，谐振电容Cr1（2）在模态1 放电，在模态3 和模态4 充电。因此，根据电容Cr1（2）的电荷平衡原理有

式中：Q（k）dis、Q（k）ch分别为谐振电容Cr（k）（k=1，2）在一个开关周期内的放电电荷和充电电荷；ΔvCr（k）为谐振电容Cr（k）（k=1，2）在一个开关周期内电压变化量。根据式（18）可得

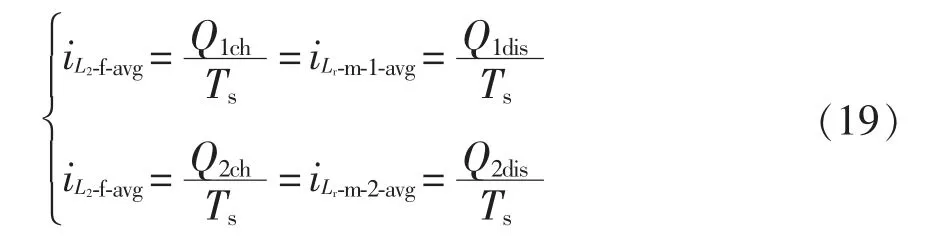
式中：iL2-f-avg为模态3 和模态4 中从电感L2流向谐振电容Cr1（2）的电流；iLr-m-1-avg和iLr-m-2-avg分别为模态1中谐振电容Cr1和Cr2流向谐振电感Lr的电流。

由式（18）和式（19）可知，当Cr1=Cr2=Cr时，

因此，谐振电容Cr1的充电电荷可以表示为

由式（4）、式（5）和式（21）可得谐振电容的电压变化量为

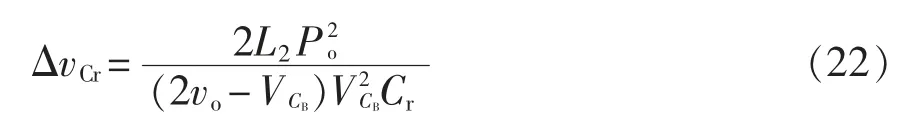
如图3 所示，开关管S1在模态3 和模态4 时承受反向电压应力，因此，开关管S1的最大电压应力为

由上可知，开关管的最大电压应力随着输出电压的减小而减小。在模态1 时，流过开关管S1的电流为iL1（t）+iL2（t）+iLr（t），当|sin（ωt）|=1 时，电流应力最大。因此，由式（1）和式（3）可得，开关管S1的最大电流应力为

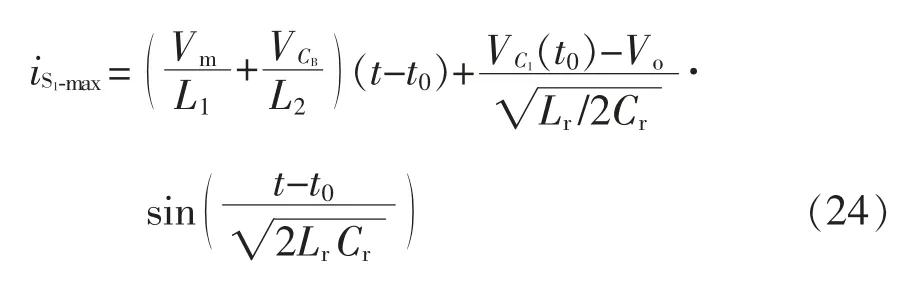
由式（24）可知，开关管的电流应力与谐振电容Cr以及谐振电感Lr有关。当谐振电容一定时，开关管的最大电流应力iS1-max随着谐振电感Lr增大而减小。但过大的谐振电感值会导致ton＜Tr/2，使得二极管D3、D5和Do不能零电流关断，效率降低。

3.5 电感、电容的设计分析

根据式（11），当L1和L2分别工作在DCM、CRM 时，输出功率可以表示为

其中，m1=VCB/Vm，m2=vo/Vm。

根据式（4）可知，电感L1的峰值电流随着输入电压的变化而变化。在半个工频周期内，当|sin（ωt）|=1 时，最大峰值电流为

半个工频周期内，随着电感L1的增大，电感电流iL1将在输入电压为最大值时进入CRM。当电感电流iL1工作在CRM 时有

式中，iL1-avg-max为半个工频周期内电感L1的最大平均电流。

根据式（9）、式（25）～式（27），半个工频周期内最大输入电压时，L1的临界电感为

为了使该LED 驱动电源工作在ton＞Tr/2 条件下，谐振电感Lr与谐振电容Cr应满足

图7 为Po=84 W、vo=280 V 时，LrCr最大值与输入电压的关系曲线。由图7 可知，当α 一定时，LrCr最大值随着输入电压的增大而减小；当输入电压一定时，LrCr最大值随着α 的增大而增大。由式（22）可知，谐振电容Cr越大，其纹波越小，从而提高LED 驱动电源的效率，但电容过大会增加驱动电源的体积。因此，应合理选择谐振电容。当谐振电容确定后，根据式（29）即可确定Lr。

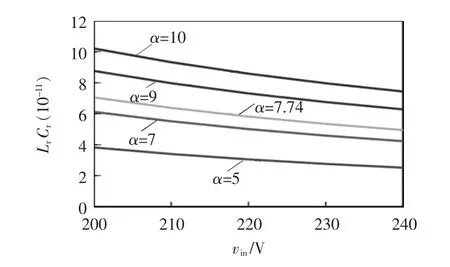
图7 LrCr 最大值与输入电压关系曲线Fig.7 Curve of relationship between maximum LrCr and input voltage

由以上分析可知，基于储能电容CB容值足够大，电容上的工频纹波可以忽略。但在实际应用中，储能电容容值不可能无限大，需要考虑电容的工频纹波电压对电路的影响。

该变换器的第二级可等效为一个阻抗RB，有

其等效电路如图8 所示。在一个开关周期内，流过二极管D1的平均电流可以表示为

图8 等效电路Fig.8 Equivalent circuit

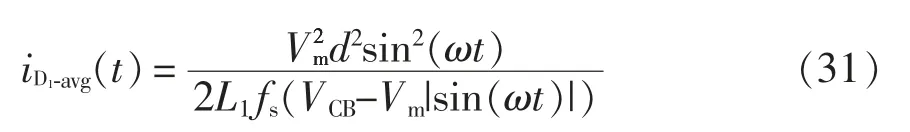
利用傅里叶变换，式（31）可以表示为

由式（30）～式（33），VCB可以表示为

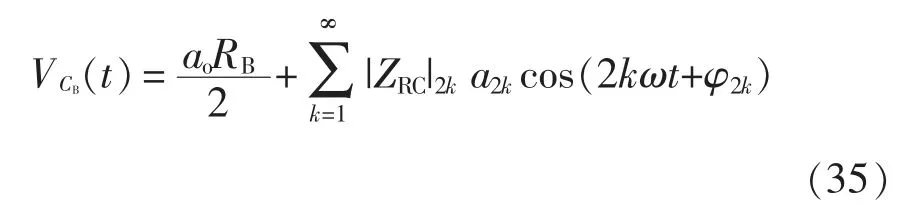
式中，vrip[2k]（t）为VCB的电压纹波。

通常k=1 即可满足储能电容电压VCB的精确度。假设电容CB的电压纹波中只包含二次谐波，因此

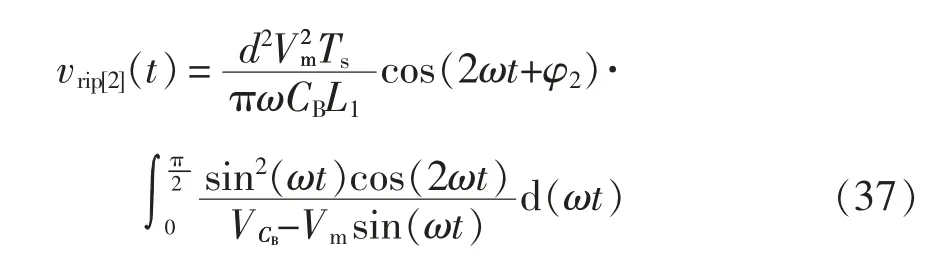
考虑储能电容CB的电压纹波对电路参数以及性能的影响，由式（7）、式（9）和式（37），开关管的导通占空比以及输入电流可以表示为

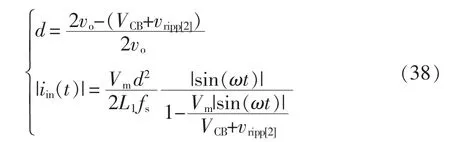
基于vin=220 V、L1=530 μH、L2=4.1 mH、vo=280 V以及Po=84 W，绘制式（37）和式（38）对应的波形图。图9 所示为不同CB下CB的电压纹波以及开关管导通占空比的变化曲线。由图9 可知，CB的电压纹波和d 的变化范围均随着储能电容CB的增大而减小。

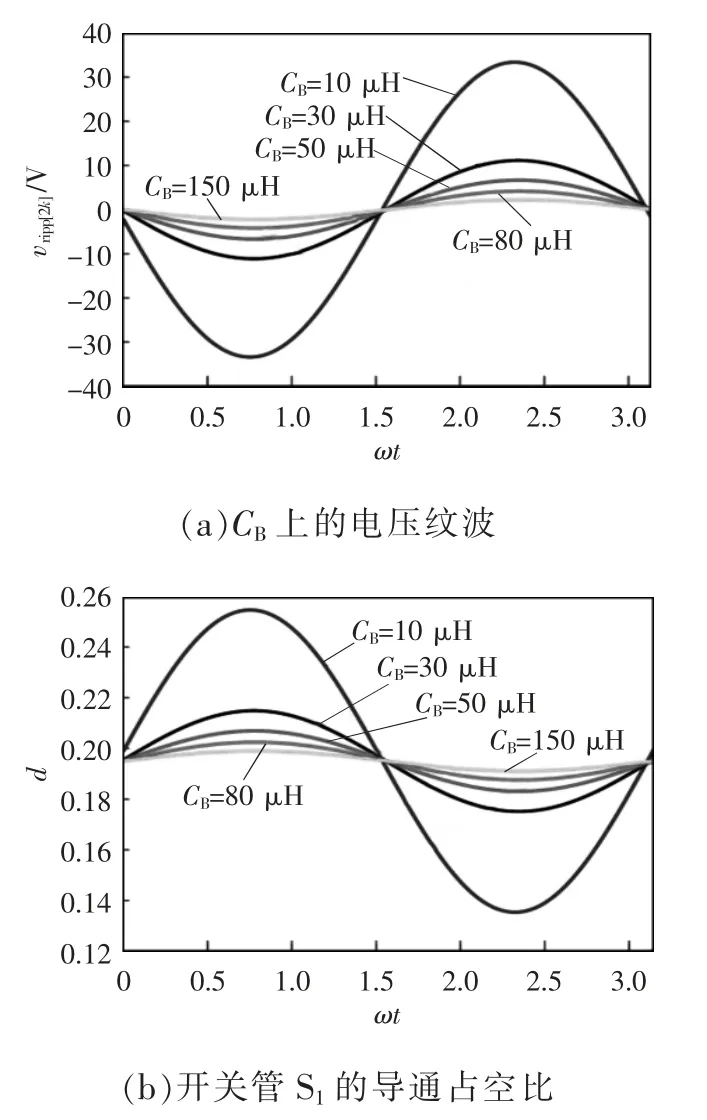
图9 不同CB 的变化曲线Fig.9 Curves with different values of CB

图10 为不同CB下输入电流的变化曲线。由图10 可知，不同CB下，输入电流的波形均有明显失真，随着CB的增大，输入电流的失真得到改善。

图10 CB 对输入电流的影响Fig.10 Effect of CB on input current

本文分析的LED 驱动电源中谐振网络只含有2 个谐振电容。实际上，可以根据具体的应用场所，以相同的级联方式增加谐振网络中谐振电容和二级管的数量，可以得到具有n 个谐振电容的谐振网络，从而得到更多降压变换输出的LED 驱动电源。但随着谐振电容和二极管的增加，LED 驱动电源的效率会有所下降，这主要是由二极管的管压降造成的。

4 实验验证

为了验证上述理论分析的正确性及可行性，搭建一台84 W、交流输入电压范围为200～240 V 的LED 驱动电源实验样机，开关管S1型号为15NM 65。实验参数如表1 所示。

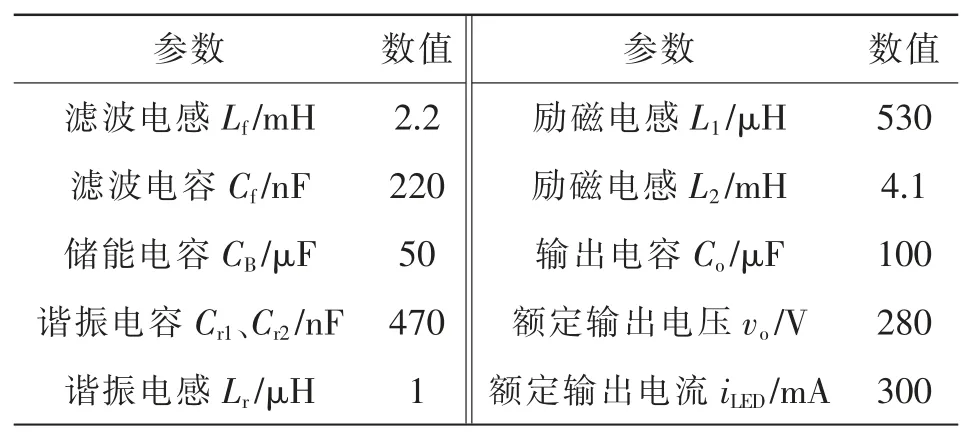
表1 实验样机的电路参数Tab.1 Circuit parameters of experimental prototype

由式（22）可知，谐振电容Cr1和Cr2取较大值时可以有效减少谐振电容上的电压纹波，从而提高该LED 驱动电源的效率。但是谐振电容Cr1和Cr2取值过大会增加驱动电源的体积。综合考虑，本文中Cr1和Cr2取值为0.47 μF。确定谐振电容的容值后，考虑式（29）以及有效减少谐振电感Lr的体积，谐振电感Lr取值为1 μH。该LED 驱动电源采用FL6961 控制芯片对输出电流iLED进行控制。图11所示为该LED 驱动电源的实验样机。

图11 实验样机Fig.11 Experimental prototype

当交流输入电压vin为220 V 时，该LED 驱动电源的输入电压vin、输入电流iin以及输出电流iLED波形如图12 所示。由图可知，输入电流与输入电压波形同相位，输入电流波形畸变较小，表明该LED驱动电源可以很好地实现功率因数校正，由Tektronix PA1000 功率分析仪测得此时的PF 值为0.979。此外，该LED 驱动电源实现了300 mA 的低纹波输出电流且其闪烁比为5.7%，低于8%，满足IEEE 标准1789-2015[14]。

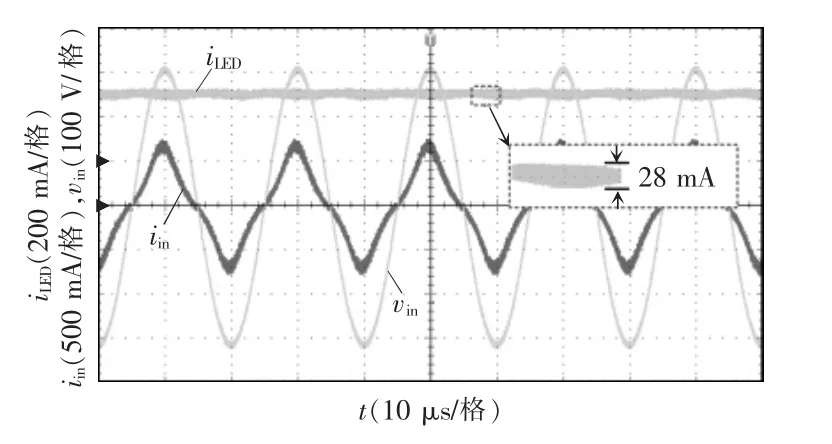
图12 输入电压Vin、输入电流iin 以及输出电流iLED 波形Fig.12 Waveforms of input voltage Vin,input current iin and output current iLED

图13 为交流输入电压220 V 时，该LED 驱动电源的主要波形。

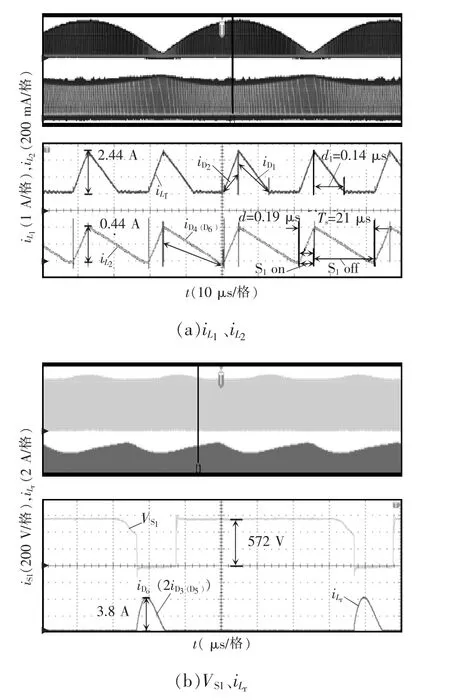
图13 交流220 V 时的主要波形Fig.13 Key waveforms under ac 220 V voltage

由图13（a）可知，该LED 驱动电源的电感L1和L2分 别 工 作 在DCM、CRM，Ts为21 μs，fs为47.619 kHz，由式（16）可知，当输入电压为220 V 时，Ts理论值为17.386 μs，fs理论值为57.516 kHz。开关频率的理论值和测试值之间的误差主要是由于L2电感电流续流到0 时，MOSFET 的输出电容Coss与L2谐振导致的ZCD 检测延迟引起的[15]，因此，在实际计算中此处需考虑其影响并留一定的设计余量。由图13 可知，d 为0.19 μs，d1为0.4 μs，d=0.19 ＜d1/（1+2d1）=0.222，由式（8）可知，该LED 驱动电源实现了降压变换输出，电压增益M 为0.91。由图13（b）可知，开关管的电压应力为572 V，低于S1的最大反向电压。由式（23）可知，输入电压为220 V 时，开关管S1的电压应力为565.6 V，与实验结果相近。此外，由图13（b）可知，谐振电感电流iLr的波形非完全的正弦波形，在电流下降段存在一定的近似线性的拖尾，这主要是由实际中开关管的导通电阻造成的。

为了验证该LED 驱动电源的动态性能，图14给出了输入电压从200 V 阶跃到240 V 时整流后的输入电压|vin|、输出电流iLED以及电感电流iL2的波形。由图14 可知，当输入电压从200 V 阶跃到240 V 时，电流iLED以及iL2快速实现了稳定且输出电流iLED不变，表明该LED 驱动电源具有良好的动态特性且实现了恒流输出。

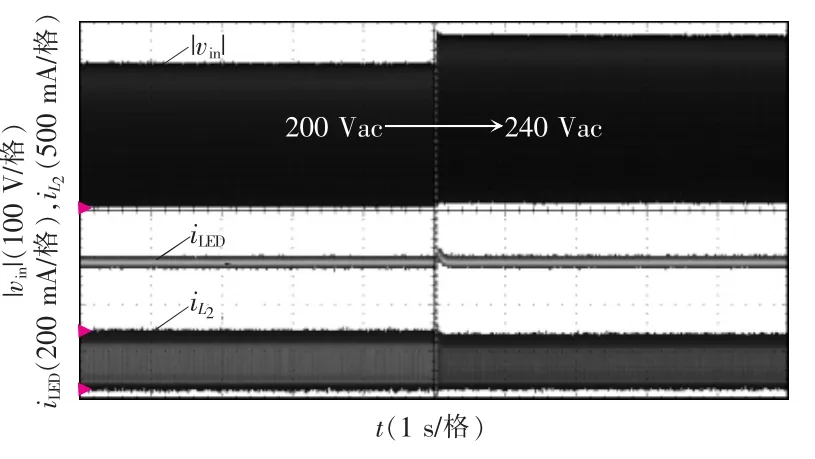
图14 输入电压由200 V 跳变到240 V 的主要波形Fig.14 Key waveforms when input voltage suddenly changes from 200 to 240 V voltage

图15 为输入电压为200～240 V 时，该LED 驱动电源的PF、效率以及输入电流的谐波含量曲线。由图15（a）可知，在200～240 V 输入电压范围内，PF 高于0.97，且随着输入电压的减小而增大。同时，该LED 驱动电源的效率随着输入电压的增大而增大，效率最大可以达到92.88%。由图15（b）可以看出，该LED 驱动电源的各次谐波含量均满足IEC61 000-3-2 Class C。

图15 PF、效率以及输入电流的谐波含量曲线Fig.15 Curves of PF,efficiency and harmonic content of input current

5 结语

本文基于二次型Boost 变换器提出并研究了一种Boost 型无频闪谐振降压式LED 驱动电源，并对其工作原理以及电路特性进行了分析。该LED 驱动电源利用一个开关管将二次型Boost 变换器与一个谐振网络级联整合，控制简单。利用该电路结构拓扑，该LED 驱动电源可以实现高效率和低电流纹波输出。与传统的二次型Boost 变换器相比，该LED 驱动电源可以实现降压变换输出，适用于高功率因数无频闪LED 驱动电源。最后，搭建了一台84 W 的实验样机，效率最高可达到92.88%，验证了本文提出的LED 驱动电源的正确性和可行性。