三端口双向直流变换器断路故障综合诊断方法

陈周牛，谷伟平

（重庆人文科技学院机电与信息工程学院，重庆 401524）

当前三端口双向直流变换器技术随着微电子技术、功率半导体制造技术及其边沿技术的快速发展，逐渐得到飞跃进展[1-2]。三端口双向直流变换器的应用范围较为广泛，如医疗、通信、新能源发电系统及航天航空等领域，具有多变的输出样式、较高的效率及较宽的稳压范围等特点[3-4]。但是三端口双向直流变换器在运行时若有故障出现，且不能快速对出现的故障进行隔离，便会产生整体系统崩溃的严重后果。为此越来越多的国内外学者加入到对三端口双向直流变换器故障诊断的研究中[5-7]。

三端口双向直流变换器中所出现的故障，大部分为功率开关管的断路与短路故障[8]，这是由于功率开关管是三端口双向直流变换器中比较脆弱的一部分。其若发生故障，其所在电路内其余元器件的电流与电压应力均会增长，此时若未能对故障迅速处理，便可能造成严重的二次（回路）故障，导致整体系统崩溃[9]，所以对三端口双向直流变换器中功率开关管的故障诊断方面，更多学者相继展开研究[10]。其中，Park T 提出了一种基于电感电流斜率的故障诊断方法，此方法是针对boott 变换器而言的故障诊断方法，Shahbazi M 提出了一种基于现场可编程门陈列FPGA（field-programmable gate array）的实时故障诊断方法，此方法对Park T 提出的方法进行了有效改进；对开关管断路和短路的诊断以对直流侧电流的检测方法而得到实现，此方法由Kim S Y 提出，是针对全桥零电压开关ZVS（zero voltage switch）变换器而言的诊断方法。

综上所述，以上各学者所提出的故障诊断研究方法存在诊断时间长或诊断成本高等缺陷，为此，本文提出一种基于遗传算法的BP 神经网络诊断方法，此方法对于三端口双向直流变换器的故障诊断具有省时、效率高的特点。

1 三端口双向直流变换器设计

1.1 三端口双向直流变换器的工作原理

在SHEV 电气驱动系统内可达到转换功率、速度与频率调节的核心装置即为三端口双向直流变换器。变换器拓扑形式与传统T 型三电平AC-DC变换器类似，分离出直流侧的一个分压电容作为蓄电池端口，交流侧与直流输出、蓄电池端口之间均为单级功率变换[11]。三端口双向直流变换器的仿真拓扑如图1 所示。图1 中的交流系统频率与电源电压分别为50 Hz、220 V，高频隔离变压器Th的变比为1∶1∶1，漏感LPa=LPb=LPc，且其三端是对称的半桥结构。

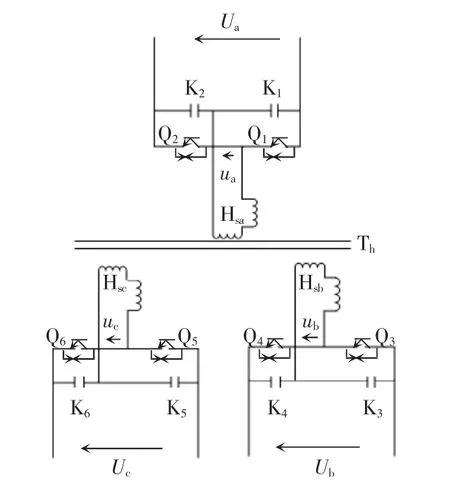
图1 三端口双向直流变换器仿真拓扑Fig.1 Simulation topology of three-port bidirectional DC converter

在有功功率输入与输出情况下，三端口双向直流变换器的各端口均能够工作。由每个桥臂开关管脉冲移向操控策略对三端口双向直流变换器的不同端口间的能量流动情况实行操控。在对高频隔离变压器T 实行等效操作时可将激磁电感忽视，并通过三绕组变压器中三角形模型实现等效操作。将3 个电压源相连的电感网络为Th，Q1与Q3、Q1与Q5各开关管间的脉冲移相角依次以ϕab、ϕac表示，且ϕab＞ϕac。通过了解不同桥臂开关管的情况，依据上下开关管的通断情况，设变压器各端口相对的脉冲电压依次为ua、ub、uc。以ua为参考，ub、uc的移相角分别为ϕab、ϕac，当电压比参考电压超前时其移相角设为负，滞后时则设为正。通过ϕab、ϕac可对3 个端口间能量的流动实现控制。当ϕab＞0、ϕac＞0、ϕab＞ϕac时，能量从ua流向ub、ua流向uc、uc流向ub。此时，ua作为电源，ub作为负载。图中箭头方向代表能量流动方向。

1.2 三端口双向直流变换器故障类型分析

电力电子器件断路与单相接地故障是三端口双向直流变换器故障中较为多见的故障[12-14]，在此本文主要研究电力电子器件的断路故障特点。对此断路故障实行分类时可依据出现断路故障的数量、部位及经仿真研究所得直流侧母线电流波形实现。三端口双向直流变换器故障类型见表1。

表1 中的M 与T 分别表示断路故障与正常运行状态。因3 个或大于3 个器件共同产生故障的概率较低，故在此不做研究。

在对故障特点信号进行选择时，因考虑到某些故障带来的电压降和谐波的改变可通过逆变器与整流器间的电容实现补偿，造成无法正常检测到故障，所以将直流侧电流信号作为故障信号。在系统有故障出现时，电路的情况能够通过直流侧电流信号波形的变化信息给予反馈。整流电流的谐波是通过整流电压的谐波决定的，因6 脉波整流电压的谐波次数是6k（k=1，2，…），故整流电流的谐波次数同为6k。由此可见，通过各种频率成分组合而成的此电流信号，其不同频率成分信号囊括了对应的不同故障信息。所以，为对系统的不同故障情况进行表征，应处理整流侧输出直流电流，并将恰当的频率段信号当成故障特点信息量。

1.3 故障综合诊断方法

1.3.1 故障综合诊断方法过程

故障综合诊断方法过程如图2 所示。从待测三端口双向直流变换器中采集信号，并采用快速傅里叶变换FFT（fast Fourier transform）方法分解信号获取不同频率端，将信号划分成测试样本和训练样本，其中训练样本用于训练完成拓扑结构构件以及权值和阈值设置的神经网络，采用训练完的神经网络对测试样本进行测试，依据测试误差计算法中的个体适应度，采用适应度高的染色体进行复制、交叉以及变异差值，获取新群体，并判断新群体是否满足终止条件，满足则停止迭代运算，并获取最佳神经网络权值的阈值，不满足则对神经网络权值和阈值进行重新复制，并再次循环运算，直至获取最佳群体。总体上看，本文方法进行三端口双向直流变换器断路故障综合诊断的过程为：将直流侧母线输出电流作为特征量，对不同故障类型进行细致分类之后，研究各故障下所输出的电流特性，以FFT分解信号，获取各个频率段，并结合遗传算法BP 神经网络综合实现故障诊断。

图2 BP 神经网络故障综合诊断方法过程Fig.2 Process of comprehensive fault diagnosis method based on BP neural network

1.3.2 故障特点提取

因某些故障带来的电压降和谐波的改变可通过逆变器与整流器间的电容实现补偿，造成无法正常检测到故障，故将直流侧电流信号Idc作为故障特点信号，通过FFT 分解信号获取差异频率段，故障诊断特征量为20 kHz 频率段直流侧电流信号能量，为完成三端口双向直流变换器断路故障综合识别与诊断，采用基于遗传算法的BP 神经网络故障诊断方法实现。

将采集到的信号数据进行适当处理，可提升故障类别与故障元件检测的准确率，具体处理步骤为：

（1）对电机常规运行状态下的直流侧电流幅值iedc进行计算时，可由驱动操控器内的每个功率开关的开关情况信息与每相电流值实现运算，运算出的电流幅值即为桥臂上下2 个功率开关在各种开关情况下的常规电流。

（2）将现实检测的直流侧电流值idc同常规运行状态下运算所得的电机直流侧电流iedc进行对比，若两值存在误差，那么表明已产生故障。

（3）因仿真实验均以理想运行情况存在，但现实中电机运行时的检测信号易被传感器等附加元件所干扰，导致运算值和检测值之间出现误差。所以要避免这种误差的产生，需将特点量g 引入，用以衡量iedc和idc之间的误差，并诊断所产生的故障。特点量g 的表达式为

式中，ib为所选择的边界值，其最大值应小于参考相电流，最小值应大于idc和iedc之差的绝对值。

经实验验证，idc和iedc之差的幅值随参考相电流的增长而增长；在不同负载运行时，idc和iedc之差的幅值依然随之改变。故边界值ib属于一个参考相电流Iref的函数，而不是一个常数，其计算公式为

式中，函数中系数的确定是通过数次变负载与空载实验得出的。

当idc和iedc之差是负值时，即特点量g=-1，idc＜iedc，说明供电电源向电机提供的能量比常规情况下电机应具备的能量低，此时功率管产生断路故障；当idc和iedc之差是正值时，即特点量g=1，idc＞iedc，说明供电电源向电机提供的能量比常规情况下电机应具备的能量高，此时功率管产生短路故障。但是对于故障元件与故障相依然不能通过此特点量精准检测到。由直流侧电流可轻松地反馈出功率变换器所产生的单故障，此时会有和常规情况不等的电流从故障相绕组经过。由于idc和iedc之差的绝对值对应故障相电流的幅值，所以将变量en引入，此变量即为故障相电流in和|idc-iedc|的关系，可表示为

对故障相和故障类别的判断在此引入第2 个特点量Pn，其表达式为

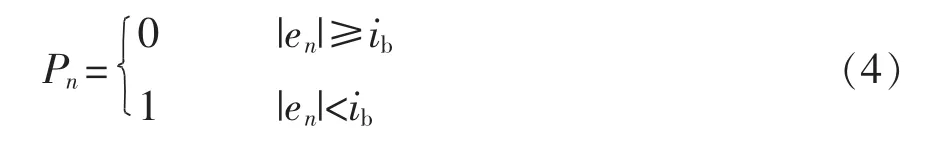
当特点量Pn=1 时，表明电机的第n 相产生故障；由于偶尔会有数个Pn=1 共同产生，因此须确定仅有一个Pn=1 时，方可确认有故障产生。

1.3.3 BP 神经网络

由于BP 神经网络存在学习收敛速率低的缺点，对整体最小点无法确保能够收敛得到[15-16]，为提高故障模式的识别效果，此算法通过遗传算法对BP神经网络的起始阈值与权重值进行优化，提升优化之后的BP 神经网络对故障实行分类的精准度。

在创建BP 神经网络时，三层神经网络便可妥善处理普通模式识别问题，其中隐层神经网络数量n2与输入层神经元数量n1间的关系可表达为

S 型正切函数与S 型对数函数分别为神经网络的隐层神经元与输出层神经元二者的传递函数，为实现最低网络输出误差，应通过Levenberg-Marquardt算法训练网络，并对阈值与权值持续进行修正。

为确保预估结果更精准，本文修正时有别于以往的BP 神经网络所使用的随机权值与阈值，而是采用支持向量机算法来对获取输出误差最低的最优权值与阈值进行修正。

1.3.4 修正方法

使用支持向量机进行修正，支持向量机是一种数据挖掘方法，其是建立在统计学理论基础上的一种新型智能技术，在解决小样本、非线性和高维模式识别问题中，支持向量机算法具有许多独特的优势，非常适合解决故障模式的识别问题。

（1）选择被测电路的典型状态，输入测试激励，利用测试平台测量电路在正常和故障状态下的数据，将其利用小波包分解进行预处理，为了区分不同的故障，对特征数据也进行归一化处理到[-1，1]，构造样本集（xi，yi），i=1，2，…，n，其中xi是电路板在各典型状态下的数据特征，而yi∈[-1，1]标志电路板的状态。如果yi=1，表示电路板处于正常状态；若yi≠-1，表示电路板处于某个故障状态。

（2）对支持向量机进行训练，根据各电路的实际情况选择不同的核函数，训练完毕后，就可以得到各典型状态下的特征数据与电路板的典型故障之间的映射关系,其模型为

支持向量机的故障诊断方法修正流程如图3所示。

图3 支持向量机的方法修正流程Fig.3 Correction process of support vector machine method

2 实验分析及结果

2.1 故障诊断结果分析

现以某种类型的三端口双向直流变换器为诊断对象，检测本文故障诊断方法对该直流变换器开关管故障诊断的有效性。在MATLAB/Simulink 软件环境中对其进行仿真实验，其中仿真拓扑如图1 所示，所用实验台如图4 所示，电路的关键参数见表2。为电感（变压器）的磁芯部分增添一个简单绕组，实现对电感（变压器）电压的衡量。在对信号进行预处理时，应设计恰当的信号放大电路与RC 滤波器，避免辅助绕组的电压存在高频纹波的可能。

图4 实验台Fig.4 Experimental bench

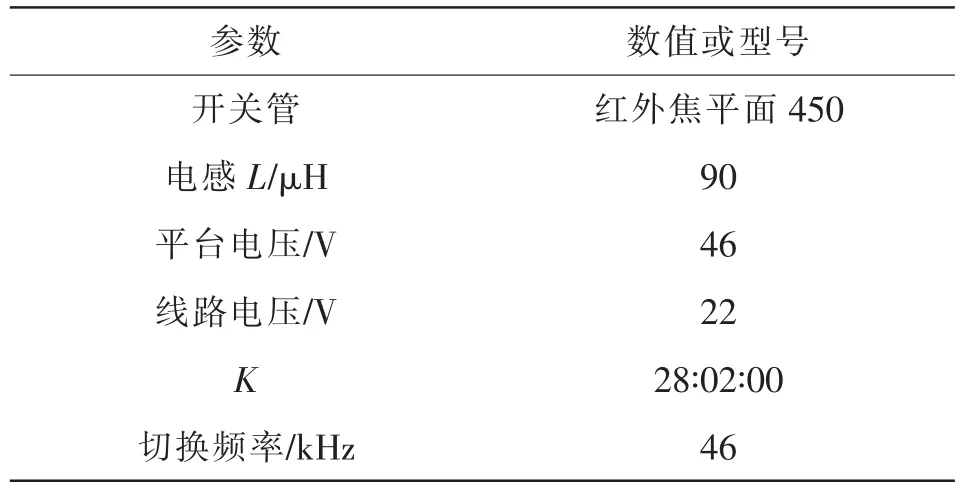
表2 实验台主要参数Tab.2 Main parameters of experimental bench

当三端口双向直流变换器工作于电流持续模式时，其开关管的断路故障由诊断电路负责诊断。实验中处于正常工作状态下的三端口双向直流变换电路器的电压um的时序如图5 所示。在以开关管的驱动信号P1直接对故障进行诊断时，因开关管的通断存在延时，造成诊断电路内M1r与M2r信号产生窄脉冲的问题，将导致诊断电路存在诊断误差，故应对驱动信号P1进行适当的延时，防止诊断误差的产生。

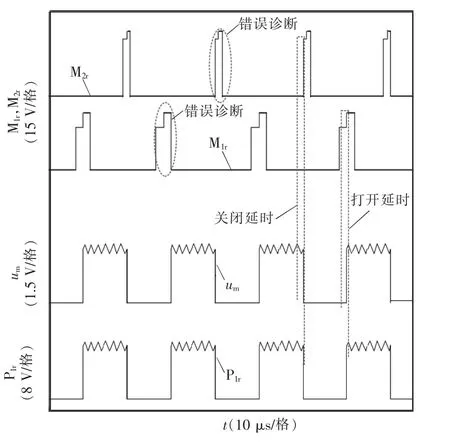
图5 延迟对实验波形的影响Fig.5 Influence of delay on experimental waveform

三端口双向直流变换器开关管的断路与短路故障的正确诊断结果如图6 所示。在开关管处并联一个0 Ω 电阻完成短路故障，将驱动信号消除后可得到开关管的断路故障。

图6 电路故障诊断实验波形Fig.6 Experimental waveforms during circuit fault diagnosis

通过图6 可看出，在三端口双向直流变换器处于正常工作状态时，其电压um和理论值非常接近，如图6（a）所示，电压um在三端口双向直流变换器开关管产生断路故障的状态下，在之后的一个开关时期内均为负；如图6（b）所示，电压um在开关管产生短路故障的状态下，在之后的一个开关时期内均为正。所以，故障指示信号MP1与MP2在诊断电路正常工作时，始终为高电平；如图6（a）所示，在开关管产生断路故障的状态下，只有M1r产生窄脉冲，MP1快速变成低电平；如图6（b）所示，在开关管产生短路故障的状态下，MP1仍然快速变成低电平，而产生窄脉冲的只有M2r。由此可说明，对三端口双向直流变换器的开关故障诊断可通过本文方法完成，且本文方法的诊断时间均在一个开关周期之内，诊断效率较高。

2.2 故障诊断性能分析

划分三端口双向直流变换器所处的SHEV 电气驱动系统中的IWBT 器件所出现的断路故障类型，具体为：①以W0表示器件处于正常运行情况下，此时仅有1 种情况；②以W1表示此时有1 个器件存在故障，分为6 种情况；③以W2表示同相的上下两臂中有2 个器件存在故障，如Q1、Q4，此时分为3 种情况；④以W3表示各相的2 个器件均存在故障，如Q1、Q6，此时共有12 种情况；⑤以W4表示有3 个或大于3 个的器件存在故障，此种情况在此不研究。

通过以上划分可得到22 组种数据，通过此类种数据对BP 神经网络的训练样本进行构造。

以20 Hz 的基波频率对故障的特点向量进行提取，在进行FFT 分析时，为各故障类别选择一些情况下的直流母线电流波形进行分析，依据分析结果可得出故障特点向量M=20 kHz 次谐波含量，由FFT分析所得的直流侧电流样本数据如表3 所示。

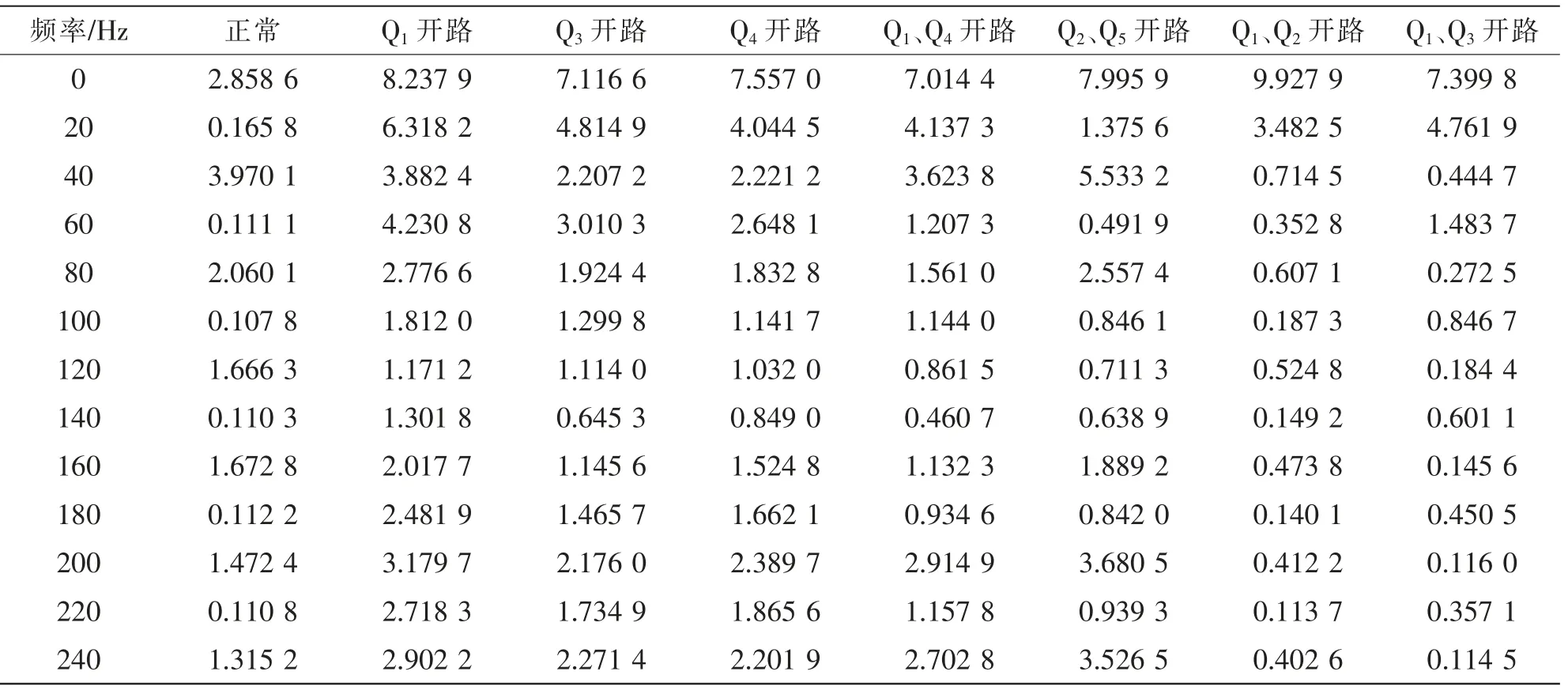
表3 不同故障状态的样本数据Tab.3 Sample data in different fault states

本文研究的4 种故障情况，其输出可分别表示为：①以W0（0，0）表示无故障情况；②以W1（0，1）表示仅有1 个器件发生故障的情况；③以W2（1，0）表示同相的2 个器件共同发生故障的情况；④以W3（1，1）表示不同相的2 个器件共同发生故障的情况。

为进一步检测训练后的网络，列出以下检测网络的测试数据，如表4 所示。

表4 试验样品数据Tab.4 Data of test samples

以上仿真实验样本的输入与输出参数分别为13、2 个，由此能够得出隐层神经元有27 个，故以13-27-2 设为神经网络的结构，那么权值与阈值分别有13×27+2×27=405 个、27+2=29 个，遗传算法优化后的参数数量是405+29=434 个。为令基于遗传算法优化的BP 神经网络故障诊断方法得以实现，须依据遗传算法与BP 神经网络的理论在MATLAB 软件中进行编程。其中，BP 神经网络应用MATLAB 自有的神经网络工具箱，遗传算法应用Sheffield 遗传算法工具箱。得出的运行结果为：优化之后的权值与阈值矩阵及预估结果的最低误差即为此算法的输出结果。通过遗传算法对BP 神经网络进行优化后，优化后网络的预估结果最低误差为0.033。

对比采用随机权值与阈值的检测样本所得预估结果和采用优化后权值与阈值的检测样本所得预估结果，具体对比数据见表5。

表5 预估结果对照Tab.5 Comparison between pre-estimated results

通过表5 可得，采用优化后权值与阈值的BP神经网络所得出的预估结果误差远低于采用随机权值与阈值所预估结果的误差。由此可见，在对三端口双向直流变换器电子电路所有器件的断路故障类型进行诊断时，采用以遗传算法优化的神经网络算法，能够提升诊断的准确性。

在诊断性能的诊断时间部分，通过对比随机权值与阈值的检测样本所得结果和采用优化后权值与阈值的检测样本所得结果，具体对比数据如表5所示。随机权值与阈值的检测样本所得诊断时间对比及优化后权值与阈值的检测样本所得诊断时间对比如图7、图8 所示。

图7 随机权值与阈值的检测样本所得诊断时间对比Fig.7 Comparison of diagnostic time based on detection samples with random weights and threshold

图8 优化后权值与阈值的检测样本所得诊断时间对比Fig.8 Comparison of diagnostic time based on detection samples with optimized weights and threshold

通过图7、图8 对比可得，采用优化后方法所得的诊断时间随着频率的增加呈现下降趋势，当频率都在180 Hz 时，Q6开路随机检测耗时在2.0 s 左右，而优化后的耗时在1.3 s 左右，Q3、Q6开路随机检测在1.6 s 左右，而优化后在1.2 s 左右，Q2、Q3开路随机检测耗时在1.4 s 左右，而优化后在1.0 s左右，Q3、Q5开路随机检测耗时在1.3 s 左右，而优化后耗时在0.7 s 左右，根据实验结果可知，采用优化检测法低于采用随机权值与阈值的诊断时间。由此可见，在对三端口双向直流变换器电子电路所有器件的断路故障类型进行诊断时，采用以遗传算法优化的神经网络算法，可以有效提升诊断时间。

3 讨论

在诊断三端口双向直流变换器的故障时，通过恰当的故障容错控制方法，对故障快速而有效地进行隔离，能够使变换器的可靠程度有较高的提升。对于当下诊断三端口双向直流变换器故障方法中所出现的缺陷，如诊断成本较高、时间过长及通用程度低等，本文在此提出一种全新的诊断故障方法。创建处于SHEV 电气系统内的三端口双向直流变换器仿真模型，以直流侧母线输出电流作为特点量，将功率器件的部位考虑到并合理划分各故障类别，研究每种故障对应的输出直流电流特点，向各频率段分解故障信号时通过FFT 实现，故障诊断特点向量为20 kHz 的频率段信号能量，对于故障类别的识别通过基于遗传算法的BP神经网络完成，依据仿真结果可得出：系统的故障特点信息能够通过三端口双向直流变换器的直流侧电流信号反馈，此信号和电压信号比较，不会产生谐波振荡等影响因素；BP 神经网络在经过遗传算法优化后，所得预估结果误差小且更精准。

由于当下所存在的三端口双向直流变换器大多是通过单管变换器变化得到的，且变换器内不能缺乏磁性元件，故可加大推行本文所提方法，同时这也是接下来需分析的问题。

4 结语

本文以三端口双向直流变换器为研究对象，探讨其断路故障的综合诊断方法。通过建立三端口双向直流变换器拓扑模型，并选取直流侧母线输出电流作为特点量，划分功率器件的不同故障类别并分析各故障输出电流特性，结合遗传算法BP 神经网络综合实现三端口双向直流变换器断路故障类型识别。且实验检测得出本文方法可准确有效地诊断三端口双向直流变换器的断路故障，降低其在新能源发电系统中使用时的故障发生率，及时隔离各部件故障，提升整个系统的安全运行能力，为促进现代微电子技术的飞速发展提供可靠依据。