一种基于四开关Buck-Boost 变换器的四模式控制策略

曹以龙，吴 丹，朱冬冬，江友华，杨兴武

（1.上海电力大学电子与信息工程学院，上海 200090；2.上海电力大学电气工程学院，上海 200090）

随着便携式电子设备的广泛使用，对电子设备电源部分要求也越来越高。电子设备需要适应不同大小的输入电压，以便对接各种设备[1-3]。四开关Buck-Boost FSBB（four-switch Buck-Boost）变换器因其可升、降压的突出能力，使其既适合便携式电子设备,也广泛用于电力系统、电池供电和功率因数校正器PFC（power factor corrector）电源。与传统的Buck-Boost 变换器相比，FSBB 电压应力更小，为了获得高效率，FSBB 变换器多采用两模式控制,即输出电压高于输入电压时工作在Buck 模式,反之工作于Boost 模式[4]。输入电压非常接近输出电压时，占空比接近于1，但由于开关管等电子元件不可避免的控制局限性，实际开关管的占空比无法达到1，导致FSBB 的电压转换比不连续，可能导致占空比紊乱，进而引起系统在Buck、Boost 模式间摇摆切换。将输入电压与输出电压非常接近的小范围称为盲区，盲区将导致变换器的输出电压纹波增大和电压失稳[5-6]。

文献[6-11]提出几种解决方案来缓解盲区问题。最简单的是以降低效率为代价，控制变换器在Buck-Boost 单模式下运行。文献[6]提出了一种复杂的补偿方法，需要对电源设备的运行性能细节进行精确测量，实际应用比较困难；文献[7]提出了一种三模双边缘调制方法，当输入电压达到预定的输出值附近时一个占空比被夹住在最大值，另一个占空比被控制调节输出电压，该方法中2 个占空比的极限不同，要求其下限值为0 才能完全消除盲区，但因为电子元件的实际限制，不可能达到；文献[10]提出了一种改进的占空比重叠控制方法，即重叠降压和升压模式的占空比，并设置合适的占空比限制，这种方法能消除脉冲跳变现象，实现模式的平滑过渡，但无法解决盲区问题；文献[11]提出了一种三模控制方法消除2 种模式间的波动，当变换器工作在Buck、Boost 模式时采用高频率，在缓冲模式时使用低频率。

为此，本文提出一种环路补偿的电压控制型四模式控制策略。通过分析输入、输出电压转换比与占空比的关系，推导出盲区产生原因，对传统控制策略加以改进，以彻底消除盲区影响。为更好地降低Boost 模式右半平面零点对整个工作电压范围的影响，在Boost 模式小信号模型基础上通过双极点双零点补偿电路改善控制环路，有效提升FSBB 变换器的整体性能和通过仿真和实验验证所提控制方法的正确性和有效性。

1 四开关Buck-Boost 变换器

四开关Buck-Boost 变换器如图1 所示。图中：开关管Q1、Q2构成Buck 单元，定义单元占空比d1；开关管Q3、Q4构成Boost 单元，定义单元占空比d2；L、C 分别为电感、电容，RL为电感寄生电阻，RC为电容等效串联电阻，R 为负载电阻；Vin为输入电压，Vout为输出电压。当RL、RC趋于0 时，由电感伏秒平衡原理得到电压增益无损表达式[12]为

图1 四开关Buck-Boost 变换器Fig.1 FSBB converter

由式（1）可以看出，FSBB 变换器的电压增益仅与d1、d2有关，且两者互不影响。占空比取值恒小于等于1，因此当占空比d2取值趋近于0 时，FSBB 变换器等效于Buck 变换器；当占空比d1取值趋近于1时，FSBB 变换器等效于Boost 变换器。

2 FSBB 控制策略

研究表明，FSBB 变换器的双模调制策略，即在输入电压高于输出电压时变换器工作在Buck 模式，反之则工作在Boost 模式，可以显著提高变换器的整体效率，但这种调制策略也存在一个不容忽视的缺点。由于实际中非理想性电子元器件、开关噪声以及电路布局等不可避免的影响和干扰，占空比总是有一个上限值dmax和一个下限值dmin，因此，1-d1和d2只能实现区间[dmin，dmax]范围值，两模式盲区示意如图2 所示，这表明电压转换比Vout/Vin只能在电压范围[Vin_min，Vmid_1]、[Vmid_2，Vin_max]取值，而区间[0，Vin_max]、[Vmid_1，Vmid_2]和[Vin_min，∞]则无法取到。为了实现电压转换的连续性，无法忽略[Vmid_1，Vmid_2]的范围，而由于占空比的局限，此范围无法直接得到。因此，将其定义为盲区，如图2 阴影区域。

图2 两模式盲区示意Fig.2 Schematic of blind area in two modes

为了消除盲区，需要取得[Vmid_1，Vmid_2]区间的输入输出电压转换比，这意味着需要在双模调制方案中插入其他的工作模式。因此，通过插入过渡模式来实现Buck 模式和Boost 模式的平滑变换。

2.1 四模式控制原理

为解决上述问题，本文提出一种四模式控制方案，在FSBB 变换器拓扑的基础上，采用带补偿电压反馈的四模式切换控制策略，图3 给出了所采用系统的整体结构，在不同模式下给电压控制器不同的电压参考Vref，通过输入电压与参考电压Vref的大小来判断进入哪种工作模式，与Vref比较得到误差电压E（s），然后经过补偿校正环路得到控制信号Vc（s），再与锯齿波信号比较产生对应的PWM 信号来控制d1、d2，从而改变输出电压。

图3 系统整体控制框图Fig.3 Control block diagram of the whole system

FSBB 的工作模式与占空比范围如表1 所示。结合表1，可以得到4 种模式的切换过程。

表1 FSBB 的工作模式与占空比范围Tab.1 Working modes of FSBB converter and the corresponding duty cycle range

图3 中，Vclamp1为Buck 模式的电压最小值，Vclamp2为Boost 模式的电压最大值，设置占空比的最小值dx1和最大 值dx2。则当Vin大于Vclamp1时，为Buck 降压模式，此时只有一对开关管工作，占空比取值d1=Vout/Vin，d2=0，Vout保持不变，Vin减小，则占空比d1的值增大；当输入电压Vin减小至低于Vclamp1但高于Vout时，切换至E-Buck 模式，此时2 对开关管均处于工作状态，由占空比d1=Vout（1-dx1）/Vin调节输出，占空比d2取固定值dx1，可以保证d1的取值肯定小于1，避免进入盲区；当Vin继续减小至低于Vout但高于Vclamp2时，切换至E-Boost 模式，此时2 对开关管均处于工作状态，占空比d1取固定值1-dx2，由占空比d2=1-Vindx2/Vout调节输出，保证了2组占空比均在极限值范围内，不会进入盲区；当Vin继续减小至低于Vclamp2时，切换至Boost 升压模式，此时只有1 对开关管工作，占空比取值d1=1，d2=1-Vin/Vout。

2.2 系统设计

图4 为FSBB 变换器闭环控制框图，图中，GVout_Vin（s）为变换器Vin到Vout的传递函数，H（s）为输出电压采样系数，Gc（s）为输出电压调节器传递函数，Gm（s）为PWM 调制器传递函数，Gvd（s）为控制到输出电压传递函数。

图4 FSBB 的电压闭环控制框图Fig.4 Voltage closed-loop control block diagram of FSBB converter

根据文献[13]所述建模方法，得到图5 所示的FSBB 变换器的小信号交流模型。由此推导出Buck工作模式下变换器控制-输出的传递函数Gvd_buck（s）为

图5 FSBB 变换器小信号交流模型Fig.5 Small signal AC model of FSBB converter

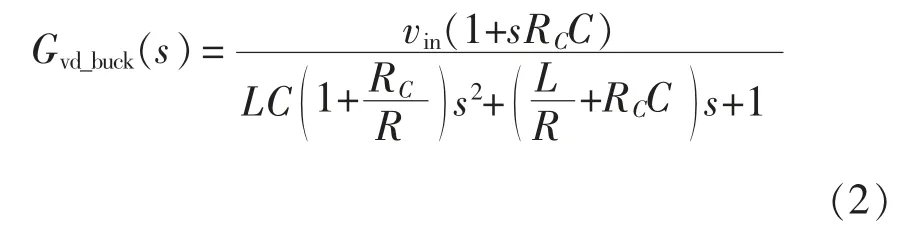
Boost 模式下变换器控制-输出的传递函数Gvd_boost（s）为

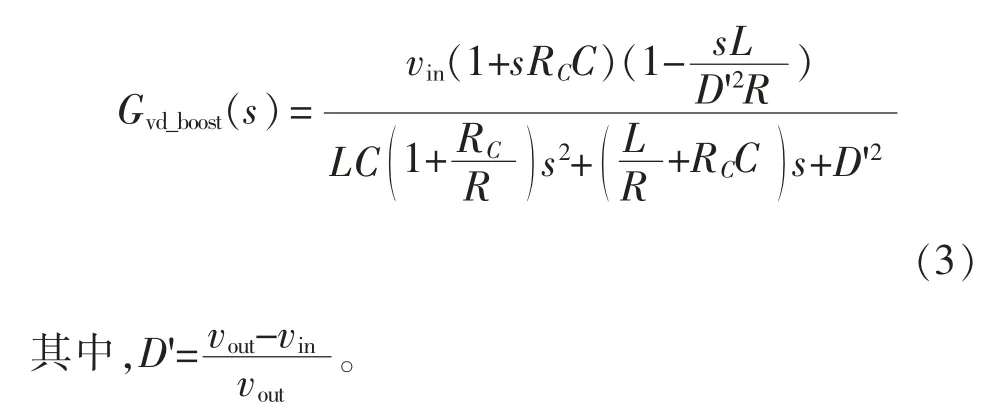
2.3 控制设计

由式（3）可知，Boost 模式下电压环路增益函数比Buck 模式多了一个右半平面RHP（right half plane）零点，该零点频率为

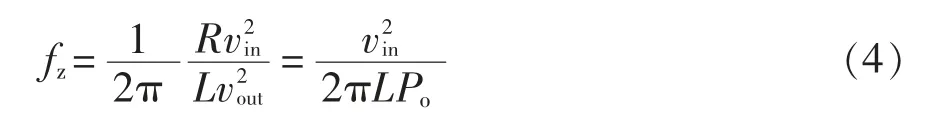
式中，Po为输出功率。采用PID 调节器来提高低频增益和动态响应速度，当负载增大时，RHP 零点频率降低，在设计电压环时需要保证环路增益的截止频率低于RHP 零点频率的最小值[13-14]。而对于Buck模式没有这一限制，因此补偿网络按Boost 模式设计。实际工作中在Boost 模式输入电压最小并且满载时达到最低频率，因此将这一值作为截止频率可以达到的最大值。根据给定参数，输入电压最小为3 V，电感L 为20 μH，满载输出功率Po为12 W，代入式（4）可得fz=5.97 kHz。通常截止频率选为RHP 频率值的1/2～1/4，所以选择截止频率fo=2.98 kHz。

补偿网络的2 个极点，其中，第1 个用于消除ESR 零点，；第2 个用于抑制高频噪声，选为fc的10 倍，即fp2=10fc=40 kHz。因此补偿网络公式为

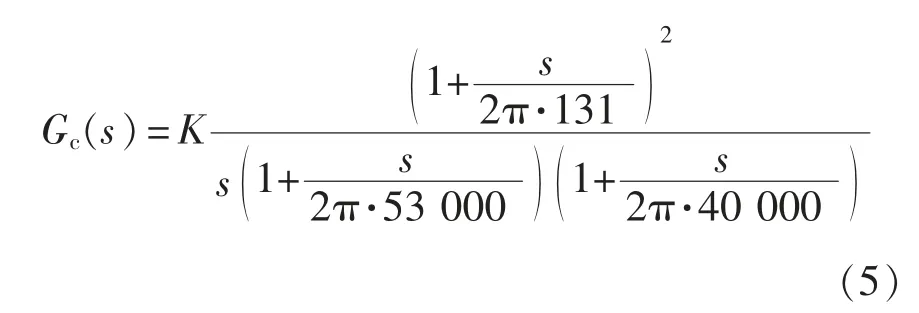
式中，K 为补偿网络的增益。预校正后系统的开环传递函数Gc（s）G0（s）|K=1在穿越频率fc处的增益为-A，为使补偿后Gc（s）G0（s）在穿越频率fc处的增益等于0，则K 取值为

补偿后Boost 和Buck 开环传递函数Bode 图如图6 所示。图6（a）给出补偿后的系统开环传递函数的Bode 图，可见此时穿越频率4 kHz，且当f=4 kHz时，PID 补偿网络增益K=1 时对应的开环对数幅值为-17.2 dB，代入式（6）可以求得K=108.4，再将K值代入式（5）；图6（b）给出了K=108.4 补偿后的系统Boost 开环传递函数的Bode 图，可见校正后穿越频率为4 kHz，相位裕度为80°；图6（c）给出了补偿后的Buck 开环传递函数的Bode 图，校正后穿越频率为4 kHz，相位裕度为84°，系统稳定。

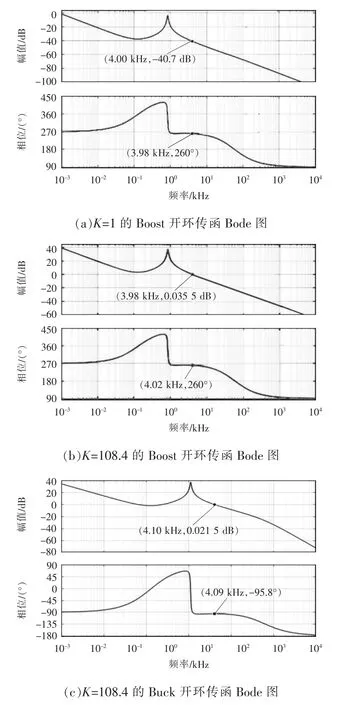
图6 补偿后Boost 和Buck 开环传函Bode 图Fig.6 Bode diagrams of compensated Boost and Buck open-loop transfer functions

3 实验结果

四开关Buck-Boost 硬件平台如图7 所示，为了验证所提控制策略的正确性和有效性，搭建了一台实验样机，电路的参数如表2 所示。根据前文分析，设置极限占空比[dx1，dx2]=[0.1，0.9]。

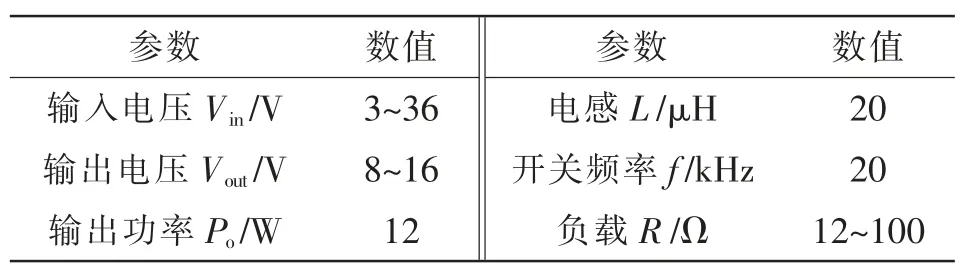
表2 样机参数Tab.2 Parameters of prototype

图7 四开关Buck-Boost 硬件平台Fig.7 FSBB hardware platform

图8 为4 种控制模式下的2 组占空比波形，可以看出实验波形与理论基本一致。

图8 不同模式下的占空比波形Fig.8 Waveforms of duty cycle in different modes

图9 展示了负载不变的情况下，输入电压5、11、13、20 V 情况下对应的4 种控制模式的输出电压、电感电流的实验波形。

图9 不同模式下的输出电压和电感电流实验波形Fig.9 Experiment waveforms of output voltage and inductor current in different modes

为了验证所提出的四模式控制策略的动态性能，又进行了一些输入电压和负载条件突变的实验，具体实验结果如图10 和图11 所示。图10 显示了当负载保持不变仅有输入电压变化时，输出电压的实验波形。可以看出，切换过程中没有出现大的波动，输出电压稳定，模式切换的瞬态响应性能也比较令人满意。图11 显示了4 种控制模式下负载突然变化时对应的输出电压和输出电流的实验波形。可以看出，随着负载的变化，输出电压基本保持稳定，系统带负载能力较好。当输入电压增大时，纹波也略有增大，这是由于输入源的内部电阻引起的。

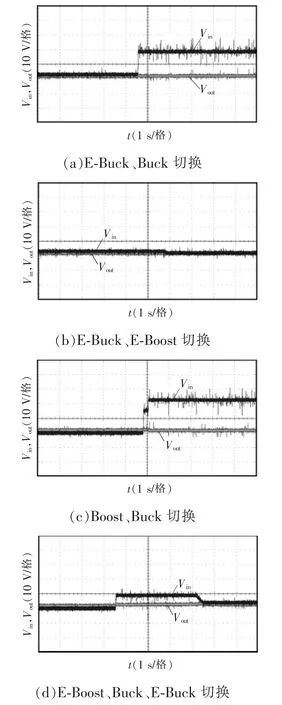
图10 不同模式切换的电压实验波形Fig.10 Experiment waveforms of voltage during switching between different modes

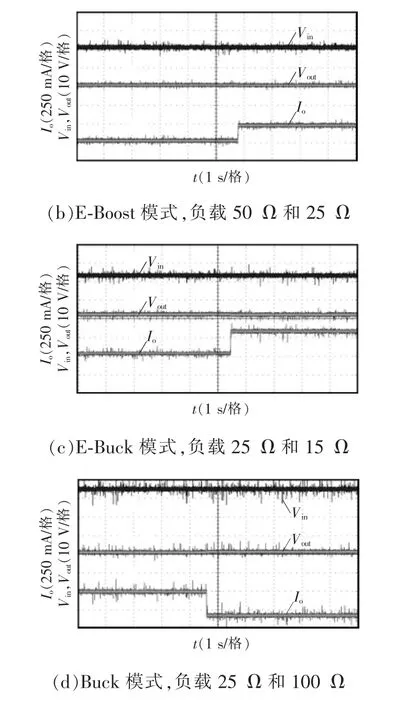
图11 不同模式下负载改变的实验波形Fig.11 Experiment waveforms under load changes in different modes

实验结果很好地证明了本文所提四模式控制策略的正确性和有效性。

4 结论

为了解决四开关Buck-Boost 变换器的两模式控制策略不能解决输入输出电压接近时模式频繁切换以及盲区的问题，本文提出了一种带环路补偿的电压控制的四模式控制策略，仿真及实验结果表明：

（1）所提的控制策略能够有效解决双模控制方案存在的盲区问题，使系统获得更好的整体性能。

（2）FSBB 系统能在提出的带补偿的四模式控制策略下平稳运行，补偿参数合理，系统响应迅速。