基于补偿网络电流分析的恒压恒流无线充电系统

李 乐，程 冰，何良宗，刘厚轩

（厦门大学仪器与电气系，厦门 361102）

在民用航空运输中，通常会在机舱内配备娱乐电子设备，使用传统的有线方式进行供电在插拔过程中会存在冒电火花的风险，同时便利性不足。对此，本文采用无线电能传输WPT（wireless power transfer）的方式对其进行供电，与传统有线传输电能的方式相比，WPT 具有更加安全、可靠和便捷的优势[1]。另外，大多数电子设备都是由锂电池进行供电，而锂电池充电过程包含恒流CC（constant-current）充电和恒压CV（constant-voltage）充电两个阶段[2]，故实现恒压恒流的无线充电技术引起了广泛的关注。

目前研究人员已经提出了许多不同的方法来实现恒流恒压输出。在文献[3-4]中，利用谐振腔网络在特定频率点具有恒压或恒流输出的传输特性，通过调节开关频率可实现恒流恒压模式之间的切换，但开关频率切换的时机需要原副边之间无线通信，这会增加系统控制复杂度，在恒压或恒流模式下不能实现输入零相角，会带来较大的无功功率[5]。文献[6]通过移相控制调节逆变器的输出电压，进而保证整个充电过程中的恒流恒压输出要求，但移相控制会导致逆变器中开关管的软开关丧失,进而降低整个系统的传输效率。文献[7-9]在原边侧或副边侧增加一个DC-DC 变换器，通过检测输出电压或电流来调节DC-DC 变换器的占空比，进而实现恒流恒压输出，然而额外级联的变换器不仅会增加充电系统的体积和成本，还会引入额外的损耗降低系统传输效率。相比之下，文献[10-11]通过切换辅助开关重构补偿网络结构的方法来实现系统的恒流恒压模式切换，其不需要额外的电路以及复杂的控制电路。然而现有的补偿网络在参数设计过程中并未考虑回路电流应力的影响，这会导致在输出功率较高时，系统中各回路电流过大，系统损耗增加，严重时甚至会损坏开关器件进而影响整个传输系统的稳定性。

针对上述提到的问题，本文首先从二阶补偿网络出发，推导出回路电流压力最低的条件，并进一步推广到高阶补偿网络，得到高阶补偿网络中各回路电流应力最低条件，解决了回路电流应力过大的问题。其次，基于完全对称补偿网络结构和T 型网络结构，阐述了负载无关恒压恒流输出的机理，得到一系列负载无关恒压恒流输出混合拓扑。接下来，基于所提出的一组恒压恒流混合拓扑，结合回路电流应力最低的条件来设计混合拓扑参数，从而确保实现恒压恒流输出的同时使得拓扑中各回路的电流应力最低。此外，其恒流恒压模式的切换仅通过检测原边电流就能实现，避免了原副边之间的无线通信问题，大大简化了控制电路。最后，本文搭建了恒流输出为5 A、恒压输出为96 V 的实验样机，实验结果验证了所述方法的有效性。

1 高阶网络的回路电流应力与效率分析

1.1 低阶网络的电流应力和效率分析

高阶网络可以看作是多个低阶网络级联而成。因此，本文先分析低阶网络的回路电流应力和效率特性。

图1 为电压源型低阶网络，其中Vin为交流电压源，Rsm、Rs（m+1）为相应支路的寄生电阻，Im、Im+1分别为相应支路的电流，Zsm、Zpm、Zs（m+1）分 别代表相应 支路无源元件的等效阻抗，ZL为负载的等效阻抗。为了简化分析，先忽略相应支路的寄生电阻。

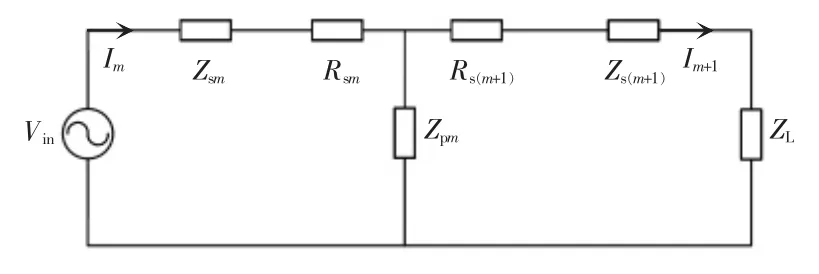
图1 电压源型低阶网络Fig.1 Low-order network fed by voltage source

根据基尔霍夫定律可知

因此，Im的表达式为

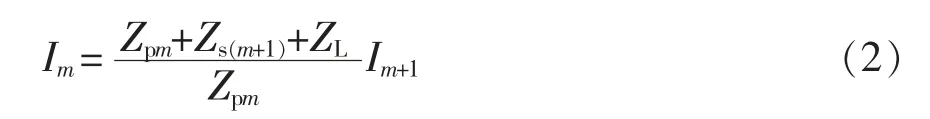
当Zpm、Zs（m+1）和ZL满足

时，电流Im的虚部为0，电流Im最小。此时，Im的表达式可简化为

同时输出功率Po的表达式为

当输出功率Po恒定时，系统的传输效率为

由式（4）、式（6）可知，当输出功率Po恒定，同时满足条件（3）时电流Im只与参数Zpm有关。因此，当Zpm越大时，回路电流Im越小，寄生电阻Rsm上的损耗更小，系统的传输效率。

1.2 高阶网络的电流应力和效率分析

高阶网络如图2 所示，其中Vin为交流电压源；Rs1，Rs2，…，Rsn分别为相应支路的寄生电阻；I1，I2，…，In分别为相应支路的电流；Zs1，Zs2，…，Zsn分别表示串联无源元件的阻抗；Zp1，Zp2，…，Zp（n-1）分别表示并联无源元件的阻抗；ZL为负载的等效阻抗。

图2 电压源型高阶谐振网络Fig.2 High-order resonant network fed by voltage source

从低阶网络得到的条件式（3）递推可知，当高阶网络中的参数满足

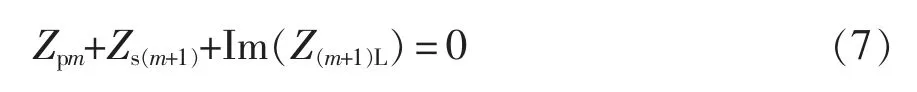
各支路电流I1，I2，…，In-1达到最小值，表达式为

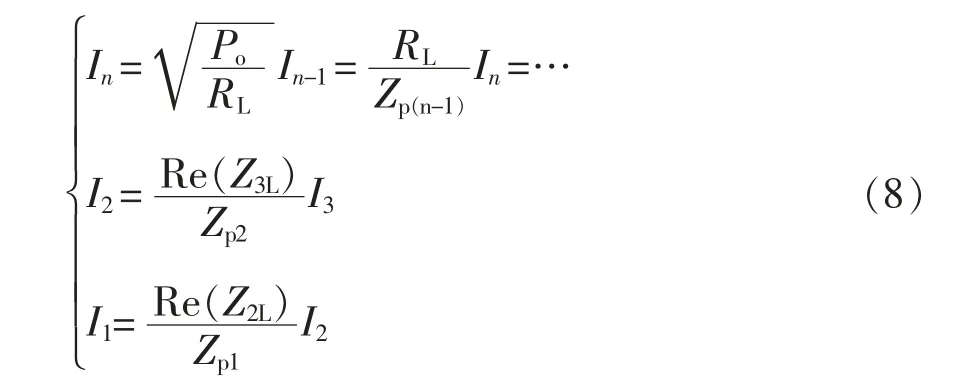
高阶网络的传输效率为

高阶网络各支路的电流应力与各个并联支路Zpm有关。当使用的网络中包含2 个以上的Zpm时，可以通过条件式（7）进行参数优化，使得支路的电流应力减小，各支路的能量损耗降低，来提高高阶网络的传输效率。

2 负载无关输出的补偿网络核心机理与拓扑推演

2.1 完全对称补偿网络的传输特性

对于一个完全对称的补偿网络来说，如果恒压源输入能实现负载无关的恒流输出，那么恒流源输入就能够实现负载无关的恒压输出。为了更具体地介绍该特性，本文以结构最简单的SS 补偿网络为例，如图3 所示。图3（a）是电压源型SS 补偿网络，由基尔霍夫定律可得

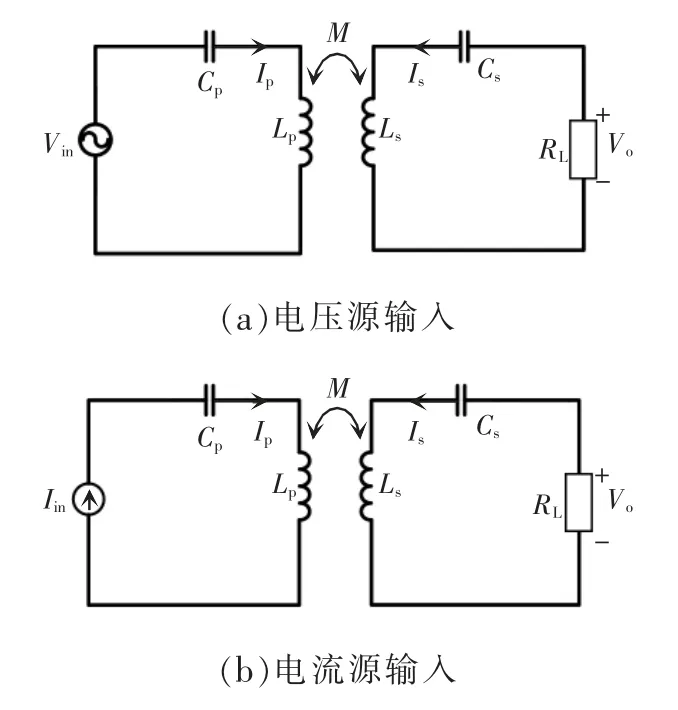
图3 基于S/S 补偿的基本电路Fig.3 Basic circuits based on S/S compensation

最大耦合效率ηcoilmax和负载无关输出的条件为

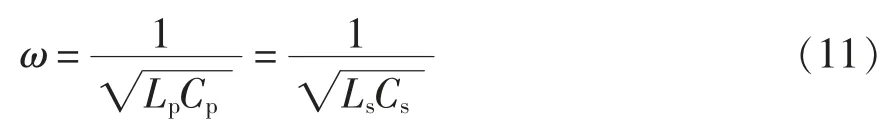
由式（10）、式（11）可得Is的表达式为

由式（12）可知，电压源型SS 型补偿网络能够实现负载无关的电流输出。

图3（b）是电流源型SS 型补偿网络，其中Iin为交流电流源。当该补偿网络满足条件式（11）时，其输出电压的表达式为

因此，电流源型SS 型补偿网络能够实现负载无关的电压输出。

通过对SS 补偿网络的分析，可以确定原副边完全对称网络具有恒压源恒流源相互转换的传输特性。除了SS 补偿网络，PP 补偿网络[12]、双边LCC补偿网络[13]均有该传输特性。

2.2 恒压恒流输出模式切换的核心机理

由上述分析可知，完全对称的补偿网络（CN1）在不同输入源的形式（即电压源或电流源）下，可实现负载无关的恒流或恒压输出。在此基础上，可通过补偿网络（CN2）来实现电压源和电流源之间的相互转换以及恒压恒流模式切换。

2 种最简单的CN2 结构分别为T 型网络和π型网络，如图4 所示。其中V1和I1可以看作是输入源，V2和I2可以看作是所需的输出源，Z1、Z2、Z3是二端口网络的3 个无源元件。本文以T 型网络为例进行分析。

图4 CN2 的两种最简结构Fig.4 Two simplest structures of CN2

根据基尔霍夫定律可知，输入电压V1、输出电压V2分别为

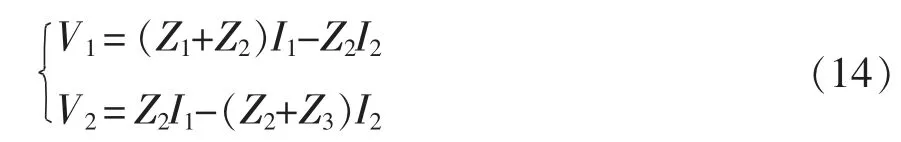
由式（14）可得，V2、I2的矩阵形式表示为

因此，当输入电压V1恒定时，恒流输出和恒压输出的条件分别为

此时恒流输出电流I2和恒压输出电压V2可简化为

类似地，当输入电流I1恒定时，恒流输出和恒压输出的条件分别为

此时恒流输出电流I2和恒压输出电压V2简化为

由上述分析可知，可以通过T 型网络来实现恒压源和恒流源的相互转换。

基于上述分析，设计了如图5 所示的2 种混合拓扑，共用参数在图5 中突出显示。恒压恒流模式可以在所提出的混合拓扑中灵活切换。

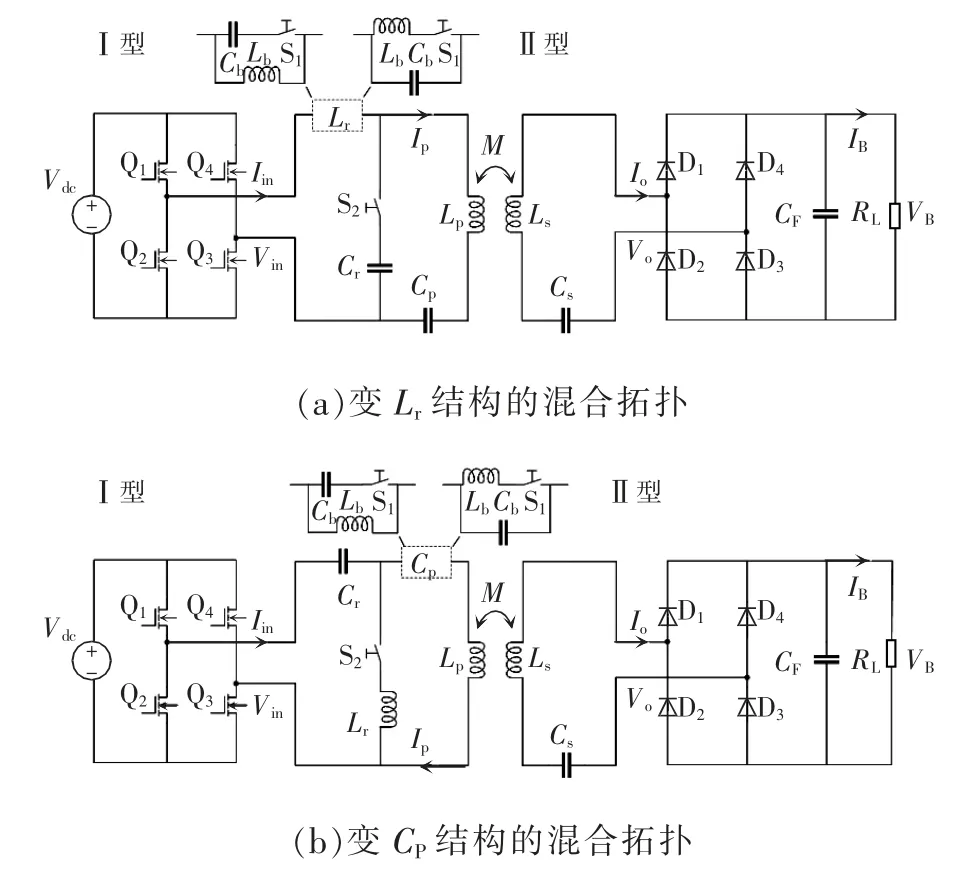
图5 实现恒压恒流输出的混合拓扑Fig.5 Hybrid topologies to realize constant-voltage and constant-current output

3 所述拓扑恒压/恒流模态分析

3.1 所述拓扑恒流模态下分析

本文采用图5（a）中I 型三阶混合拓扑为例进行分析，恒压恒流模态的等效电路如图6 所示。

图6 恒压、恒流模态的等效电路Fig.6 Equivalent circuit in constant-voltage or constant-current mode

当开关S1开通，开关S2关断，系统工作在恒流模态下，等效电路如图6（a）所示，负载无关恒流输出条件为

设流过等效电阻Req上的电流Io与输入电压Vin的模值之比为GUI，则系统的电流增益GUI为

同时，系统的输入阻抗ZUI为

由于输出电流Io恒定，根据KVL 方程可得，原边输入电流Iin为

该系统的传输效率为

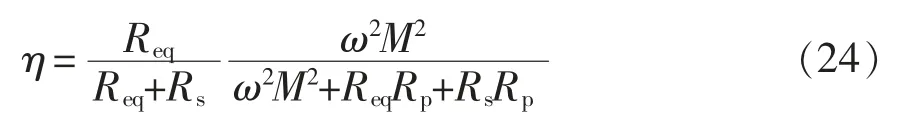
由式（23）和式（24）可知，增大互感M 和工作频率ω 能够降低回路电流应力并提高系统传输效率。

3.2 所述拓扑恒压模态分析

当开关S1关断、开关S2开通时，系统进入恒压模态，等效电路如图6（b）所示，恒压输出的条件为

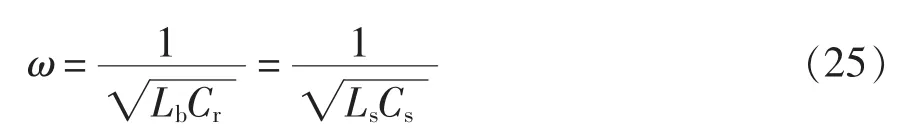
设等效电阻Req两端的电压Vo与输入电压Vin之比为GUU，则电压增益GUU为

同时，系统的输入阻抗ZUU为

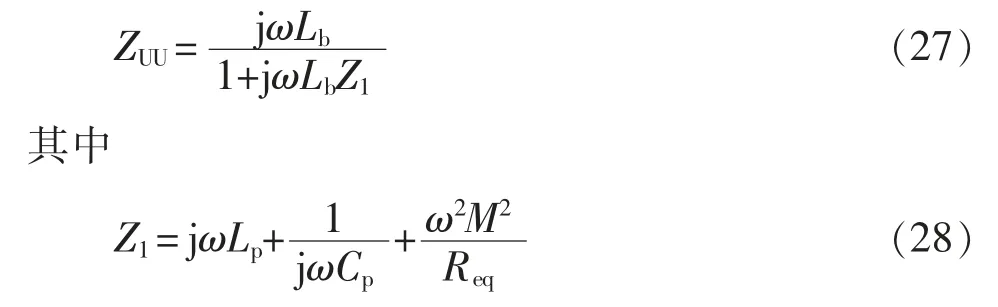
根据欧姆定律和电路理论可知，各个回路电流表达式分别为

若使得Iin最小，可通过式（7）进行优化。优化后电流Iinopt为

恒压模态系统的传输效率为

4 参数设计和控制策略

4.1 参数设计

由上述分析可知，本文所提出的恒压恒流输出拓扑能够通过重构补偿网络，使其在恒定工作频率下实现所需的恒压和恒流输出，同时也能实现ZPA。本文所提拓扑的参数设计流程如图7 所示，为了简化设计过程，首先分析一些基本的等效关系。

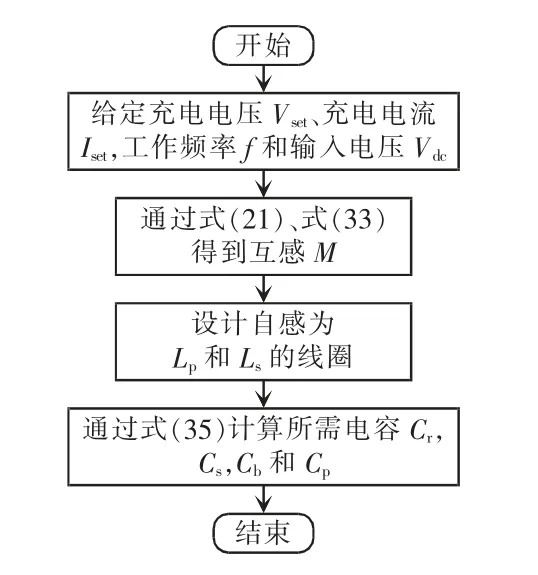
图7 参数设计流程Fig.7 Flow chart of parameter design

采用H 桥逆变器产生所需工作频率的方波，则输出电压的基波有效值与直流电压Vdc的关系为

整流桥前端电压电流与电池充电所需的额定电压和额定电流的关系为

这些断层在各期次活动中不断发生变化，相互切割交错，在交汇处形成复杂的断裂组合，控制形成潜山、洼陷、隆洼相间的构造样式。

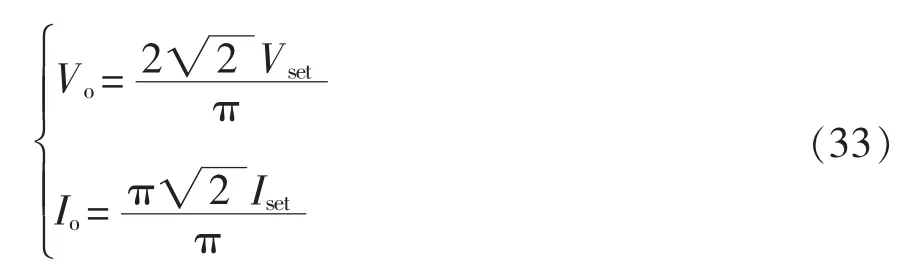
同时根据不同的参数来设计恒流模式下的充电电流Iset和恒压模式下的充电电压Vset。通过式（21）、式（26）、式（33）可得松耦合线圈的互感M，即

根据恒流输出条件式（20）、恒压输出条件式（25）、和电流优化条件式（7）可得，电容Cr、Cp、Cb和Cs分别为

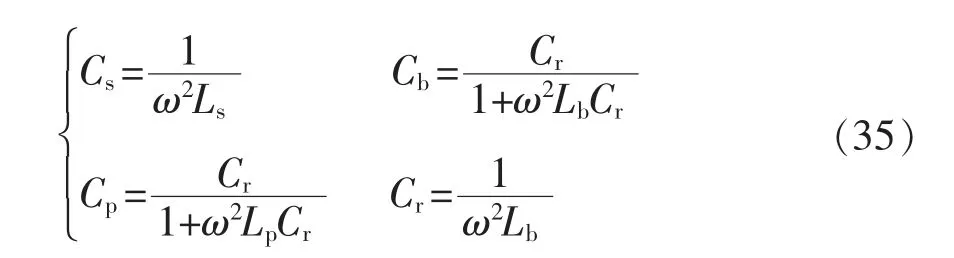
4.2 控制策略

为了估计恒流模态向恒压模态转变的临界点，根据能量守恒定理，推导了充电电压VB和原边谐振网络电流Ip的关系，即

通过式（36）可得Ip的有效值为

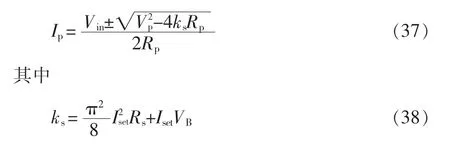
恒压恒流模式下电流Ip与充电时间t 的关系如图8（a）所示，在恒流模式下，Ip会随着VB增大而增大，当电压VB 达到预设电压Vset时，电流Ip也会达到Ipset，此时开关S1断开，开关S2开通，系统进入恒压模式，输出电压VB等于Vset。恒压恒流模式的控制框图如图8（b）所示。

图8 无线能量传输系统恒压恒流切换策略Fig.8 Constant-voltage and constant-current switching strategy for wireless power transfer system

根据KVL 方程可得，恒压模式下Ip与RB的关系为

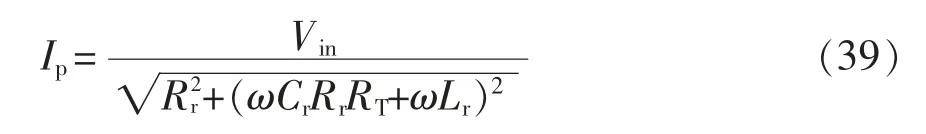
式中，RT为副边等效到原边的阻抗，其表达式为

因此，可以通过检测原边电流Ip来进行恒流模式向恒压模式的切换，而不需要检测负载阻抗及双边通信来确定模式的切换点。

5 实验结果

5.1 实验平台

为了验证上述分析的可行性，本文搭建了如图5（a）所示I 型实验样机。实验样机的最大输出功率为480 W,线圈间距为15 cm，其实验平台如图9所示，实验参数如表1 所示。

表1 所述无线电能传输系统实验参数Tab.1 Experimental parameters for proposed wireless power transfer system

图9 实验平台Fig.9 Experimental platform

5.2 实验结果

刚开始充电时，系统处于恒流模式。负载为5 Ω和10 Ω 时的输出电压VB、输出电流IB、全桥逆变器的输入电压Vin和输入电流iin的波形如图10 所示。从图10（a）、图10（b）中可以看出，在工作频率85 kHz下，输出电流等于预设电流5 A，逆变器的各开关均实现了ZVS 和近似ZPA。为了测试所述系统在负载变化的稳定性，负载变化的瞬态响应曲线如图10（c）所示，可以看出，当负载由5 Ω 变化到10 Ω 时，电流经过短暂的波动后依然维持在5 A，此时电压从25.06 V 变化到50.15 V。

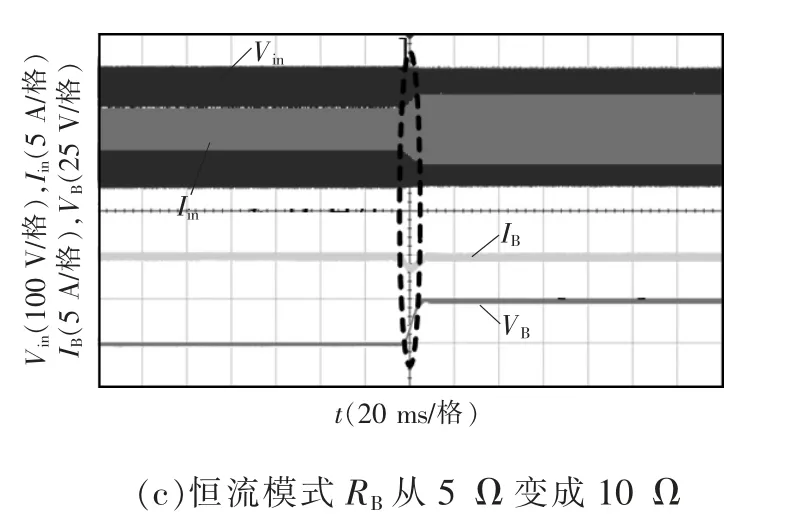
图10 恒流模式当RB 为5 Ω 和10 Ω 以及5 Ω 变为10 Ω 时，Vin,Iin,VB,IB 的波形Fig.10 Waveforms of Vin,Iin,VB,and IB in constantcurrent mode when RB equals 5 Ω or 10 Ω and when it changes from 5 Ω to 10 Ω

系统处于恒压模态时，输入电压Vin、输入电流Iin、充电电流IB和充电电压VB在负载为35 Ω 和70 Ω 下的主要波形如图11 所示。从图11（a）、图11（b）可以看出，电压能够维持在96 V 不变，同时，逆变器的开关也实现了ZVS 与近似ZPA。为了测试无线电能传输系统在恒压模式下的动态性能，负载突变的测试结果如图11（c）所示。当负载从35 Ω变为70 Ω 时，充电电压经过一个小的波动依旧稳定在在96 V；而充电电流从2.74 A 下降为1.28 A，证明了该无线充电系统具有优良的恒压特性。

图11 恒压模式当RB 为35 Ω 和70 Ω 以及35 Ω 变为70 Ω 时，Vin，Iin，VB，IB 的波形Fig.11 Waveforms of Vin,Iin,VB,and IB in constantvoltage mode when RB equals 35 Ω or 70 Ω and when it changes from 35 Ω to 70 Ω

模式切换的瞬态波形如图12 所示，从图12 可以看出，通过切换两个额外的开关的工作状态，系统能够平滑地从恒流模式切换到恒压模式。另外两个额外开关的驱动信号如图12（b）所示，可以看出，当S1开通，S2关断，系统处于恒流模式；当S1关断，S2开通时，系统进入恒压模式。整个过程不存在电压或者电流尖峰，证明了系统在模式切换时良好的安全性能。

图12 恒流模态切换为恒压模态时，Vin、Iin、VB、IB、S1、S2 的波形Fig.12 Waveforms of Vin,Iin,VB,IB,S1 and S2 when constant-current mode is switched to constant-voltage mode

优化前的拓扑如图13 所示，参数如表2 所示。当S1开通、S2断开时，系统处于恒流模式；S1断开、S2开通时，系统处于恒压模式。优化前后的电流Iin与负载的关系如图14 所示。Iin的测量值与计算值的差异是由于设计电感电容的参数与实际使用的电感电容的参数存在一些偏差造成的。从图14 可以看出，在系统输出相同功率时，根据本文所述的回路电流优化方法进行参数优化，能有效地减小回路中的电流。

图13 优化前的拓扑Fig.13 Topology before optimization

表2 优化前的参数Tab.2 Parameters before optimization

图14 恒压模态下输入电流Iin 与负载R 的关系曲线Fig.14 Curves of Iin vs R in constant-voltage mode

图15（a）为充电过程中充电电流和充电电压的变化曲线。恒流模式下的电流与恒压模式下的电压的微小偏差主要是由无源元件的寄生电阻和实际电感电容的误差引起的。优化后的充电效率曲线如图15（b）所示，恒流模式下效率从73.6%上升到90.8%，其中损耗主要发生在接收侧。系统为恒压输出时，电池电阻增大，输出电流逐渐减小，传输效率在输出功率为184.4 W 时达到最大值95.4%，之后下降到92.1%。由图15（b）的恒压模式下未经优化时的效率曲线可见，随着充电过程的进行，它的输入阻抗角会增加，因此发射端的功率损耗会越来越大，电池充电效率下降了36%，表明本文所述的回路电流优化方法能够有效地提高系统的传输效率。

图15 系统充电曲线和效率曲线Fig.15 Charging and efficiency curves of system

6 结语

本文首先通过对低阶网络和高阶网络回路电流进行分析，得到了回路电流最小的条件。其次，通过对完全对称结构进行分析，得到了一系列满足负载无关恒压恒流输出的拓扑，并结合回路电流最小的条件对恒压恒流系统进行参数设计。此外，通过检测原边侧谐振电流进行充电模式切换，避免原副边通信。实验结果表明，该拓扑在恒压恒流模式切换及负载变化的情况下都能保持稳定的输出，并且恒压恒流模式下均能实现ZPA，同时充电效率最高可达95.4%，相比未优化前，本文所提拓扑的充电效率最高可以提高36%。