高拱坝抗震安全评价指标研究——以白鹤滩拱坝为例

秦礼君，陈健云，2，徐 强，李 静

(1.大连理工大学 工程抗震研究所，辽宁 大连 116024；2.大连理工大学 海岸与近海工程国家重点实验室，辽宁 大连 116024)

1 研究背景

拱坝因其具有经济合理、安全可靠的优点，在世界范围内被广泛使用。在水力资源丰富的我国西南部，有一系列特高拱坝已落成或正在建设之中，但同时，这部分地区也是我国高地震烈度区。大坝作为水利工程的核心主体建筑物，其安全性是整个工程的关键[1]。一旦强震导致拱坝坝体破坏，将造成不可估量的生命与财产损失。因此了解拱坝在地震作用下的破坏模式、对拱坝进行抗震安全评价是一项重要研究课题。

为了探究混凝土拱坝在强震作用下的破坏模式及薄弱部位，许多学者开展了振动台试验及有限元仿真试验。杜荣强等[2]对大岗山拱坝和溪洛渡拱坝进行强震破损分析和比较，计算结果表明上游面拱冠梁上部是抗震薄弱部位。张宇等进行的振动台破坏试验中[3-4]，考虑拱坝-库水相互作用时，顶拱拱冠处及拱冠梁位置发生了中等或严重损伤；不考虑库水影响时，模型进入悬臂梁破坏模式后顶拱拱冠为抗震薄弱环节。周光平[5]的研究中，拱坝下游面在震动中出现拱向裂缝，超载结束后已经上下游贯穿。邹浩[6]的高拱坝振动台试验中，在地震动逐级加载过程中拱坝中上部的上下游面都出现了拱向宏观裂缝。范书立等[7]学者在试验中发现在强震的作用下，顶拱的中部是坝体的薄弱部位，拱向裂缝和梁向裂缝贯穿上下游后，将造成混凝土块从坝体上脱落(如图1所示)。

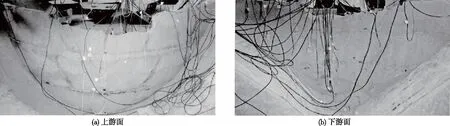
图1 高拱坝振动台试验坝体破坏形态[7]

振动台试验结果及数值仿真结果说明，拱坝的中上部为抗震薄弱部位，在强震作用下产生较大的损伤，很可能出现宏观水平裂缝，并在持续的振动中进一步扩展，最终造成水平裂缝的上下游贯穿。在库水与地震的同时作用下，坝体中上部的混凝土块体可能沿着裂缝面滑动或倾倒，导致混凝土块体脱离坝体，使拱坝失去挡水作用。拱坝的挡水部分如果遭到破坏，倾泻而下的洪水必将对下游造成灾难性的后果。因此，高拱坝中上部的抗震安全应当引起重视，选用合适的指标对高拱坝中上部的局部损伤状态进行评价、对高拱坝中上部易破损位置进行定位设防具有重要意义。

目前已有许多学者进行了高拱坝抗震安全评价方法的研究，针对高拱坝的局部损伤或拱坝-地基整体系统提出了安全评价指标，探讨了高拱坝的抗震稳定性。涂劲等[8-10]采用强震时坝体位移反应发生突变作为拱坝体系整体失稳的判断准则，对国内多座高拱坝进行了整体抗震安全性研究。李德玉等[11]综合考虑坝与地基残余位移、坝缝开合以及坝基面开裂范围等特征，研究了白鹤滩拱坝极限抗震能力。熊堃等[12]以拱坝-地基系统代表性位移、变形量变化曲线的拐点作为评判指标，分析了乌东德拱坝的极限抗震能力。张景奎等[13]综合考虑了拱坝位移突变及坝肩滑块抗滑稳定安全因子时程，分析了拱坝-坝肩整体抗震安全。程恒等[14]以坝体关键点的位移时程曲线突变及坝基面贯通性破坏区为失稳判据，研究了沙牌拱坝整体抗震稳定性。张冲等[15]综合坝肩滑裂体动态安全系数时程、坝体应力等多种指标对拱坝-坝肩整体系统的动力稳定进行了分析。范书立等[16-17]基于拱冠位移、横缝开度和损伤体积比对白鹤滩拱坝进行了地震易损性分析。梁辉等[18]采用右岸滑块底滑动面的残余滑动位移作为指标，定义了拱坝-地基体系地震整体抗滑稳定性能水平。涂劲等[19]提出了改进的混凝土动态损伤模拟中拉压转换本构关系数值模型，并对大坝进行了地震下的损伤分析。Zhang等[20]提出了拱坝抗震安全评价的3个性能指标，包括坝踵开裂未穿透帷幕灌浆、坝体上部开裂未贯穿横截面、横缝开度未超过允许值。Alembagheri等[21]提出了基于最大坝顶位移和损伤能量耗散的损伤指标，并研究了坝体损伤状态。Amirpour等[22]以上下游面超应力面积和坝顶位移为评价指标建立IDA曲线，量化混凝土拱坝的极限状态。Yao等[23]使用坝顶变形性能指标，进行了拱坝抗震安全评价。李静等[24]提出了损伤面积比和损伤体积比来评价拱坝的地震安全性。Pan等[25]选择最大横缝开度、坝基界面开裂深度和坝体上部开裂程度作为破坏指标绘制IDA曲线，确定坝体性能水平。Hariri-Ardebili等[26]提出了基于位移、裂缝或能量的高拱坝损伤指标，并应用于混凝土高拱坝的地震损伤分析。Wang等[27]根据高拱坝动力计算的损伤分布和横缝开度提出了三种极限状态，研究了大岗山拱坝的地震易损性。Liang等[28-29]以坝肩滑块底面滑移量和滑移面积比为指标，研究了参数不确定性对高拱坝抗震稳定性的影响，并定义了基于滑动的损伤等级用于混凝土拱坝的地震稳定性影响。

可以看出，当前对高拱坝-地基系统安全评价的研究已经取得了一定进展，对抗震安全指标随着地震动强度的变化以及时程响应过程有许多探讨。目前常用的安全评价指标主要集中为坝体损伤值、坝体控制点位移、坝肩滑块位移或抗滑安全系数、坝基面开裂深度以及横缝的开度等，这些指标或单独使用或联合使用来评判高拱坝-地基系统的稳定性。坝体中上部的损伤情况影响到拱坝的挡水功能，但目前高拱坝的安全评价侧重于研究坝肩滑块稳定性和坝基面损伤对坝体安全的影响，反映坝体中上部损伤状态的评价指标较少。当下使用较多的坝顶顺河向位移以及坝体中部横缝张开度都不能很好地描述坝体中上部的损伤状态[30]，也无法反映坝块损伤后的局部稳定性，因此需要对坝体中上部的安全评价问题提出合适的评价指标，并建立局部安全评价指标与损伤、地震动强度的关系。

杨会臣等[31]在关于混凝土重力坝极限抗震能力的研究中，计算了混凝土开裂后不同形状脱离体在地震作用下的失稳过程，随着地震动放大倍数的增加，脱离体滑动位移增加最终落入下游。结合高拱坝的数值及振动台试验结果，可以看出高拱坝中上部受损破坏产生贯穿的裂缝后，混凝土块体与重力坝脱离体具有相似的失稳过程，因此层间抗滑安全系数及其持时可作为安全评价指标，探讨拱冠梁中上部的破坏规律与潜在危险层面。

本文以白鹤滩拱坝为例，建立了高拱坝-地基有限元模型，采用地震动峰值加速度(peak ground acceleration，PGA)作为地震动强度参数，将10条人工合成地震波分别调幅为12个PGA强度等级输入有限元模型进行有限元计算。结合振动台试验与数值仿真试验的结果，针对坝体中上部可能产生严重破坏的情况，以拱冠梁中上部为研究对象，考虑混凝土损伤引起的材料参数变化，逐层计算了拱冠梁中上部的层间抗滑安全系数及层间抗滑安全系数持时作为局部安全评价指标。绘制了两种指标随PGA强度变化的发展曲线，以及在不同PGA下沿高程的分布图，研究了其随PGA变化的发展规律。并分别统计了层间抗滑安全系数最小值和层间抗滑安全系数持时最大值所在的坝高位置，根据统计结果确定了拱冠梁中上部的潜在抗震薄弱面位置。本文计算结果与高拱坝振动台地震破坏试验结果相近，说明将该评价指标用于拱冠梁中上部抗震安全评价的效果良好，可为高拱坝抗震薄弱部位的定位以及大坝安全监测提供参考。

2 计算模型和计算条件

本文以289 m高的白鹤滩拱坝为例，建立了拱坝有限元模型，并进行了动力分析。图2(a)为大坝-地基有限元模型。结合实际情况，对30条坝体横缝进行了模拟，如图2(b)所示。其中X方向为横河向方向，Y方向为顺河向方向，Z方向为竖直方向。

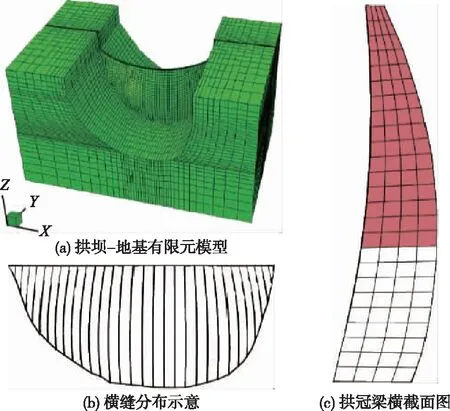
图2 坝体有限元模型

模型的材料参数主要来源于白鹤滩拱坝的设计资料，坝体混凝土和坝基参数见表1，其中混凝土强度与弹性模量均为静态取值。

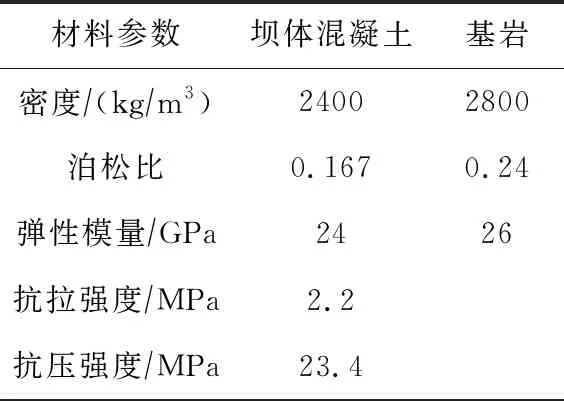
表1 材料参数

对正常水位下的拱坝模型进行了地震动力分析。坝体-库水作用采用Westergaard附加质量法[32]施加到大坝上游表面的节点上，采用杜修力等[33]提出的黏弹性人工边界来模拟无限地基的辐射阻尼，坝体部分采用混凝土塑性损伤本构。考虑到地震波的随机性，根据地震动危险性分析确定贡献最大的潜源地震区，采用有限断层法得到设定场地谱，并人工合成10条三向地震波，其反应谱如图3所示，三向地震记录如图4所示。将每条地震波均以0.1g的强度间隔调整到12个PGA强度，从0.1g到1.2g，即总共有120条三向地震波被输入模型进行模型的动力响应分析。

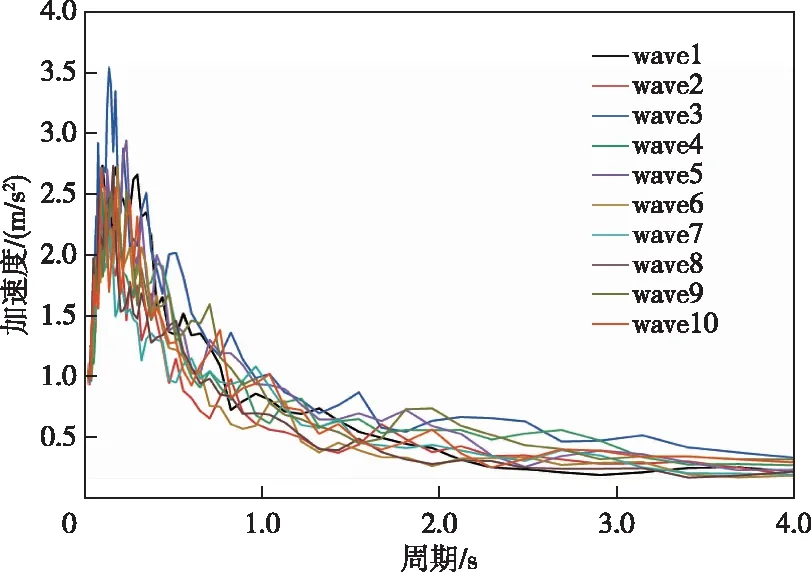
图3 人工合成地震波反应谱

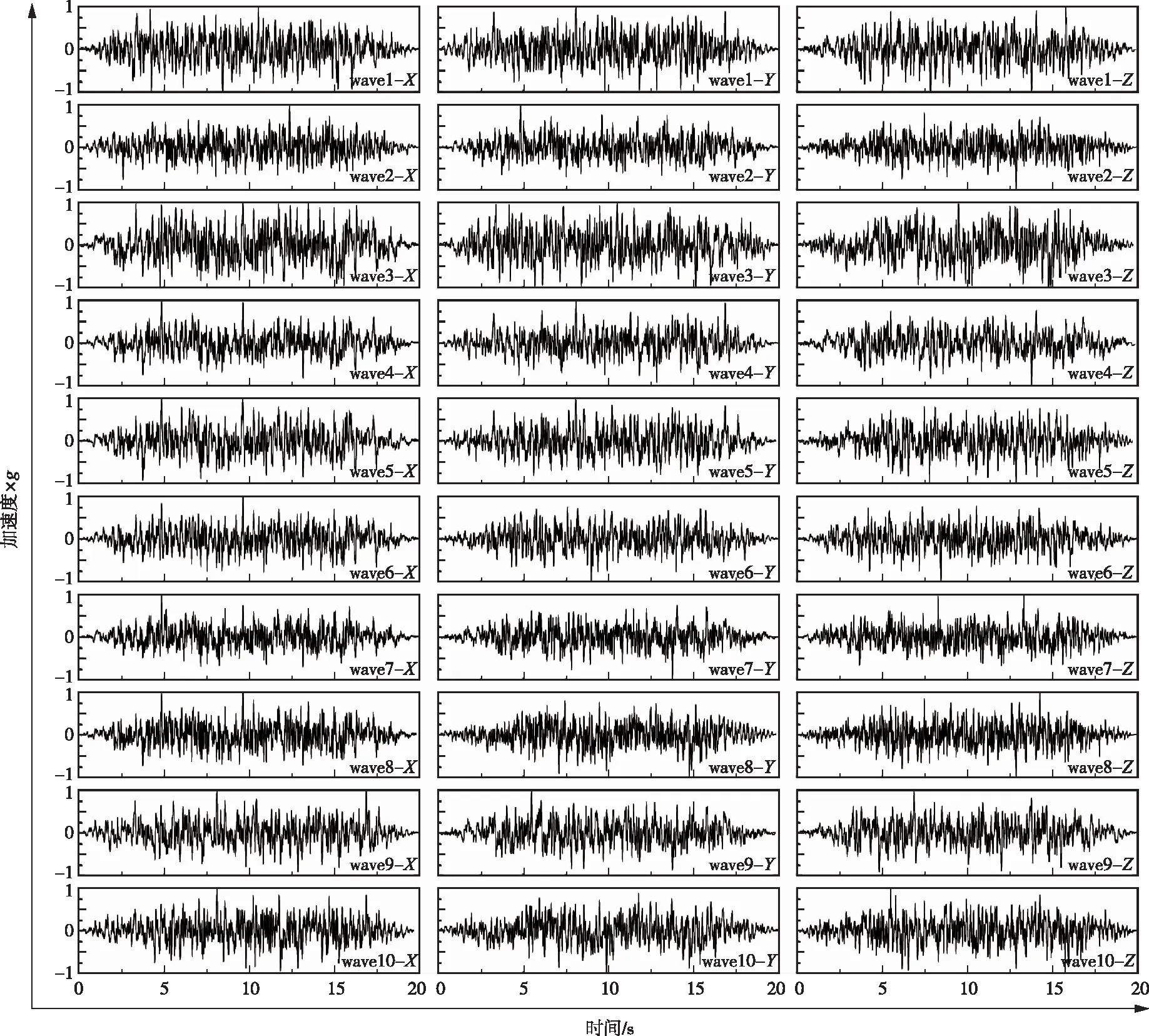
图4 归一化的人工合成地震波时程曲线

3 基于抗滑安全系数的坝段中上部抗震安全评价

在当前的高拱坝抗震安全评价中，用于反映坝体中上部损伤状态的评价指标较少，而常见的坝顶位移、坝体中部横缝开度等指标随地震动强度的发展规律难以体现坝体中上部的损伤变化情况。根据范书立等[7]学者进行的振动台地震破坏试验研究，当输入的PGA达到一定强度时，坝体混凝土将在顶拱的中部出现裂纹。进一步提高PGA，将会导致裂缝贯穿上下游，顶拱中部大约4/5高程以上的混凝土坝块在强震作用下将脱离坝体，使大坝丧失挡水功能。为了探究坝体中上部损伤随地震动强度的发展规律，本节以拱冠梁中上部(从坝顶至1/3坝高，如图2(c)所示)为研究重点，分析、探讨了层间抗滑安全系数、层间抗滑安全系数持时随PGA变化的发展规律，统计了拱冠梁中上部在强震作用下的薄弱位置。

在本节中，所有抗滑安全系数、抗滑安全系数持时及相应的统计均为拱冠梁中上部的结果，为简洁描述，在以下内容均简称为抗滑安全系数、抗滑安全系数持时。

3.1 抗滑安全系数计算公式层间抗滑安全系数按式(1)进行计算：

K=[∑(Nf+cA)]/(∑T)

(1)

式中：K为抗滑安全系数；N为垂直于滑动面的力；f为剪切摩擦系数；c为剪切黏聚力参数；A为滑动面面积；T为沿滑动面的力。

拱冠梁在地震作用下的受力如图5所示，图中，h为上游正常蓄水位到拱冠梁底部的高度；G为拱冠梁整体所受重力；FY、FZ分别为拱冠梁在顺河向和竖直向的地震动惯性力。

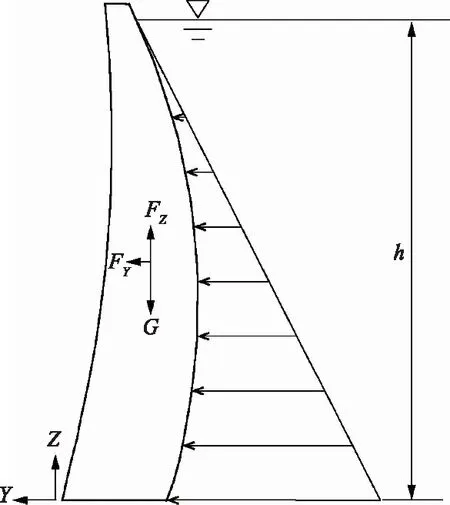
图5 拱冠梁受力示意

有限元计算中，在进行层面的抗滑稳定分析时，可以直接采用有限元分析中该层面的法向力和切向力。在本计算中，N为计算层面上各单元的法向力，T为计算层面上各单元的切向力，如下式所示。

N=NE

(2)

T=TE

(3)

式中NE、TE分别为单元法向力和单元切向力。

3.2 混凝土材料的剪切参数要计算坝段的层间抗滑安全系数，需要先获得混凝土材料的抗剪强度参数，即黏聚力参数c与内摩擦角φ。强震后，考虑到混凝土的损伤会造成混凝土强度的降低，导致黏聚力和内摩擦角的减小，使混凝土的抗滑性能受到影响。因此，确定混凝土强度折减后的黏聚力和内摩擦角的数值是关键性问题。

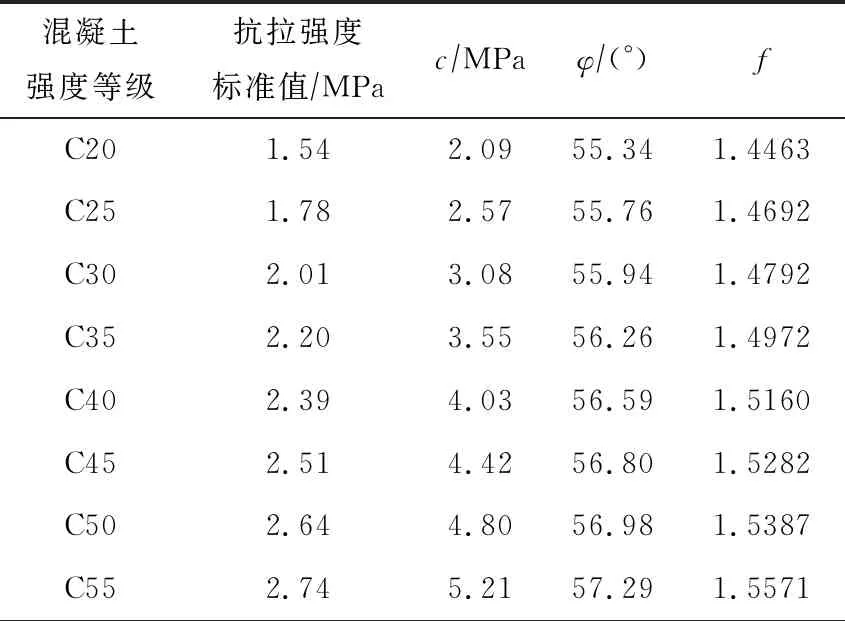
表2 不同强度等级混凝土的抗剪强度参数标准值[34]

目前，尚无混凝土抗剪强度参数c和φ的相关规范和标准，无法直接获得混凝土强度折减情况下的抗剪强度参数。因此，本文根据国内学者所进行的混凝土材料抗剪强度试验，对混凝土抗拉强度与抗剪强度参数之间的关系进行了拟合。丛宇等[34]在2015年进行了混凝土材料抗剪强度试验研究，基于岩土抗剪强度试验原理，对不同强度等级的混凝土进行了抗剪强度试验，得到了对应于混凝土强度的抗剪强度参数c和φ。表2为丛宇等[34]给出的不同强度等级混凝土的抗剪强度参数标准值，其中f是φ的正切值，也就是摩擦系数。

在本文的研究中，由于混凝土的受压损伤很小，因此认为混凝土的抗压强度保持不变，仅考虑混凝土的受拉损伤。由于指数函数对表2数据的拟合效果良好，本文根据丛宇等[34]的研究结果，采用指数函数对混凝土抗拉强度与c、f的关系进行拟合，拟合曲线如图6所示。

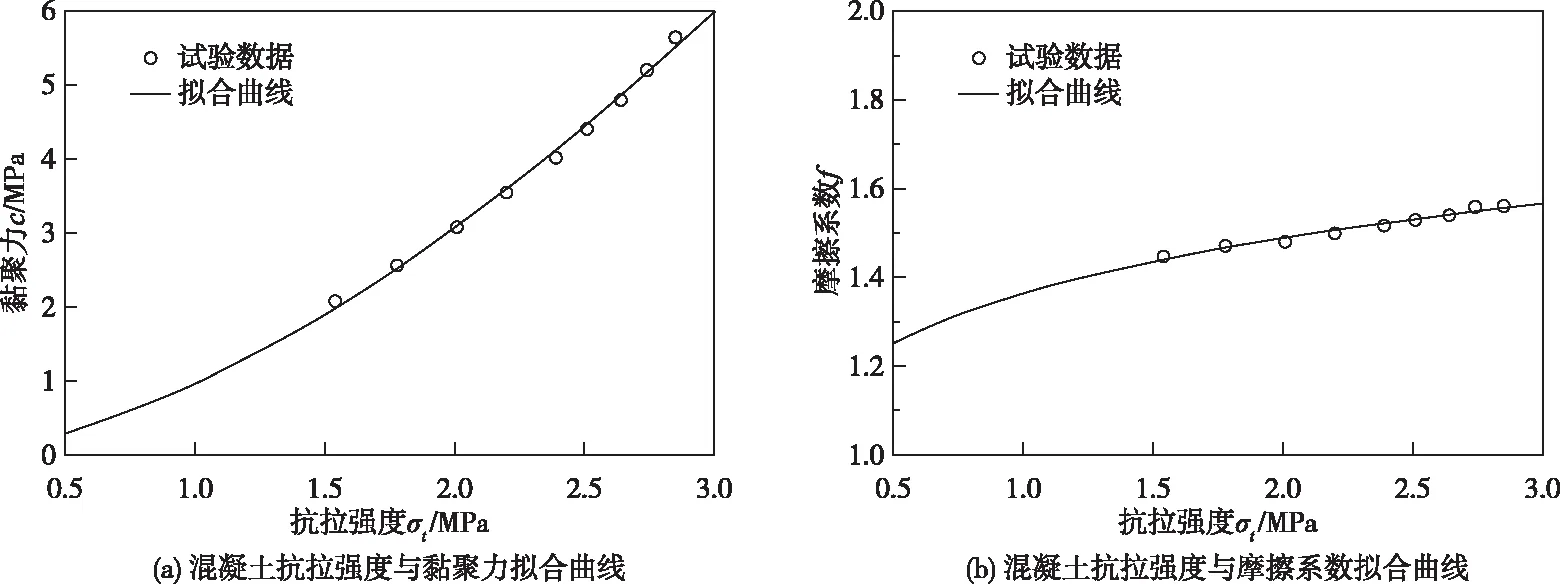
图6 混凝土抗拉强度与抗剪强度参数的拟合曲线

拟合曲线的公式如下：

c=0.9701×σt1.661

(4)

f=1.363×σt0.1258

(5)

式中：c为黏聚力参数；f为剪切摩擦系数；σt为混凝土的抗拉强度。

以上两式所对应的相关系数R2分别为0.996和0.972，说明指数函数拟合的公式符合散点的分布规律。

图7是基于规范计算的塑性损伤本构下混凝土损伤与抗拉强度的关系曲线。结合式(4)(5)，即可根据每一时刻受损混凝土的抗拉强度计算对应的抗剪强度参数c和f，进而使用3.1节中的公式计算地震动过程中每个时刻的抗滑安全系数。

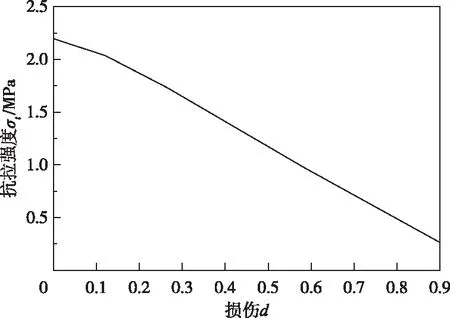
图7 损伤与混凝土抗拉强度的关系曲线

3.3 抗滑安全系数最小值分布将拱冠梁中上部在10条地震波、12个强度下坝段内的最小抗滑安全系数绘制如图8，其中横坐标轴代表的是PGA的值，纵坐标轴代表抗滑安全系数。从图中可以看出，随着PGA的逐渐增大，抗滑安全系数的最小值可以分为两个阶段。可以看出，虽然在不同的地震波下，曲线确切的转折点位置不尽相同，但总体的发展趋势是相似的。

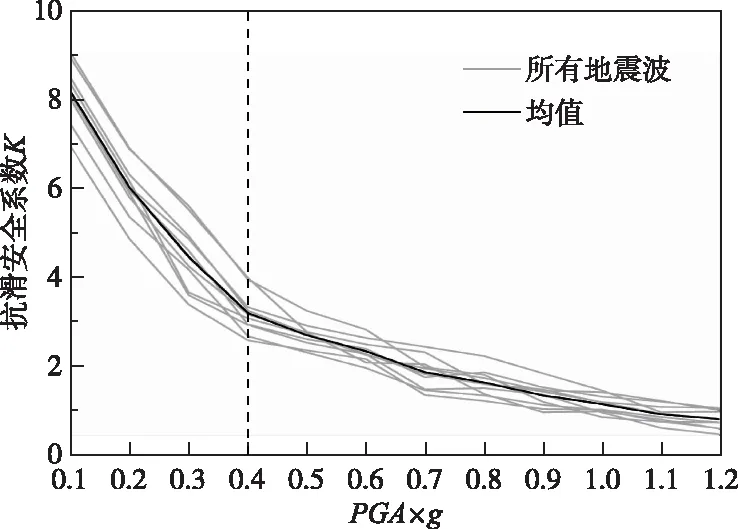
图8 抗滑安全系数最小值与PGA的变化曲线

将10条曲线的均值曲线绘制在同一张图内时，发展阶段变得更为明显。在0.4g处，曲线显示出明显的转折点。这表明在0.4g时，拱冠梁开始出现损伤，拱冠梁开始进入非线性状态。因此，抗滑安全系数的最小值可以作为评价坝段损伤状态的局部安全评价指标，其拐点出现在0.4g，可将该PGA下的抗滑安全系数最小值作为一个关键值引入后续的分析。本算例中，0.4g下的最小抗滑安全系数平均值约为3.2。

为了更明晰地表示拱冠梁坝段的抗滑安全系数分布，将拱冠梁中上部所有层面在120条地震波下的抗滑安全系数逐层进行计算，并将抗滑安全系数最小值沿高程的分布曲线绘制出，如图9所示。其中横轴代表安全系数的值，纵轴代表坝高。图中绘出了每个PGA下10条波的均值曲线以及1个正负标准差的范围曲线，并在均值曲线上将抗滑安全系数最小值的位置标出，明确平均抗滑安全系数最小值的所在。

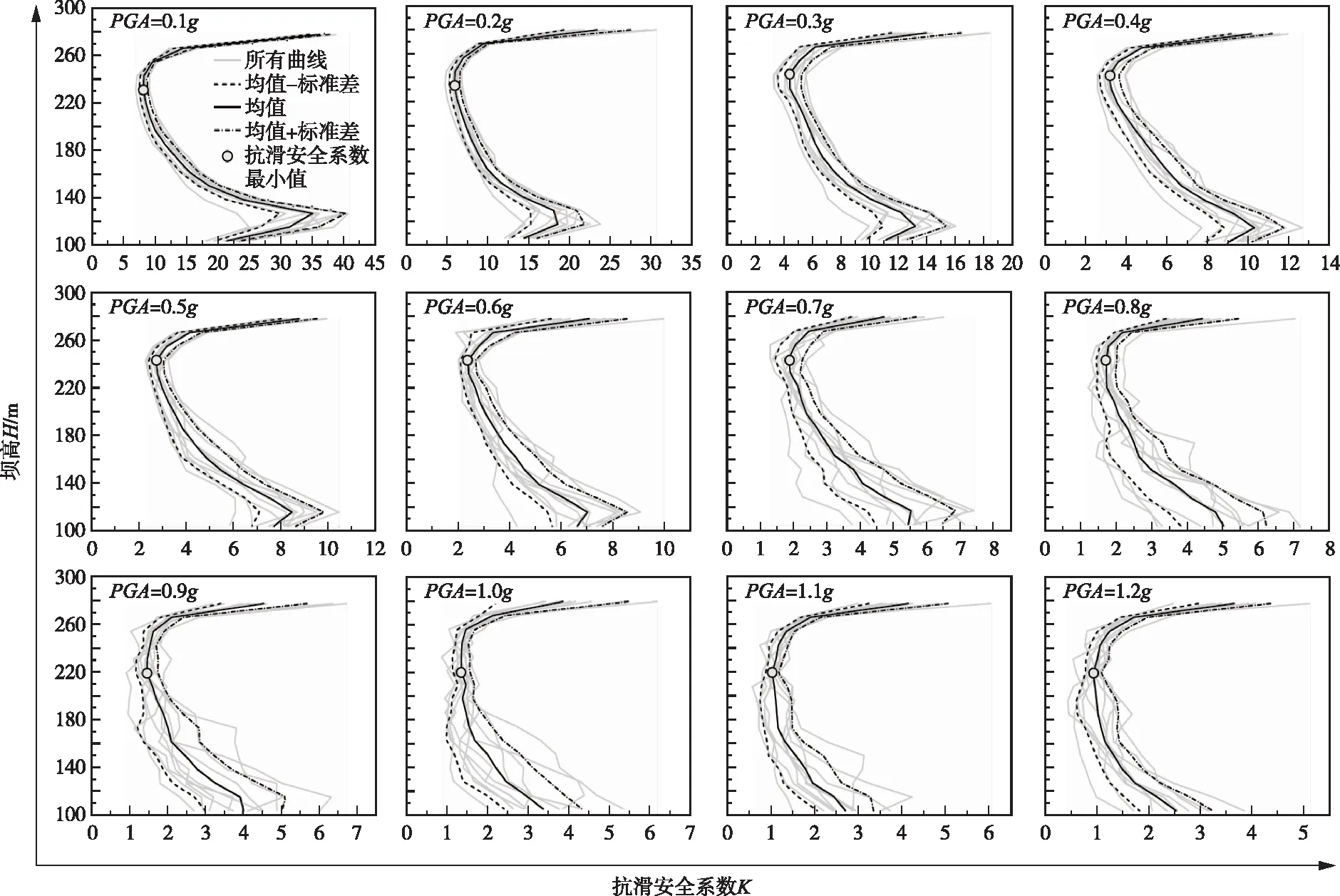
图9 抗滑安全系数最小值沿坝高的分布曲线

通过图9，可以看出抗滑安全系数最小值沿坝高的分布大致有如下规律：(1)随着高度的降低，抗滑安全系数迅速降低，然后再次升高，危险部位位于坝段的中上部分。(2)随着PGA的增加，坝段所有高程下的抗滑安全系数整体下降。(3)薄弱位置的高程随着PGA的变大发生变化，当PGA较小时，薄弱面的范围接近坝顶且范围较集中，如PGA=0.4g时抗滑安全系数最小值出现的位置在坝高240 m附近；当PGA逐渐增大时，抗滑安全系数最小值出现的位置高程降低且风险层面的范围更广，如PGA=1.2g时，在160～260 m坝高范围内的抗滑安全系数都相对较小，发生破坏的可能性很大。

总体来说，根据抗滑安全系数随PGA的变化图，可获取拱冠梁抗滑安全系数在PGA不断增加情况下的变化趋势。抗滑安全系数沿坝高的分布图可以描述拱冠梁在地震下发生破坏的危险区域的变化情况，当PGA较大时，拱冠梁中上部分可能会发生破坏，且危险区域的位置逐渐向坝踵移动并扩大。

3.4 抗滑安全系数最小值出现位置统计上节中描述了随着PGA的增加拱冠梁内抗滑安全系数最小值的发展趋势，以及在坝段内沿坝高的分布规律。本节对各个地震动强度下拱冠梁中上部位抗滑安全系数最小值出现的坝高进行统计，以找出最危险的薄弱面所在位置。

如图10所示，将每个PGA强度下拱冠梁中上部抗滑安全系数最小值所在坝高进行统计，可以更直观地看出薄弱面所集中的位置(阴影标注部分)。图中横轴为地震波编号，纵轴为抗滑安全系数最小值所在位置的坝高。

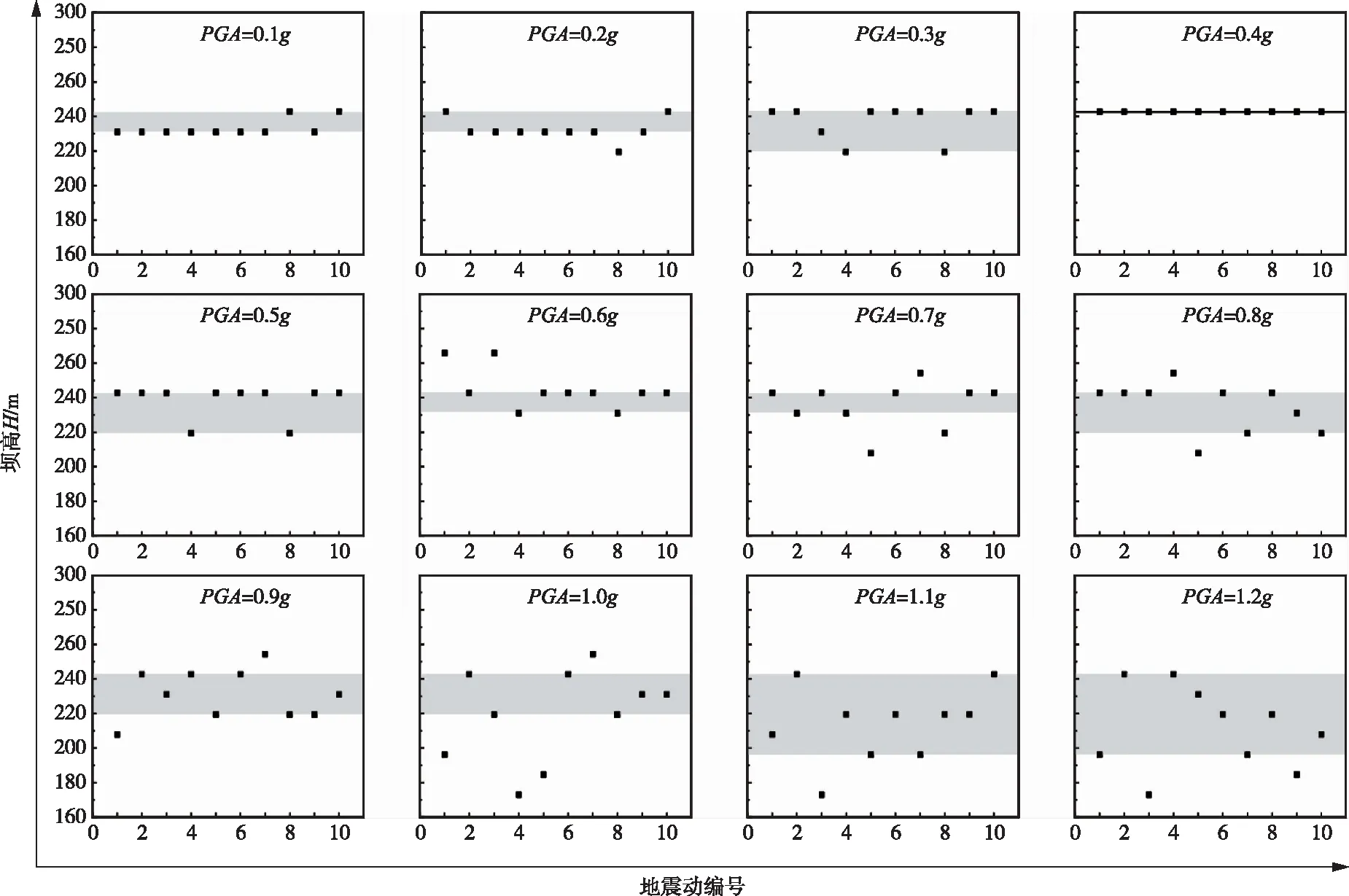
图10 拱冠梁中上部抗滑安全系数最小值所在坝高

从图10中，可以得到与图9相似的规律。当PGA较小时，抗滑安全系数最小值集中出现在220～240 m坝高位置。当PGA达到0.7g时，抗滑安全系数最小值所在的高程范围开始出现了扩大，当PGA达到1.2g时，抗滑安全系数最小值出现位置的范围扩大到170～240 m坝高。这表明随着PGA的升高，最危险层面的位置整体是从坝段上部向坝段中部位置发展的。

用H表示坝高，则在本研究中，PGA≤1.0g时，抗滑安全系数最小值出现的集中位置为220～240 m坝高，约为0.76～0.83H。PGA为1.1g至1.2g时，抗滑安全系数最小值出现的主要范围为200～240 m坝高，约为0.69～0.83H。与范书立等[7]所进行的振动台试验结果较为一致，符合实际情况。

综上所述，坝段的层间抗滑安全系数可以在一定程度上反映坝体局部的损伤发展趋势，数值分析结果与已有的振动台试验结果一致，符合实际。因此可以考虑将坝段层间抗滑安全系数作为描述拱坝局部损伤情况的评价指标。

3.5 拱冠梁抗滑安全系数持时根据抗滑安全系数最小值出现位置的统计结果，可以发现虽然安全系数最小值出现的位置具有一定的规律，但当PGA升高时，其出现位置的分散度也较高。并且在整个震动时程中，可能出现在某一时刻抗滑安全系数达到最小值，在下一时刻又恢复正常值的情况。因为拱坝为高次超静定结构，具有应力重分布的特点，有着极强的自身调节能力，因此瞬时的较小抗滑安全系数并不能说明拱坝局部发生破坏。

显然，层间抗滑安全系数具有随时程来回震荡的特性，这使得单独用整个震动时程中的抗滑安全系数最小值来评价拱坝中上部的安全性是不够准确的。因此，本节计算不同层面中抗滑安全系数在整个震动时程中小于某个关键值的持续时间，来更准确地判断坝段内最易发生破坏的位置。根据3.3节的计算结果，在本研究中将此关键值设置为0.4g时的抗滑安全系数最小值的平均值3.2。

计算拱冠梁每个层面的抗滑安全系数小于等于3.2的持时，并将每个强度下的坝段内持时最大值绘制在一张图中，可以得到持时最大值随PGA的变化曲线，如图11所示。图中横轴为PGA的值，纵轴为坝段内抗滑安全系数小于等于3.2在整个震动过程中的持续时间最大值，以下简写为TK≤3.2，K为抗滑安全系数。

从图11可以看出，各条地震波下，拱冠梁中上部的TK≤3.2具有较为相似的发展曲线，在0.4g至0.5g开始出现抗滑安全系数小于等于3.2的情况，当PGA增加时，TK≤3.2的增长速度也开始增加。在PGA达到一定水平后，TK≤3.2增长速度进一步加大。

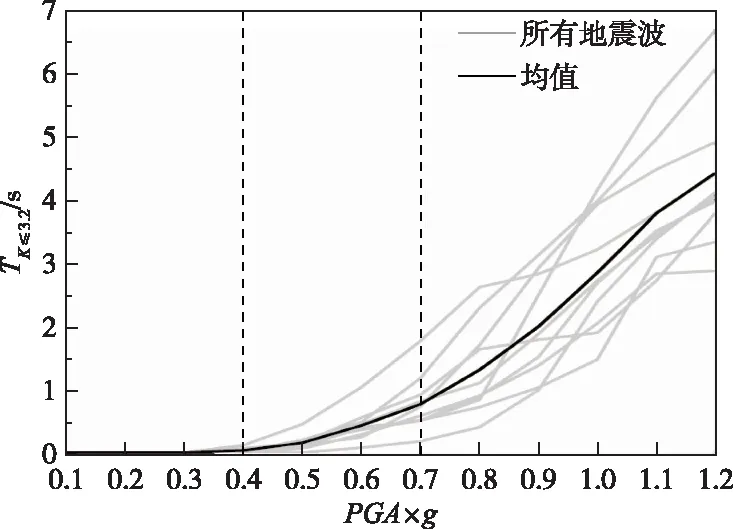
图11 抗滑安全系数持时最大值与PGA的变化曲线

将均值曲线绘出，可以大致分为三个阶段。PGA在0.1g～0.4g时，平均TK≤3.2增长缓慢，其值非常小，不超过0.1 s。当PGA增加至0.4g后，平均TK≤3.2的增长速度提高，PGA每提高0.1g，平均TK≤3.2增幅在0.1～0.35 s之间。当PGA提高至0.7g时，平均TK≤3.2的增长速度进一步提升，PGA提高0.1g，平均TK≤3.2增幅均大于0.5 s。

将10条波情况下的各层面抗滑安全系数持时的均值沿高程的分布图绘制出，如图12所示。其中横轴为抗滑安全系数小于等于3.2的持续时间，纵坐标代表坝高。由于PGA小于0.4g情况下的TK≤3.2很小，因此不将其纳入分析范围。

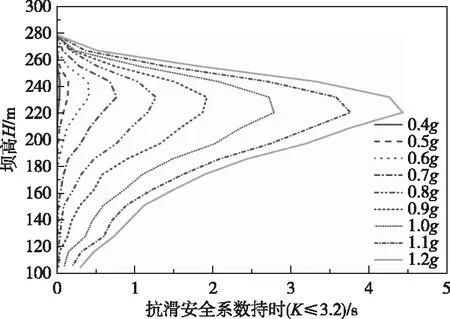
图12 抗滑安全系数持时最大值沿坝高的均值分布曲线

从图12中可以看出，抗滑安全系数持时沿坝高的分布有以下特点。(1)沿坝高减小的方向，抗滑安全系数持时呈现先升高再降低的特点，且在关注坝段高度的两端都接近于0，说明破坏主要出现在拱冠梁上部位置。(2)随着PGA的增加，拱冠梁中上部抗滑安全系数持时整体呈现增大趋势，其中220 m坝高附近的抗滑安全系数持时增长最明显。(3)随着PGA的增加，抗滑安全系数持时最大值所在的位置从240 m坝高附近降低到220 m坝高附近，但潜在危险层面所在的坝高范围没有显著增大。

3.6 抗滑安全系数持时最大值出现位置在3.5小节中，研究了抗滑安全系数持时最大值的发展趋势以及沿高程的分布规律，但不能明确抗滑安全系数持时最大值所在的具体位置。本节统计了各PGA下抗滑安全系数持时最大值出现的高程，用以确定最薄弱面的所在位置。由于在0.1g～0.3g下安全系数小于等于3.2的情况很少，基本处于稳定状态，因此本节的统计结果从0.4g开始。最终统计图如图13所示，抗滑安全系数最大值出现的集中范围用阴影部分标出。

与图10相比，抗滑安全系数持时最大值出现的位置要更加集中，规律性也更明显。随着PGA逐步增大，抗滑安全系数持时最大值出现的坝高范围从230～240 m坝高下移到220～230 m坝高，虽然下降的高度较小，但也能说明危险层面所在位置是逐渐降低的，这与抗滑安全系数最小值所在位置表现出的规律基本一致。

从图13中可以看出，当PGA为1.2g时，抗滑安全系数持时最大值所在的集中位置大致为220～230 m坝高。如果用H表示坝高，则抗滑安全系数持时最大值的所在位置为0.76～0.79H。该坝高范围比使用抗滑安全系数最小值统计的坝高范围更为精准，同时也符合范书立等[7]进行的振动台试验中坝体混凝土折断掉落的高度，是高拱坝抗震安全的薄弱部位，在实践中应予以着重设防。

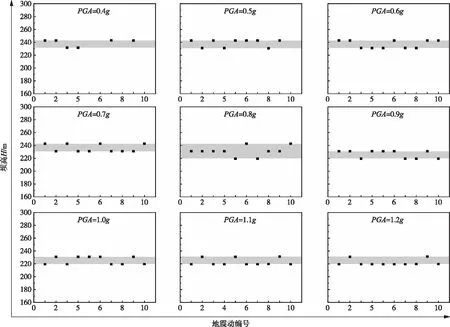
图13 拱冠梁中上部抗滑安全系数持时最大值所在坝高

4 结论

根据以往的研究成果，高拱坝中上部在地震作用下损伤发展迅速、易发生破坏，因此有必要研究高拱坝中上部的地震损伤发展规律。本文引入层间抗滑安全系数及层间抗滑安全系数持时作为局部抗震安全评价指标，以白鹤滩双曲拱坝作为算例，采用地震动超载法对有限元模型进行动力分析，并对拱冠梁中上部的地震破坏规律进行了探讨，得到以下结论。(1)本文将层间抗滑安全系数和层间抗滑安全系数持时引入高拱坝局部抗震安全研究中，利用这两个指标对拱冠梁中上部的损伤发展规律和抗震薄弱位置进行了探讨，研究结果表明，地震动强度增加时拱冠梁中上部的安全性明显降低。(2)通过对抗滑安全系数持时最大值所在位置进行统计，可以发现利用持时得到的危险位置范围比采用抗滑安全系数得到的范围更加集中，规律性也更明显。这是由于拱坝作为高次超静定复杂结构，具有较好的自调节能力。因此通常情况下，仅使用瞬时的层间抗滑安全系数最小值来确定拱冠梁危险位置的方法是不够精准的，需要联合其他指标进行综合评判。(3)综合考虑抗滑安全系数最小值与抗滑安全系数持时最大值所在位置的统计结果。随着地震动强度的增加，拱冠梁中上部的抗震薄弱位置是逐渐降低的。本文的统计结果与其他学者进行的高拱坝振动台试验结果较为一致，表明所提出的指标应用于高拱坝的效果较好，可为未来高拱坝局部抗震安全评价指标的研究以及地震安全监测的布置提供一些可行的思路。

需要注意的是，本文计算结果均基于白鹤滩拱坝的动力响应分析。由于所处的地形、地质条件不同，拱坝的体型可能存在较大差异，不同拱坝的响应规律也不尽相同。作为高拱坝中上部局部抗震安全评价指标的初步探讨，本文提出的评价指标尚需进一步完善。未来，在探讨类似体型的高拱坝中上部是否有相似的损伤发展规律，建立高拱坝抗震安全评价指标体系，以及在建立拱坝中上部局部抗震安全评价指标与坝体损伤值、可监测响应之间的相关关系方面，还可以进一步深入研究。