融合改进符号动态熵和随机配置网络的水电机组轴系故障诊断方法

陈 飞，王 斌，周东东，赵志高，丁 晨，陈帝伊

(1.西北农林科技大学 水利与建筑工程学院，陕西 杨凌 712100；2.武汉大学 水资源与水电工程科学国家重点实验室，湖北 武汉 430072)

1 研究背景

随着水电机组朝着巨型化和智能化方向发展，复杂的机械结构以及多变的运行任务导致机组发生故障的概率进一步增大。作为低速旋转机械的代表，水电机组故障是一个渐变的过程，通过监测系统获取机组振动状态数据，结合故障诊断技术实现机组故障的提前预警是水电机组故障诊断的主要途径[1-2]。轴系作为水电机组的关键部件，其振动是影响电站运行安全稳定的重要因素，水电机组事故大多由轴系故障引发。因此，针对水电机组轴系开展故障诊断研究对维护机组安全稳定运行具有重要的工程价值。

伴随监测系统的日趋完善，水电机组振动信号呈现出高维和多源的特点[3]，如何整合多个传感器振动信号提取更为可靠的特征成为水电机组轴系故障诊断的关键。现有水电机组轴系故障诊断研究主要建立在单一振动信号数据基础上，通过特征提取和模式识别等步骤完成机组故障诊断工作[4-6]。尽管这些工作有时可以取得不错的诊断效果，但无法全面刻画机组故障特性，加之每种故障发生的部位各异造成传感器测点难以选择等问题，都导致基于单一振动信号进行水电机组轴系故障诊断具有巨大的不确定性。因此，融合多元振动信号进行故障诊断可以有效提高获取机组故障特征的客观性和可靠性。然而，不同部位传感器振动信号具有一定的耦合性，如何在考虑多元振动信号相关性的前提下提取水电机组轴系故障特征是融合多元振动信号的难点。熵作为一种衡量时间序列复杂度的工具，被广泛应用于水电机组故障特征提取领域[7-9]。例如，党建等[8]提出了一种基于多维度排列熵和支持向量机相结合的水电机组故障诊断方法，实现了水电机组故障的精确识别。随着熵理论研究的不断深入，学者们基于多尺度熵和多维嵌入理论将单一信号时序评估扩展到了多元信号领域[10-11]，实现了对多元时序信号复杂度的评估。但是，传统多元多尺度熵存在抗噪能力弱以及粗粒化程度不足等问题，针对这些问题，文献[12]中提出精细复合多元多尺度符号动态熵(Refined composite multivariate multiscale symbolic dynamic entropy，RCMMSDE)的概念。凭借符号动态熵良好的抗噪性能和改进的粗粒化方式[13-14]，使得RCMMSDE提取的特征更加客观和可靠。因此，论文利用RCMMSDE作为特征提取工具，提取不同水电机组状态振动信号的特征。

将故障特征输入到分类器中进行模式识别是水电机组故障诊断的重要组成部分。近年来，以人工神经网络和深度学习为主的算法被用于水电机组模型构建[15]、轴心轨迹识别[16]以及振动趋势预测[17]等领域。文献[18-20]将支持向量机(Support vector machine，SVM)、反向神经网络(Back propagation neural network，BPNN)以及卷积神经网络(Convolutional neural network，CNN)充当分类器，结合故障特征有效区分了水电机组不同类型故障。然而，过度依赖超参数和漫长的训练时间都限制了这些模型在水电机组故障诊断方面进一步应用。作为随机参数神经网络最新模型[21]，随机配置网络(Stochastic configuration network，SCN)凭借独特的监督机制和增量的网络模型，在处理大规模高维数据上具有人为参数少、训练时间短以及收敛速度快等优点[22-23]，在化学医药[24]、风速预测[25]以及航空工业[26]等方面都有着广泛的应用。本文将RCMMSDE提取的特征输入SCN网络中，完成水电机组轴系故障的模式识别工作。

鉴于RCMMSDE在多元时序信号中良好的特征提取能力，提出了一种基于RCMMSDE和SCN相结合的水电机组轴系故障诊断方法。本文利用RCMMSDE提取不同状态水电机组轴系故障特征，并将特征输入到SCN中进行故障识别。通过对比水电机组多元振动信号和单一振动信号两种不同场景下不同模型的诊断效果，验证了所提模型的有效性。

2 RCMMSDE-SCN水电机组轴系故障诊断模型

2.1 多元符号动态熵(Multivariate symbolic dynamic entropy，MvSDE)作为RCMMSDE的基础，MvSDE将符号动态熵应用范围扩展到多元时序信号领域。MvSDE模型可简单概括为以下几个部分[27]：

(1)采用最大熵划分算法(Maximum entropy partitioning，MEP)将时序序列分成ε个区间，并通过式(1)对时序序列进行符号化处理：

(1)

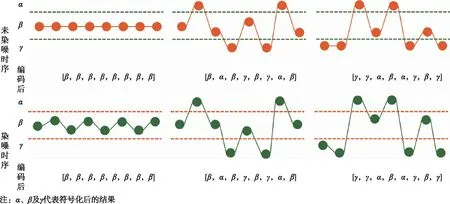
图1 MEP算法符号化处理过程

(2)通过D-Markov机描述符号序列之间的后续状态和转移概率，定义不同的状态序列，将时间序列转换成时间相关矩阵：

(2)

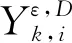
(3)

式中：type(·)为从符号序列到状态序列的映射；qa和qb为不同的状态序列。

(3)通过式(4)计算多元时序的状态转移矩阵Πm：

(4)

式中Πk，m为第k个序列转移矩阵中第m个元素。

(4)根据式(5)计算MvSDE：

(5)

2.2 精细复合多元多尺度符号动态熵(RCMMSDE)多元多尺度符号动态熵(Multivariate multiscale symbolic dynamic entropy，MMSDE)将MvSDE扩展到多个尺度下进行复杂度评估，但粗粒化不足使得MMSDE提取的特征具有较大波动性。RCMMSDE引入精细复合技术有效克服了粗粒化不足的问题，其主要内容可以概括为以下几个步骤[12]：

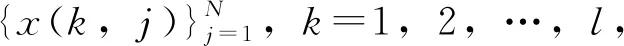
(6)

式中τ为尺度因子。

(3)根据式(7)计算多元时间序列的RCMMSDE：

(7)

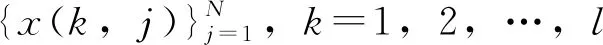
2.3 随机配置网络(SCN)通过RCMMSDE提取水电机组轴系故障特征，并将特征输入到SCN中完成故障模式识别工作。SCN作为一种具有监督机制的新型随机权重神经网络，不同于常规的前馈神经网络，SCN是根据监督机制逐步构建的，该机制约束了随机输入权重和偏差的特定取值范围。这种监督机制保证了给定非线性映射所产生SCN模型的通用逼近特性。SCN的详细过程描述如下：

(1)给定一个训练数据集{W，P}，其中W为输入数据；P为输出数据。假设SCN模型具有S-1个隐含节点，那SCN的输出ZS-1为：

(8)

式中：βi=[βi，1，βi，2，…，βi，d]T为第i个隐含节点的输出权重，d为输出维度；ωi和bi分别为第i个隐含节点的输入权重和偏置；g(·)为SCN模型的激活函数。同时，根据式(9)可计算当前网络的误差eS-1：

eS-1=[Z-ZS-1]=[eS-1，1，eS-1，2，…，eS-1，d]

(9)

(3)SCN引入监督机制为隐含节点S分配参数，具体监督机制形式如下：

(10)

(11)

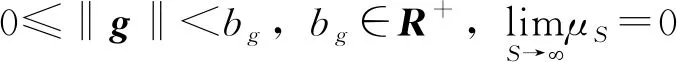
(4)利用最小二乘法计算出隐含层输出权重：

(12)

不断增加隐藏层节点，重复式(8)到式(12)，直至模型误差‖eS‖达到期望的误差容限χ或者隐函节点数达到最大隐含节点数Smax，最终输出最优模型。同时，参考文献[29]中SCN超参数设置原则，文中将输入权重和偏置的比例因子λ设置为{0.5，1，5，10，30，50，100，150，200，250}，正则化参数r设置为{0.9，0.99，0.9999，0.999 99，0.999 999}，误差容限χ设置为0.01。

3 仿真实验

3.1 RCMMSDE抗噪性能分析为验证RCMMSDE算法的抗噪性能，通过式(13)模拟不同噪声环境下水电机组“外8”形的转子轴心轨迹。如图2所示，加入噪声后，机组转子轴心轨迹进一步复杂化。

图2 不同状态不对中故障轴心轨迹图

(13)

式中：x(t)、y(t)为X和Y方向的振动位移；ω为角频率；A1、A2、B1以及B2为不同方向位移的幅度值；α1、α2、β1以及β2为不同方向位移的初始相位；z(t)为噪声信号，文中取50 dB、40 dB、30 dB、20 dB以及10 dB的高斯白噪声。

显而易见，轴心轨迹图像是由X和Y两个不同方向的振动信号组成，通过RCMMSDE、MMSDE等多元多尺度熵表征不同噪声环境下轴心轨迹的特征信息，结果如图3所示。从图中可以看出，相较于振动信号的MMSDE，RCMMSDE更为平滑，说明噪声对RCMMSDE影响较弱。同时，通过相关系数来衡量染噪前后(SNR为50 dB、40 dB、30 dB、20 dB以及10 dB)信号的差异程度，得出RCMMSDE相关系数为100%、100%、99.97%、99.26%以及95.01%，验证了RCMMSDE具有良好的抗噪性能。

图3 不同噪声下多元多尺度熵分布情况

3.2 MaFaulDa机械故障数据基于MaFaulDa机械故障数据库[30]，本文模拟水电机组常见的不对中、不平衡、内圈故障等轴系故障和零件故障。将振动信号划分为正常、水平不对中、垂直不对中、不平衡、外圈、外圈-不平衡、滚动体、滚动体-不平衡、保持架以及保持架-不平衡(下文简称“Nor”、“HM”、“VM”、“UB”、“OR”、“OR-UB”、“BA”、“BA-UB”、“CA”以及“CA-UB”)等10类不同状态振动信号。

以轴向、径向和切向(下文简称X、Y以及Z方向)三个不同方向的振动信号作为研究对象。其中，系统采样频率为50 kHz，每种状态振动信号各收集50组样本，每个样本包含5000个样本点。图4展示了不同状态的三轴振动信号，从图中可以看出不同状态振动信号中包含大量噪声，如何在噪声环境下提取有效故障信息成为水电机组轴系故障诊断的关键。

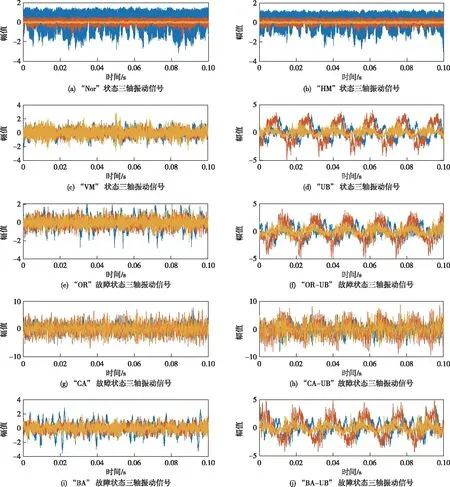
图4 不同状态三轴振动信号

3.2.1 RCMMSDE提取特征 通过RCMMSDE等多元多尺度熵提取水电机组轴系不同状态的有效故障特征。图5给出了RCMMSDE和MMSDE两类不同熵的特征提取情况，从图中可以看出RCMMSDE和MMSDE分布基本一致，总体呈现出递减的趋势。但是，单从熵值分布情况根本无法有效区分各种状态故障信号。

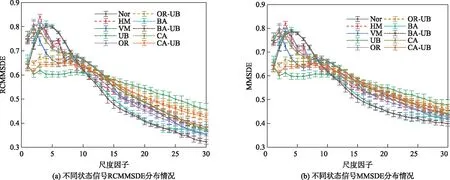
图5 不同状态信号多元多尺度熵分布情况

因此，引入T-SNE对从振动信号提取到的RCMMSDE等多元多尺度熵进行降维可视化处理。图6给出了不同状态信号的RCMMSDE、MMSDE、精细复合多元多尺度熵(Refined composite multivariate multiscale entropy，RCMMSE)以及多元多尺度熵(Multivariate multiscale entropy，MMSE)的二维特征可视化结果，从图6中可以看出RCMMSE和MMSE两种多元多尺度熵提取的故障特征混叠现象严重，其中外圈、支撑架等故障完全混杂在一起，说明RCMMSE和MMSE特征提取能力较弱。相较于RCMMSE和MMSE的杂乱无章，RCMMSDE和MMSDE基本将各类故障区分开，但在“CA-UB”和“OR-UB”、“CA”和“OR”等故障产生了小规模的混杂。此外，通过MMSDE提取的特征中“BA-UB”和“BA”故障信号发生了一定的混杂。通过对比不同熵的特征可视化结果，得出RCMMSDE具有良好的特征提取能力。

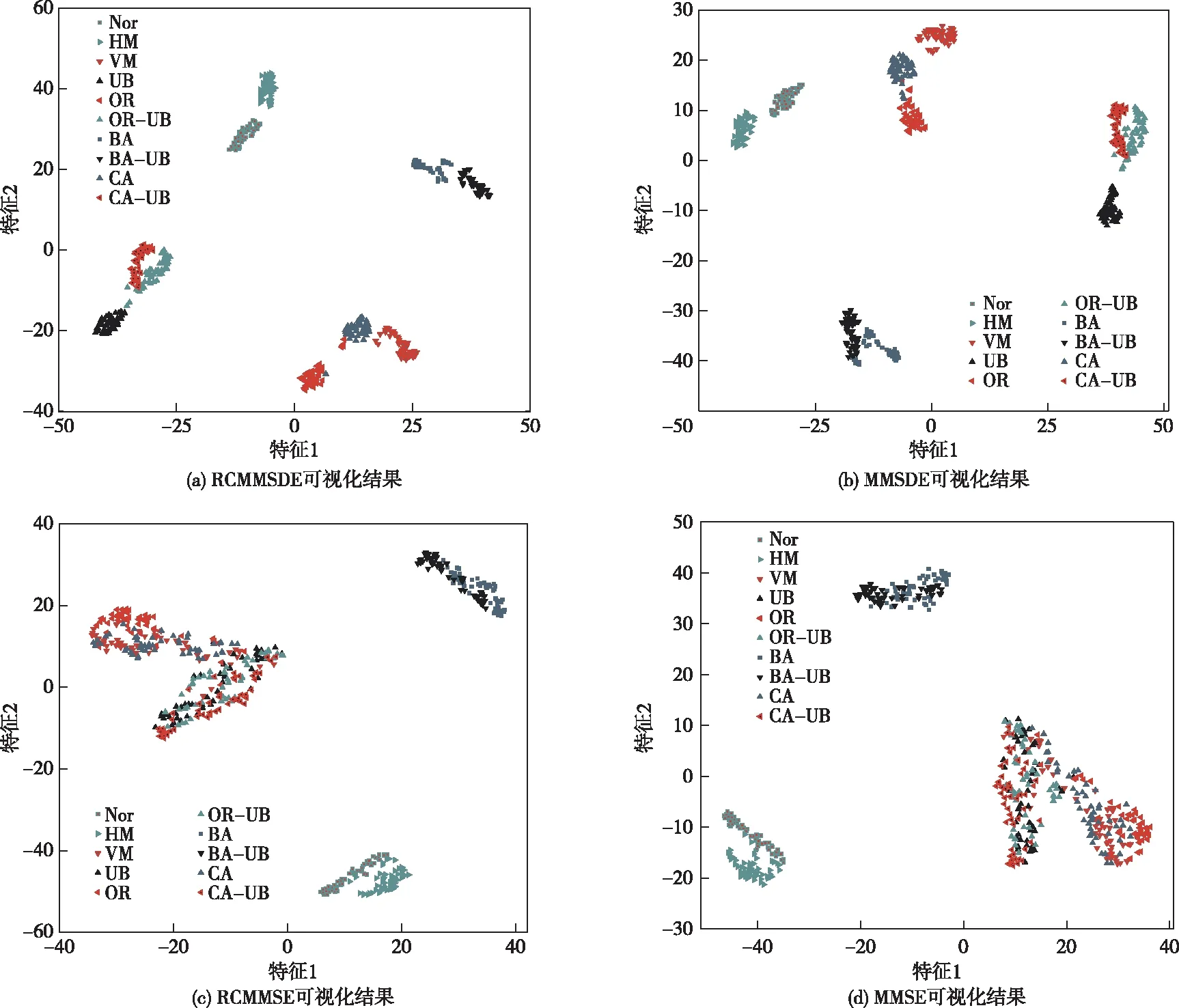
图6 不同多元多尺度熵可视化结果

3.2.2 故障识别 将RCMMSDE等多元多尺度熵提取的特征输入到SCN中进行不同故障信号的识别，考虑到Smax是影响SCN网络诊断性能的重要参数，文中分析了Smax≤100情况下RCMMSDE-SCN和MMSDE-SCN两个不同模型的诊断效果。同时，为避免随机实验对最终结果的影响，采用五折交叉验证的方式划分训练集和测试集进行测试，每个模型独立运行10次，采用诊断率的均值和标准差两个指标衡量模型的诊断效果，结果如表1所示。从表1中可以看出当Smax≤20时，由于训练不充分等问题，导致模型诊断率低下。之后随着Smax增加，两个模型的诊断进一步提升，Smax为100时两个模型分别取得了97.58%和94.78%的最佳诊断率。通过上述分析，文中将Smax设置为100。此外，两个模型在不同Smax下的诊断情况表明，RCMMSD-SCN的诊断率都远高于MMSDE-SCN，并通过标准差这个指标得出RCMMSDE-SCN诊断出的结果更为稳定。

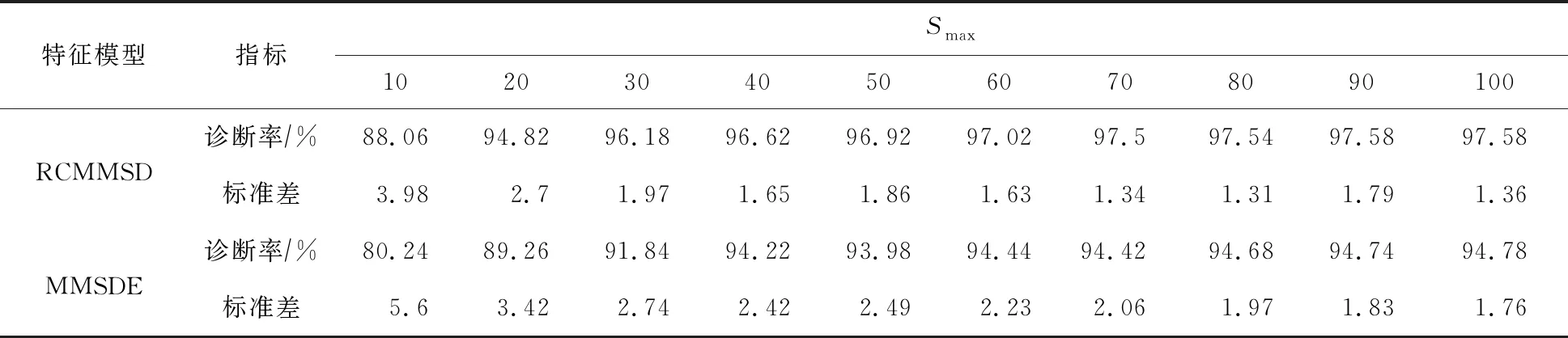
表1 不同最大隐含节点下模型的诊断情况

图7给出了RCMMSDE-SCN等模型的具体诊断结果，从图中可以看出RCMMSDE-SCN模型取得了97%的诊断率，其中有1个“CA”故障被误判为“OR”故障，1个“OR-UB”故障被误判为“UB”故障，1个“OR”故障被误判为“CA”故障，这与图4降维后结果分析基本一致。同时，MMSDE-SCN取得92%的诊断率，其无法有效区分“CA-UB”和“OR-UB”、“CA”和“OR”等故障，而RCMMSE-SCN和MMSE-SCN仅取得了82%和73%的诊断率，远低于RCMMSDE-SCN模型。

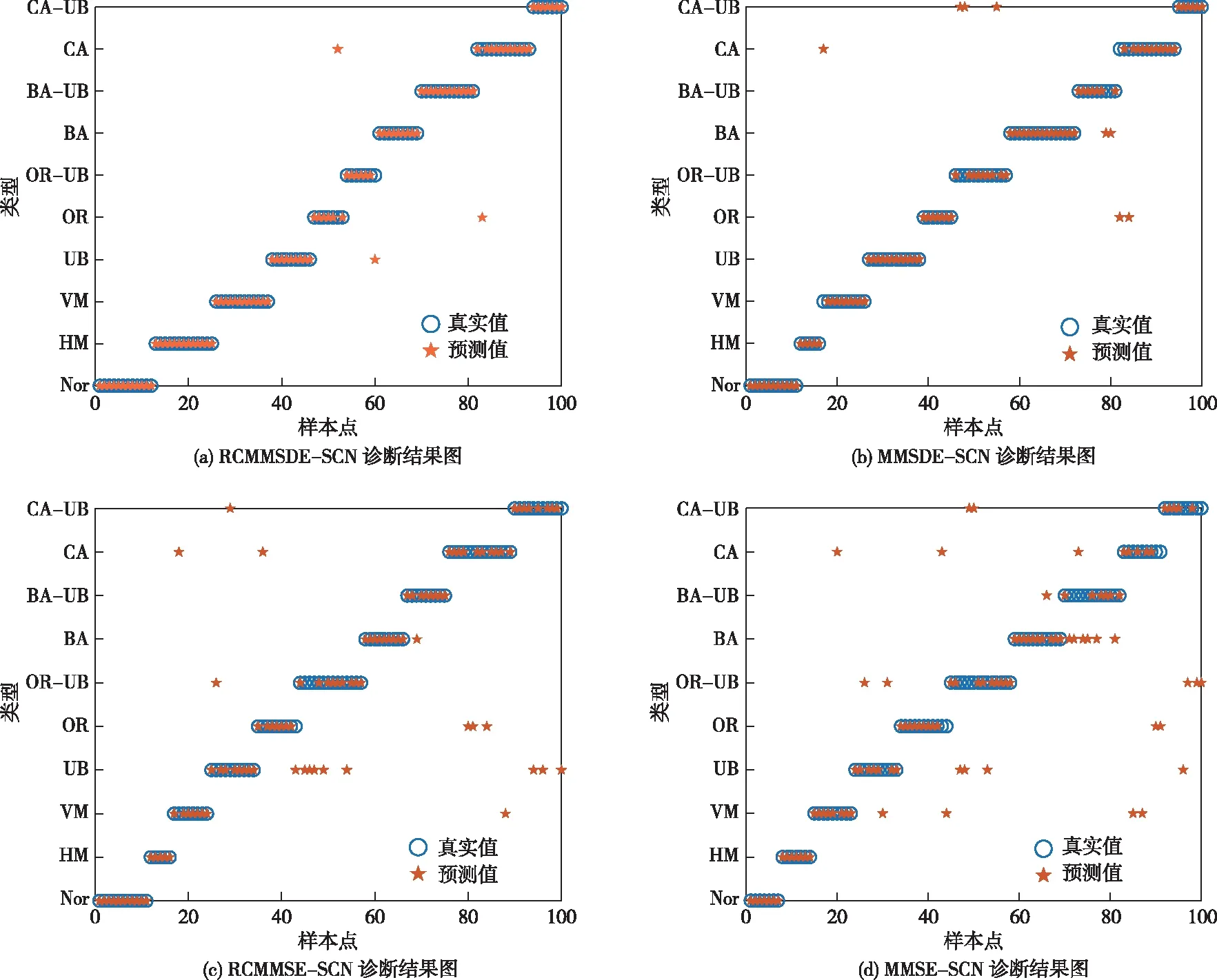
图7 不同诊断模型的识别结果图

为进一步验证所提方法的合理性和优越性，本文引入精细复合多元多尺度散布熵(Refined composite multivariate multiscale dispersion entropy，RCMMDE)[31]、多元多尺度散布熵(Multivariate multiscale dispersion entropy，MMDE)[32]、精细复合多元多尺度模糊熵(Refined composite multivariate multiscale fuzzy entropy，RCMMFE)[33]及多元多尺度模糊熵(Multivariate multiscale fuzzy entropy，MMFE)[34]等多元多尺度熵展开对比实验。通过这些多元多尺度熵提取振动信号特征，然后输入到SCN中完成识别工作。同样，采用5折交叉法划分训练集和测试集，每个模型单独运行10次，诊断情况见表2。如表2所示，RCMMSDE-SCN模型取得了97.58%的诊断率，相较于其它模型(MMSDE-SCN、RCMMDE-SCN、MMDE-SCN、RCMMSE-SCN、MMSE-SCN、RCMFE-SCN以及MMFE-SCN)提高了2.8%、6.32%、13.32%、14.2%、22.8%、3.5%以及10.48%的诊断率。同时，对比不同模型的标准差得出RCMMSDE的诊断效果最为稳定。通过上述分析，得出RCMMSDE-SCN模型是一种稳定、精确的水电机组轴系故障诊断模型。

表2 不同模型的诊断情况

如表3所示，依次分析了X、Y以及Z方向三个不同传感器振动信号下精细复合多尺度符号动态熵(Refined composite multiscale symbolic dynamic entropy，RCMSDE)和多尺度符号动态熵(Multiscale symbolic dynamic entropy，MSDE)的诊断情况，得出采用多传感器振动信号的RCMMSDE-SCN相对于单一传感器振动信号(X、Y以及Z方向)提升了14.98%、11.62%以及1.94%的诊断精度，而采用MMSDE-SCN相比单一传感器振动信号提升了20.26%、11.26%以及0.44%的诊断率，验证了融合多元传感器振动信号可以有效提升水电机组轴系故障诊断精度。

表3 不同传感器振动信号的诊断情况

3.3 HZXT-008型转子试验台故障数据为进一步验证融合多元传感器振动信号的优势，本文通过HZXT-008型转子故障试验台模拟水电机组中常见的轴系故障振动信号。如图8所示，通过控制故障件的故障程度，将水电机组轴系故障划分成正常、轻微不对中、轻微不平衡、轻微碰摩、严重不对中、严重不平衡以及严重碰摩(下文简称为“Nor”、“IMis”、“IIB”、“IRub”、“SMis”、“SIB”以及“SRub”)7种不同状态的信号。从图8中可以看出，论文利用电涡流传感器采集2个径向相垂直(下文简称X和Y方向)的振动信号，采样频率为2048 Hz，共收集各种状态样本共630个，每个样本持续时间2 s。

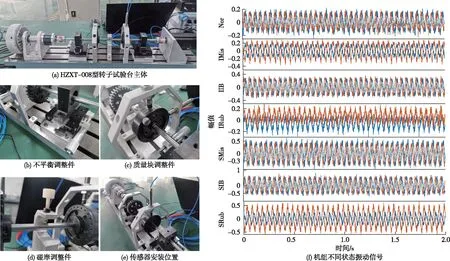
图8 HZXT-008型转子试验台

3.3.1 故障提取特征 受篇幅影响，本文仅分析了RCMMSDE和MMSDE在转子故障试验台的应用。同时，通过比较多元振动信号和单一振动信号的故障特征分布情况，探究多元振动信号融合的必要性。图9给出了不同通道振动信号的特征可视化结果，图9(a)—(c)中可以看出多通道融合的RCMMSDE模型有效区分了7种不同状态的振动信号，而采用X方向振动信号提取的特征中“Nor”和“IMis”故障发生了严重混杂现象，采用Y方向振动信号提取的特征中“IIB”和“SMis”故障存在混杂。此外，图9(d)—(f)给出了MMSDE和MSDE模型特征可视化情况，发现采用单一通道振动信号的MSDE发生了严重混杂，进一步说明了融合多元振动信号的必要性。

图9 不同振动信号特征可视化结果

3.3.2 模式识别 将3.3.1节中提取的特征输入SCN进行模式识别，并采用5折交叉法划分训练集和测试集，每个模型独立运行10次，采用图表的形式评价不同模型的性能。如图10所示，RCMMSDE-SCN模型仅有一个“SIIB”故障被误诊为“IIB”故障，基于X方向振动信号的RCMSDE-SCN模型中有4个“IMis”被误诊为“Nor”信号，基于Y方向振动信号的RCMSDE-SCN模型“IIB”、“SMis”以及“SRub”等故障发生了一定混杂。综合6种模型的混淆矩阵图，表明基于多元振动信号的RCMMSDE-SCN模型具有良好的诊断效果。

图10 不同模型混淆矩阵图

采用诊断率的均值和标准差两个指标衡量不同模型的诊断性能，结果如表4所示，基于多元振动信号的RCMMSDE-SCN模型取得了99.17%的最高诊断率，相比于单一通道(X、Y方向)的RCMSDE-SCN模型提高了2.94%和2.42%的诊断率。同时，RCMMSDE-SCN模型诊断的标准差仅为0.72，验证了所提模型识别故障的稳定性。此外，对比MMSDE-SCN和单一通道(X、Y方向)的MSDE-SCN模型，同样验证了融合多元传感器振动信号可以有效提高模型的诊断性能。

表4 不同传感器振动信号的诊断情况

4 结论

针对现有水电机组轴系故障诊断研究难以兼顾多元传感器信号故障信息的情况，提出了一种基于RCMMSDE和SCN相结合的水电机组轴系故障诊断方法。通过仿真实验分析得出以下结论：

(1)针对水电机组故障诊断中噪声干扰因素的影响，本文采用RCMMSDE进行特征提取，通过分析染噪前后轴心轨迹的熵值曲线相关系数，得出采用RCMMSDE的相关系数为100%、100%、99.97%、99.26%以及95.01%，说明RCMMDSE具有良好的抗噪性能。

(2)采用T-SNE可视化不同多元多尺度熵的特征分布情况，得出采用RCMMSDE模型可以实现不同故障特征的有效提取。将提取到的特征输入SCN模型中进行故障识别，结果表明本文所提方法在两个故障数据集上取得了97.58%和99.17%的最高诊断率，验证了RCMMSDE-SCN模型在水电机组多元传感器故障识别领域具有一定的优势。

(3)通过对比所提模型在单一传感器和多元传感器振动信号的识别情况，得出在MaFaulDa机械故障数据集上采用多传感器振动信号的RCMMSDE-SCN相对于单一传感器振动信号的诊断模型提升了14.98%、11.62%以及1.94%的诊断率，而在HZXT-008型转子故障数据集上采用多元传感器振动信号的RCMMSDE-SCN相对于单一传感器振动信号的诊断模型提升了2.94%和2.42%的诊断率，进一步说明了融合多元传感器故障信号的必要性。

所提方法为融合水电机组多元传感器振动信号进行故障诊断提供了一种新方法，但受实验条件限制，本文仅从振动信号出发，并没有收集到水电机组温度、尾水管压力脉动等可能导致机组不稳定因素的数据，无法从多源角度进行水电机组故障诊断。因此，在后续研究中希望进一步探究融合多源故障因素下多元多尺度熵在水电机组故障诊断中的应用。