基于上海软土模型暗挖法隧道施工的力学特性

苏玥， 叶斌

(同济大学土木工程学院， 上海 200092)

随着城市中心城区的开发强度日益增大，在交通和建筑密集区域建设轨道交通车站面临着越来越突出的环境问题。传统的明挖法对地面交通、市民生存环境、既有市政管线等有较大影响，而暗挖法有环境污染轻、拆迁量小、交通干扰少等优点，更适用于闹市区[1]，但暗挖法用于轨道交通车站的修建时对开挖土体的自立性及稳定性要求较高。以上海为代表的大都市因地下水位较高，土体强度低，属于典型的软土地区[2]，多年来其地铁车站的建设一直采用明挖法，但现如今城市建设与环境、交通的矛盾日益尖锐，明挖法施工遇到瓶颈。因此，在软土地区引入暗挖法建设地铁车站具有十分重要的意义。

管幕暗挖法是近年来逐步推广使用的一种地下暗挖技术。其首先在拟暗挖位置的外周逐根顶进钢管，形成封闭的管幕圈，然后在管幕的围护下进行暗挖施工，最终形成地下空间。管幕暗挖法具有断面灵活、非开挖比例高、施工无噪声振动等优点，但在还未应用于建设上海软土地铁车站工程。因此，上海市以轨道交通14号线桂桥路站为试点工程，尝试将管幕暗挖法实践于上海软土地层中。

管幕暗挖法的施工工序较为复杂，管幕的设计方案、顶进顺序尤为重要，同时，在管幕支护下的暗挖法施工方案、工艺技术也将直接影响施工扰动程度。因此，针对管幕暗挖工程开展精细化的数值模拟研究，有助于掌握此类工程的力学行为特征，防范施工风险。数值模拟是进行工程力学性质研究的一种重要手段，许多学者已对暗挖法隧道施工进行过数值模拟工作，深入研究了暗挖法工程的力学特性。陈功祥等[3]建立了Midas-GTS NX三维模型，进行了深回填土区暗挖隧道群力学特性的数值模拟研究；牛斌等[4]采用注浆试验，采用FLAC3D数值分析与现场监控量测相结合的方式研究粉细砂地层单层暗挖车站柱洞法施工时地表沉降规律，并提出了一种在粉细砂地层单层暗挖车站的优化设计方案；戴亚军等[5]采用数值模拟计算方法对超大断面泥质粉砂岩地铁车站浅埋暗挖施工的开挖方法及支护结构进行了优化研究，分析了不同开挖和支护方案下的拱顶位移，地表沉降和支护结构受力情况；梅源等[6]基于实测数据及数值模拟，研究了湿陷性黄土地区富水砂层冻结法暗挖施工的土体温度场，应力场及冻胀融沉规律；杜俊等[7]采用有限元数值模拟方法，模拟在不采取预加固措施时暗挖地下通道的施工过程；雷啸天等[8]利用FLAC3D验证了数值模型的正确性，同时模拟了围岩在真实时间下的施工力学响应；文献[9-10]利用数值模拟方法对隧道变形进行了研究，提出了合理的变形控制措施。这些研究涉及的地层多为砂土、卵石或岩层等较为稳定的地层，且现有的数值分析一般采用Mohr-Coulomb、Drucker-Prager、Duncan-Chang等经典本构模型。这些本构模型虽然应用比较广泛，但仍存在无法考虑土体结构性、超固结性和各向异性等特征的缺点[11-12]。因而，对于饱和软土地层的轨道交通车站的暗挖法施工需进一步研究，同时也需要探索更加合适的本构模型来研究其力学特性。

上海地处长江口南岸平原区，成陆较晚，全区地势平坦，第四纪地层十分发育，上海地区地层结构可以分为两部分，下部埋深145～320 m，是杂色黏土与砂砾互层，为早更新世陆相沉积物；上部是以灰色为主，夹有黏土，与浅灰、黄灰色粉砂性土互层，称为“灰色层”，属中更新世以来海陆沉积物，故上海饱和软土具有独特的性质。上海软土模型是在剑桥模型基础上发展的精细化本构模型，模型采用的参数更能反映上海地区软土的三大特点，即超固结性(长江冲积和海进海退的共同作用)、结构性(顶部和底部是超固结硬壳层，中间是灵敏软黏土)和各向异性(重力沉积作用导致颗粒形态和孔隙微观结构在空间取向上的差异性)[13-16]。现将此精细化本构模型用于桂桥路车站施工数值模拟中，分析基于上海软土本构模型的暗挖法隧道施工位移、应力、应变等力学特性，为相关工程提供参考和借鉴，有利于加快暗挖工法技术体系在软土地层中心城区复杂环境地铁车站建设中的形成。

1 工程概况

上海市轨道交通14号线桂桥路站附属结构段(图1)位于上海市浦东新区王家桥路与曹家沟交界处，下穿曹家沟，覆土厚度约7.1 m。此结构段采用暗挖管幕法施工，暗挖管幕段长度为100 m，暗挖埋深约5.4 m。结构为地下一层钢筋混凝土箱涵结构，结构外包尺寸为宽21.99 m，高7.2 m，净宽20.19 m，净高5.4 m。暗挖管幕段横断面示意图如图2所示。

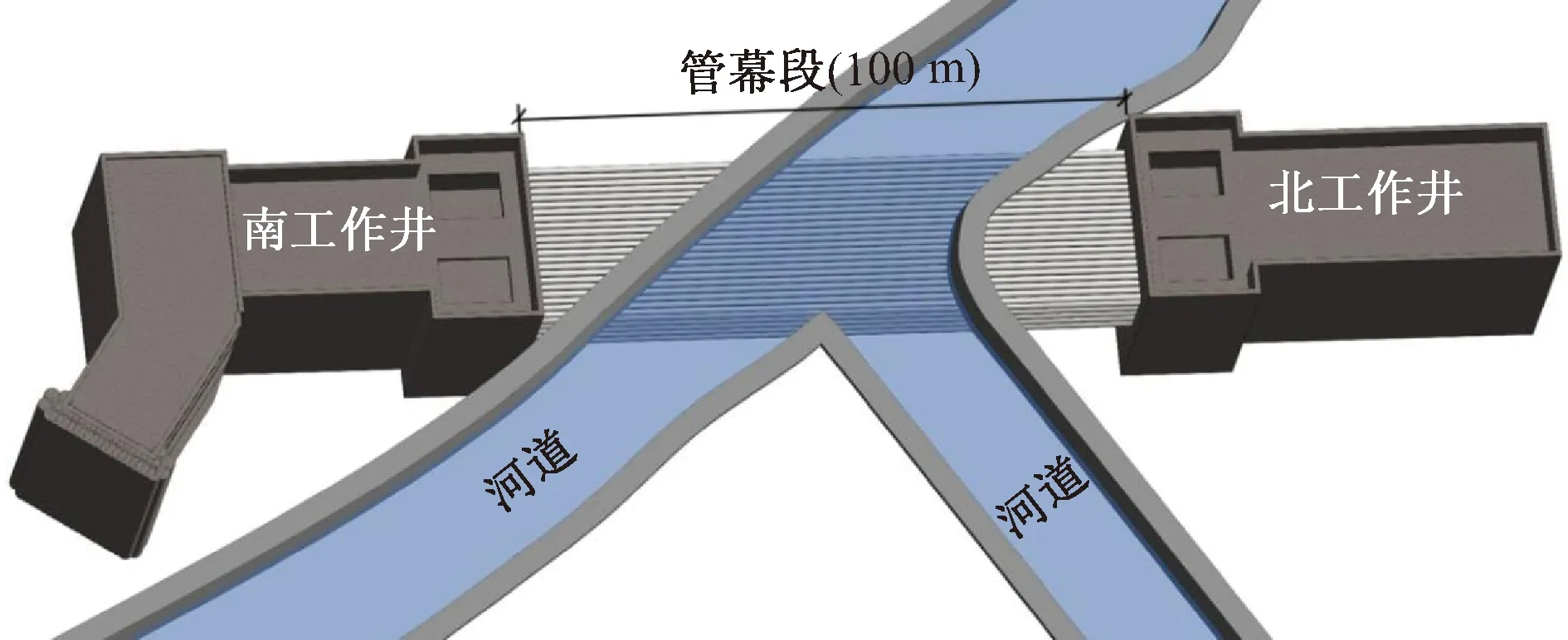
图1 暗挖管幕段平面效果图Fig.1 Plane rendering of underground pipe curtain section

1.1 施工工法

施工时首先采用顶管机在暗挖位置的外周逐根顶进52根钢管[图3(b)]，形成封闭的水平管幕；然后采用水平全方位高压喷射(metro jet system，MJS)工法桩对开挖掌子面进行加固[图3(c)]，前30 m满仓加固，为强加固区，剩余70 m跳仓加固，为弱加固区)，以防掌子面失稳、倾覆；其次进行管幕间冻结加固，使管幕形成密闭的帷幕；接下来采用台阶法分仓分层开挖土体；待全部开挖完成后，进行主体结构施工[17]。

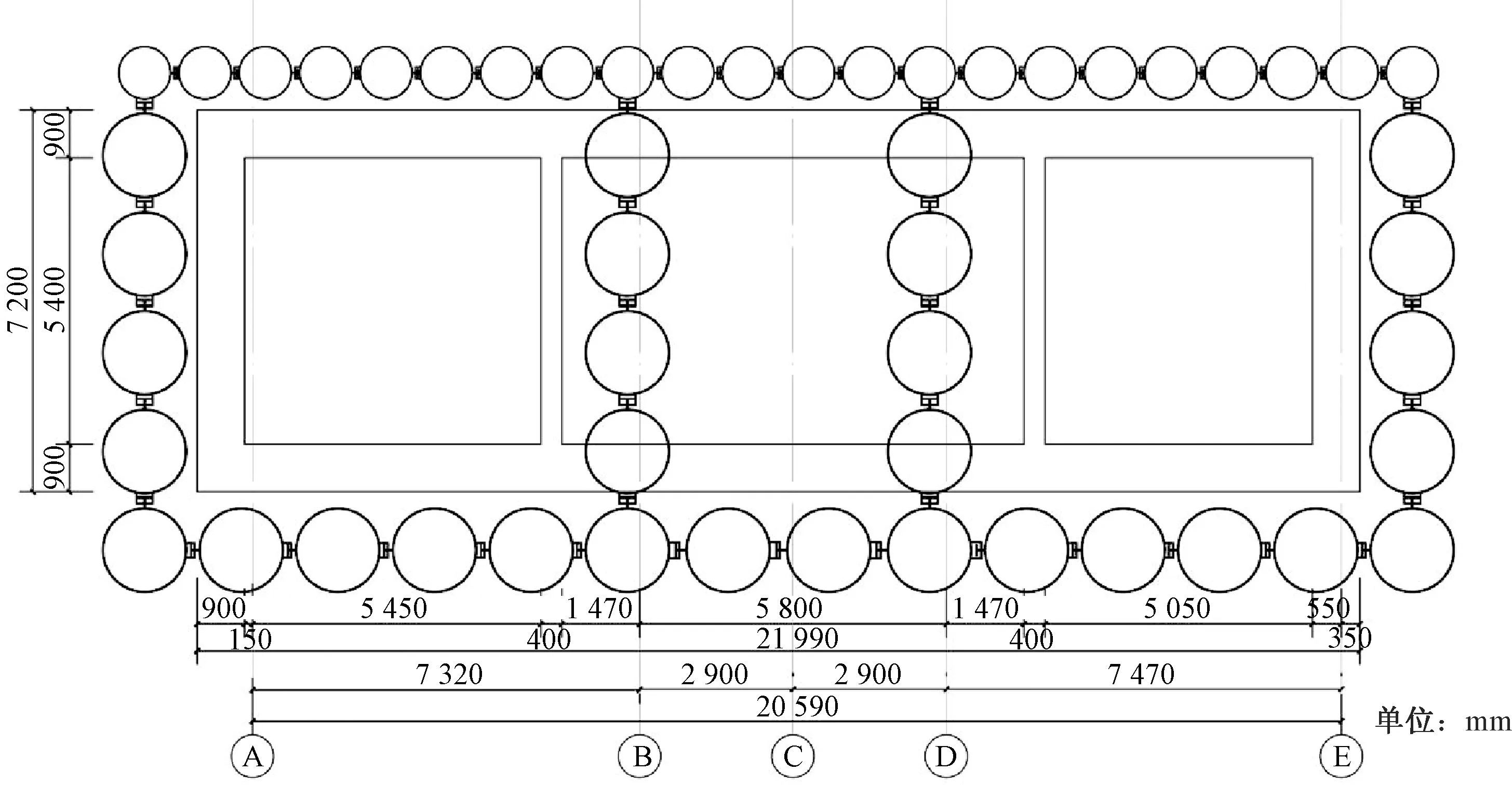
图2 暗挖管幕段横断面示意图Fig.2 Diagraph of cross section of underground pipe curtain section

图3 管幕试验段示意图Fig.3 Schematic diagram of tube curtain test section

因管幕横向无约束，进行全断面开挖风险极大。故暗挖断面开挖的基本原则为：分仓、分层、短进尺、及时支撑。为减小开挖期间沉降变形，同时考虑施工过程安全性和便利性，管幕段土方开挖的总体流程为：从北向南，先上后下，先左右后中间。根据此流程，开挖顺序如图4所示。具体开挖方案为：1仓→2仓→3仓→4仓→5仓→6仓。

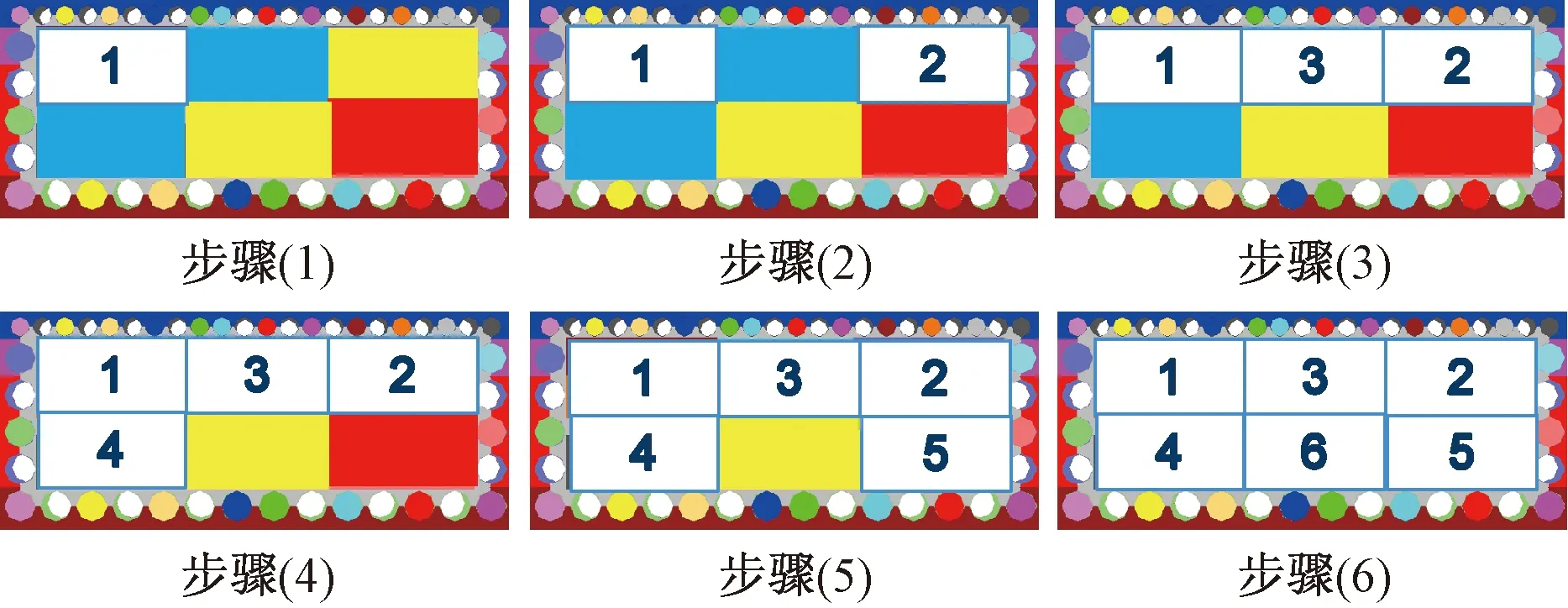
图4 各仓开挖顺序Fig.4 Excavation sequence of each warehouse

1.2 工程地质条件

勘察结果表明，工程场地属于上海市正常地层分布区域，沿线场地80 m深度范围内地基土自上而下为：第①1层杂填土，第②层褐黄～灰黄色粉质黏土，第③层灰色淤泥质粉质黏土，第③夹层黏质粉土，第③层灰色淤泥质粉质黏土，第④层淤泥质黏土，第⑤1层灰色黏土，第⑥层暗绿～草黄色粉质黏土，第⑦1-1层黏质粉土夹粉质黏土。管幕顶进的土层主要为③层灰色淤泥质粉质黏土和④层淤泥质黏土中，均为饱和、低强度、高压缩性的土层。各土层的厚度及物理力学参数如表1所示。

2 上海软土模型理论及参数取值

2.1 有限元软件DBLEAVES简介

采用自行研发的有限元软件DBLEAVES模拟暗挖法隧道施工。DBLEAVES是地基-基础-上部结构一体化静力与动力有限元分析程序。该程序能高效进行二维和三维水土耦合数值计算，可用于计算静力和动力问题。该程序包含可用性强的精细化本构模型，例如循环流动模型(cyclic mobility model，CMM)等，运算能力强大，适合用于解决各类岩土工程问题。DBLEAVES解析流程如下：开始→剖分网格并确定材料参数→制作输入文件→运行DBLEAVES程序→整理计算结果→结束。

表1 地层的物理力学参数Table 1 Physical and mechanical parameters of formation

2.2 上海软土模型理论

CMM是基于剑桥模型发展起来的一种精细化本构模型，在剑桥模型的基础上考虑了软土的超固性、结构性和各向异性特征，因而更能反映上海软土的特点。对CMM本构模型进行简要介绍，具体推导过程可参阅相关文献[13-16]。

2.2.1 屈服面方程

CMM也是一种弹塑性本构模型。该模型的屈服面函数与修正剑桥模型类似，采用正常固结屈服面、上负荷屈服面以及下负荷屈服面来描述土体正常固结应力状态、结构应力状态和超固结应力状态，如图5所示。

pm为下负荷屈服面与各向异性转轴交点在轴上的投影，坐标点对应为为正常固结屈服面与各向异性转轴交点在轴上的投影，坐标点对应为为上负荷屈服面与各向异性转轴交点在轴上的投影，坐标点对应为图5 CMM在p-q平面上的屈服面Fig.5 Yield plane of CMM in p-q plane

R*为上负荷屈服面和正常固结屈服面间相似比，R为上负荷屈服面和下负荷屈服面之间的相似比，如式(1)和式(2)所示。

(1)

(2)

下负荷屈服面如式(3)所示。

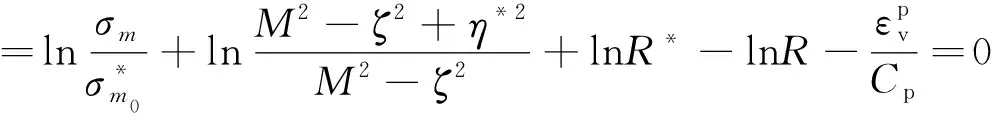
(3)

式(1)、式(2)和式(3)中的参数详细说明如下。

(4)

(5)

(6)

(7)

2.2.2 应力诱导各向异性应力张量

应力诱导各向异性应力张量发展准则表达式为

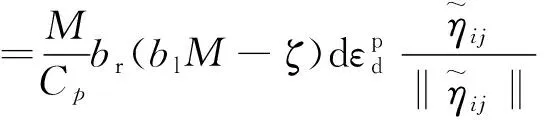
(8)

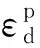
2.2.3 结构参数

结构参数R*发展准则表达式为

(9)

其中U*表示为

(10)

式(10)中：a为控制剪切过程中结构消散速率的参数。

2.2.4 超固结参数

超固结参数R的发展准则定义为

(11)

(12)

(13)

式(13)中：m为控制超固结状态变化的材料参数。

2.3 参数取值

CMM的②～⑥层土参数已有学者进行了研究[18-19]，结果显示模拟结果与试验结果吻合程度较高，说明确定的参数可用于工程计算。第⑥层以下土体参数首先根据勘察报告获得各土层对应的重度γ、静止土压力系数K0以及渗透系数k值；然后，通过固结试验得到模型中所需要的第⑧层和第⑩层土的参数取值；最后，利用CMM模型对深层土固结不排水三轴试验进行模拟得到其余参数的取值。现将所有土层参数汇总于表2和表3。

3 桂桥路车站数值模拟及结果分析

3.1 计算模型

采用三维模型来模拟土体开挖，如图6所示。土体模型水平方向尺寸为85.6 m，竖向36 m，纵向100 m。钢管群简化为墙体，土体、钢管群与MJS加固体均采用六面体实体单元模拟，开挖部分开挖进尺为12.5 m分割。模型除顶面外均采用法向约束，地表为自由边界，荷载仅考虑所有单元的自重。周围土体采用精细化本构模型CMM，钢管群与MJS加固体采用弹性本构模型，土体的计算参数如表4所示，钢管群、MJS加固体的计算参数如表5所示。划分网格时遵循如下原则：开挖处和钢管群处网格划分尽量密集，越接近模型边缘，网格划分越稀疏。

表2 CMM参数汇总1Table 2 CMM parameter summary 1

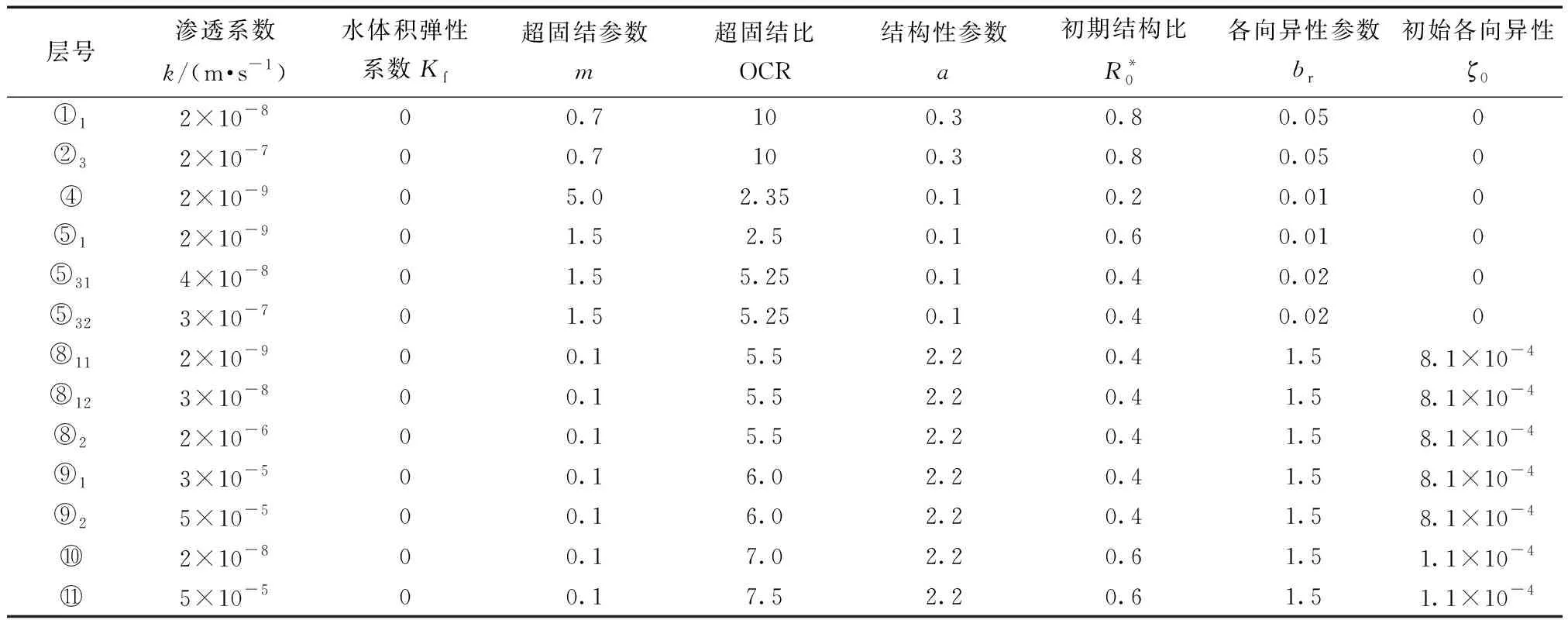
表3 CMM参数汇总2Table 3 CMM parameter summary 2

模型首先进行弹性计算，使土体达到施工前的固结状态，并形成初始应力场。由于此部分主要模拟管幕内主体部分的开挖，因此将钢管群简化为墙体，并简化钢管群与MJS加固的施工过程，即在一个分析步内完成钢管群的安放及MJS加固，不模拟支撑部分。MJS加固体均为强加固。至此，主体部位开挖前的模型已建立完毕，再次对模型进行位移清零，以方便查看开挖及支撑引起的地层响应。接下来按照施工规划，依次开挖。

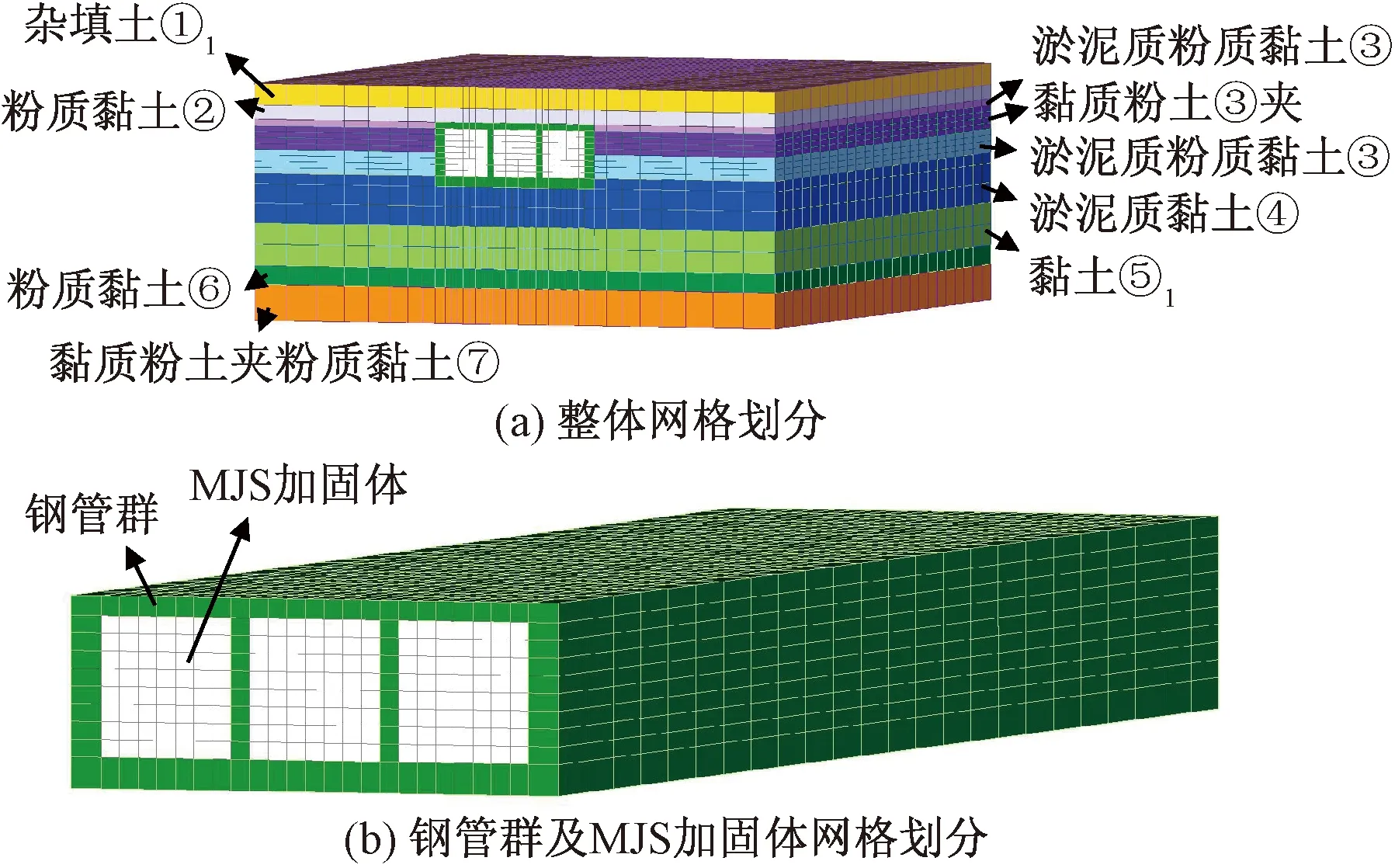
图6 三维模型网格划分Fig.6 3D model meshing

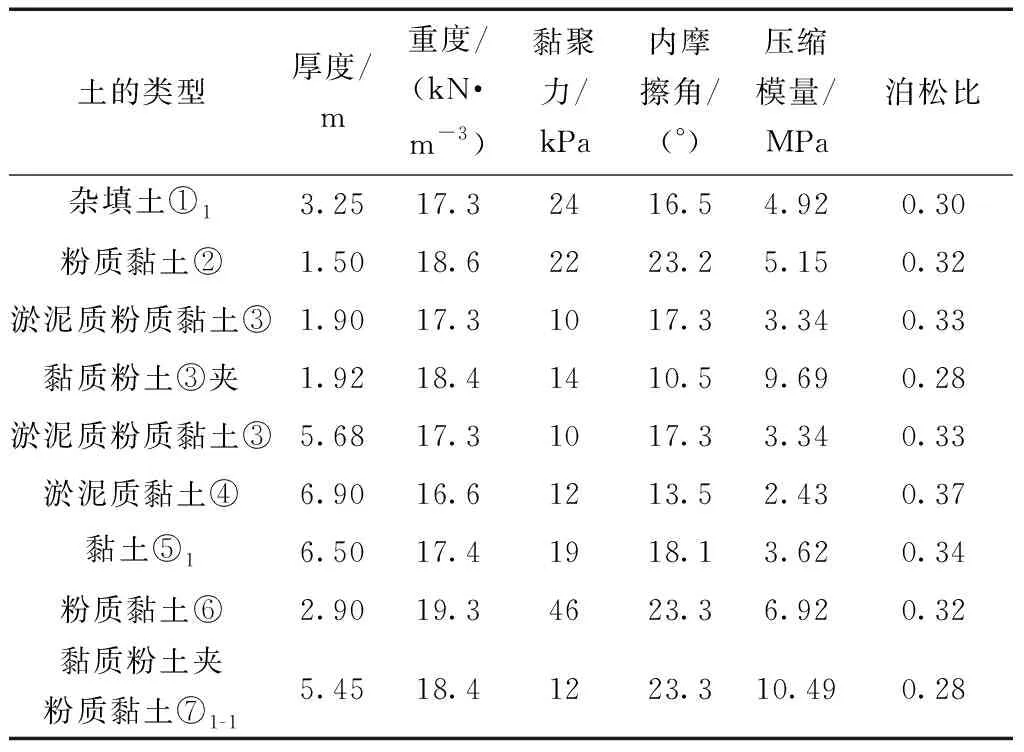
表4 地层的物理力学参数Table 4 Physical and mechanical parameters of formation

表5 钢管群及MJS加固体的计算参数Table 5 Calculation parameters of steel tube group and MJS plus solid

模拟的施工方案为上台阶先开挖，下台阶后开挖。对于上台阶或下台阶都是左右两仓先开挖，中间仓后开挖，即开挖顺序为：1仓→2仓→3仓→4仓→5仓→6仓(如图4所示)。每步开挖前进12.5 m。每开挖12.5 m为一个分析步，开挖6个仓总共需要48个开挖步，即整个施工过程共48个工况载荷步。

3.2 计算结果分析

3.2.1 位移场分析

1)竖向位移

在隧道施工前，分析因隧道开挖而产生的地表位移情况对于施工的安全保障具有指导作用。图7为6个仓开挖过程中的地表变形曲线，可以看出，地表主要发生了沉降变形。1仓开挖引起的最大地表变形最小，变形最均匀。2仓开挖后，地表变形呈对称性，这是由于开挖呈对称性；同理，4仓开挖后，左仓上方地表变形偏大，待6仓开挖完之后，变形再次具有了对称性，最终地表变形趋于对称分布。由此可推知，连续开挖两侧仓的上下台阶会加大地表不均匀变形，先分别开挖两边仓的上下台阶再挖中间仓可减小地表不均匀变形。

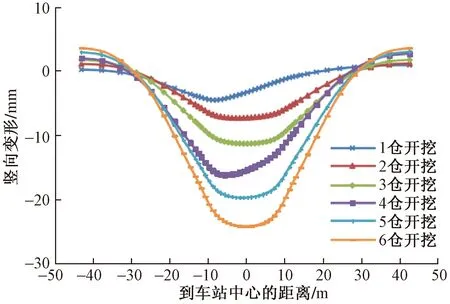
图7 开挖过程中地表变形曲线Fig.7 Surface deformation curve during excavation

由于岩土介质的多相性及边界条件的复杂性，单纯的数值模拟和理论分析均不能准确分析隧道施工过程中围岩的力学行为，而现场监控量测不仅能及时反馈信息指导设计和施工，还能弥补数值模拟和理论分析等研究手段的不足，为此，选取开挖完毕后现场实测位移数据进行分析。在桂桥路车站施工现场，每隔5～6 m布设一个地表沉降监测点。图8中的实测位移曲线为开挖完成后，实测的地表变形曲线。由该曲线可知，地层发生了较大的沉降变形，最大值可达27 mm。与选用Mohr-Coulomb本构模型对暗挖法施工过程的模拟[20]对比，运用CMM本构模型的模拟结果更加接近实测值，这是由于上海软土模型采用的参数更能反映上海地区软土的超固结性、结构性、各向异性等三大特点。

隧道工程的施工使得周围土体发生了显著的变形，但影响范围是有限的，即超过一定的距离以后可忽略对土体变形的影响。图9为开挖过程中钢管群底部水平面的变形曲线，结果表明，开挖底部表面竖向位移较小，最大竖向位移为0.018 mm，钢管群下方表面竖向位移最小，最小值为0.01 mm。值得注意的是，越靠近钢管群处土体越有向上隆起的趋势，主要原因是管幕埋深较浅，且顶管挤土效应比较严重，同时，受上部土体开挖的影响，隧道底部土体应力得到释放，进一步解释了开挖卸荷造成的隧道底部隆起。

图10 开挖过程竖向位移分布云图Fig.10 Cloud diagram of vertical displacement distribution during excavation

图8 开挖完毕后地表变形曲线Fig.8 Surface deformation curve after excavation

典型开挖步的土体竖向方向位移如图10所示。从第一步开挖起，竖向位移最大值出现在中心附近。1仓开挖后竖向最大位移为4.7 mm，2仓开挖后最大位移为7.6 mm，3仓开挖后的最大位移为11.7 mm，4仓开挖后的最大位移为16.9 mm，5仓开挖后的最大位移为20.5 mm，6仓开挖后的最大位移达到了25.2 mm。不同仓开挖时地表变形具有相同的分布规律，最大变形发生位置基本保持在车站中心的位置，故在设计和施工时应考虑在车站中心位置加强支护，避免发生坍塌现象。此外，在隧道施工过程中，地表的变形明显大于下方，表明隧道施工对其上方土体的扰动更加明显，在浅埋隧道中宜加强地表位移的监测，评估对其影响范围内建筑物的安全。

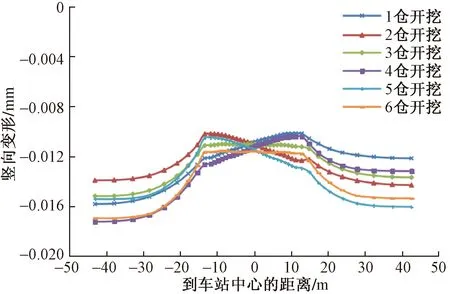
图9 开挖过程中钢管群底部水平面变形曲线Fig.9 The horizontal plane deformation curve of the bottom steel tube group during excavation

2)水平位移

为便于叙述，将模型各部位进行定义，如图11所示，分析开挖过程中隧道周围土体的水平位移随关键计算步变化(图12)，可以看出：受左右仓土体开挖步序来回切换的影响，隧道周边土体的水平位移变化也呈现了一定的跳动现象。左肩和右肩的水平位移基本一致，最大水平位移发生在肩部，在1仓开挖和4仓开挖时水平位移最大，约为0.5 mm，其他部位的水平位移较小，约为0.1 mm。总体来看，开挖过程中水平位移较小，所以开挖后隧道围岩位移以竖向位移为主，为保证隧道安全，应重点控制隧道的竖向位移。需要注意的是，虽然隧道周围土体水平位移较小，但可能会因左右仓开挖步序转换而出现日均水平位移变化幅度过大的问题，这点应引起工程上的重视。

图11 模型各部位定义Fig.11 Definition of each part of the model

3.2.2 应力分布规律

图13 剪应力分布云图Fig.13 Cloud diagram of shear stress distribution

从力学角度来看，隧道的开挖和支护是不断地加、卸载的过程，同时也使得围岩的边界条件不断改变。围岩内部在开挖过程中，应力状态不断改变和调整，因此会产生相应的变形甚至是破坏。开挖完毕后的剪应力分布云图如图13所示，可以看出，剪应力沿隧道开挖断面分布趋于均匀，在左脚和右脚部位产生应力集中，最大剪应力达到94.8 kPa，其次是左肩和右肩部位。由于土体的抗剪性能差，因此在开挖过程中，考虑将底脚附近作为隧道围岩破坏判定的关键位置，故开挖过程中应注意在底脚部位加强支护。

3.2.3 应变分布规律

隧道开挖后，围岩往往由于变形过大而产生拉剪或是压剪破坏，剪应变能较好反映围岩受到工程力的变形或是破坏。图14为典型开挖步对应的剪应变云图，可以看出，开挖过程中，周围土体的剪应变基本呈对称分布，剪应变一直集中分布在左肩和右肩部位，表明肩部是开挖时的薄弱部位，局部塌方风险极高，在开挖前建议着重对肩部进行MJS加固。

4 结论

介绍了上海软土本构模型，依托桂桥路车站工程，将此精细化本构模型用于桂桥路车站暗挖法施工数值模拟中，研究了基于上海软土本构模型的暗挖法隧道施工力学特性。主要结论如下。

(1)开挖阶段地层主要发生了沉降变形，沉降值与现场实测值较接近。不同仓开挖时地表变形曲线具有相同的分布规律，最大变形发生位置基本保持在车站中心的位置，开挖完毕后地表变形达到最大，最终地表变形趋于对称分布。

(2)开挖完毕后，横断面上的剪应力分布呈现对称性，在开挖土体左脚和右脚部位易产生应力集中，由于岩土介质的抗剪性能差，沿底脚这一路径易发生破坏，故开挖过程中应注意在底脚部位加强支护。

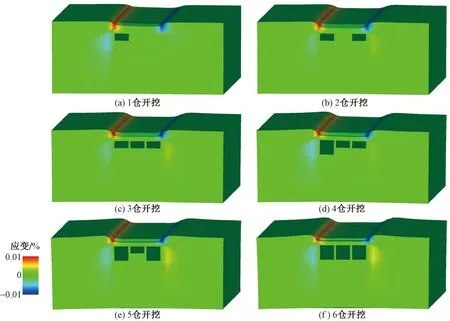
图14 开挖过程剪应变分布云图Fig.14 Cloud diagram of shear strain distribution during excavation

(3)开挖过程中，开挖土体周围的剪应变基本呈对称分布，开挖土体上方主应变最大，表明开挖过程中上方土体易发生破坏，其中，左肩及右肩局部塌方风险极高，在开挖前建议着重对肩部进行MJS加固。

(4)与选用Mohr-Coulomb本构模型对暗挖法施工过程的模拟进行对比，运用上海软土模型的模拟结果更加接近实测值，这是由于上海软土模型采用的参数能更好地反映上海地区软土的超固结性、结构性、各向异性等三大特点。

(5)将上海软土本构模型用于桂桥路车站的开挖施工模拟中，从计算结果看，与实测数据规律基本一致，但由于此本构模型较为复杂，针对大型工程的模拟仍存在计算速度较慢等问题，后续将进一步研究提高计算速度的方法。