基于支持向量机的输气管道泄漏压降信号智能识别方法

贾文龙，孙溢彬，汤丁，陈家文，雷思罗，李长俊

（1 西南石油大学石油与天然气工程学院，四川 成都 610500；2 重庆相国寺储气库有限公司，重庆 401121）

为保证输气管道安全运行，根据标准GB 50251《输气管道工程设计规范》的要求，需要在管道沿线设置截断阀室。目前国内大多数管线采用美国Shafer气液联动阀，当气液联动阀检测到的管道压降速率和持续时间同时超过设定值时，截断阀将自动关断。如表1所示，国内不同管线的截断阀参数设定值存在一定差异，大部分设置压降速率为0.15MPa/min，持续时间为120s。

表1 截断阀参数设定值

然而，在实际情况中采用上述设定值后，截断阀仍会出现无法在管道泄漏时正常关断的情况。例如，2012年西部某天然气管道发生约20mm的小孔泄漏，检测的压降速率约0.03MPa/min，截断阀没有自动关断；2015 年中石油天然气管网发生多起泄漏事故，由于泄漏量和检测的压降速率较小，所有事故中截断阀均未自动关断。

国内外学者针对如何合理设置阀门压降速率和持续时间的问题开展了大量的研究。Zuo 等分析了持续时间为120s时泄漏工况对压降速率的影响，表明管道的最大压降速率与管道运行压力成正比，与气体流速成反比。杨毅等模拟了不同泄漏工况对截断阀压降速率和持续时间的影响，发现小于300mm的泄漏孔径几乎不会引起截断阀自动关断。赫德明等针对安徽省某输气管道提出了气液联动阀的压降速率与持续时间的推荐值，但仅能截断泄漏孔径为200mm以上的泄漏情况。贾文龙等基于仿真将压缩机抽吸工况和泄漏工况的压降信号进行对比，研究发现这两种工况的压降速率有重复，容易引起截断阀的不关断或误关断。因此，气液联动阀检测管道泄漏目前存在两方面的问题：首先是管道发生小孔径泄漏时的压降速率远小于设定值，致使截断阀无法自动关断；其次是压缩机的抽吸等正常运行工况也会导致管道的压力下降和波动，如果试图降低设定值以识别出更小的泄漏工况，就会引起截断阀在管道正常运行时的误关断。为此，研发新的泄漏压降速率信号识别方法有助于提升气液联动阀对泄漏工况以及其他工况的判断能力与执行能力，确保管道平稳供气。

近年来，随着智慧管道的发展，人工智能的检测方法越来越受到关注，它主要通过对采集的压力信号、流量信号或声信号进行实时特征值提取与分析来实现管道泄漏的检测。焦敬品等基于声信号的特征参数构建了BP 神经网络管道泄漏识别系统，实现了不同泄漏信号的交叉识别。张瑞程等基于声信号的特征参数，基于一维卷积神经网络提出了一种泄漏识别模型，优化了输气管道泄漏识别中的数据预处和特征提取过程，提高了识别的准确率。郝永梅等对总体局域均值分解与多尺度熵进行改进，提出了一种管道泄漏识别方法，减少了分解后的误差，提高了泄漏信号的识别率。逯雯雯将布谷鸟和粒子群算法进行融合并优化了支持向量机的参数，根据负压波信号的特征建立了二叉树多分类支持向量机模型，实现了对泄漏点的定位。Ning等将频谱增强和卷积神经网络相结合，提出了一种天然气管道泄漏检测方法，该方法可以增强泄漏信号并降低背景噪声。Zadkarami 等使用统计技术和小波分析的方法，提取了泄漏管道的进口压力和出口流量等信号特征，使用多层感知器神经网络进行分类，实现了对泄漏位置和泄漏尺寸的识别。Li等提出了一种基于核主成分分析和支持向量机的声信号泄漏检测方法。Liu 等采用滤波法对声信号进行处理，提出了信号去噪系统和泄漏点定位方法，提出的系统能够有效地从实测信号中提取泄漏信号且泄漏检测结果的精度也较高。Diao等结合粒子群算法和最大熵原理对声波信号进行重构，基于变分模态分解提取了声波信号的特征，通过支持向量机对管道泄漏进行检测。

然而，国内外研究大多以声波信号为研究对象，目前还缺乏压降速率信号对管道泄漏识别的研究与验证。因此，考虑气液联动阀的检测特点并结合实际工程中截断阀遇到的问题，基于相国寺储气库输气干线数据，建立并验证管道压降速率仿真模型。通过模型获得管道泄漏、压缩机抽吸以及截断阀紧急截断工况的压降速率信号然后进行特征分析。改进教与学优化算法并用其优化支持向量机内的参数，建立多分类的支持向量机泄漏信号识别模型，以期提供一个快速且准确的管道泄漏智能识别方法。

1 压降速率信号的采集

1.1 压降速率的计算

Shafer 气液联动阀的对点检测压降速率计算如式(1)～式(3)所示。

式中，p为时刻的平均压力，MPa；为时刻的压力，MPa；为-5s 时的压力，MPa；为-10s 时 的 压 力，MPa；为-15s 时 的 压 力，MPa；为-20s时的压力，MPa。

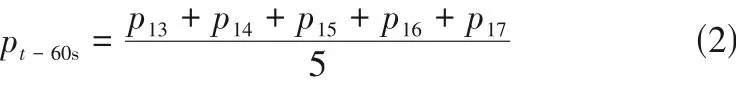
式中，p为-60s 时的平均压力，MPa；为-60s 时的压力，MPa；为-65s 时的压力，MPa；为-70s 时的压力，MPa；为-75s 时的压力，MPa；为-80s时的压力，MPa。

式中，ROD为时刻的压降速率，MPa/min。压力曲线见图1。

图1 压力曲线

1.2 压降速率信号的模拟

如图2所示，相国寺储气库铜相线全长84.2km，设计输量2100×10m/d，设计压力10MPa，沿线有5座阀室，集注站内设有压缩机组，在注气阶段时启动。采用PipelineStudio 仿真软件建立了铜相线的管道仿真模型，通过现场实测数据对模型进行验证，平均相对偏差为0.38%，验证了模型的可靠性。

图2 相国寺储气库铜相线

基于仿真模型，结合铜相线的实际情况，模拟了管道泄漏、压缩机抽吸和截断阀紧急截断3种工况下集注干线上各阀室的压力变化情况。为了使数据更具多样性，模拟了不同边界条件在任意组合下对阀室压降速率的影响，其中管径为660～1016mm、输量为(300～2100)×10m/d、压力为5～10MPa、泄漏孔径为25～125mm、泄漏位置为两阀室间10%～70%的位置、压缩比为1.5～3.0。

以土场阀室为例，图3 为该阀室在相同输量、压力等边界条件下对应3 种不同工况时的压力曲线。其中泄漏工况的泄漏孔径为80mm，泄漏位置为两阀室间70%位置；压缩机抽吸工况的压缩比为2.5；截断阀截断工况为静观阀室突然截断后土场阀室的压力变化情况。以上所有动态工况均发生在第3分钟，共持续30min。

图3 不同工况下阀室压力曲线

根据式(3)将压力信号转化为压降速率信号。图4(a)显示，同一阀室在不同泄漏孔径下，压降速率信号趋势保持一致，但泄漏孔径越小，信号的波动越不明显。由于压力波动会随着传播距离增大而减弱，所以在图4(b)、(c)可以看到，这两种工况下距离集注站或静观阀室（紧急截断的阀室）越远的阀室，压降速率越小且信号越加平缓。纵观图4，这3种工况的某些压降速率信号在数值上相近，这也是截断阀误关断或不关断的主要原因，因为气液联动阀单一地根据压降速率数值无法准确区分出这些工况。但观察发现，不同工况下压降速率信号曲线的趋势各有不同，而机器学习就可以根据这些曲线的特征来反向判别该信号所属的工况类别，进而指导截断阀是否动作。

图4 不同工况下阀室的压降速率曲线

2 泄漏信号的智能识别模型

2.1 支持向量机模型

支持向量机（support vector machine，SVM）属于机器学习模型的一种，近年来被广泛应用于模式识别领域中的数据分类问题。SVM的目标是找到一个分类超平面，使训练集中的点尽可能远离它。实际情况中大部分的分类问题为线性不可分问题，在解决这类问题时SVM 中的核函数可以将样本数据从原始空间映射到高维空间，使原始的样本数据在高维空间中转变为线性可分的情况。实际情况中，管道泄漏属于小概率事件，能够采集到的压降速率信号样本有限。而支持向量机恰好适用于解决小样本、非线性的分类问题，在管道泄漏识别领域具有一定的优势。非线性分类问题的分类超平面的表达式如式(4)所示。

2.2 TLBO算法的优化

支持向量机在处理分类问题时，通常要对其内部的惩罚因子和核函数参数进行优化。相比于粒子群算法和遗传算法，教与学优化算法（teaching-learning-based optimization，TLBO）因其具有更高的寻优精度、收敛速度和参数设置简单等优点而被广泛关注。TLBO 算法模拟了课堂中学生从老师和其余学生处获取知识的过程，学生的成绩（适应度值）在学习过程中不断提高，最终使学生在目标函数处的表现不断接近全局最优值。该算法由教师阶段和学生阶段两个阶段组成。

教师阶段是将每次迭代中成绩最高的学生作为老师，其他同学不断向老师学习进而提高班级平均成绩的过程。该过程的数学表达式如式(5)、式(6)所示。

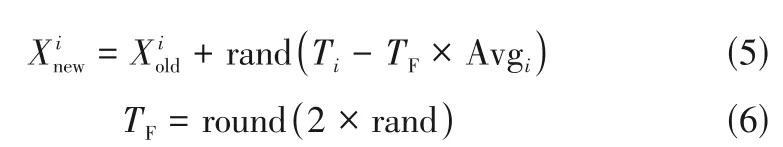
式中，Xn和Xo分别为向老师学习后和学习前的学生个体，为[0,1]间的随机数；为学习因子，取1或2。

学生阶段是两个随机的学生X和X间相互学习的过程，每个学生都能从比自己成绩更好的学生处获得新知识。该过程的数学表达式如式(7)所示。

虽然TLBO算法具有参数少、计算精度高等优点，但是在求解时容易陷入全局最优解。因为TLBO 算法使用随机初始化的方法产生种群个体，使粒子分布不均匀，如果初始种群没覆盖到全局最优解且在有限的迭代次数内没有搜索到最优解，就会导致算法过早收敛、求解精度低等问题。而且TLBO 算法平衡全局搜索和局部搜索的能力较差，容易使算法陷入局部最优解。因此，为进一步提高压降速率信号识别模型分类的准确率，从种群初始化和平衡局部与全局寻优能力两个方面对TLBO算法进行改进。

2.2.1 改进的Tent混沌映射

研究显示，利用混沌映射对种群进行初始化会影响算法的整个过程，而且产生的变量具有较强的遍历性，常常能取得比伪随机数更好的效果。标准的Tent混沌映射如式(8)所示。

式中，Z为第个混沌变量，取值范围为[0,1]；为(0,1)之间的随机数，取0.4。

然而，标准Tent 混沌映射产生的混沌粒子在[0,1]区间内分布仍不够均匀，遍历性还有待提升。因此，对标准Tent 混沌映射进行了改进以提高初始种群粒子的均匀性，如式(9)、式(10)所示。

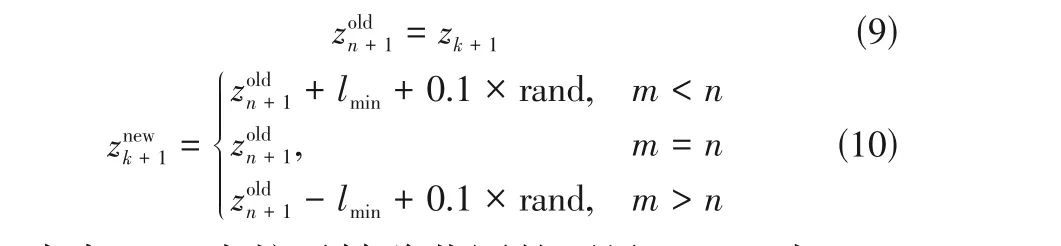
式中，为粒子转移范围的下界；rand为[0,1]之间的随机数。

如图5所示，对比了标准Tent混沌映射和改进的Tent混沌映射，均产生100个混沌变量，将区间按[0,0.1),(0.1,0.2],…,(0.9,1]分为10个区间，统计了粒子在各区间分布的个数。

图5 粒子在各区间分布情况

由图5可以看到，使用改进的Tent混沌映射产生的变量在各区间的分布较改进前的更加均匀，具有更好的遍历性。基于改进的Tent 混沌映射对种群进行初始化的公式如式(11)所示。

式中，为变量的最小值；为变量的最大值。

2.2.2 自适应惯性权重函数

惯性权重的概念在首次提出时就引入了PSO算法中，随后大量研究证明，惯性权重能够很好地平衡算法的全局和局部搜索能力。在此基础上，以最优个体适应度值的更新率和迭代步数作为自变量，提出了自适应惯性权重调节函数，并将其引入到TLBO算法中，具体函数如式(12)、式(13)所示。

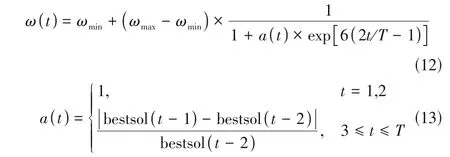
式中，()为第次迭代时的惯性权重；为最小惯性权重，取0.9；为最大惯性权重，取0.1；为最大迭代次数；()为种群最优个体适应度值的更新程度；bestsol(-1)为第-1 次迭代时最优个体的适应度值；bestsol(-2)为第-2 次迭代时最优个体的适应度值。

相应地，式(5)变为式(14)。

当相邻两次迭代最优个体的适应度值变化很小或不变时，算法可能陷入局部最优，增大惯性权重，可以使种群跳出局部最优。从图6 中可以看到，自适应惯性权重函数还保证了算法在迭代前期拥有较大的惯性权重，提高了全局搜索能力，在迭代后期拥有较小的惯性权重，提高了局部搜索能力，有利于种群向最优解逼近。

图6 自适应惯性权重函数曲线

图7为改进的教与学优化算法流程。与改进前的教与学优化算法相比，改进后的算法在种群的初始化阶段使用改进的Tent 混沌映射替代了之前的伪随机数法。同时，在教师阶段和学生阶段的计算公式中，均引入了自适应惯性权重，进一步提升了算法的寻优性能。

图7 改进的教与学优化算法流程

2.3 改进算法的测试结果与分析

为检验改进的教与学优化算法（improved teaching-learning-based optimization，ITLBO）的寻优能力，选用:Sphere、:Sum Square、:Schwefel 2.22、:Ackley、:Griewank、:Rastrigin共6个常用的benchmark 测试函数对算法进行测试，这些函数的理论最小值均为0。将测试结果与使用教与学优化算法、粒子群算法（particle swarm optimization，PSO）和遗传算法（genetic algorithm，GA）的结果进行了对比。所有优化算法的种群大小均为50，迭代次数均为1000，各算法在每个测试函数上均独立运行30次，测试环境保持一致，表2统计了维度为二维时各算法对不同函数寻优结果的平均值和方差。

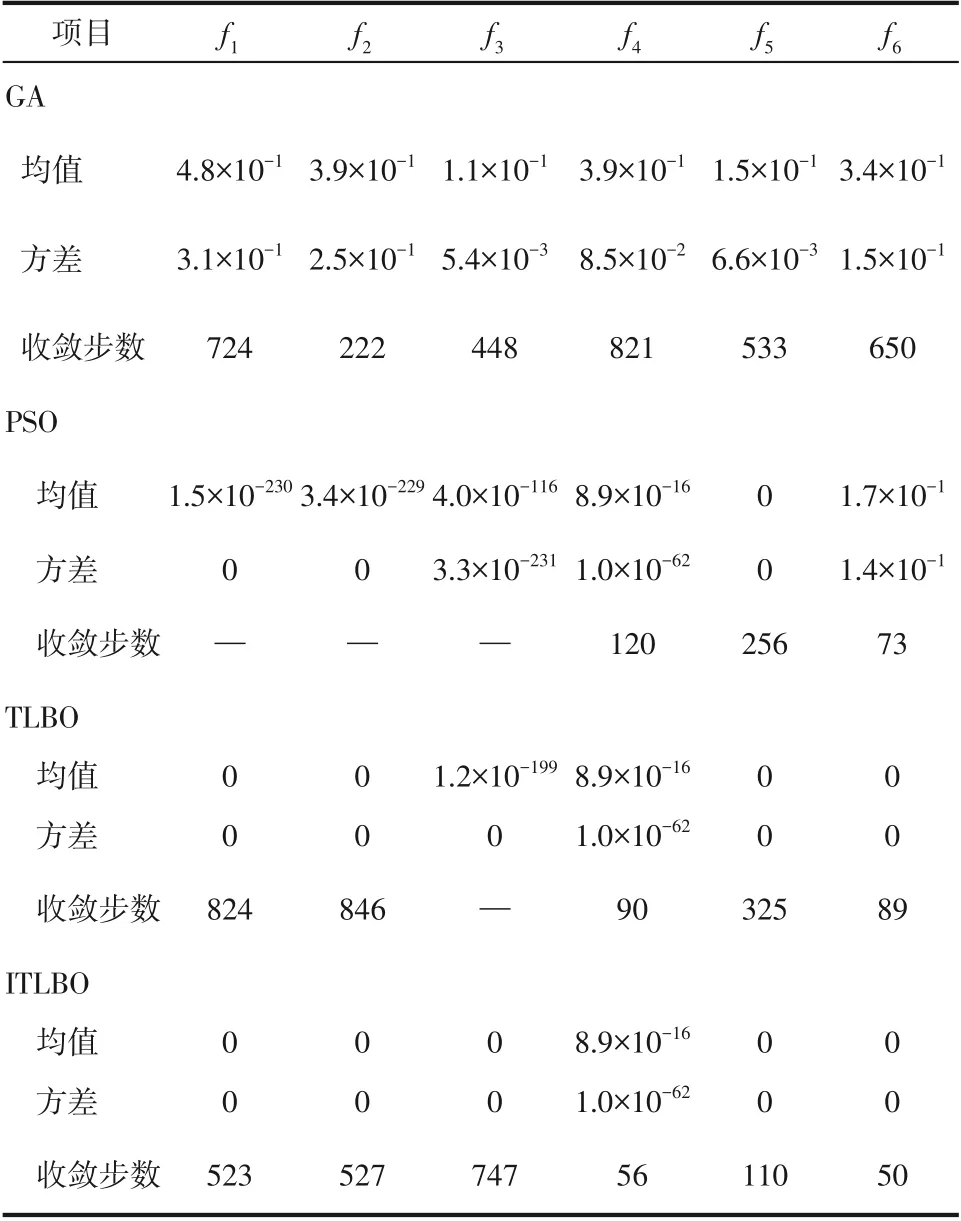
表2 benchmark函数测试结果

以函数为例，图8为4种不同算法优化时的收敛曲线图。当函数维度为二维时，从表2 和图8中可以看到，对于单峰函数和，TLBO 算法和ITLBO算法均可以找到全局最优解，但ITLBO算法的收敛速度更快，而GA 和PSO 算法在有限的迭代步数内没有找到全局最优解；对于单峰函数，只有ITLBO算法在有限的迭代步数内找到了全局最优解；对于多峰函数，GA、PSO、TLBO、ITLBO算法均没有找到全局最优解，但ITLBO算法的收敛速度最快；对于多峰函数，PSO、TLBO、ITLBO 算法均找到了全局最优解，但ITLBO算法的收敛速度最快；对于多峰函数，TLBO 和ITLBO 算法均可以找到全局最优解，但ITLBO 算法的收敛速度更快。

图8 f1函数的收敛曲线

计算结果显示，ITLBO算法始终能找到大部分单峰函数和多峰函数的全局最优值，寻优结果的精度和收敛速度均优于改进前的TLBO算法和其他算法，说明提出的ITLBO算法具有较好的鲁棒性和稳定性，算法的有效性得到了验证。

3 案例分析

3.1 支持向量机识别压降速率信号流程

支持向量机模型对压降速率信号分类的准确率受到内部惩罚系数和核函数参数取值的影响。因此，分别使用GA、PSO、TLBO 和ITLBO 算法求解这两个参数的最优值，并将分类结果进行对比。图9为支持向量机识别不同工况压降速率信号的过程，具体步骤如下：首先，为保证压降速率信号具有多样性，选取管道泄漏、压缩机抽吸和截断阀紧急截断工况下不同阀室的压降速率信号各200 组（共600 组）作为原始信号，这些信号均匀地覆盖了输量为(300～2100)×10m³/d、压力为5～10MPa、泄漏孔径为25～125mm、泄漏位置为两阀室间10%～70%的位置、压缩比为1.5～3.0 的边界条件。其次，由于采集到的压降速率信号维度较高，因此需要使用奇异值分解对压降速率信号进行特征提取。式(16)为特征提取过程中构建的轨迹矩阵的表达式，对其求解即可得到该条压降速率信号的特征信号。为了避免数量级的影响，还需对所有的特征信号进行归一化处理，归一化处理的表达式如式(17)。

图9 SVM识别压降速率信号过程

式中，,,…,x为各时刻对应的压降速率；为时间序列，即压降速率信号的长度，取60；为窗口长度，取10。

式中，为特征信号中的最小值；为特征信号中的最大值；为归一化的下限，取-1；为归一化的上限，取1。

然后均匀地将3类工况的特征信号各取70%作为训练集（共420组）进行分类器训练，剩余信号作为测试集（共180组）测试分类器的准确率，保证了训练集内的各类工况在测试集里都有与之对应的测试信号，使测试结果具有公平性。最后，使用优化算法优化支持向量机模型内的惩罚系数和核函数参数，得到识别不同工况压降速率信号的支持向量机模型后，将训练集输入模型中进行模型的训练，再使用测试集对模型的分类效果进行测试。

3.2 结果分析

按照上述步骤，对模型的分类效果进行测试。在寻优过程中，初始种群数量为30，迭代步数为80，和的寻优范围为[0.01,100]。支持向量机内其他参数固定，其中核函数类型为RBF 核函数，折交叉验证为5折，各算法优化的模型均独立运行30 次，取分类准确率的平均值作为结果，优化结果如表3所示。

由表3可知，ITLBO 算法优化的管道泄漏识别模型的准确率最高，整体平均分类准确率为98.5%，相比于TLBO算法提高了4.2%，且明显优于PSO和GA 算法。图10显示，ITLBO 算法优化模型的收敛步数为15，TLBO 为19，PSO 为46，GA 为58，说明ITLBO算法优化的模型较其他模型具有更快的收敛速度。应用结果与benchmark 函数测试结果一致，证明了ITLBO算法优化的泄漏信号识别模型较其他算法优化的模型在分类准确率和收敛速度上都有所提高。

表3 不同优化算法下模型的分类结果

图10 不同算法优化模型的收敛曲线

图11 为ITLBO 算法优化的管道泄漏信号识别模型的分类结果，图中纵坐标“1”代表泄漏工况、“0”代表压缩机抽吸工况、“-1”代表截断阀紧急截断工况，每种工况各有60 组测试信号。对于泄漏工况，测试信号的泄漏孔径为25～125mm，压降速率为0.001～0.1MPa/min，其中有1 组误识别为压缩机抽吸信号，准确率为98.3%；对于压缩机抽吸工况，测试信号的压缩比为1.5～3.0，压降速率为0.001～0.15MPa/min，其中有2 组误识别为泄漏工况，准确率为96.7%；对于截断阀紧急截断工况，测试信号的压降速率为0.02～0.1MPa/min，识别准确率为100%。

图11 ITLBO-SVM模型识别结果（相国寺储气库）

泄漏工况中识别错误的信号为50mm 泄漏孔径的信号，压降速率为0.01MPa/min；压缩机抽吸工况中识别错误的信号为压缩比1.5 时阀室的压降速率信号，压降速率分别为0.003MPa/min 和0.006MPa/min，分别对应泄漏孔径25mm 和50mm时的压降速率，这些信号的压降速率均小于0.01MPa/min。模拟了大量压降速率信号后发现，管段泄漏孔径小于50mm的上下游阀室、压缩机抽吸时距离压气站越远的阀室和距紧急截断的阀室越远的阀室，它们采集到的压降速率信号普遍小于0.01MPa/min，可能会出现个别信号识别不准确的情况。

如图12 所示，当压降速率小于0.01MPa/min时，压缩机抽吸工况和泄漏工况的压降速率信号在数值上和曲线特征上相近，进而导致模型分类失误。为此，针对50mm以下的小孔泄漏，建议通过气液联动阀与SCADA 系统数据监测的特征进行综合判断。例如，压缩机抽吸时的特征表现为各阀室的压降速率依次减小；管道泄漏时的特征表现为沿线某一个阀室的压降速率突然增大，其余阀室压降速率不变。根据这些特征可综合判断是否需要远程控制截断阀关断。

图12 压降速率信号对比

3.3 模型普适性验证

基于陕京三线实际运行数据，建立了榆林首站至临县压气站的仿真模型，管线全长181.1km，管径1016mm，沿线共有8 座阀室。同样模拟了泄漏工况、压缩机抽吸工况和截断阀紧急截断工况，所研究的输量为(2300～3450)×10m³/d、压力为7.5～8.8MPa、泄漏孔径为25～125mm、泄漏位置为两阀室间10%～70%的位置、压缩比为1.5～3.0。3 类工况各模拟了30 组压降速率信号，作为测试集对模型进行验证，见图13。

图13 ITLBO-SVM模型识别结果（陕京三线）

从图13 中可以看到，模型对于管道泄漏工况和截断阀紧急截断工况识别的准确率为100%；而对于压缩机抽吸工况，有1组信号被错误识别，识别的准确率为96.7%。该信号为压缩比为1.5 时远离压气站的某阀室的压降速率信号，压降速率为0.008MPa/min，被误识别为50mm 的泄漏工况压降速率信号，说明此时两种工况的压降速率信号近似。从模型整体的识别效果来看，90 组信号中仅有1 组信号识别错误，模型整体识别的准确率为98.9%，说明提出的模型能够适应不同属性的管道，模型具有一定的普适性。

4 结论

（1）提出的混沌映射和自适应惯性权重的教与学优化算法在种群初始化和平衡全局与局部最优能力方面得到提升。优化后的支持向量机模型对管道泄漏、压缩机抽吸、截断阀紧急截断工况识别的准确率为98.5%，较优化前提高了4.2%，模型具有一定的普适性。

（2）模型可识别当量直径为50～125mm的小孔泄漏，压降速率范围0.01～0.1MPa/min，识别准确率为100%。

（3）模型可识别的压缩机抽吸工况压降速率范围为0.001～0.15MPa/min，识别准确率为96.7%；可识别的截断阀紧急截断工况压降速率范围为0.02～0.1MPa/min，识别准确率为100%。

（4）当泄漏孔径小于50mm、压降速率小于0.01MPa/min 时，管道泄漏工况和压缩机抽吸工况的压降速率信号特征相似，导致模型对个别信号分类不准，此时建议通过气液联动阀与SCADA 系统监测数据综合判断管道是否泄漏。