航空发动机滑动局部线性模型及控制

蒋安常，韩永健，张伟，周振华，周龙，杨蓓

（1.中国航发贵州红林航空动力控制科技有限公司，贵阳 550000；2.南昌航空大学飞行器工程学院，南昌 330063）

0 引言

航空发动机是涉及工程热力与转子动力等多方面耦合的复杂非线性系统，其动态特性受工作状态和飞行条件的影响非常大，因此航空发动机的机理建模通常是1项非常艰巨的任务。现有的模型往往不具有非线性动力学的显式结构，通常可以用于航空发动机的性能分析，但并不利于控制器设计。因而，航空发动机的控制往往需要先获得1个具有显式结构的动力学模型，目前通常是在发动机飞行包线内的某些工作点上根据其运行状态对发动机非线性模型进行线性化处理，并根据线性化处理后获得的等效线性模型设计相应的适用于不同工作点的控制器，再根据工作点的变化，利用增益调度策略实现控制器之间的切换，从而保证航空发动机安全稳定运行。然而，这种控制方法存在着1个关键问题，就是某些增益调度策略对控制器通常是一种有扰切换，会造成发动机不平稳运行。如果切换频率较高，甚至可能导致严重的安全问题，对发动机的伤害较大。

为解决这一问题，杨蓓等提出了一种用多项式拟合在线构建发动机线性时变模型，并基于该模型引入了一种自适应神经网络控制方法来保证发动机控制过程的渐进收敛和稳定性。为了解决外界扰动、系统参数摄动和控制器切换扰动等问题，很多先进控制方法相继提出。王磊等提出了一种H∞容错控制；Ji等提出了一种基于线性矩阵不等式的H∞控制方法；张丽婷等、李彬等提出航空发动机模糊控制方法；罗隆等、郭迎清提出神经网络控制；Deepak提出预测控制；丁凯锋等、潘慕绚等提出自适应控制；任立通等、Divyesh等、刘金琨等提出滑模控制；苗卓广等、Sangwian、Dean等提出鲁棒多变量控制。在一定工作范围内，这些方法通常能够取得比较好的控制效果，但控制器通常比较复杂，很难保证控制系统在实际工作中的可靠性。由于工作点之间的距离较大，通过线性化处理后获得的等效线性模型存在着比较大的未建模动态，传统的鲁棒控制方法在实际工作中往往比较保守。所以，改进发动机模型是提高航空发动机控制系统设计的基本方法。

本文从提高航空发动机的控制性能和可靠性出发，研究了一种基于粒子群优化算法的航空发动机滑动局部线性建模方法。利用发动机工作过程中某一微小局部动态响应的在线数据来辨识一个给定结构的线性模型参数，从而获得某一工作点附近的线性模型。通过分析发动机燃油调节器的工作特性，建立了燃油调节器电液伺服阀和计量活门的传递函数，从而基于所构建的模型设计了一个航空发动机转子转速和燃油调节的双闭环自适应PI控制系统。

1 航空发动机控制结构

航空发动机双闭环控制系统结构如图1所示。其中内环是燃油控制回路，外环是转速控制回路。燃油系统主要由电液伺服阀、计量活门、等压差活门和执行元件等机构组成，通过改变电液伺服阀的控制电流来调节计量活门的输出，达到调节燃油流量的目的。

图1 航空发动机双闭环控制系统结构

燃油系统和航空发动机的动力学模型可以表示为

式中：为系统状态变量；为控制变量；(·)、(·)和(·)分别为表征系统内动态、控制增益和输出的函数。

燃油系统

航空发动机

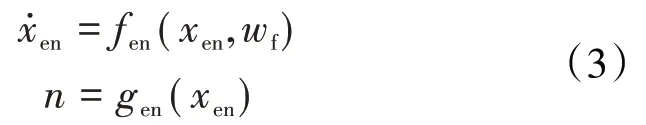
式中：为燃油系统的状态变量，也即计量活门阀芯位移；和分别为反映燃油系统内动态和控制增益的非线性函数；为电液伺服阀输入电流；为燃油系统输出矩阵；为发动机转子转速；为发动机状态变量；和为反映发动机动态和输出增益的非线性函数；为进入到航空发动机的燃油流量。

2 燃油系统模型

燃油调节器控制结构如图2所示。燃油计量执行机构采用了等压差活门辅助调节结构，其燃油计量活门位移通过闭环结构的电液伺服阀系统控制。

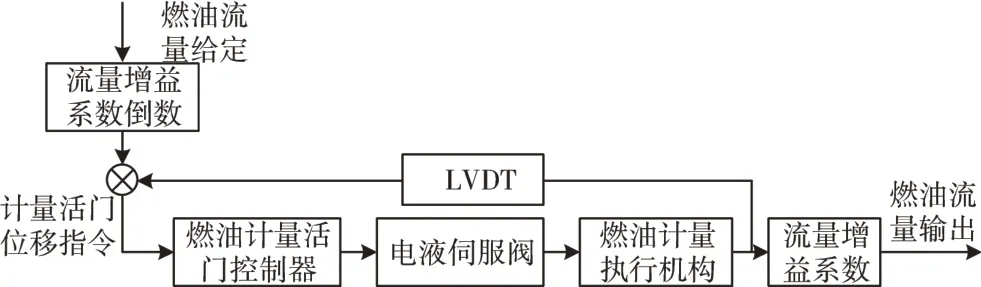
图2 燃油调节器控制结构

电液伺服阀模型的传递函数为

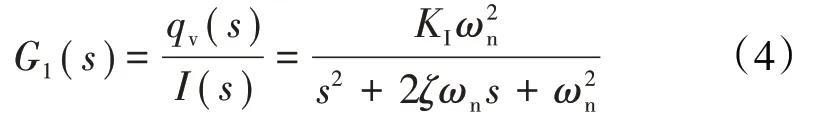
式中：()为电液伺服阀流量；()为输入电流；为稳态增益，其值为最大流量对应的输入电流之比，即=；和分别为电液伺服阀的固有频率和阻尼比。

对某型电液伺服阀非线性模型特性线性化处理，得

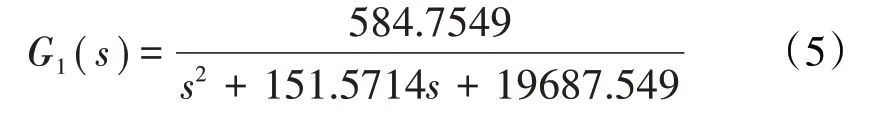
通过电液伺服阀流量()改变计量活门左右控制腔压力，来改变计量活门阀芯位移()。通过分析计量活门内部流量和压力平衡关系，可以建立其电液伺服阀流量与计量活门阀芯位移之间的传递函数

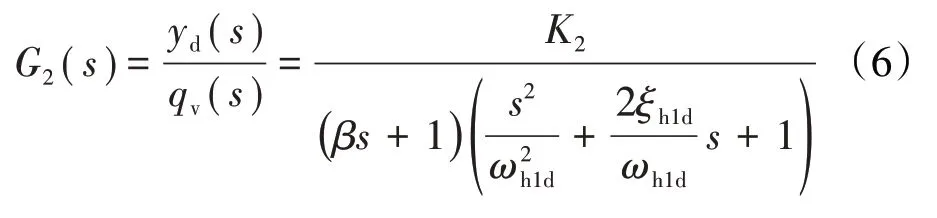
式中：为阀控非对称活门系统活塞杆伸出时的液压固有频率；为阀控非对称活门系统活塞杆伸出时的液压阻尼比；和分别为与弹簧弹性系数、计量活门流量压力系数和计量活门有效面积有关的系统参数。

一般情况下，远大于1，因此计量活门在低频段呈现出积分特性，也即传递函数（式（6））可近似为

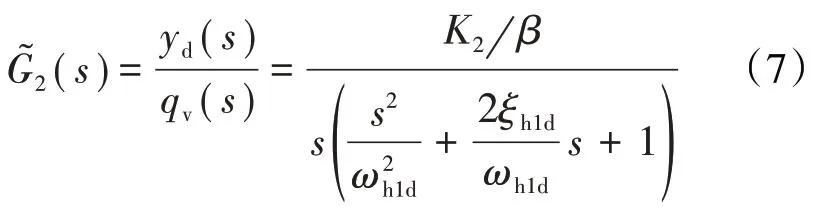
对于某型燃油调节器，把结构参数代入式（6），可得计量活门的传递函数

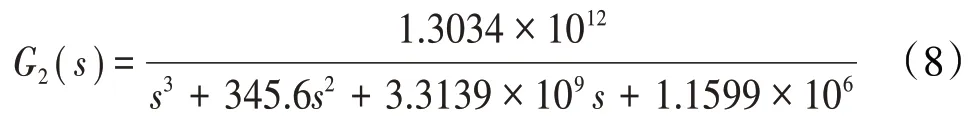
而由式（7）得其近似形式为

近似处理前后计量活门传递函数的频率特性如图3所示。传递函数（式（9））除了有1个在原点的极点，还存在1对共轭极点（-171.05±57567）。由于这对共轭极点远离虚轴，因此在低频段，即在频率为0.01～60000 rad/s内，这对共轭极点对计量活门频率特性的影响非常小，所以式（9）可进一步简化为

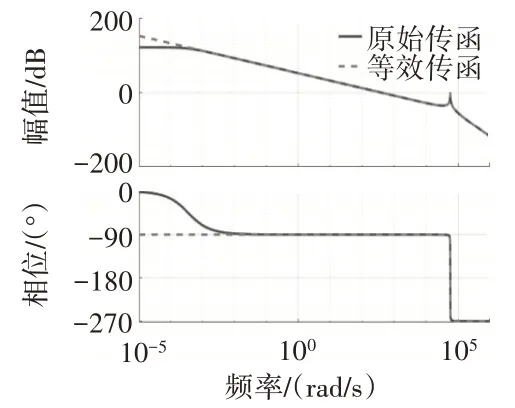
图3 近似处理前后计量活门传递函数的频率特性

那么燃油调节器传递函数为

上述燃油调节器传递函数中的2阶环节属高频动态可忽略，近似处理为

燃油调节器传递函数近似处理前后的频率特性如图4所示。输入电流为30 mA时燃油系统降阶处理的计量活门阀芯位移时间响应对比结果如图5所示。从图4、5中可见，在低频段燃油系统等效传递函数能够很好地逼近燃油系统的动态。

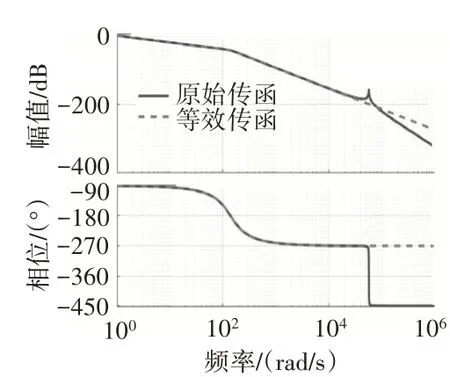
图4 燃油调节器传递函数近似处理前后的频率特性

图5 输入电流为30 mA时燃油系统降阶处理的计量活门阀芯位移时间响应对比结果

由于电液伺服阀与计量活门构成的系统本身含有1个积分环节，按照燃油超调量小于5%性能指标设计，可采用比例控制方式，比例系数可选为10，燃油闭环PI控制时间响应如图6所示。

图6 燃油闭环PI控制时间响应

燃油计量执行机构的闭环传递函数为

由于该型燃油调节器工作频率在2000 Hz以下，所以燃油流量闭环传递函数可简化为

燃油调节器闭环频率特性如图7所示。

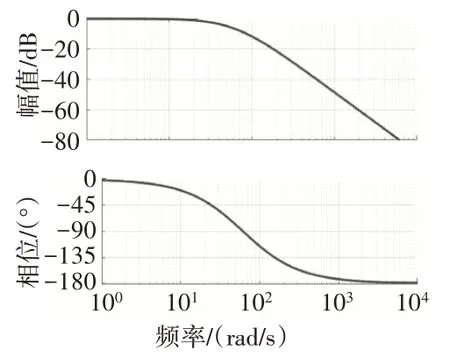
图7 燃油调节器闭环频率特性

3 发动机滑动局部线性模型

航空发动机非线性动态特性在1个局部小范围内可以用1个线性模型来逼近，如果这个小范围随发动机工作状态不断滑动，则可建立发动机自适应线性模型。

3.1 滑动局部线性模型辨识方法

发动机系统的输出是可检测的，则设定控制步长（即采样周期）为。那么线性模型能够精确逼近发动机非线性动态的局部区域范围就可以用这个区域的控制步数来表征，考虑转子转速作为1个状态变量，发动机局部线性模型为

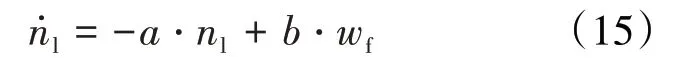
式中：和分别为模型的未知参数。

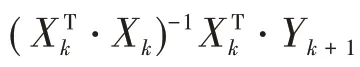
由于这个最优化问题并不是典型的凸优化问题，所以传统的非线性规划方法如有效集法和内点法等通常很难取得比较好的效果，而且优化性能往往也取决于模型参数初始值的选择。从提高局部线性模型性能和整个发动机控制性能角度来说，在求解上述模型参数优化问题时必须尽可能寻找到全局最优解。针对非凸优化问题，以遗传算法和粒子群算法为代表的进化优化方法通常能够取得更好的优化结果。

局部优化模型参数的粒子群算法步骤如下：

step1：初始化粒子群算法参数，包括最大迭代数，种群规模；

step2：产生初始种群=[,…,θ]，每组模型参数可看作是1个粒子；

step3：for=1：；

step6：获得当前种群的适应度=∪Fend；

step7：获得当前种群的最优适应度值和最优粒子

step8：for=1：G；

step9：利用当前种群的最优适应度值和最优粒子来更新种群所有粒子位置和速度，从而产生子代粒子种群；

step10：重复step4～step6的步骤计算更新后每个粒子的适应度值；

step11：更新种群粒子历史最优位置和速度；

step12：更新种群的最优适应度值和最优粒子end；

step13：输出最优模型参数。

滑动局部线性模型辨识还需要考虑另外2个问题：局部区域的大小，也即辨识区间大小问题；模型辨识的频率问题。由于发动机模型是强非线性系统，如果设定的局区域太大，那么线性模型将会出现很大的模拟误差，线性模型在不同辨识区间的性能如图8所示。

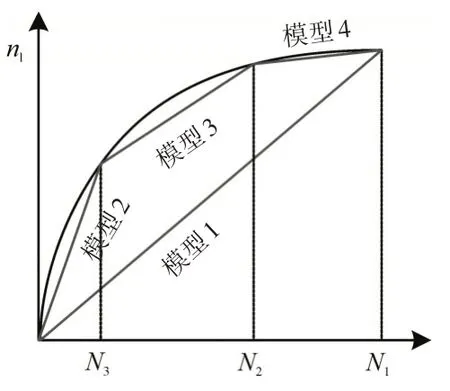
图8 线性模型在不同辨识区间的性能

从图中可见，对于1个给定的非线性函数，如果辨识区间选为，那么模型1产生的模拟误差很大，但如果把区间再细分成3个更小的区间，并用3个小区间的线性模型来逼近非线性函数，则模拟误差要比大区间线性模型的小很多。所以辨识区间的选择对滑动局部线性模型来说非常重要。理论上辨识区间越小，则辨识误差就越小；但减小辨识区间，发动机线性模型的辨识频率就会提高，给发动机计算机控制系统带来很大的计算负担，难以保证发动机控制的实时性。所以需要合理选择辨识区间。一般来说，如果模型的辨识时间为，那么滑动局部线性模型的辨识频率应当不大于2，也即辨识周期应当不小于0.5。局部滑动线性模型的更新过程如图9所示。

图9 局部滑动线性模型的更新过程

从图中可见，0为模型1的辨识区域，而为模型1的作用域。如果把模型1的作用域扩展到，那么模型的误差会相当大；但如果在时刻利用新的采样数据来更新模型，那么模型的模拟误差将会大大减小，如模型2在之间的模拟误差远小于模型1的。当考虑模型辨识时间时，辨识周期-要不小于0.5。

3.2 滑动局部模型性能验证

在零高度、零马赫数的测试条件下，某型航空发动机燃油流量和转子转速测试结果如图10所示。采样周期为0.01 s。

图10 某型航空发动机燃油流量和转子转速测试结果

为了验证不同辨识区间大小对逼近误差的影响，在仿真试验中考虑了20种不同区间，也即分别取连续采样点数=10,60,110,…960。粒子群算法的种群规模设置为100，最大迭代数设置为100，不同辨识区间的模型累积误差和辨识时间如图11所示。从图11（a）中可见，当＜500时滑动局部线性模型的累积误差都非常小；但当≥500时，模型的累积误差急剧增大，这意味着当辨识区间过大时线性模型已经不能反映发动机的真实动态过程。从图11（b）中可见，不同大小的辨识区间参数辨识所用的时间相差不大，其均值为0.8698 s，只是有时辨识时间会较长，这主要是由粒子群优化的随机搜索特性引起的，也就是当初始随机种群远离最优解时搜索速度较慢，搜索时间也就延长；反之，如果初始种群刚好在最优解附近，那么搜索速度很快，搜索时间也就缩短。从结果来看，对于该型发动机，滑动局部线性模型辨识的辨识区间≤400，而线性模型的更新周期应当小于2 s。

图11 不同辨识区间的模型累积误差和辨识时间

对该型发动机在400 s内的运行，取=200，在模型更新周期为1 s的条件下，滑动局部线性模型的模拟结果如图12所示。从图12（a）中可见，在大多数情况下利用滑动局部线性模型能够很好地逼近发动机的真实动态，但在某些时刻仍会出现较大的模拟误差。其原因是粒子群算法是一种随机优化算法，不总是能够搜索到全局最优解，有时会出现种群早熟的情况。这时优化过程就容易陷入到局部最优，所以粒子群算法存在一定的失效概率。

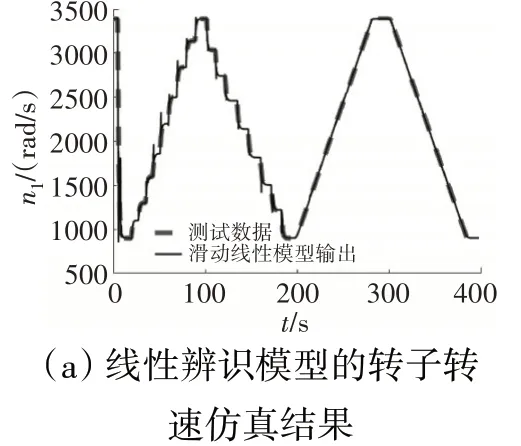
图12 局部滑动线性模型的模拟结果

从图12（b）、（c）中可见，线性模型在滑动过程中2个模型参数变化有时比较剧烈，这通常是因为粒子群算法陷入到局部最优而导致的。在发动机非线性比较强的地方由于逼近误差较大，粒子群算法在有限迭代次数下可能无法收敛到全局最优，从而导致较大的模型误差。针对这种情况，在控制过程中通常需要设计具有一定鲁棒性的控制器来减小模型误差对控制性能的影响。

4 基于滑动局部线性模型的燃油与发动机状态反馈控制

对于某一辨识区间，假定所获得滑动线性模型的2个最佳模型参数分别为和，那么发动机转子转速动态就可以用如下线性模型来逼近

其传递函数为

考虑燃油系统闭环传递函数，得到整个航空发动机控制系统的开环传递函数为

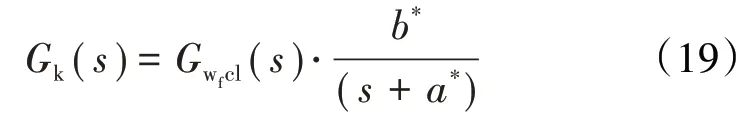
式（11）所示的燃油子系统闭环传递函数可采用PI控制器，其传递函数为

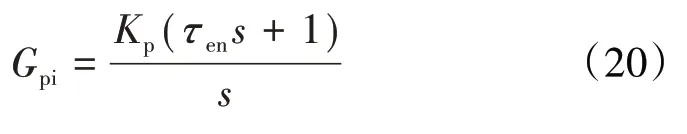
式中：为PI控制器放大倍数；为积分参数，选取=1，那么校正后的燃油与发动机系统的开环传递函数为

当系统工作频率小于100 rad/s时燃油闭环系统将退化为1个惯性环节，即燃油闭环系统等效为

燃油闭环系统近似处理前后的频率特性如图13所示。

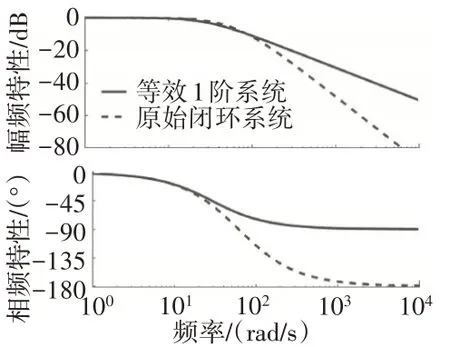
图13 燃油闭环系统近似处理前后的频率特性

这样，校正后的燃油与发动机系统开环传递函数为

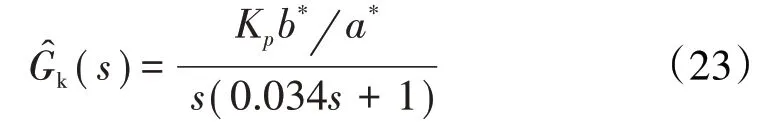
那么有=。可见转速控制器的参数随滑动局部线性模型的辨识参数变化，相当于PI控制器具有自适应能力。因此这种基于滑动局部线性模型的燃油与发动机双闭环控制可以看作是一类特殊的自适应控制方法。本次仿真试验以图10（a）中的实测转子转速作为参考转速，则基于滑动局部线性模型的PI双闭环控制结果如图14所示。

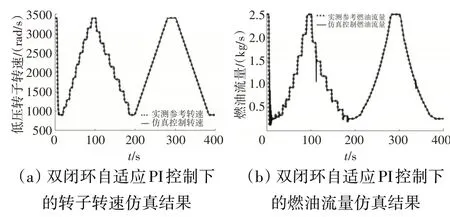
图14 基于滑动局部线性模型的PI双闭环控制结果

从图中可见，这种双闭环PI控制能够取得比较好的控制效果，转子转速在大多数情况下能够精确地跟随参考转速的变化，特别是在小阶跃参考输入和斜坡参考输入下，跟踪效果非常好。但在大阶跃阶段，也即运行5～10 s阶段，转速接近900 rad/s时出现一定的振荡。主要原因是在大阶跃阶段滑动局部线性模型对发动机真实动态的逼近存在较大误差，特别是当辨识区间L较大时这种情况更为突出。辨识频率过高甚至会引起发动机控制信号的失步，有些控制信号不能及时传送到执行机构中，给飞行器的飞行安全带来很大威胁。如何来平衡滑动局部线性模型的辨识频率和控制性能是非常值得研究的重要问题。此外，综合考虑限制保护控制等因素，这种大阶跃也可以由斜坡信号代替，以改善系统的控制性能。

5 结论

（1）电液伺服阀和燃油系统中的高频动态对发动机转子转速的性能影响较小，在控制系统设计时可忽略。

（2）通过滑动局部线性模型可描述发动机非线性动态。滑动辨识区间大小对线性模型的模拟性能和对发动机的控制性能影响较大，在选择辨识区间大小时需要考虑可能的大累积误差，并应合理选择辨识频率以确保控制系统的实时性。

（3）粒子群算法由于其随机搜索特性，有时会陷入局部最优搜索和种群早熟，造成滑动局部线性模型模拟性能降低，导致自适应控制性能降低。如何避免粒子群算法陷入局部最优搜索，有必要在后续工作中进一步研究。