可视化系统预测技术研究

高泽文 解中洋 任俊达 马宁

湖南师范大学 湖南 长沙 410000

1 可视化技术概述

1.1 ArcGIS Dashboard技术概述

ArcGIS Dashboard是以地理空间数据为核心，将各种地理信息以专题图表等诸多面板展示的一套应用Web服务资源的终端展示平台。系统可以通过诸多类型操作面板来表现，包括业务信息列表、专题统计图表、指标监控仪表，外部内容等，同时支持副文本。基于空间位置资源应用的地图面板是其核心内容，将以上诸多资源面板和地理空间信息结合应用，能够最大限度地发挥业务信息价值。ArcGIS Dashboard数据源主要是以Web Map形式进行数据接入展示的，所以必须将表格等数据放入Web Map中，同时对要展示的分省级，市级，县级以及确诊小区等数据进行地图配色等，最后保存Web Map。数据更新可以利用ArcGIS API For Python或其他ArcGIS API完成数据的实时更新。ArcGIS API For Python能够通过Python灵活快速构建地理空间要素的Spatial Data Frame，从而更新源数据的Spatial Data Frame，完成Feature Service的实时更新。

1.2 ArcGIS Dashboard参数配置

为了更快地完成可视化系统软件构建，软件架构设计基于ArcGIS Dashboard技术。可视化系统架构包括：

1.2.1 数据层。将数据存储在常使用的关系式sqlserver 或oracle 中的数据库[]。部分文本文档形式的数据可以使用csv或xls的方式存储在excel表格中，简单的室内空间数据可以存储在几个压缩为zip包的shp格式文件中。

1.2.2 服务项图层。通过ArcGISServer将数据图层的数据发布为ArcGIS Rest服务项或其他通用OGC服务项。如果室内空间数据量较小或变化不大，可以不发布服务项目，可以立即发布服务项目。通过文档与主要表示层进行交互通信。同时，将必须查看的检验数据作为矢量材料要素服务项目发布，方便查看。对于经常查看的功能，比如年月量指标等数据，可以根据前期设计方案的数据库结构编写相应的预统计分析服务项目，在后台管理中完成预计算，并加快之前数据呈现的速度。

1.2.3 主表示层。以地图为主，将信息可视化。服务项目层的地理信息服务项目用于显示地图，并配备相应的样式，使地图因素在网络镜像中具有唯一性。借助车内仪表盘的设计理念，加强了UI上各个因素之间的交互，通过目录、仪表盘、指标等多种手段表达了关键指标值。据客服平台介绍，主表现层配备响应式UI，使其更能兼容电脑浏览器的尺寸。

2 预测技术

2.1 相关性评价指标

本文主要选取的是Pearson相关系数和speraman相关系数，这两个指标分别描述了两个数据组合的线性相关性和测量变量之间的相关性水平。

2.1.1 Pearson相关系数。皮尔森相关系数（Pearson Correlation Coefficient）用来考虑两个数据的组合是否在一条线上，用来考虑间隔变量之间的线性相关。计算公式为：

皮尔森相关系数的值用上述公式来表示，COV是2个变量的协方差，真分是2个变量的标准差的乘积。μx是X的平均值，μY是Y的平均值，E为期望。

皮尔森相关系数是线性关系的一个指标，它反映了两个量之间线性关系的高低。这个值常用小写字母r来表示。r值范围在-1到1之间，绝对值越接近于1，相关性越强（负相关/正相关）。

2.1.2 speraman相关系数。以查尔斯·爱德华·斯皮尔曼命名的斯皮尔曼等级相关系数，即斯皮尔曼相关系数[]。它是一个考虑两个变量相关性的非主参数索引值。它使用简单的方程来评估两个统计分析变量的关联[3]。如果数据中没有重复值，并且当2个变量完全简单相关时，Spearman相关系数为1或-1。对于有n个样本的模板，将n个初始数据转化为水平数据，相关系数ρ为：

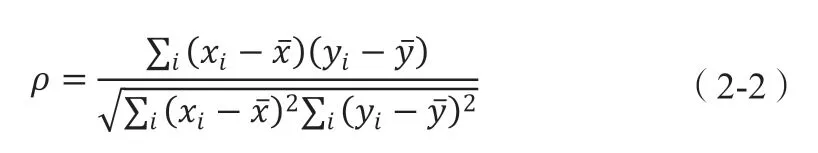
speraman相关系数也可以称为“秩相关”；换句话说，观察数据的“排名”被“排名”所取代。在连续除法中，观测数据的秩通常总是低于秩的一半。众所周知，在这个例子中，秩和秩相关系数是相同的。更一般地，观察数据的“等级”与可能的整体模板的比率低于给定的值，即观察值的一半。也就是说，是对应等级指标的一种可能的解决方案。尽管不常见，但仍可能使用“级别相关”。

二者的区别在于：①分析范围不同：Pearson用于计算连续数据的相关，而speraman相关是专门用于分析顺序数据，二者分析范围不同。②用途不同：Pearson相关是最常见的相关公式，用于计算连续数据的相关性。而spearman相关是专门用于分析顺序数据的，就是那种只有顺序关系，但并非等距的数据。

2.2 数据来源

本文的所研究的数据源包括好搜指数和媒体网站颁布的信息。

无论是百度指数、好搜指数，还是淘宝指数等等，都是围绕一个重点：关键词。也可以统称其为：关键词搜索指数。指数越高，代表关键词越热门，搜索的人就越高。

好搜指数，它是一个基于大量网民个人行为数据的数据共享平台。它是当今网络乃至整个数据周期中最重要的数据分析服务平台之一。好搜指数值主要包括：科研发展趋势、对top的要求、舆情管家、人群特征。通过分析，本人确定的好搜指数关键词包括：X1，“病毒”（X2），“预防”（X3），“症状”（X4），“核酸检测”（X5）[]，“传染”（X 6），“季节”（X7）和“疫苗”（X8）。

2.3 数据和搜索指数相关性分析

定义式（2-1）中的X为好搜热点指数，Y为某地区的患病人数（或死亡，治愈人数等），计算在一段时间之内的皮尔森相关系数，看好搜索指数的值与总数之间是否存在线性关系和依赖关系。

2.4 基于回归模型的预测分析

根据总数据与好搜指数值的相关性分析，当前数据与好搜指数值中部分关键词的检索频率具有线性相关和依赖感[]。因此，分析和预测是在构建多元线性回归线性模型的基础上进行的。

假设患病人数（或死亡、治愈人数等）Y 与多个好搜指数X1,X2,..,Xn呈现强相关的关系，而此时我们认为，当这些X变量发生变化时，相应的Y也会随之发生变化。通过历史数据，我们可以得出Y与各变量X之间的某种关系，即：

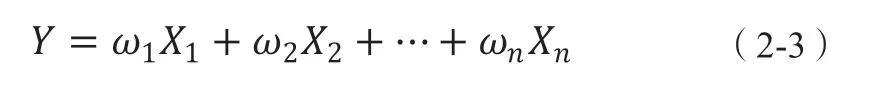
这样，就建立了Y与X之间的多元线性回归模型。此时，当人数数据无法实时获得，或者出现统计误差时，我们就可以根据式（2-3）对Y进行预测，而此时我们需要建立的工作就是获取各变量X的数值。

下面进行详细的建模步骤说明。

在统计分析中，多元线性回归优化算法是一种非常适合的优化算法，其应用非常普遍[]。多元线性回归概念：关键是在因变量和几个自变量之间建立线性相关性。这里的自变量一般是两个或两个以上。根据一系列计算得到的多元线性回归方程为多元线性回归实体模型。

多元线性回归数学分析模型如下：

因变量设置为y，自变量设置为x1，x2，...，xn-1，共有m组观测数据。存在如下所示的线性相关性：

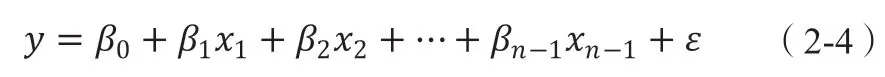
获得 m 个单独观察的 m 组数据样本：

其中，所有误差项都是相互独立的，且服从均值为0的正态分布。

此时，令：

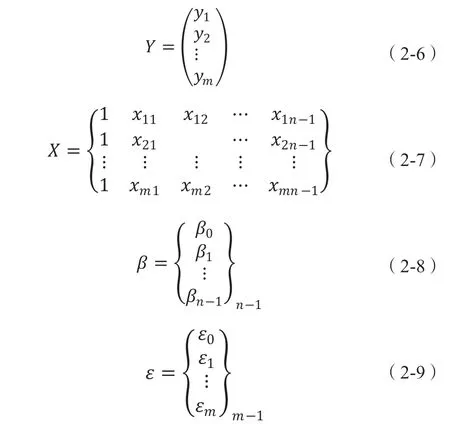
那么，公式计算（2-4）可表示为：

确定多元线性回归模型后，主要参数必须可能未知。所选择的方法通常是一般最小二乘法。设分别是参数的最小二乘估计，那么y的观测值可以表示为：

其中，k=1,2，…，N0；ek是误差的估计值。

根据最小二乘法，观测值和回归值之间的误差的均值Q应该最小，并且指定的Q越低越好。Q 是偏差的总数。

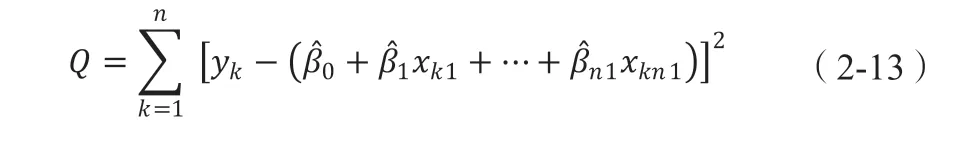
让公式计算（2-13）有一个最小值，根据极值点的基本原理可以计算得到满足条件的最小值。最后，通过求解矩阵方程得到相关系数的最小二乘法可能为：

为了保证模型的质量和系统设计的适当结果，重要的是对收集的初始数据进行数据转换和解析，以去除维度并使其具有可比性。

前文对回归分析模型进行了建模流程的介绍，下面还需要对数据的处理进行说明。由于此次回归模型中的变量，不仅涉及人数等简单的数字变量，还涉及搜索指数、热点等其他不易度量的变量，这些变量的量纲和取值方式也不同。因此，需要采取一定的数据变换技术。

为了保证建模的质量和系统分析的正确结果，必须对采集的原始数据进行数据信息转换和解析，去除维度，使其具有可比性。