基于线性数据重构的天线动力学模型辨识方法*

侯晓拯 许 谦 李 琳 易乐天 薛 飞 王 惠 许多祥 何飞龙

(1 中国科学院新疆天文台乌鲁木齐830011)

(2 中国科学院射电天文重点实验室乌鲁木齐830011)

(3 新疆射电天体物理实验室乌鲁木齐830011)

(4 新疆大学物理科学与技术学院乌鲁木齐830046)

(5 中国科学院大学北京100049)

1 引言

射电望远镜天线的俯仰、方位传动链, 作为望远镜伺服控制系统的主要被控对象, 常利用天线开环条件下的激励与响应采样数据进行参数辨识与建模. 传统系统辨识方法有最小二乘估计、Kalman观测器辨识法、Hankel子空间法、N4SID(Numerical Subspace State Space System Identification)法等[1–4],此类方法受限于线性假设,但辨识原理简单, 通过辨识模型可以进一步求解系统的各类稳定性判定参数与控制参数, 在辨识低阶线性模型时使用广泛. 而针对非线性模型, 以上方法辨识阶次较高. 近年来随着神经网络技术的迅速发展,利用神经网络可以任意拟合各类线性、非线性的函数特性, 常见的如: 自回归神经网络、径向基神经网络、支持向量机等[5–6]也被用于控制系统的建模. 此类方法虽然建模精度高, 但随着网络节点数增加训练计算量随之变大, 使用时需要较高的硬件成本, 如用于大口径射电望远镜天线的运动预测,则计算时间超出了控制器运行的最大指令间隔. 首先, 射电望远镜在实际建模过程中, 由于望远镜服役现场的工况较为复杂, 采样数据常受到各类环境噪声或采样设备内部扰动的影响. 其次, 辨识工作还受到采样设备性能限制, 如采样频率不足导致的高频采样噪声, 混叠、量程不足导致的采样饱和等[7]. 针对这些噪声与影响, 常使用各类滤波器, 降低采样数据的高频噪声[8–9]. 最后, 摩擦与回差等非线性特性也会导致采样出现畸变, 致使采样数据中出现高频分量[10], 增加了模型辨识难度. 为降低非线性特性影响, 需要测量非线性特性并补偿, 这也增加了系统辨识的工作量[11–12]. 若通过更高的模型阶次或更多的神经网络节点数直接拟合系统特性, 又会增加模型的辨识难度与计算时间, 降低模型适用性.

数据重构的方法多用于传感器采样, 机械臂插值等领域, 可在损失少量采样数据原始特性的前提下尽可能消除噪声与扰动的影响[13–15]. 本研究采用这一思路, 通过数据重构, 降低天线传动链建模采样中非线性特性对被控对象的影响.

本研究首先分析伺服控制系统非线性特性受到系统开环正弦激励信号后的畸变及各类扰动来源[16–17]. 之后, 计算系统响应矩阵的Hankel矩阵奇异值, 预估系统辨识复杂度[18]. 最后, 利用线性数据重构法, 降低系统辨识难度. 通过构建受到典型非线性摩擦力与迟滞影响的半实物实验平台, 模拟天线特性, 以平台实际采样数据为基础, 利用数据重构法, 降低非线性特性对模型辨识的负面影响,建立仅包含少量节点的自回归神经网络模型, 验证线性数据重构方法的有效性.

2 非线性特性影响

射电望远镜天线伺服控制系统从内到外通常分为力矩环、速度环与位置环, 内外环之间为积分关系. 以天线传动链中常见的摩擦死区与迟滞环为例, 这两种非线性特性常见于负载轴与轴承、减速机齿轮间. 若传动链中有使用螺栓进行连接与紧固, 则螺栓也可以等价为摩擦与间隙的结合. 图1中实线为正弦信号经过死区与迟滞环节并积分后的波形, 虚线为线性波形. 通过对比可知, 信号受到非线性影响后, 出现了波形畸变, 幅值下降, 且波形斜率出现变化, 为信号带来其他频率的分量.

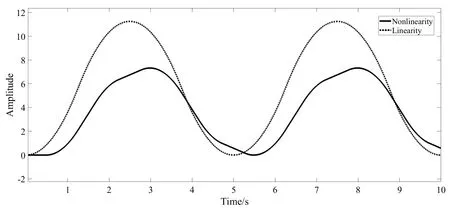
图1 多种非线性特性Fig.1 Multiple nonlinear characteristics

为辨识系统模型, 常利用正弦扫频信号作为激励, 激发系统特性. 理想线性系统受迫振动的稳定响应与激励信号频率相同, 若系统受到非线性特性影响, 根据非线性系统的受迫振动特性: (1)非线性受迫振动的响应为激励频率和次频率的组合频率;(2)幅值对应频率的响应出现跳跃现象, 可得出推论, 非线性系统激励响应的幅频关系将不再一一对应, 低频响应将叠加高频分量. 而此类分量, 并不源自系统外部扰动, 不应作为噪声被滤除, 而应当作为动力学特性保留. 因此, 非线性特性不仅会影响天线伺服控制系统性能、降低系统精度、延长调节时间, 在对系统进行动力学模型辨识时, 若辨识方法基于开环激励与响应数据, 非线性特性对系统的辨识同样具有负面影响. 根据模型辨识方法不同, 非线性特性会提高模型的辨识阶次或网络节点数量, 增加模型辨识难度. 系统辨识模型的阶次, 可通过计算系统激励响应信号的Hankel矩阵奇异值预先评估. 计算公式如下:

其中矩阵A为通过系统响应序列重构的Hankel矩阵, 每一条逆对角线上的元素都相等,U和V均为单位正交阵,Σ矩阵仅在主对角线上有非零值, 即为系统激励响应奇异值. 可根据奇异值拐点, 预估模型阶次[18].

若要降低采样信号中的高频分量, 需要测量系统中导致高频分量的非线性特性并补偿, 这将会较大地增加系统建模工作量. 与无人机、倒立摆等强非线性系统不同, 射电望远镜天线传动链中的非线性特性来源主要为轴承、齿轮间的摩擦力死区、大惯量与负载形变导致的少量迟滞环节, 在系统特性中不占主导地位. 因此, 可采用线性数据重构的方式, 损失少量系统模型精度, 削弱非线性影响.

3 数据重构

数据重构是根据已有少量原始采样数据, 通过插值、拟合等方法, 增加可用数据的过程. 非线性特性会使模型阶次的增加, 主要是由于改变了系统响应曲线的斜率. 非线性数据的线性重构, 即根据非线性系统响应信号的幅值、相位,重构线性信号.

信号的幅值可通过取包络的方式获得. 包络线是与目标曲线的每个顶点都有至少一点相切的曲线.

假设离散曲线为f(x,t), 则通过联立以下的方程, 可求得曲线的包络:

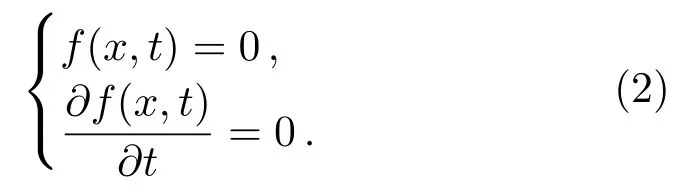
x为曲线某点的值,t为采样时间. 然后构造采样频率与实际激励信号一致的单位正弦信号. 重构正弦信号与实际采样信号会存在相位差, 相位差可通过补零对齐. 最后, 将重构正弦信号与包络值逐点相乘, 获得与原系统响应具有相同幅值、相位的线性重构信号. 利用重构的线性数据, 可以通过较低的阶次或较少的神经网络节点辨识系统模型.

4 验证实验

通过搭建半实物实验平台, 模拟天线俯仰轴特性, 验证线性重构法的有效性, 该平台受典型摩擦死区与迟滞影响. 如图2所示, 平台由伺服电机、81倍减速机、螺栓螺母紧固连接的桁架负载及安装在负载一端的陀螺仪构成. 电机转速为0–1000 rpm, 可通过激励信号控制电机转速带动负载旋转. 陀螺仪可测量负载一端的角速度, 量程±2000° ·s-1. 激励信号为0–25 Hz的正弦扫频信号,幅值为±1000 rpm, 陀螺仪采样频率为200 Hz.

图2 半实物实验平台Fig.2 Semi-physical experiment platform

在电机驱动器输入正弦扫频激励信号后, 利用陀螺仪测得的负载末端响应曲线, 如图3所示. 由于扫频信号的频率最大值为0–25 Hz, 为抑制噪声,利用零相位滤波器低通滤除25 Hz以上信号. 蓝色曲线为滤波信号, 红色曲线为原响应采样信号. 由于系统采样频率为200 Hz, 通过图3的采样数据估算可得, 响应信号在10 Hz与16 Hz左右的谐振点处,采样信号有大量的高频分量被滤除, 谐振点处的动力学特性受到了极大的削弱.

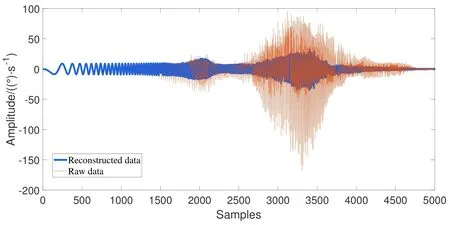
图3 原始采样数据与滤波后数据的系统扫频响应对比Fig.3 System sweep response comparison of original sampling data and filtered data

谐振点处的响应信号与非谐振区间相比, 噪声频率与对应的扫频信号不同, 为低频信号与高频信号的叠加. 非谐振区间并无与幅值等比的高频噪声出现, 噪声主要集中在谐振点处, 排除外部扰动的可能.陀螺仪采样频率200 Hz远大于激励信号上限,满足香农采样定律, 因此排除共振频段的高频噪声为欠采样高频混叠的可能. 根据非线性系统受迫振动特性, 可以确认该噪声为非线性特性对系统响应的畸变, 应当被保留, 不应被滤除.

根据系统扫频响应信号, 绘制原始采样信号与重构信号的伯德图, 图4是伯德图中的幅值部分, 其中蓝色是原始采样信号, 红色是重构信号. 然后, 计算响应信号前100阶的奇异值, 采样信号与重构信号前100阶奇异值对比结果如图5所示, 图中蓝色是原始采样信号, 红色是重构信号, 纵坐标为奇异值.由伯德图的幅值部分与奇异值分布图可知, 系统中因非线性特性的影响, 响应信号存在大量的高频分量, 10 Hz与16 Hz处的谐振幅值被高频分量明显削弱, 且前100阶奇异值未见明显拐点. 因此, 若根据此采样信号直接辨识模型, 则需要较高阶次的函数或较多的神经网络节点以拟合高频特性, 且模型中前两阶的谐振特性将与实际系统出现较大的差异.

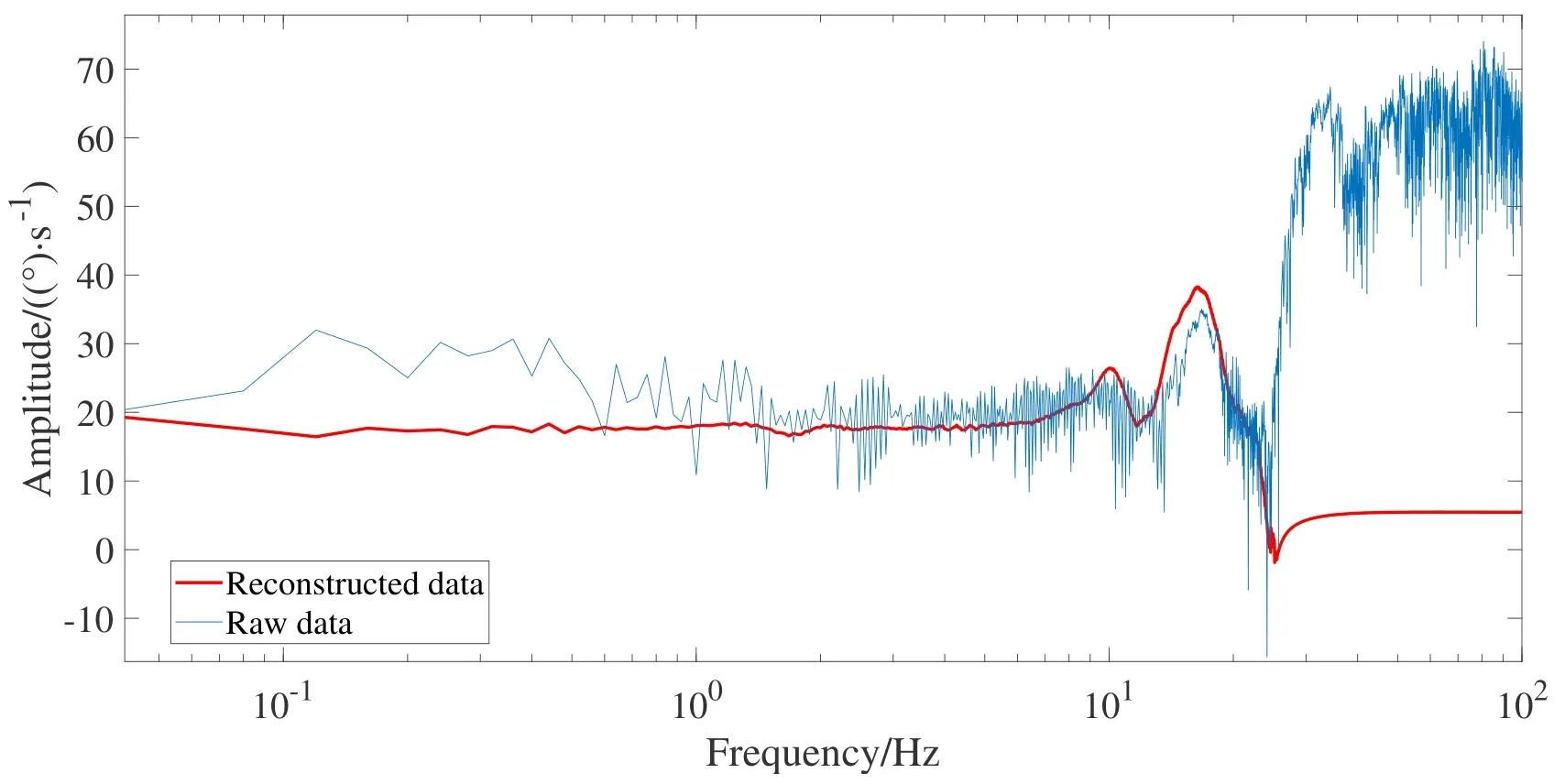
图4 采样信号与重构信号伯德图幅值部分Fig.4 Bode plot amplitude part of sampled signal and reconstructed signal

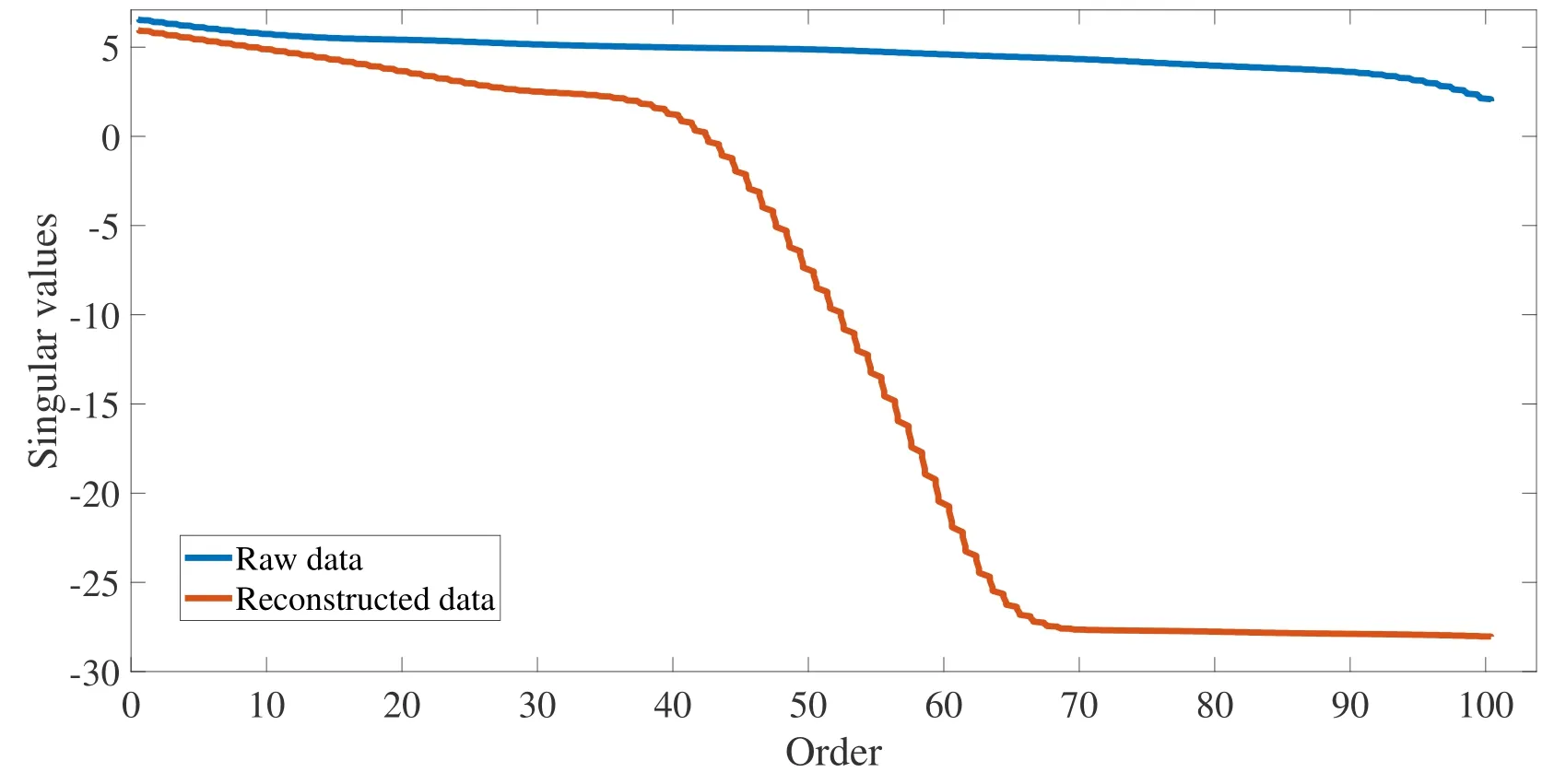
图5 采样信号与重构信号前100阶奇异值Fig.5 The first 100 orders singular values of the sampled signal and the reconstructed signal

以系统实际响应为基础重构线性信号, 并使用零相位滤波器滤除25 Hz以上高频噪声, 可获得线性重构信号, 并可绘制线性重构信号与原始采样信号对比图, 如图6所示, 图中蓝色曲线为线性重构信号. 与原始采样信号相比, 线性重构信号的奇异值在40阶左右出现了明显的拐点. 伯德图中10 Hz与16 Hz的谐振得到清晰保留, 25 Hz以上无高频分量.因此可以用较低阶次的拟合函数或较少的神经网络节点辨识系统模型.

图6 线性重构信号与原始采样信号Fig.6 Linear reconstructed signal and original sampled signal

为验证系统辨识的简化效果, 使用仅包含10个节点的自回归神经网络辨识系统模型. 训练获得模型后, 向模型输入0–25 Hz扫频信号, 获得相应的响应信号, 如图7所示. 红色曲线为线性重构信号, 蓝色曲线为模型输出响应. 图8为该模型拟合的残差(Mean Squared Error, MSE), 可见残差在训练过程中迅速下降, 在200次训练后保持稳定, 残差最终约为1.65. 由此对比可以得出结论, 利用线性重构的数据替代含有非线性畸变的采样数据建模, 可以降低模型辨识的难度与模型的复杂程度, 提高模型辨识效率.

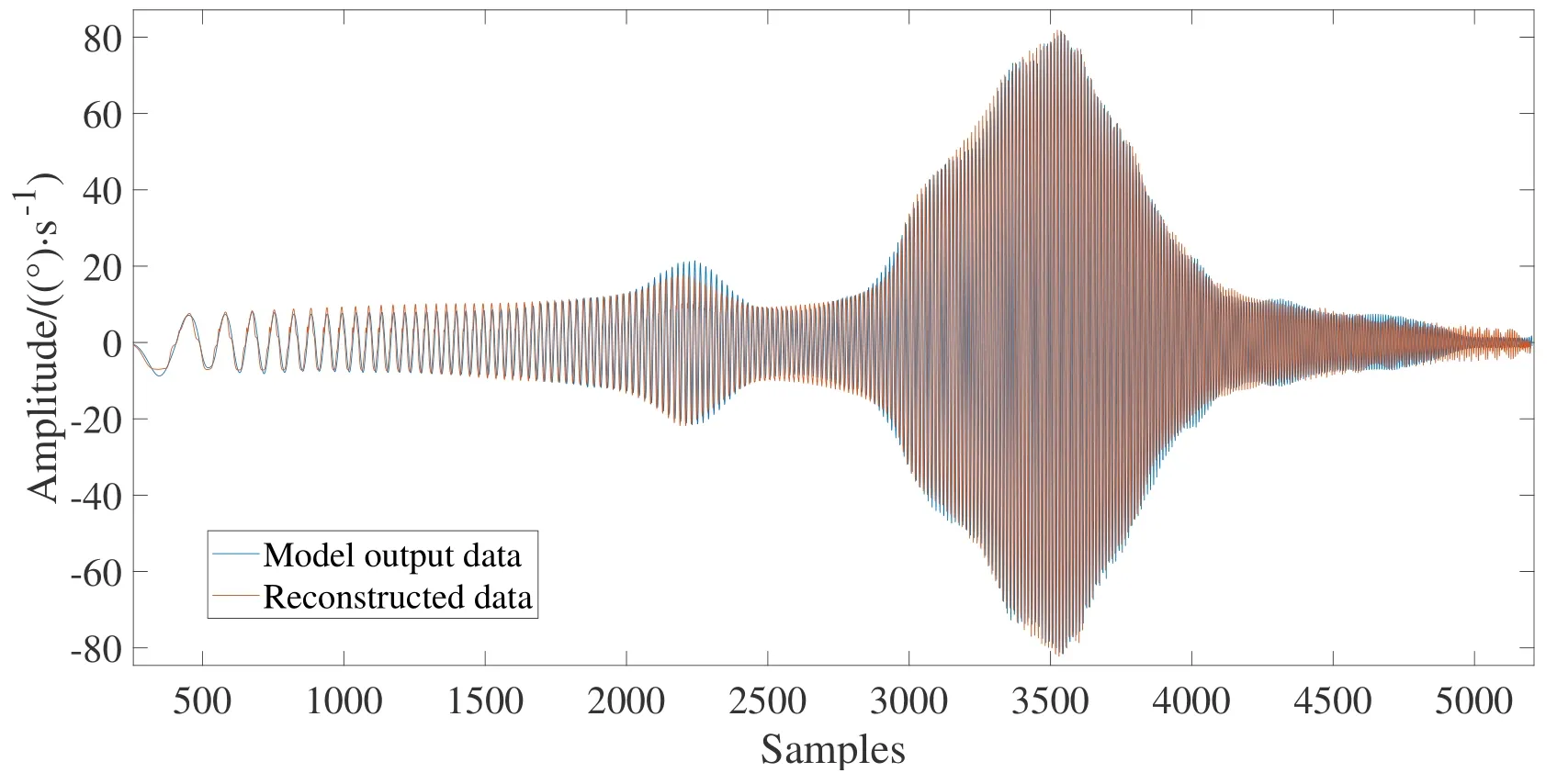
图7 线性重构信号与模型输出响应Fig.7 Linear reconstruction signal and model output response

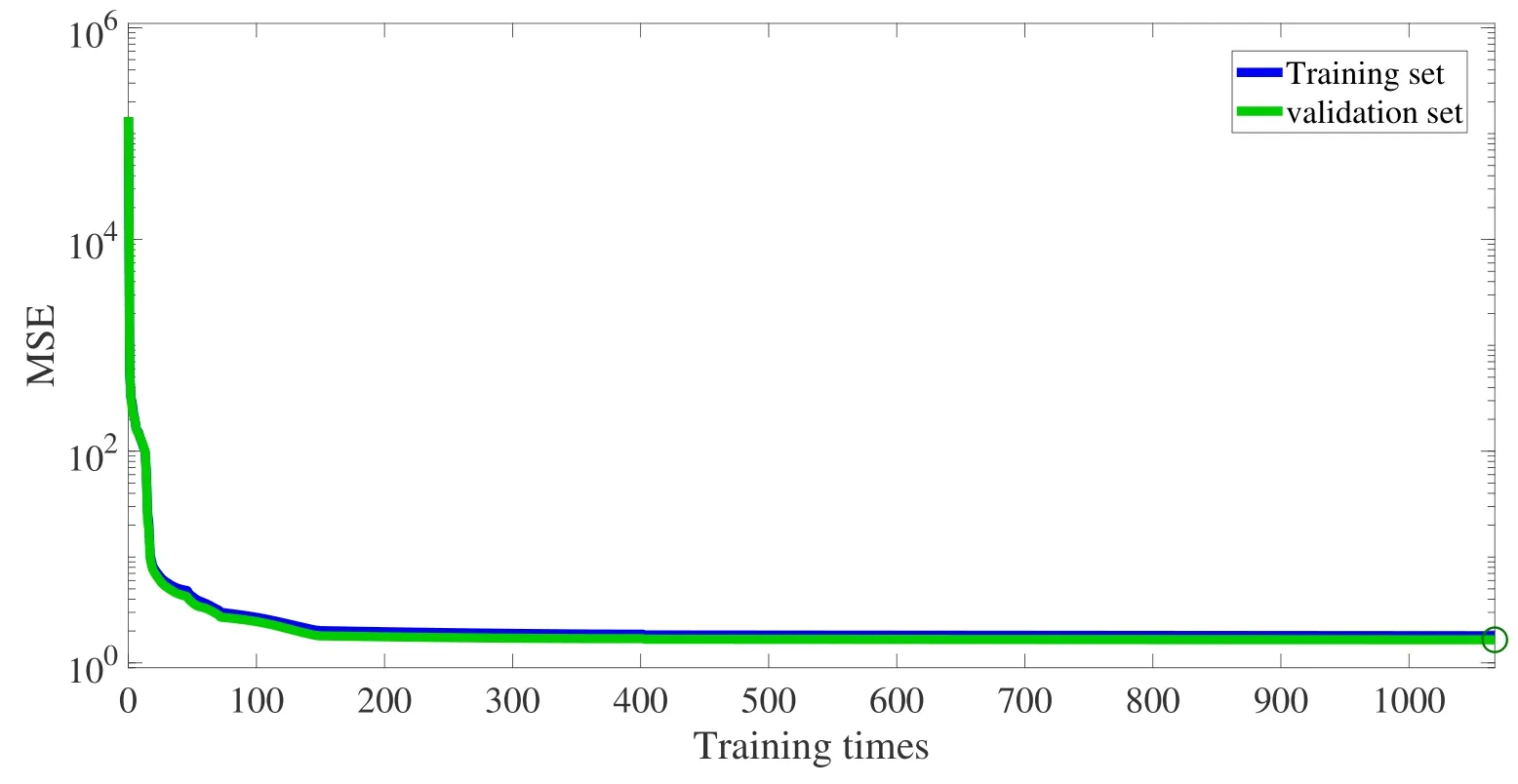
图8 辨识模型拟合残差Fig.8 Identification model fitting residuals

5 结论

为降低受到非线性影响的伺服控制模型辨识复杂程度, 采用线性数据重构与零相位滤波方法降低高频采样噪声与非线性畸变对采样数据的影响.通过半实物实验平台验证可知, 建模数据奇异值拐点从100阶下降至40阶, 仅用10个神经网络节点200次训练即实现了模型辨识, 在确保辨识精度的同时, 省去了系统非线性辨识与补偿的工作量, 降低了系统高频分量, 简化了辨识模型.