一种偏振定标单元方位角误差的约束非线性最小化优化定标方法*
闫 凯 郭 晶
(1 中国科学院国家天文台南京天文光学技术研究所南京210042)
(2 中国科学院天文光学技术重点实验室(南京天文光学技术研究所)南京210042)
(3 中国科学院大学北京100049)
(4 中国科学院大学天文与空间科学学院北京100049)
1 引言
在天文偏振测量研究中, 由于偏振系统自身各种误差带来的影响以及偏振仪器使用望远镜耐焦或折轴交点时光路的反射[1](即仪器偏振, Instrument Polarization), 会造成观测目标光的偏振态发生改变, 这直接影响了偏振测量的精度[2–3]. 偏振定标单元(Polarization Calibration Unit, PCU)作为一种定标仪器偏振[4–7]的重要装置, 它是实现天文高精度偏振测量的关键环节之一. 当今, 在太阳磁场观测领域, 国内外许多先进的太阳望远镜(例如1.6 m Goode太阳望远镜(Goode Solar Telescope, GST)[8]、4 m井上太阳望远镜(Daniel K.Inouye Solar Telescope, DKIST)[9]、我国1 m新真空太阳望远镜(New Vacuum Solar Telescope,NVST)[10]、1.8 m中国大型太阳望远镜(Chinese Large Solar Telescope, CLST)、2.5 m大视场高分辨率望远镜(Wide-field and High-resolution Telescope, WeHiT)与下一代8 m中国巨型太阳望远镜(Chinese Giant Solar Telescope,CGST)[11–13])都已配备了(或正在设计研制) PCU. 通常, PCU由一块线性偏振片和一块波片组成, 放置于太阳望远镜副镜的焦点附近, 通过控制PCU中两个偏振元件的光轴方位角旋转来产生多组不同的偏振态作为输出, 然后利用偏振系统对应测量各组偏振态, 最终可联合输出偏振态和测量偏振态来求解得到仪器偏振. 然而由于PCU中偏振元件的光轴方位角在生产和装配过程中会出现一定的误差, 导致输出偏振态会偏离其理论值, 从而降低了对仪器偏振的定标精度. 根据对PCU输出偏振态的计算分析,当线性偏振片和四分之一波片的光轴方位角误差在-1°至1°范围时, 斯托克斯分量的最大变化量将增加至10-2, 已经无法满足现代太阳物理对太阳磁场高精度偏振测量的要求(需达到10-3-10-4)[14].因此, 对PCU中偏振元件方位角误差的高精度定标是一项非常重要的研究工作, 它对于实现高精度偏振测量至关重要.
经分析可知, PCU中的误差来源主要包括: 偏振元件方位角误差、波片的线性二色性系数以及波片相位延迟量误差. 在对上述误差校准研究中,一种方法是非线性拟合定标法, 该方法将PCU中波片的方位角、相位延迟量以及仪器响应矩阵中的元素共同作为未知参数, 通过非线性拟合得到未知参数的值[15–16]. 在拟合过程中的自由变量(最多可达25个)、初值、优化方式等问题使得非线性拟合定标法较为复杂. 随后, 利用实际定标的仪器响应矩阵来进行改进, Beck等[17]使用该方法得到了线性偏振片与波片之间的方位角误差和波片线性二色性系数, 发现定标的方位角误差结果在红(630.15 nm & 630.25 nm)、蓝(396.8 nm)两个通道内的差异较大(达到6.14°); Hou等[18]使用该方法利用NVST在太阳光球谱线(Fe I 532.4 nm)的光谱偏振观测结果, 定标得到了线性偏振片与波片之间的方位角误差和波片相位延迟量的误差. 另一种方法是傅里叶分析定标法, 该方法能够对光学与探测器等器件的非线性因素进行修正[19–20], 包括PCU内偏振元件的光轴方位角误差, 线性二色性系数等影响因子, 该方法需考虑一阶误差对定标精度的影响, 且计算量很大. 本文在实验测得波片相位延迟量误差的条件下仅讨论方位角误差的定标方法与实验验证.
本文基于非线性拟合思路提出了一种基于约束非线性最小化的优化方法来定标PCU中的方位角误差. 首先, 将线性偏振片和四分之一波片的方位角误差(分别以Δθ1和Δθ2表示)作为两个待优化的自由变量, 同时限定它们在优化中的下限值和上限值. 然后, 利用产生和测量的Stokes参数以及偏振定标获得的响应矩阵定义优化目标函数. 最后,使用优化算法并在约束范围内实时计算目标函数值, 当满足停止条件后, 可以获得两个方位角的误差结果. 本文分别在理论模拟和实际测量中对提出的优化方法进行了验证, 先预设了几组方位角误差Δθ1和Δθ2, 再将优化得到的方位角误差Δθ′1和Δθ′2与它们的预设值进行比较. 实验结果表明, 通过此优化方法可以成功确定两个方位角误差Δθ1和Δθ2, 精度分别优于2.79′和2.72′, 且整个优化过程的速度很快. 本文结构安排如下: 第2节介绍了所使用的优化方法和相关算法, 第3节介绍了优化过程的实验设计, 第4节展示并分析了优化得到的两个方位角误差的结果, 结论在第5节中给出.
2 方法
本文中的偏振定标单元PCU由一个线性偏振片(Polarizer, P)和一个四分之一波片组成, PCU置于偏振仪的前端, 该偏振仪是本研究团队基于液晶可变相位延迟器(Liquid Crystal Variable Retarder, LCVR)研发的高精度成像偏振测量系统[21–22]. 首先,建立笛卡尔坐标系,X轴和Y轴分别沿水平偏振和垂直偏振方向, +Z轴为光线传播方向.以沃拉斯顿棱镜(Wollaston Prism,WP)的一个水平透光轴方向为基准(β1), PCU中的P和QWP的光轴方位角的理论值与实际值的误差角分别用Δθ1和Δθ2表示. 此外, 定义光轴在平行于X-Y平面上逆时针旋转的角度值为正, 反之为负. 如果不存在方位角误差, 则Δθ1和Δθ2等于0°. 偏振仪中的沃拉斯顿棱镜输出两束正交线偏振态的光束, 其两个光轴的方位角表示为β1和β2, 分别为0°和90°.PCU中的两个偏振元件、偏振仪中的WP和建立的坐标系的示意图, 如图1所示.
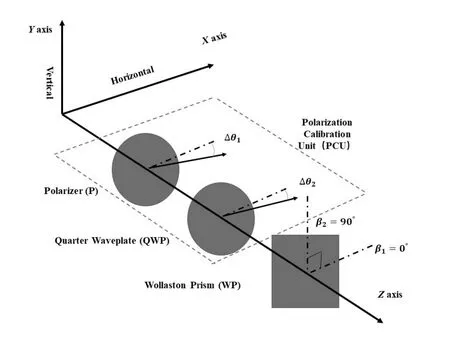
图1 偏振定标单元与沃拉斯顿棱镜的布局和方位角误差示意图Fig.1 Diagrammatic sketch of configuration and azimuth errors of the polarization calibration unit and Wollaston prism
根据偏振光理论[23], 参考系在垂直于光路传播方向的平面上逆时针旋转角度θ, 可表示为如下矩阵:

其中c2= cos 2θ,s2= sin 2θ,θ是参考空间的旋转角度. 旋转参考系后的穆勒矩阵可以用如下矩阵表示:
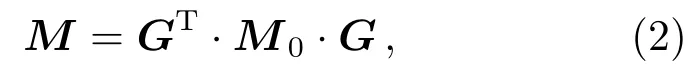
其中G=MROT(θ),M0表示当偏振元件光轴方位角为0°时的穆勒矩阵.
P和QWP的穆勒矩阵分别表示为:
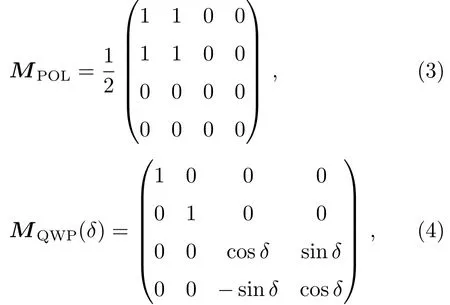
其中δ是QWP的相位延迟量.
根据(1)–(4)式, 可以推导得到P与QWP的光轴旋转后的穆勒矩阵:
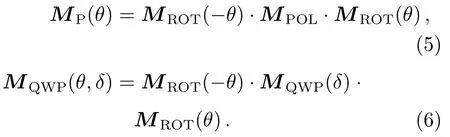
当入射光透过偏振元件, 若M表示偏振元件大小为4×4的穆勒矩阵,S表示输入光的初始偏振态, 则输出光的偏振态S′可表示为:

当光经过n个偏振元件组成的系统, 按照k=1,2,··· ,n这个顺序, 每个元件都有一个穆勒矩阵Mk, 则整个系统的穆勒矩阵为:
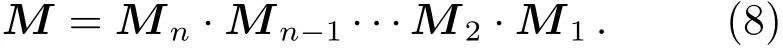
当使用非偏振输入光并旋转QWP时, PCU可以根据需要来产生多组不同的标准偏振态, 并且可以根据穆勒矩阵计算输出的偏振态:
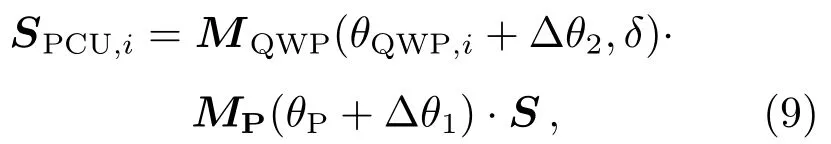
其中θP+Δθ1和θQWP,i+Δθ2分别代表P和QWP光轴方位角的实际值, 其内包含了两个方位角误差Δθ1、Δθ2,θP和θQWP,i分别代表线性偏振片和四分之一波片预设的理论值.i是QWP旋转角度的序号,S可以表示为S= (I,0,0,0)T, 其中I表示测量辐射的强度.
当θP等于0°, PCU的输出可以表示为:
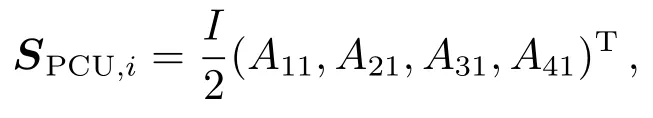
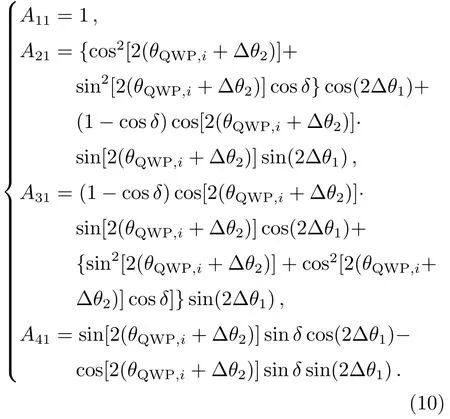
令QWP的光轴方位角从0°旋转到180°, 转动步长为5°, 则PCU将产生并输出37组标准偏振态.根据偏振系统输入和测量得到的偏振信息, 可以得到如下关系式:
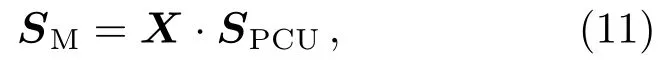
其中SPCU是PCU输入的斯托克斯向量,为4×37的矩阵.SM是偏振仪测量的斯托克斯向量, 其矩阵大小与SPCU相同.X是偏振仪的响应矩阵, 其大小为4×4.SM和SPCU为已知量,X为未知量, 根据(11)式可计算得到X. 由于SPCU为非方阵, 所以通过(11)式计算偏振仪的响应矩阵X时, 需采用奇异值分解(Singular Value Decomposition, SVD)方法.
从上述计算可以看出, 校准两个方位角误差Δθ1和Δθ2可以提高PCU的偏振态输出精度, 进而能够更加准确地得到响应矩阵X. 由于PCU中QWP的相位延迟量存在误差, 针对实验光源波长(@632.8 nm)对QWP进行了相位延迟量定标测量,重复测量20次, 得到波片相位延迟量的平均值为90.1478°, 实验中Δδ=0.1478°. 本文提出的优化方法将方位角误差Δθ1和Δθ2作为两个待求解的自由变量, 然后定义一个目标函数f作为优化中的评价函数:
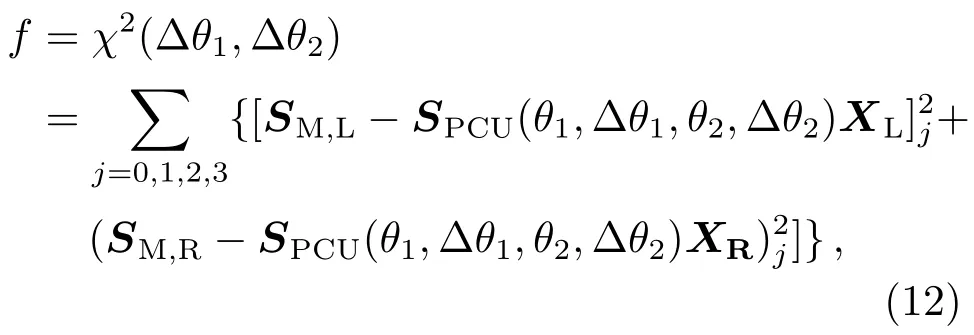
其中SM,L和SM,R分别是Wollaston棱镜分光后的左、右光束的斯托克斯向量, 均为37×4的矩阵.XL和XR分别对应左、右光束计算得到的偏振仪响应矩阵,j表示大小为37×4矩阵的第j列.
经分析, 目标函数f是非线性函数,θ1和θ2是依据偏振方案设计确定的已知量, 它们分别是(9)式中的θP和θQWP,i, Δθ1和Δθ2是待优化自由变量, 且δ为90.1478°已经作为常量代入到目标函数f中. 在优化开始前, 预设Δθ1和Δθ2在优化中的边界, 均约束于优化变量的下边界值A和上边界值B之间,在优化过程中, Δθ1和Δθ2的值会在其约束范围内自动调整. 当SM,L-SPCU(θ1,Δθ1,θ2,Δθ2)XL和SM,R-SPCU(θ1,Δθ1,θ2,Δθ2)XR的值逐渐减小至最小时(接近于0), 表示两个方位角误差Δθ1、Δθ2已逼近它们的实际值. 则通过提出的优化方法可以确定得到Δθ1和Δθ2:
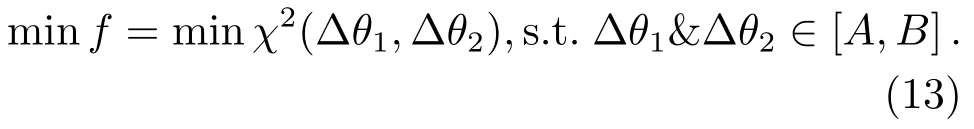
非线性问题通常转化为更容易求解的序列二次优化问题, 而序列二次规划(Sequence Quadratic Problem, SQP)算法是解决非线性问题的重要方法[24]. 在优化过程的每次迭代中, 通过求解一个二次规划子问题来确定优化下降方向, 从而减小了评价函数值, 不断重复这些步骤, 直到获得原始问题的解[25]. SQP算法的优点是它具有良好的收敛性,对于解决有约束的优化问题非常有效[26], 所以在本研究中使用了SQP算法.
3 实验设计
3.1 优化实验流程
根据第2节的优化方法设计了定标方位角误差的优化实验, 其流程如图2所示. 优化实验将从理论模拟和实际测量两个方面进行开展, 然后根据实验结果对优化方法的可行性与性能进行验证与评价.
在图2中, 右侧矩形框内的符号1表示理论模拟时使用的响应矩阵, 符号2表示实际测量时使用的响应矩阵. 首先, 通过控制独立旋转的高精度电动旋转座来预设产生两个角度Δθ1和Δθ2. 然后, 将QWP的光轴方位角以5°步长从0°逐渐转动至180°. 通过这种方法, PCU可以输出37组偏振态并输入到偏振仪, 然后对其输出的左、右光束的偏振斯托克斯参数进行理论模拟和实际测量. 其中,在理论模拟中设置XL和XR为单位矩阵, 在实际测量中设置XL和XR为偏振定标中获得的实际矩阵(根据(11)式计算得到, 且计算中QWP的相位延迟量为实验测量值). 最后, 将它们代入优化的目标函数(12)式, 通过优化算法求解获得两个方位角误差值Δθ′1和Δθ′2.
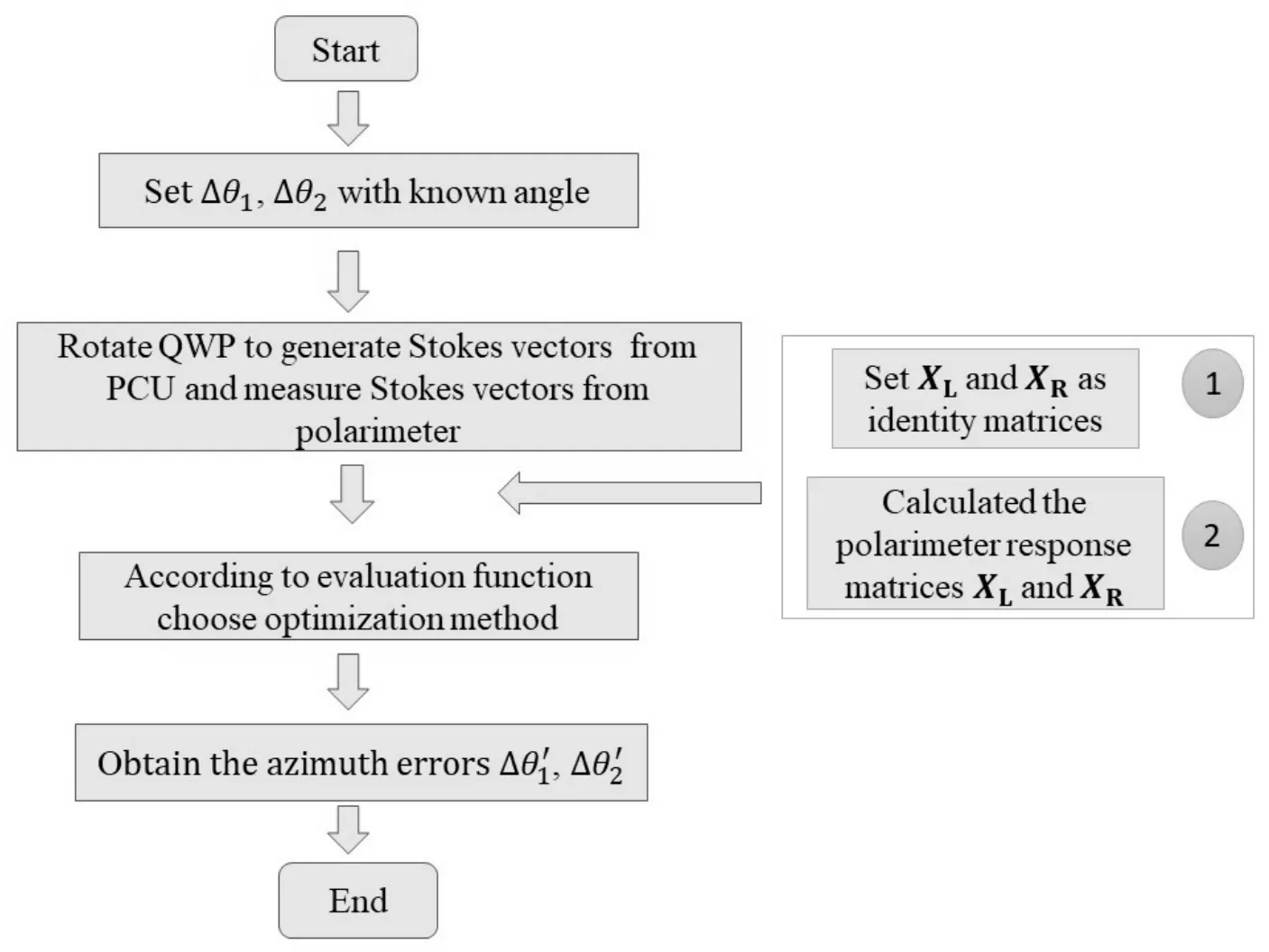
图2 确定方位角误差的优化方法的实验流程图Fig.2 The flow chart of the experiments of the optimization approach to determine the azimuth errors
3.2 试验系统的组成
为了验证提出的优化方法, 在实验室建立了如图3所示的实验平台. 首先, 由He-Ne激光器(波长632.8 nm)、针孔和显微物镜组(图3中未展示)产生非偏振的点光源, 随后经透镜(L1)准直. 然后, 光束通过由P和QWP组成的PCU. P和QWP分别安装在一个独立的高精度电动旋转座上, 可通过步进电机进行控制光轴的旋转角度. 接下来, 光束入射到由一对液晶可变相位延迟器(LCVR1&LCVR2)组成的调制单元(Modulator Packages, MP). LCVR的相位延迟量是根据电压控制, 利用电压控制器控制LCVR, 使其输出指定的相位延迟量.两个LCVR可以设置6组固定相位延迟量组合, 形成6种调制模式[22]. 由于LCVR对温度变化敏感, 所以控制其工作温度稳定在24.9°C±0.5°C, 并且在该温度下对两块LCVR预先标定. 在实验开始前将LCVR预热约15 min以获得更好的稳定性.随后, 光束经过WP, 由WP出射的两束光振动方向相互垂直且分离角大约为1°. 最后, 由WP分光形成两个正交偏振态的光束经透镜(L2)成像在相机(CAM)的焦面上. 此外, 基于LabVIEW开发了专用软件来控制步进电机、LCVR和相机, 同时也基于MATLAB开发了偏振数据处理与解调软件, 其中已包含了暗场校正和平场校正等步骤.

图3 用于优化实验建立的试验平台Fig.3 Experimental platform established for the optimization experiment
实验系统中使用的元器件的技术参数, 如表1所示, 其中λ为波长.
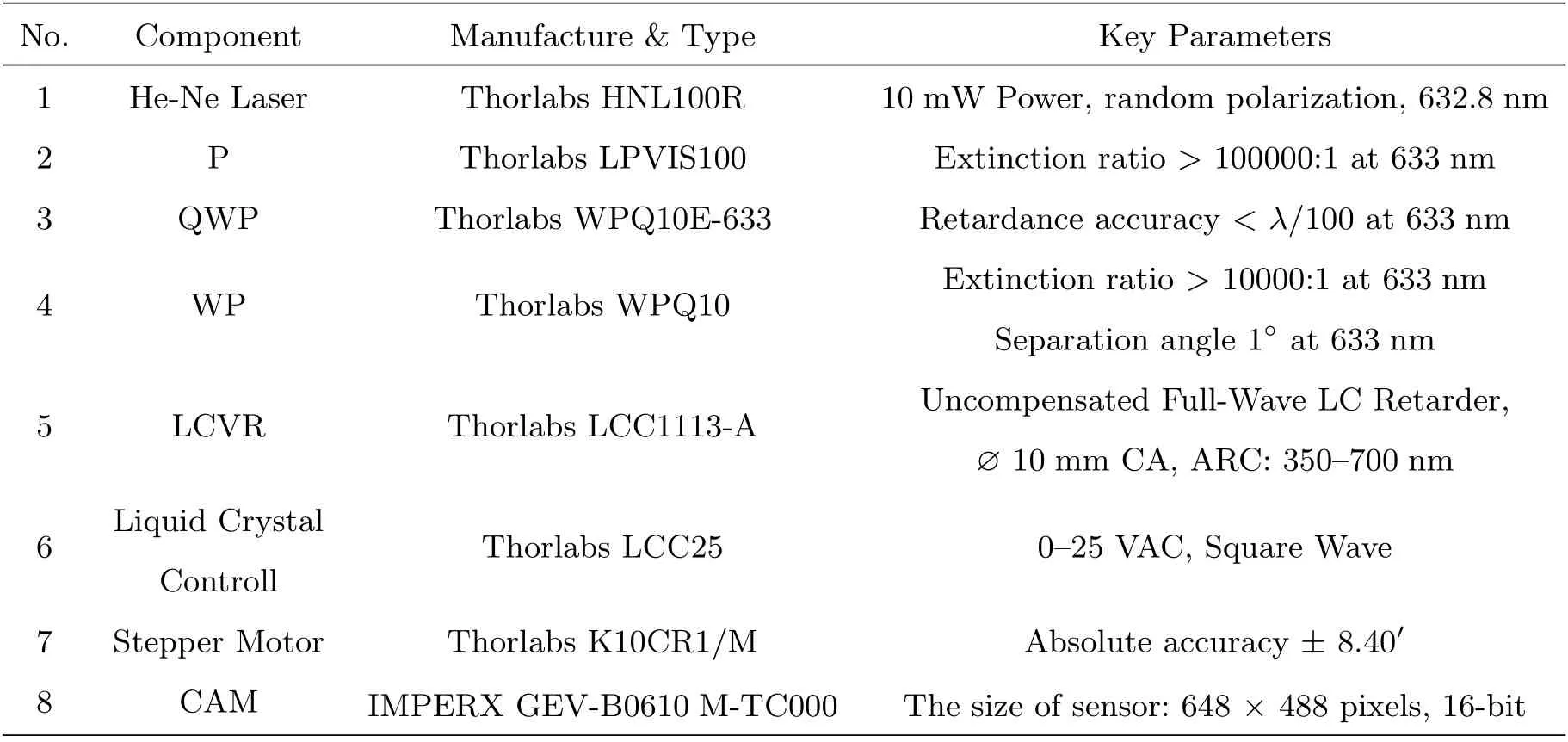
表1 优化实验中主要元器件的参数Table 1 Specifications of the main components used in the optimization experiment
4 结果与讨论
4.1 优化方法的性能
以预设条件Δθ1= 0和Δθ2= 0为例, 优化时将两个方位角误差的下限和上限分别设置为-2°和2°. 需要注意的是, 预设Δθ1= 0和Δθ2= 0不影响优化算法有效性的验证(更多其他预设值验证结果在4.2节中给出), 另外, 扩大Δθ1和Δθ2的上下限不会改变最终的优化结果, 若设置的初始点偏离优化的目标点, 只是需要消耗更多的计算时间. 一旦满足优化的停止条件, 即目标函数达到最小值(限制条件下), 优化停止, 并得到通过优化方法确定的Δθ′1和Δθ′2. 图4显示了优化过程中目标函数值随迭代次数的变化情况. 优化中的一阶最优性度量的容差(Optimality tolerance)设置为10-6.
在图4中, 目标函数值在第6次迭代之前迅速减小, 然后开始逐渐下降. 经过约21次迭代后, 一阶最优性度量的容差稳定在1.397×10-9, 优化停止,目标函数的最小值是0.03844. 根据优化变量合理的限制范围和初始点以及目标函数的选择, 使得使用SQP算法具有良好的收敛能力, 且收敛速度快,整个优化过程可以在10 s内完成.
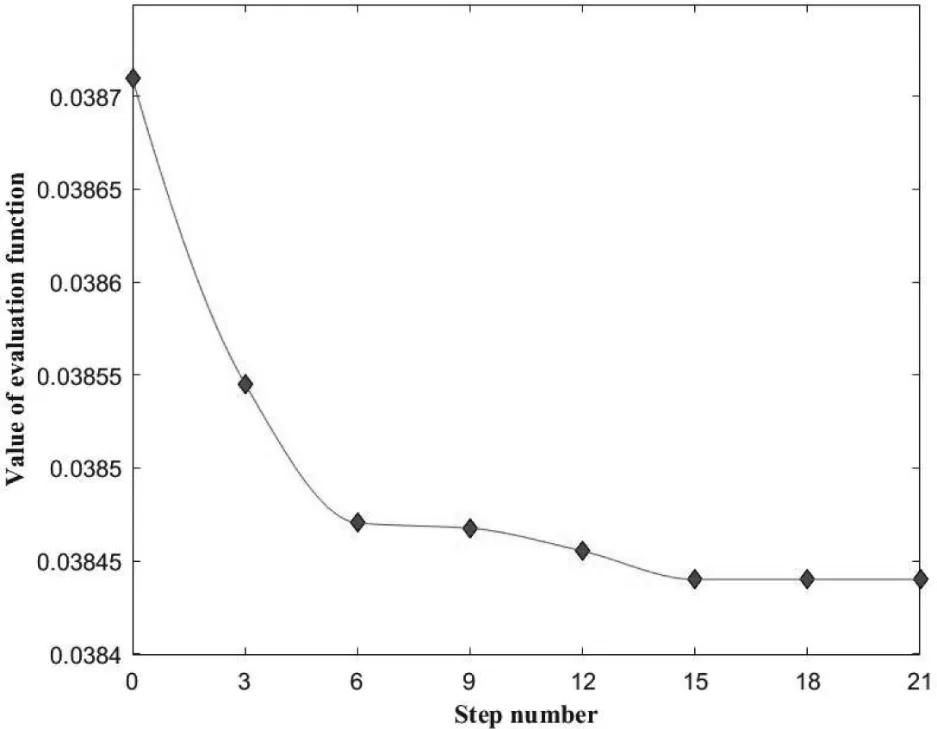
图4 优化过程中的目标函数值变化Fig.4 Variation of values of the objective function during the optimization process
4.2 优化实验结果
为了说明优化方法的可行性与性能, 在实验中测试了几组不同预设值的方位角误差Δθ1和Δθ2,并涵盖了不同的误差角方向(正向、负向). 考虑到步进电机的绝对旋转精度为8.40′, 于是将两个方位角误差的预设值设为9.00′的倍数, 实验范围从-36.00′到+36.00′. 然后, 分别得到了方位角误差的理论模拟()和实际测量(Δθ′1,E,Δθ′2,E)两方面的结果, 如表2所示. 表2中的每组结果为重复5次实验得到的平均值.
表2的实验结果表明, 本文优化方法可以成功确定两个方位角误差. 在理论模拟结果中,的值等于其预设值Δθ1和Δθ2, 这是因为左、右光束的响应矩阵(即(12)式中的XL和XR)均被设置为单位矩阵. 在实际测量的结果中,优化方法仍然有效, 得到的Δθ′1,E和Δθ′2,E与Δθ1和Δθ2预设值非常接近, 两个方位角误差的精度,a和b分别代表实验和误差角的序号分别优于2.79′和2.72′.此外,该优化方法也能够正确示出方位角误差的方向(正向或负向),这将有助于装调和校准PCU中的偏振元件.

表2 优化方法确定的方位角误差结果Table 2 Experimental results of azimuth errors determined from the proposed optimization approach
4.3 方位角误差对斯托克斯参数影响的理论分析
本节进行方位角误差对斯托克斯参数影响的理论分析. 首先指定两个方位角误差Δθ1和Δθ2的变化范围, 然后计算分析斯托克斯参数的变化(Δ(Q/I), Δ(U/I), Δ(V/I)),Q表示水平方向偏振分量的强度,U表示方位角为45°方向上的偏振分量强度,V表示圆偏振分量的强度. 其中,θ1和θ2设置为0°, Δθ1和Δθ2从-1°到1°变化, 其模拟结果如图5所示.
从图5 (a)中可以看出, 当两个方位角误差Δθ1= 1°和Δθ2=-1°(或反之)时对Q/I的影响最大,此时Δ(Q/I)的值为-3×10-3. 这是因为具有相反方向的两个方位角误差将导致最差的定标性能.此外, 当Δθ1和Δθ2的方向相同且Δθ1= Δθ2= 1°(或-1°)时,Δ(Q/I)的值为-6×10-4.在图5(b)中,当Δθ1和Δθ2两 者 都 等 于1°(或-1°)时 对U/I值 的影响最大, Δ(U/I)的最大(或最小)值为0.0353(或-0.0353).当Δθ1=1°和Δθ2=-1°(或反之)时,Δ(U/I)的值变为-0.0344 (或0.0344). 在图5 (c)中,当Δθ1= 1°和Δθ2=-1°(或反之)时,V/I最大变化的绝对值为0.0698. 此外, 如果Δθ1与Δθ2相等, 则不会对V/I产生影响, 即Δ(V/I) = 0. 这是因为将Δθ1= Δθ2代入(10)式时, 圆偏振分量的值不会变化, 即圆偏振分量值的变化量为零.由以上分析可知, 两个方位角误差Δθ1和Δθ2对斯托克斯参数有明显影响, 在-1°到1°变化范围内Δ(U/I)和Δ(V/I)的值已增加至10-2量级, 因此,需要在实际定标和校正过程中特别注意元件方位角误差的定标, 而利用本文提出的约束非线性最小化的优化方法可以很好地解决该问题.
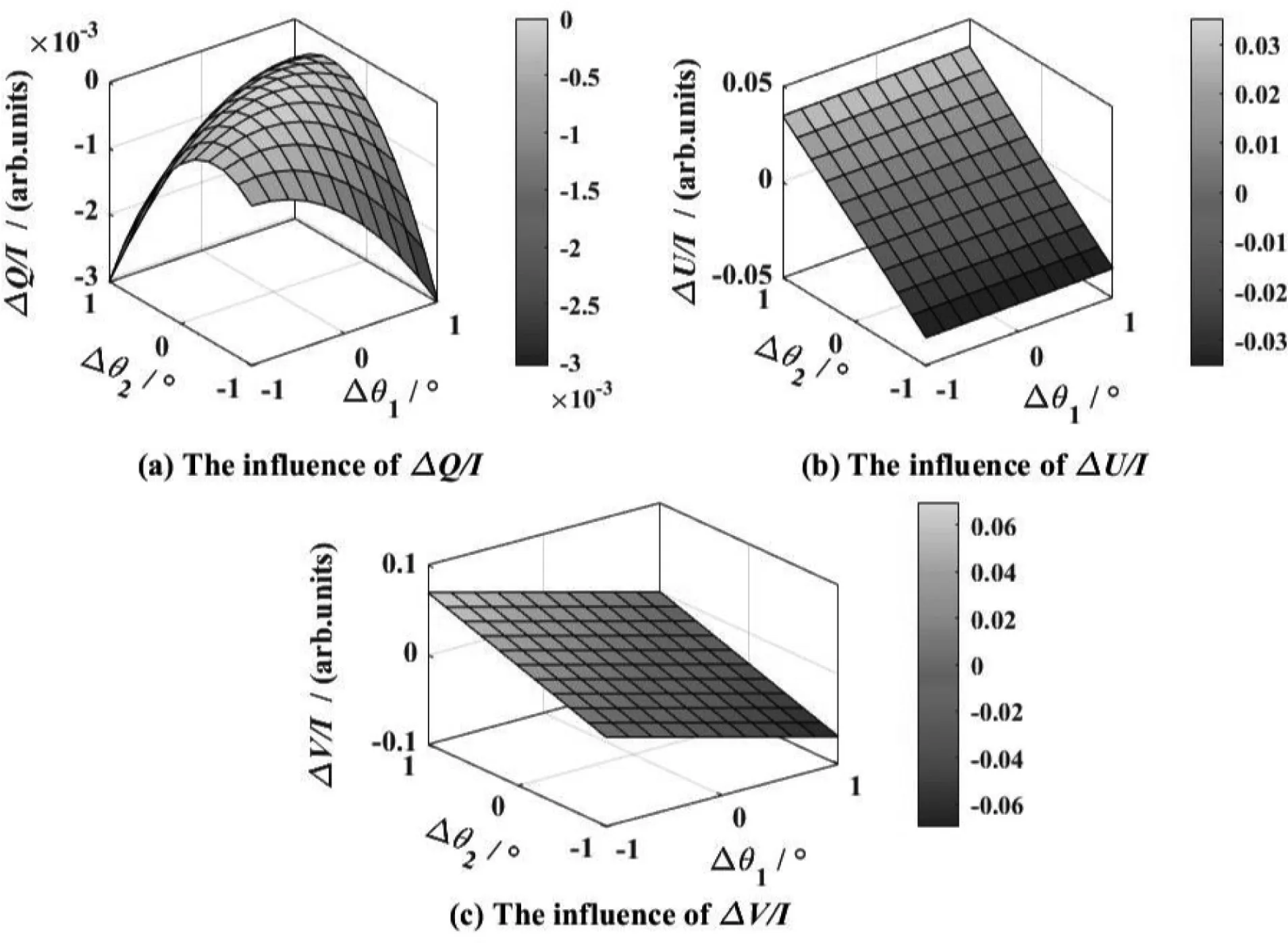
图5 两个方位角误差对归一化的Stokes参数的影响Fig.5 Influence of the two azimuth errors on the normalized Stokes parameters
5 结论
标定偏振定标单元中的方位角误差对于提高偏振态的输出精度, 进而更加准确地获得偏振系统的响应矩阵和开展高精度偏振测量具有重要意义. 本文提出了一种基于约束非线性最小化的优化方法定标方位角误差值, 并分别从理论模拟和实际测量两个方面对所提出的优化方法进行了验证. 实验结果表明, 该优化方法可以成功求解出偏振定标单元中线性偏振片和四分之一波片的方位角误差Δθ1和Δθ2, 精度分别优于2.79′和2.72′, 并且还可以示出方位角误差的方向(正向或负向), 这将有助于偏振元件方位角的装调和校准. 此外, 该方法还具有优化速度快的优点. 本文研究工作希望能够为高精度偏振定标与应用铺平道路, 并有望应用到我国太阳望远镜中偏振定标装置的误差定标及研制之中[27–29]. 本文方法具有良好通用性, 可拓展至定标其他偏振测量领域(遥感和探测、显微测量和大气研究等)中偏振仪的PCU[30–35].
致谢感谢审稿专家对本文提出的宝贵意见与修改建议, 感谢课题组各位老师的帮助.

