天体轨道长期数值积分的误差估计方法

宋浩冉 黄卫东

(中国科学技术大学环境科学与工程系合肥230026)

1 引言

数值积分方法是进行天体力学研究的重要工具, 尤其对于精密行星历表的计算工作而言极为关键. 当使用数值积分方法计算实际轨道时, 计算误差的产生与增长是无法避免的, 且受积分方法与积分步长选择的影响[1].

不同积分方法的性能特点与适用范围大不相同[2]. 如Adams型线性多步法1包括用于求解一阶微分方程的Adams-Bashforth (显式)方法和Adams-Moulton (隐式)方法, 与求解二阶微分方程的St¨ormer (显式)方法和Cowell (隐式)方法. 计算时可将上述两类方法联用, 称为Adams-Cowell方法.方法[3]及其派生算法的主要特点为高阶方法易于构造, 运算复杂度远低于其他同阶方法且不随阶的升高而增加, 但仅适合用于低偏心率轨道[2]. Everhart方法[3]在计算效率上虽然难以与Adams-Cowell方法相比,但作为一种单步法其适用范围几乎可以涵盖所有情形, 且高阶方法同样相对易于构造, 十分适合用于高偏心率轨道或其他刚性问题的求解[2]. 以上两种方法具有一个共同缺陷, 即不保辛. 因此, 在使用以上两种方法对天体轨道进行长期积分过程中会使轨道发生偏离从而导致解的失真, 故对于一些研究天体轨道长期演化为主的工作而言, 辛算法是最为合适的选项[4], 如Laskar等人的系列工作[5–6]即采用基于摄动分解的MVS (Mixed Variable Symplectic)型辛积分器进行计算[7–8].

但在面对具体的轨道计算任务时, 仅能确定使用哪类算法是远远不够的. 比如当选择使用Adams型线性多步法进行积分时, 可供选择的具体积分方法是非常多的,除经典Adams-Cowell方法外还有Krogh方法[9]与KSG2KSG是其3位作者Krogh-Shampine-Gordon的缩写.积分器[10–11]等诸多算法与积分器. 而当选择使用MVS型积分器时可供选择的具体算法更是不胜枚举[12–14]. 即使在选定具体算法后, 仍需对所选方法的阶以及步长选择进行讨论, 而误差水平则是进行这一系列讨论工作时所要重点参考的一个指标. 因此在面对实际问题时, 对积分过程中所产生的各项误差进行较为精准的评估对于具体积分方法与积分步长的选择而言十分重要.

通常情况下, 进行误差评估的时间节点可以有3个, 分别为在计算完成后、计算过程中以及计算开始前. 其中最为常见的误差估计方式即在计算完成之后进行估计, 通常会将理论值与计算结果进行对比以获取误差估计值, 这也是最为常用且最为可靠的误差估计方法. 用于对比的理论值可以是高精度的观测值, 也可以是解析解. 但对于需使用数值方法求解的问题而言, 在大多数情况下没有可供参考的理论值, 此时一般会选择使用更高精度的数值解与之进行对比的方式来估计其误差. 使用这种方法进行误差估计是最为准确的, 但其所需引入的额外计算量可能数倍甚至数十倍于原算法, 其代价也是最大的. 因此, 在行星历表的计算工作中,此方法通常仅用于积分方案选择及步长选择的研究(如INPOP06历表积分步长的决策过程[15]),一般仅在有现成高精度解可供参考时可对其积分时间范围重叠部分的计算结果精度进行对比研究(如在La2010解中即采用了更高精度的INPOP06与INPOP08解进行校正[6]).

在计算过程中的误差同步估计是指在计算过程中对过程中所产生的误差进行同步计算, 通常仅用于截断误差的判断. 由于大部分常用积分方法的局部截断误差都有确切的表达式, 故理论上每一步计算所产生的截断误差都是可知的. 因此当局部截断误差可以使用已知量进行构造或近似表达时,即可采用这种方法对截断误差积累量进行估计,如当使用线性多步法方法(见文献[4]中369–370页)或Runge-Kutta-Fehlberg方法[16]时. 对于不同算法而言构造局部截断误差的难易程度不同, 故此方法通常对于某些构造起来较为容易的算法而言较为适用, 但当使用这种方式所需引入的额外运算量较大时则须慎重考虑.

以上两种方法虽然可以较为精确地获取计算误差, 但其共同缺点为均不能在计算之前对最终误差进行预判. 因此, 当对最终误差的容许范围有明确要求时, 只有在计算完成之后才能知道最终计算结果是否可以满足精度需求, 而这无疑会带来极大的不确定性. 尤其是在面对计算量极其庞大的工作时(如行星历表的研制工作), 这种不确定性所带来的影响可能是十分严重的. 在这种情况下, 能在计算开始之前就对将产生的误差总量进行较为精准的预判就显得非常重要, 但目前尚未有能在计算开始前即能对误差进行估计的成熟方法.

本文即通过对计算误差的两大重要组成部分–舍入误差与截断误差的增长速度及其随步长的变化规律进行了系统性的研究. 基于所得结论我们提出了一种在仅需极少数值实验资料的基础上即可对使用特定积分方法时选择任意步长积分至任意时刻产生的总体误差的概率密度分布函数进行估计的方法,并以使用Adams-Cowell方法为例对该误差估计方法在圆轨道沿迹方向上的误差估算精度进行了数值验证. 该方法未来可用于具体数值积分方法的性能研究, 且可以为精密行星历表的研制工作提供帮助.

2 误差来源

在使用数值方法计算实际问题时的误差来源往往十分复杂. 相对于真实情况而言, 数值解的误差可分为模型误差与计算误差两大部分, 其中模型误差指用于计算的物理模型与真实情况之间的差距所带来的误差, 而计算误差则指在按照给定物理模型进行求解的过程中所产生的误差. 由于模型误差与所采用的具体数值方法无关, 因此本文不对其进行讨论.

计算误差的来源分类没有一个统一的标准, 从不同角度出发可以有不同的分类方式.Higham[1]将误差来源分为计算过程中的舍入误差、数值方法的截断误差以及数值不确定度3大类, 其中又将数值不确定度进一步细分为了来自于测量或者估计所带来的不确定度、计算机存储过程中产生的舍入误差以及通过误差传递从先前过程中的误差中获取的误差(见文献[1]中5–6页). 从这一分类方法上, 我们可以发现除通过误差传递所得到的误差之外的其他各项误差相互之间均不受其他类型误差的影响, 因此可以线性叠加. 而通过误差传递所得到的误差的大小则依赖于先前已有的误差. 由于在误差传递过程中, 原有误差可能会被放大, 也可能缩小或者不变, 即在此过程中可能有新的误差生成. 我们可以将这一过程形象地用以下公式进行表示:

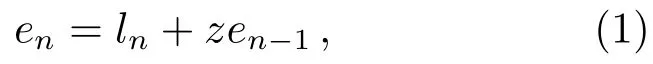
其中en为第n步处的全局误差,en-1为第n-1步处的全局误差, 公式右侧ln指该步运算中与误差传递过程无关的所有新生成的误差,zen-1则代表的是从上一步中传递而来的误差, 其中z是误差传递系数, 通常可以表示为复数. 其中, 若能满足z=1, 则表示误差不会随着传递过程放大或缩小, 此时全局误差即等于之前每一步所产生的原生误差的线性叠加. 此时en则可表示为

其中,l0指初始误差, 即初始的输入值中由测量或者估计所带来的不确定度,i为哑指标.

当z /=1时, 则有

如此一来, 如上式所示, 全局误差即可分为两大部分, 其中我们将第一部分称之为原生误差, 即除去因误差传递过程中所产生的额外误差之外的所有误差, 其组成较为复杂. 另一部分则可以相应地称之为次生误差, 即在误差传递过程中所额外产生的误差. 下面我们将分类对以上各类误差的产生机制与性质进行简要介绍.

2.1 原生误差

若按照Higham[1]对计算误差来源的分类方法进行定义, 此处原生误差应包括计算过程与计算机存储过程中所产生的舍入误差、数值方法的截断误差以及来自于测量或者估计所带来的不确定度.其中对于数值积分过程而言, 测量或者估算所带来的不确定度的引入仅存在于初始值中, 因此若仅针对数值积分过程, 原生误差来源可以简单划分为初始误差、舍入误差与截断误差3大来源. 其中初始误差仅与初始值的获取过程有关, 与计算过程无关, 因此本文在此不对其进行讨论.

2.1.1 舍入误差

舍入误差是在数值计算过程中最值得关注的误差来源之一. 关于这一类误差的研究早在19世纪末就已经开始了[17]. Higham[1]将舍入误差分为了两类, 其中计算过程中所产生的舍入误差主要是因为在计算过程中能够保留的有效数字个数有限, 因此在计算时必须对计算结果进行舍入, 由此导致了舍入误差的产生. 而计算机存储过程中所产生的舍入误差则有多种可能: 一种可能性是由于计算机的存储精度是有限的, 如果计算精度高于存储精度则会导致舍入操作的发生, 从而产生舍入误差; 另一种可能性是在计算机尚未全面普及的情况下许多计算需要手动在十进制下进行, 而大多数十进制小数是不能用有限精度的二进制浮点数进行精确表达的, 因此导致舍入误差的产生. 而在计算机已经全面普及的今天, 数值积分过程中一般都是全程在计算机上进行的, 而数值在计算机中的不同存储元件中搬移或进行数据类型转换的过程本就可以看作一种计算, 在此背景下已没有对这两类舍入误差进行严格区分的必要, 因此本文将此二者归为同一种误差.

舍入误差的生成通常被认为是服从高斯分布的[18–19]. 由于在计算机的数值计算过程中一般默认采用就近舍入的策略, 因此新产生的舍入误差的期望一般为0. 由于独立正态分布在进行四则运算时其结果依然为高斯分布, 且其计算结果的期望等于参与运算的各分布函数的期望直接代入计算所得的值, 因此在一般情况下复杂运算所产生的舍入误差同样服从期望为零的高斯分布.

另外, 虽然舍入误差服从高斯分布, 但这并不意味着舍入误差是一种随机误差. 相反舍入误差是一种确定性误差, 即对于同一计算过程在任何输入条件都不变的情况下, 计算至任意一步时产生的舍入误差都是确定的(见文献[1]中48–49页). 但由于舍入误差是一种对输入条件极其敏感的误差, 因此该误差具有混沌特性, 这也是许多人误认其为随机误差的原因. 基于舍入误差的这一特性, 在使用数值方法进行实际问题的求解时, 可以通过对部分输入条件进行调整, 并通过大量的试错过程来对舍入误差的积累量进行人为干预, 因此舍入误差的这一特性如果运用恰当则可以有效控制计算误差的增长速度(如INPOP06的步长选择即充分利用了这一特性[15]). 同时, 舍入误差的这一特性也意味着在对具体计算过程的舍入误差进行研究时无法在输入值不变的情况下通过重复实验获得其分布规律, 而若改变输入值则会引入其他变量, 同样无法用于进行舍入误差分布规律的研究. 因此对于确定的实际问题求解过程而言, 获取其舍入误差分布的变化规律是一项非常困难的工作, 这也给数值方法的性能研究工作带来了非常大的阻碍. 如果能够攻克这一难题, 则可以对积分器性能的比较研究带来极大帮助, 具有十分重要的现实意义.

2.1.2 截断误差

截断误差的产生是使用差分方法求解微分方程所导致的. 理论上, 当不考虑数值计算过程的时间成本的情况下, 局部截断误差理论上可以无限接近于零, 但这样做的代价便是所需计算时间将趋于无穷大, 因此截断误差的存在是计算精度向计算效率妥协的必然结果.

影响局部截断误差大小的因素主要有两个: 一个是方法的阶, 另一个是积分步长. 通常情况下, 方法的阶越高, 步长越小, 则计算精度越高, 局部截断误差越小. 因此若想增加解的计算精度通常可以通过升阶或缩短步长的方法实现. 但在实际情况下,通过以上两种方式提高精度并不总是可行的. 缩小步长一方面会使工作的总体计算量增加, 另一方面会造成舍入误差的增加. 而采用升阶的方法除了会增加线性多步法以外的绝大多数算法的计算量外,对于部分算法而言也可能会加速舍入误差的增长.最为重要的是, 当前能够较为容易地获得高阶方法的数值积分方法并不多, 在天体轨道计算中比较常见的仅有Adams型线性多步法与Everhart方法两种[2]. 另外对于Adams-Cowell方法而言, 升阶会严重影响最大积分可选步长, 这也极大限制了其通过升阶提升算法性能的潜力[20].

因此, 在使用数值积分方法解决具体问题时,选择合理的积分方法的阶与步长对于误差控制而言非常重要, 值得深入研究. 由于截断误差同样是一种确定性误差, 且对于除BS算法[21]之外的绝大多数算法而言, 局部截断误差都有确定的表达式,因此在选择使用满足上述条件的定阶定步长方法时, 积分过程中所产生截断误差积累量理论上是可知的, 这就使得对截断误差积累量随步长甚至于阶的变化规律的研究具有理论上的可行性. 如果能够掌握这一规律, 则可以在必要时极大缩短在使用数值方法计算实际轨道问题时对具体积分方案选择所需的时间, 从而提高决策效率.

2.2 次生误差(不稳定性导致的额外误差)

此处的次生误差指的是误差传递过程中产生的误差膨胀现象所带来的额外误差, 关于这一现象的研究通常被称为稳定性研究. 误差膨胀通常是对数值计算精度影响最为严重的误差来源, 因其通常呈指数增长, 故可以使数值解快速失真. 造成这一问题的原因主要有两个: 一个来源于具体采用的数值方法, 另一个来源于方程本身. 与前者相关的稳定性问题通常被称为数值方法稳定性问题, 而与后者相关的稳定性问题则称为李雅普诺夫稳定性问题.

数值方法稳定性通常与积分步长h的选择有关. 当求解形如y′=λy的一阶微分方程时(λ为复数), 误差传递系数z满足的方程通常可以写成λh=f(z)的形式. 若要使误差不会随积分迭代过程呈指数增长, 则必须保证误差传递系数z的模小于等于1, 因此若要使数值方法稳定,λh的取值必须满足: 所有可以使方程成立的z必须全部位于复平面的单位圆内或圆上. 而在实际操作时, 仅需将λh表达为z的函数, 然后让z的取值在单位圆上沿一定方向行进一周并将对应的λh函数值绘制在复平面上即可得到一条闭合曲线, 称为根轨迹线(root lotus), 该曲线围成的内部区域即称为该方法的稳定区间[22]. 通过绘制根轨迹线的方式可以解决大多数用于求解一阶微分方程的数值算法稳定区间的计算, 但用于求解二阶微分方程的数值方法很难通过该方法得出其稳定区间, 如Cowell方法. 对于此类方法稳定区间的计算通常需要借用一些特殊的方式[20,23], 或采用数值实验的方法来确定其最大可选步长的模糊边界.

除此之外, 李雅普诺夫稳定性也是能够造成误差膨胀现象的一个重要原因. 黄天衣等[20]在研究Cowell方法稳定性时, 发现当步长趋于零时并不是所有z的根都会趋于零, 存在部分根会趋于实数1,这一现象与开普勒轨道的李雅普诺夫不稳定性有关, 因此可以将这一部分根视为用于描述李雅普诺夫不稳定性相关的误差传递系数. 由于李雅普诺夫不稳定性所导致的误差膨胀是难以避免的, 且随着积分过程中的误差积累这一影响会越来越显著.

由于此类误差的增长速率远大于其他误差, 故当此类误差单步增量达到与全局误差的单步增量相近的水平之后, 数值解将迅速失真并失去参考价值. 通常情况下, 在发生严重的误差膨胀之后继续对全局误差进行估计将失去实际意义, 因此本文暂不对此类误差进行深入讨论.

2.3 误差分类中的常见争议

由于误差分类是一个开放性问题, 基于不同分类思想所得到的误差其性质也不尽相同, 因此对于一些误差在概念上存在争议是非常正常的, 其中最具代表性的即是关于舍入误差的定义.

狭义上讲舍入误差仅指在某个单一计算步骤中由于解的舍入所产生的误差. 但由于在绝大多数运算中, 各计算步骤所产生的舍入误差并不是简单相加, 而是会经历一系列复杂的误差传递过程, 因此舍入误差与误差传递过程通常是密不可分的, 这就导致了部分人在误差分类时将误差传递过程中所产生的误差同样归为舍入误差的范畴. 这样的分类思想虽然并非没有道理, 但当用于迭代的计算过程时, 由于每一步迭代从上一步中所继承来的旧误差均可被视为这一步的初始误差, 因此如果不将旧误差在计算过程中所产生的误差增加部分与新产生的误差进行区分, 则会对误差分析过程带来极大的困难. 基于这一观点, 这一误差分类思想并不适合用于数值积分过程的误差分析. 而基于这种定义所得到的舍入误差与本文所给出的舍入误差必然会具有截然不同的积累速度.

另外, 还有人会在误差分析时认为, 当截断误差远小于舍入误差时截断误差会被舍入误差淹没,因此在这种情况下仅需考虑舍入误差而不需考虑截断误差. 但事实上, 当截断误差被纳入舍入误差中时, 舍入误差的分布函数会从无偏分布变为有偏分布, 此时若继续将其视为无偏分布进行处理则会导致期望值偏离. 因此这种观点也是不利于误差分析的.

因此, 此处有必要强调一点: 在本文后续分析中所提到的所有误差概念均是基于本节所给的定义, 因此在将本文结论与其他相关结论进行对比时需额外注意误差定义是否一致.

3 数值算例

当不考虑初始误差影响时, 计算误差主要来源于舍入误差、截断误差以及误差传递过程. 由于误差传递过程中次生误差的生成机制与另外两种误差有很大不同, 且其在每一步计算过程中的生成量都十分依赖已有误差, 因此若想对积分过程中的次生误差生成量进行研究, 则需先深入研究舍入误差与截断误差的生成规律. 本文数值实验的主要目的即对以上两类误差的生成与积累的一般规律进行研究, 并验证通过所得规律对全局误差进行估计的可行性.

由于绝大多数需要进行长期积分的天体轨道是周期性或准周期性的, 所以积分过程中所产生的截断误差也会具有一定的周期性, 故截断误差通常可以分解为周期项与长期项两大部分, 其中具有长期积累效应的通常仅有长期项. 因此在进行截断误差生成规律的研究时, 能够较为轻松地将其中的长期项与周期项进行分离是非常重要的. 从这一角度来看, 二体问题是用于进行此项研究的最佳选项.由于本文实验的主要目的仅为对误差估计方法的可行性进行验证, 因此本文并没有选择更为复杂的天体系统模型进行实验, 关于这部分内容我们将在未来研究该方法的具体适用条件的工作中再进行更为细致的讨论.

在关于数值方法的选择上面, 原则上任何拥有固定的计算流程且具有确定的局部截断误差表达式的定步长数值积分方法均可用于本实验. 其中,要求固定的计算流程是为了保证各步的舍入误差增量都能服从同一分布, 而要求具有确定的截断误差表达式则是为了保证每一步的截断误差增量的变化服从固定规律. 此处我们所选的积分方法为精密历表计算中常用的Adams-Cowell PECE3由于通常隐式方法比显式方法精度更高, 因此通常在计算时会使用显式方法给出坐标预报值后再使用隐式方法进行修正. PE即指预报过程,CE即指修正过程, PECE即指每步计算进行一次预报与一次修正.方法[2].

因此, 本文通过使用不同阶Adams-Cowell PECE方法对二维空间中的一组特殊二体系统采取不同步长进行积分来对舍入误差与截断误差的各自规律进行研究, 该二体系统由一个坐标固定不变的有质量天体与一个围绕该天体做匀速圆周运动的无质量天体组成. 由于线性多步法的性能与具体所采用的计算公式有关, 因此在对比几种常见计算公式的舍入误差表现后, 我们最终采用了使用差分格式表达右函数的计算公式参与运算. 以yn、分别表示第n个积分节点处的直角坐标位置、速度以及加速度, 另引入向后差分算子∇, 一阶向后差分的定义为:∇yn+1=yn+1-yn,j阶向后差分的定义为:∇jyn+1=∇j-1yn+1-∇j-1yn. 若使用k步Adams-Cowell PECE方法进行计算, 则本文实验所采用的具体计算公式如下所示:

预报公式(PE)

其中

改正公式(CE)

其中

4 舍入误差分布随时间的变化规律及其对步长的依赖关系

舍入误差的产生是普遍存在于数值运算过程中且是不可避免的. 对于轨道形状较为稳定的周期性或准周期性天体运动过程而言, 若以其每个公转周期为一个积分周期, 则可以近似认为其每个积分周期内的舍入误差积累量服从同一分布. 1917年,Schlesinger[18]在其文章中证明了大量舍入误差之和的概率密度函数趋于高斯分布, 因此可以假定舍入误差的单周期积累量的概率密度服从正态分布.

早在1899年Newcomb[17]就已经指出, 大量舍入误差之和的标准差随样本数增长的速率与求和或积分的次数有关, 在一次求和或积分的情形下,舍入误差积累量的标准差与积分步数n(亦即独立的舍入误差样本数)的关系为, 而在二次求和或积分的情形下则为. Brouwer[19]则在此基础上对舍入误差在天体轨道计算中的积累规律进行了进一步的研究. 根据上述研究的结论, 当使用具有确定计算流程的数值方法计算天体轨道时, 在积分步长给定的情况下, 舍入误差积累量的标准差随时间的增长对于速度计算值而言呈关系, 而对于坐标计算值则呈关系. 因此, 只要能对任意时刻坐标与速度的舍入误差积累量的标准差σ进行测定, 即可对任意时刻坐标与速度计算值的舍入误差积累量的概率密度函数进行估计.

将选择积分步长h积分至t时刻时的舍入误差积累量的概率密度函数记为R(t,h). 由于前面已经讨论过, 在实际计算中, 当步长与初始值确定时,积分到确定时刻的舍入误差积累量并非是随机值,而是确定值[1], 因此, 无法通过重复实验的方法获得其他独立样本, 进而无法通过统计方法研究积分至该时刻时的舍入误差积累量的概率密度函数R(t,h)的标准差. 虽然在步长确定的情况下, 积分至确定时刻的舍入误差积累量为确定值, 但当选取不同积分步长时, 积分至同一时刻的舍入误差积累量则具有一定的随机性. 当选择积分步长为h时, 确定时刻的舍入误差积累量概率密度函数的标准差σt,h随积分步长h的变化规律呈ha, 若引入新变量t=R(t,h)/ha, 则t应与h的选择无关, 即当h选择不同值时的t服从同一分布. 图1即是当舍入误差在全局误差中占主导地位时, 使用不同k步Adams-Cowell方法计算圆轨道问题积分至1000周期时t的概率密度函数直方图与拟合所得的标准正态分布图.

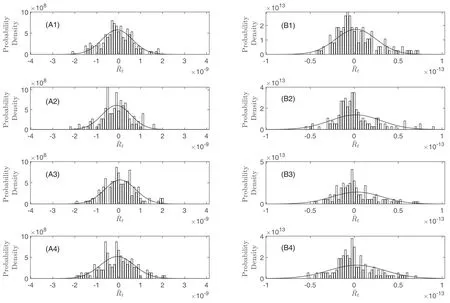
图1 当舍入误差在全局误差中占主导地位时使用不同k步Adams-Cowell方法计算圆轨道问题积分至1000周期时t的概率密度函数. 其中A1(B1)、A2 (B2)、A3 (B3)、A4 (B4)分别对应使用12、13、14、15步Cowell (Adams)方法时的情况. 结果显示, 使用Adams-Cowell方法计算天体轨道时, t大致服从高斯分布, 因此可以使用当选择不同步长时所得的t值进行统计分析, 从而得出舍入误差在任意时刻任意步长时所满足的概率密度函数.Fig.1 The probability density function of t at loop 1000, which is calculated by using different k-step Adams-Cowell method with different k when the rounding offerrors dominate. A1 (B1), A2 (B2), A3 (B3), A4 (B4) represent the cases by using the 12,13, 14, 15 step Cowell (Adams) method. The results show that when the Adams-Cowell method is used to calculate the orbits of celestial bodies, t roughly follows the Gaussian distribution, so the value of t obtained from different time-steps can be used to obtain the probability density function of the rounding error for any time-steps at any epoch.

下面对a的取值进行讨论. 对于一次积分的问题(即求解一阶微分方程)而言, 由于在单步计算中生成舍入误差的取值范围与该步计算结果大小呈正相关, 因此当步长减小一半时, 单步计算所产生的局部舍入误差的可能范围也会减小一半. 若周期误差积累量在原始情况下的概率密度函数方差为σ2, 当步长减小一半时, 假设每个周期积分步数不变(即每隔一步计算一次舍入误差), 则此时σ应为之前的一半, 即此周期误差积累量的概率密度函数的方差为. 但由于步长减小一半时会使每周期步数增加一倍, 即步长减小一半, 此时的实际概率密度函数可以近似视为两个服从同一确定分布却又彼此相互独立分布函数的叠加, 故此时单周期舍入误差积累量的分布函数的方差为, 即σ与成正比, 因此我们可以得出对于一次积分问题,a等于.

为验证这一结论的准确性, 我们设计了两组基于蒙特卡罗方法的模拟实验, 以研究一次积分的舍入误差积累量对步长选择的依赖关系. 实验分别对sintdt两个积分问题在选择步长h分别为π/50、π/100、π/200、π/400、π/800、π/1600、π/3200、π/6400、π/12800、π/25600时

的情况进行模拟, 并假设每步所产生的舍入误差是与单步增量相关且期望为0的均匀随机数, 每组实验各重复10000次进行统计分析, 将其标准差记为σh. 由于二次积分问题(即求解二阶微分方程)的误差增长过程较为复杂, 因此我们选择直接使用蒙特卡罗实验来获取二次积分的舍入误差积累量对步长选择的依赖关系. 对于此问题我们同样设计了两组实验, 分别以dtdt与sintdtdt两个积分问题为例对σh与h之间的依赖关系进行研究, 参数沿用与上一组实验相同的设定. 实验结果如图2所示, 结果表明对于一次积分问题而言, 舍入误差积累量分布函数的标准差与成正比, 即此时a等于, 而对于二次积分问题而言, 舍入误差积累量分布函数的标准差与h成正比, 即此时a等于.

5 截断误差积累量的增长规律及其对步长的依赖关系

当被积的天体轨道具有明显的周期性时, 其截断误差可分为周期项与长期项两大部分, 其中周期项在局部截断误差中占主导地位, 而长期项所占比重远不及周期项部分.因此在使用Adams-Cowell方法或任何其他数值积分方法计算天体轨道长期解时, 如果仅将目标积分时刻所能容许的最大误差平摊到每一步中, 并以该值与局部截断误差的大小关系作为步长控制的标准, 则通过这种方式所决定的步长必然远远小于其最大可选步长, 这会导致严重的时间与计算资源的浪费. 因此, 对此类轨道问题计算时的长期截断误差积累量的定量或半定量研究具有极其重要的现实意义.

5.1 截断误差长期积累量的增长规律

假设在起始时刻t0时全局误差为0,积分步长为h, 若用yt0+h表示通过数值方法所得的y在t0+h时刻的计算值, 而用y(t0+h)表示y在t0+h时刻的理论值, 则y在t0+h处的局部截断误差(Local Truncation Errors, LTE)可以表示为

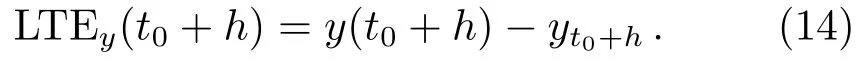
以k步Adams-Cowell CE方法为例进行分析,默认y为D阶向量,D为该轨道所在的构型空间的维度,y′、y′′、y(j)分别为y的一阶、二阶与j阶导数.假如各计算值均与理论值相等时, 计算所得的yt0+h与y′t0+h的局部截断误差则可以表示为

其中cj与mj为积分常数, 具体取值可由同阶的(9)式与(10)式展开获得. 使用泰勒公式将上述两式中的各项在t0处展开, 整理后得到的截断误差表达式为

其中aj=ck+j+1,a*j=mk+j+1.

在实际情况下参与计算的所有y、y′、y′′均为其在各时刻的计算值, 因此实际的局部截断误差还应叠加一个由全局误差的存在引入的修正项. 当步长与方法选择合适时, 理论上可以将整个积分区间内的全局误差控制在较小水平上. 假设存在一个小量ε(0＜ε ≪1), 若可以使在整个积分区间内该修正项与主项的数值大小之比一致小于ε时, 则该修正项所造成的影响可视为关于ε的一阶小量, 因此在仅做定性或半定量分析时可忽略该项的影响.

对于周期函数而言, 其截断误差一般可分为周期项与长期项两部分, 一般情况下当积分时间足够长时, 截断误差的长期项在其总积累量中占主要地位, 故此处仅对其长期项进行研究.

当使用k步Adams方法计算天体速度时, 若记其积分起始时刻为0, 单周期积分步长数为m, 对应的所选积分步长为h, 则其单周期截断误差积累量可以记为

理想情况下, 由于y为周期函数, 因此单周期截断误差积累量中ε的0阶项与起始位置无关. 若记

则其n个周期截断误差积累量可以写为

由于截断误差的周期项不具备长期累积效应,因此当n足够大时可认为Adams方法的截断误差的积累量与时间的关系大致呈一次函数, 即对于一阶微分方程的数值求解过程而言, 截断误差的积累量与时间t成正比.

对于Cowell方法而言, 由于

故其截断误差并不直接积累到y中而是直接积累在∇y中, 因此对于k步Cowell方法而言, 若令

则∇y中的单周期截断误差积累量表达式应具有以下形式

而y中的单周期截断误差积累量表达式应有以下形式

则其原函数在第n个周期结束时的截断误差积累量应为

当n趋于无穷大时

即当使用k步Cowell方法计算天体坐标时的截断误差积累量随时间的增长曲线会随积分过程所完成的周期数的增加而逐渐趋于二次曲线, 即对于二阶微分方程的数值求解过程而言, 截断误差积累量增长速率近似与t2成正比.

图3为以单周期步长数为40步时使用不同k步Adams-Cowell方法对圆轨道进行计算时所产生的误差积累情况. 此时由于步长选择较大, 因而截断误差在全局误差中占据主导地位. 结果表明, 截断误差的增长规律符合上述结论.

图3 当截断误差在全局误差中占主导地位时使用不同k步Adams-Cowell方法计算圆轨道问题的相对全局误差随积分周期数的增长关系图. 可见当使用Cowell方法计算天体位置坐标时截断误差与t2成正比, 而使用Adams方法计算速度时的截断误差增长为线性(单周期步长数=40).Fig.3 The accumulation speed of globle error proportional, which is calculated by k step Adams-Cowell method with different k when the truncation errors dominate. It shows that the accumulation rate of the total truncation errors for the position calculating of celestial bodies with Cowell method is related to t2. For the velocity calculating with Adams method, the total truncation error increases linearly (40 steps per loop).

由于一次积分方法与二次积分方法的舍入误差的标准差的增长速率分别仅有与, 因此对于两种方法而言, 其截断误差的增长速度相较于舍入误差更快. 故无论步长选取多小, 只要当积分时间足够长时, 截断误差的影响必然最终超越舍入误差4此结论仅当舍入误差与截断误差定义与本文所给定义一致时成立, 若所给出的舍入误差包含误差传递则不成立..

图4为选择12步Adams-Cowell方法对圆轨道进行积分时, 积分至不同周期数时的全局误差随单周期步长数的变化曲线. 由于截断误差与舍入误差的性质区别, 其对步长变化相应也具有不同特征. 截断误差随步长变化的曲线应为光滑的单调曲线, 而舍入误差随步长变化的曲线则应表现为无规则的随机涨落, 因此可通过这一特征来判断当选择某一步长时哪一类误差占据主要地位. 结果表示, 随着积分周期数的增加, 截断误差占主导的步长区间将逐渐扩大, 舍入误差占主导的步长区间则会相应缩小. 该结果充分说明了上述判断的正确性.

图4 当使用12步Adams-Cowell方法计算圆轨道问题的相对全局误差的常用对数在不同积分时刻处随步长选择的变化关系图. 图中曲线形状较为规则的区域即为截断误差主导的区间, 而曲线形状呈无规则的随机涨落形态的区域即为舍入误差主导区域. 可见随着积分时刻的推移截断误差主导的区域会逐渐扩大, 即截断误差积累量的增长速度较舍入误差更快.Fig.4 The time-step dependence of globle error proportional’s Briggs logarithm, which is calculated by 12 step Adams-Cowell method for circular orbit problem. The region where the curve shows the feature of irregular fluctuations is dominated by rounding offerrors, otherwise is dominated by truncation errors. As is shown above, the region dominated by the truncation errors will invade the region dominated by rounding offerrors gradually as the time goes on, which means that the accumulation rate of the truncation error is higher than the rounding error.

5.2 截断误差积累量对步长的依赖关系及其在截断误差积累量估计中的应用

根据数值积分的欧拉法公式

其中R(h2)为欧拉法公式的局部截断误差, 其表达式可以通过使用泰勒展开式与欧拉法公式相减的方法获得, 可表示为

当积分m步之后

若记

则(30)式可展开为

其中dj与h无关.

对于确定轨道而言, 在初始时刻t与积分步长h都确定时, 则当积分进行至t+ Δt时刻时的值是唯一确定的, 且其值仅与h的选择有关, 因此我们可以将其表示为如下的级数形式

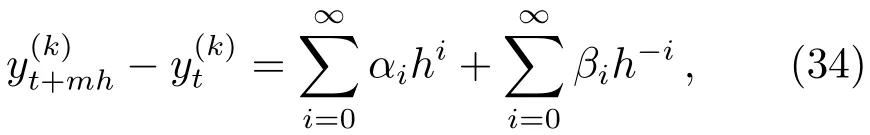
其中αi与βi均与h无关. 若用y(k)(t)表示y(k)在t时刻的真实值, 则当h趋于0时

因此

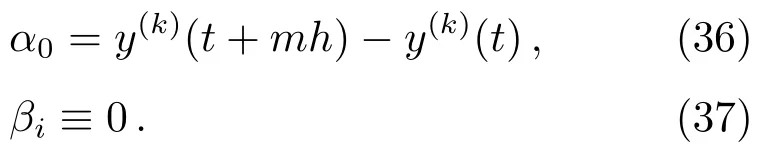
将(36)式和(37)式代回(34)式, 即有

对于一般轨道而言,C*j与Cj难以通过解析方法得到, 因此更加可行的方法是对该曲线进行拟合(如使用最小二乘法). 虽然在全局误差中同时包含截断误差与舍入误差两部分, 但由于截断误差对积分步长的敏感程度远大于舍入误差, 因此当积分时间足够长时, 总是可以找到足够宽的步长区间使得该区间内的截断误差远大于舍入误差, 如此即可认为此时的截断误差积累量约等于全局误差.

由于一般情况下用于拟合的数据点对应的积分时间跨度总是远小于实际计算时的目标积分时间跨度, 且截断误差积累量的增长速率比舍入误差积累量快, 若要使最终的截断误差积累量控制在与舍入误差积累量相近的水平, 则用于拟合的数据点所对应的积分步长的大小必须远大于实际计算时所选择的积分步长大小. 由于截断误差积累量的表达式中h的高阶项会随h的减小而快速收敛, 因此在实际情况下仅需截取该表达式的前有限项即可对最终的截断误差积累量进行较为准确的估计.

需注意的是, 在进行数据拟合时并不是保留项数越多估计得越精准. 由于在所选区间的步长较小一端不可避免地会有许多数据点中包含很大比例的舍入误差信息而呈现一定程度上的随机性涨落,而当保留项数过多时可能会导致在拟合时将舍入误差所导致的数值涨落一并考虑在内从而导致严重错误, 因此一般仅保留前4–6项即可. 除此之外,如果用于进行数据拟合的步长区间选择不当同样也会使估计结果产生严重偏离, 在实际操作时可以在确定步长区间之后选择不同项数分别进行拟合,当步长区间选择合理时总会有多条曲线在步长较小端收敛到同一曲线附近, 否则即表示步长区间选择不合理, 则应重新选择合理的步长区间.

若将在t1时刻取y的误差多项式前s项拟合所得表达式的函数记为Ty,s(t1,h), 则在理想情况下, 当选取不同的前s项进行拟合时(暂记为s1与s2), 应有

其中δ为所能允许的截断误差估计值的相对误差量级.

若通过拟合所得的各表达式中有多个表达式间相互关系满足上式, 则满足该关系的所有表达式均可以用来对截断误差积累量进行估计. 当拟合结果较好时, 不同拟合结果间的相对误差应至少小于1, 此时对应的δ等于0. 因此, 若所得的所有曲线右端发散或趋于非负数值, 则说明所选区间不合理, 即无法确保此时所得的所有误差估计公式的可靠性.

图5为使用10步Adams-Cowell方法计算圆轨道, 并以[24,83]为用于拟合截断误差表达式的单周期步长数采样区间时, 保留不同前s项和所得出的误差估计曲线之间的对比. 需注意, 坐标误差拟合的最佳步长区间与速度误差拟合的最佳步长区间不尽相同, 因此应各自判断, 否则会使δ过大, 影响误差预测精度, 如图5所示.

需要额外注意的是, 以上误差估计方法虽然是基于Adams-Cowell方法得出, 但实际上其原理与Adams-Cowell方法并没有必然联系, 理论上对于任何具有确定局部误差表达式的数值积分方法均适用.

5.3 对未知积分器截断误差积累量进行估计

在使用数值积分方法计算天体轨道时, 可供选择的积分方案往往不止一种. 以线性多步法为例,在进行积分器设计或选择时往往有不止一种可选方案, 如由p阶预报公式与p阶改正公式组成的p阶PECE方法, 又如由k步预报公式与k步改正公式组成的k步PECE方法5需注意, 对于线性多步法而言, k阶方法与k步方法是两个截然不同的概念. 如对于Adams方法而言, k步预报公式为k阶, k步改正公式为k+1阶[4]., 又如在p阶Adams-Cowell PECE方法基础上结合外推法进行修正的方法[25–26], 又如KSG积分器[10–11]以及由于具有保辛特性因而在长期数值积分中具有潜在优势的对称多步法(Symmetric multistep method)[27]等. 同样, 对于常用于长期轨道演化研究的MVS型辛方法而言, 可供选择的具体积分器也有许多, 如ABA(H)82、ABA (H)84、ABA (H)104、ABA (H)864和ABA (H)1064等6此类积分方法在不同文章里提及时所使用的名称不尽相同, 如MVS方法、WH积分器(Wisdom-Hoffman integrator)[28-29]、PSI(Pseudo-high-order Symplectic Integrator)积分器[30]、Lie-Poison积分器[31]、“leap frog”方法[7-8]等. 而对于基于此类方法的具体积分器的命名方式也各不相同, 本文所采用的是Blanes等[12]与Farr´es等[13]所采用的命名方案, 关于本文中所提及的各种具体积分器的详细资料、出处及适用条件见文献[12–13]. 此外, 关于此类积分器的家族极其庞大, 除了Blanes等[12]所提到的一系列积分器之外还有许多具有其他性能特征的积分器, 关于此类积分器的更加细致的介绍见文献[14]..

在当前的大多数情况下, 人们在进行积分方案选择时通常会以满足实验精度需求为主要目的, 而并不会对性能提出过高要求. 这一方面是由于积分方案的性能对比研究是一项计算量极其庞大的工作, 需要进行大量的数值实验研究, 而此过程所需付出的时间成本与所得实际收益之间是严重不成正比的. 另一方面, 因为积分器选择的主要考量因素之一是其截断误差, 而当积分器精度较高时其截断误差增长会变得极其缓慢, 从而使得难以通过数值实验来获取其截断误差性能, 因此性能越好的算法往往越难对其截断误差性能进行检测, 而这极大阻碍了对极致性能的追求. 事实上, 如果存在一种方法能够使用已知的积分器实验数据来对性能未知的数值积分器的截断误差积累速率进行推算, 或是使用同类积分器在使用低阶方法时所得的数据对高阶方法的性能进行推算, 则能够极大地缩短对各种不同积分方案进行性能测试所需的时间, 从而使对极致性能的追求成为可能. 因此, 我们在此处以不同阶的n步Adams-Cowell方法为例, 讨论如何通过已知积分器的相关实验数据对未知积分器的截断误差积累量进行估计.

前面我们已经证明对于确定的轨道实例, 当选择确定的步长时, 在确定时刻其截断误差积累量的长期项具有确定的表达式, 如(39)式和(40)式所示. 对于不同积分器而言, 其所对应的系数也不尽相同, 而使用已知积分器数据对未知积分器进行截断误差积累量(长期项)估计本质上就是使用已知积分器的各项系数对未知积分器的对应系数进行近似求解. 而由于对于步长较小时截断误差积累量表达式中各项的收敛速度极快, 因此通常仅需考虑其前2–3项, 甚至部分所选步长极小的情况下只需考虑首项即可对截断误差积累量实现较为准确的估计. 因此, 理论上在任意积分时刻选择任意步长时,只要能够给出使用各种积分器所产生的截断误差积累量之间的关系, 即可实现对未知积分器的截断误差积累量估计.

以k取不同值时的Adams-Cowell方法为例, 如图6所示, 若以Tk(t,h)表示在选择时间t与步长h时使用k步Adams-Cowell方法所测得的截断误差积累量相对值, 则根据所得数值可以发现, 在满足数值稳定性的前提下, 使用此类方法所产生截断误差积累量大致满足以下关系

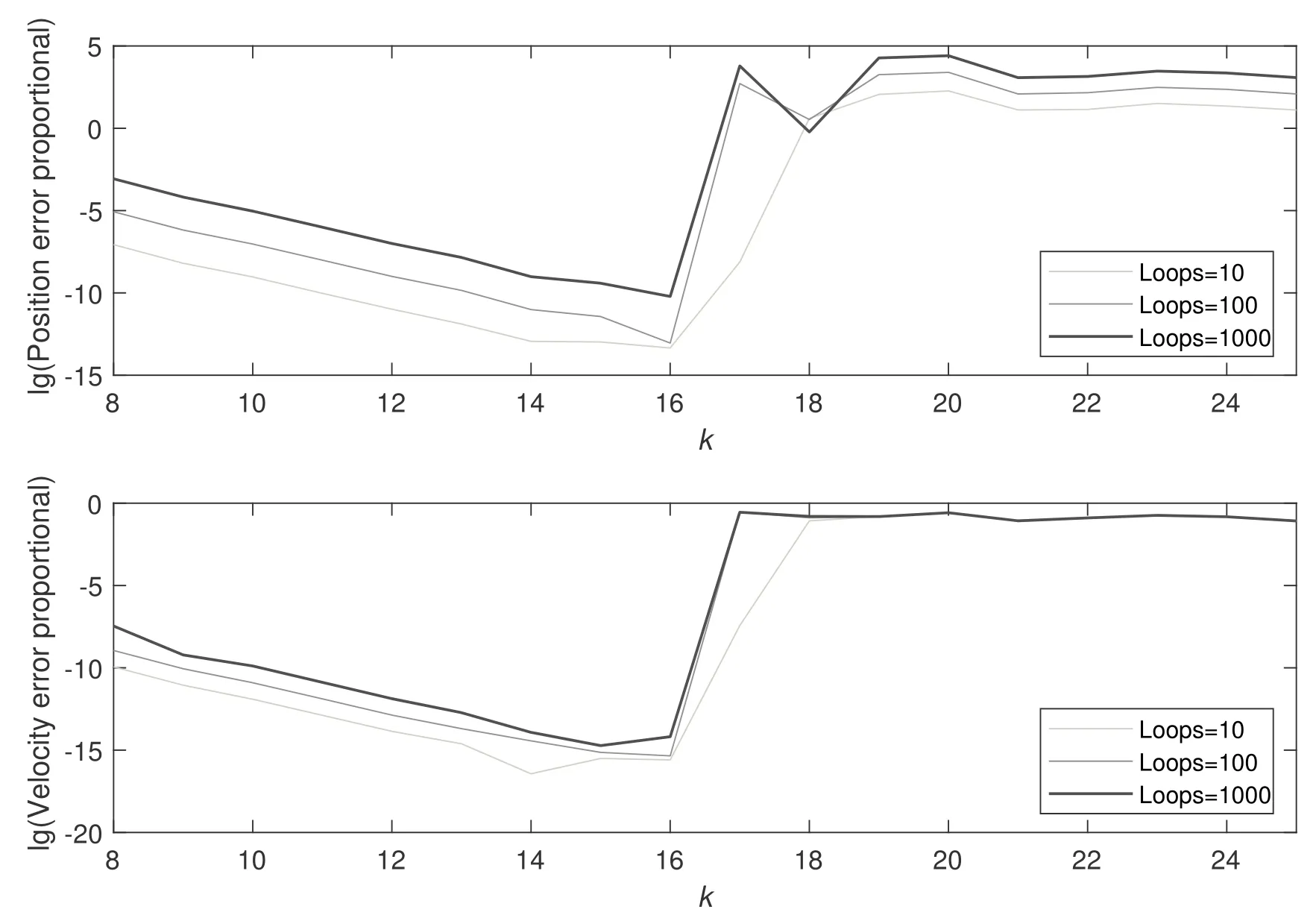
图6 k步Adams-Cowell方法计算圆轨道问题的相对全局误差的常用对数对k的依赖关系(单周期步长数=50). 图中骤变处即表示跨越了稳定区间边界, 因此可以在遍历不同单周期步长数时的曲线突变位置的变化来确定不同k值时所对应的稳定区间范围.Fig.6 Briggs logarithm of globle error proportional at different k when calculating circular orbit while using k step Adams-Cowell method (50 steps per loop). The sudden change in the figure indicates that the boundary of the stability zone has been crossed, so that the step count per loop dependence of the sudden change point can be used for the stability zone determination for different k.

图7为基于上式所得规律使用了10步与11步Adams-Cowell PECE方 法 对12步Adams-Cowell PECE方法的计算误差进行估计的实验. 结果显示实测误差全部落在基于该规律所建立的误差估计理论所给出的99.6%置信区间之内, 充分说明了该误差估计理论的可行性.

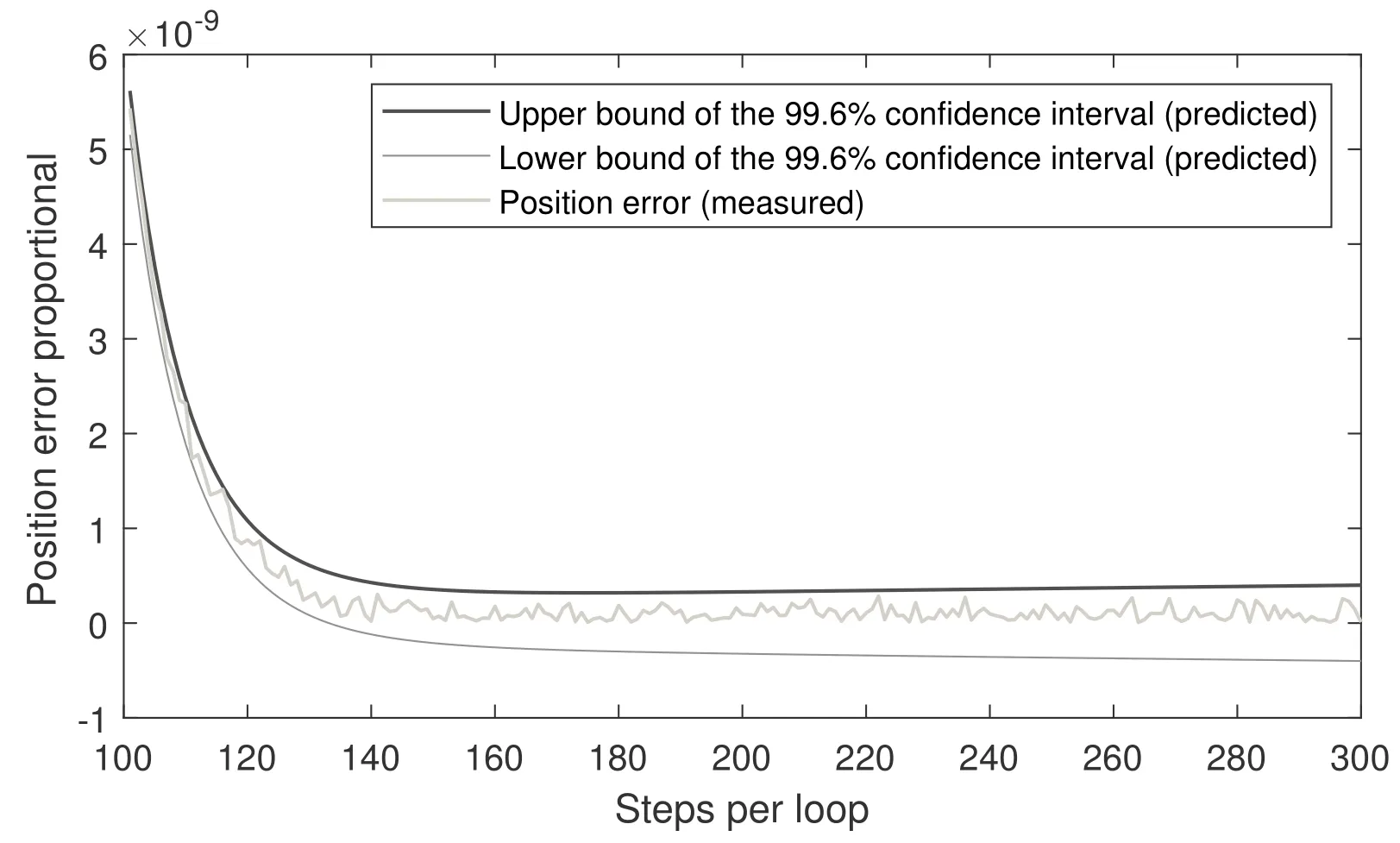
图7 误差估计方法的可行性测试. 用10步与11步Adams-Cowell方法在第100周期处的信息对12步方法对第1000周期的坐标误差进行估计. 上下两条曲线分别为估算得出的99.6%置信区间边界, 中间的曲线为此处全局误差的实测值. 结果显示该方法估计效果十分理想.Fig.7 Feasibility test for the error estimation method. Estimate the position error of 12 step Adams-Cowell method at loop 1000 method by using the information of 10 and 11 step Adams-Cowell method at loop 100. The upper and lower curves show the boundary of the estimated 99.6% confidence interval, and curve in the middle is the measured values of global errors. The result shows that our method is quite reliable.

这一超越积分器界限的截断误差积累量估计方法对于在解决实际问题时的方法选择具有非常重要的指导意义, 尤其是在对积分方法进行选阶时的帮助尤为关键. 由于数值积分方法的阶数越高截断误差越小, 因此当用于进行数值实验的积分时间跨度确定时, 可用于进行截断误差积累量表达式拟合的步长区间的下界会随阶数升高而增大. 故若要对使用此条件下的截断误差积累量进行直接测量,则所需的计算量将是十分庞大的, 且由于所需的积分时间较长, 此过程中所需面对的舍入误差的影响也将极为显著. 基于这一原因, 在对高阶方法的截断误差积累量进行研究时, 使用先前所给出的直接测量方法基本难以奏效, 这也就充分体现了这一跨积分器界限的截断积累量误差估计方法的重要性.

需要额外注意的是, 此跨积分器界限的截断误差积累量估计方法的应用条件为所涉及的积分器的截断误差积累量表达式必须满足(39)式和(40)式的形式, 即对于确定轨道计算实例, 截断误差积累量长期项的表达式必须只能与时间和步长有关. 因此, 在将此方法应用于MVS方法时需要额外注意控制时间和步长之外的其他影响因素.

6 总结与展望

数值积分方法的误差增长规律研究对于数值积分方法的应用而言具有重要参考价值. 当不考虑初始误差且所选步长可使积分算法满足稳定性条件时, 若想实现对选取任意步长进行长期积分时所产生的误差总量进行较为准确的估计, 则需充分了解该过程中产生的总舍入误差分布函数与截断误差积累量随时间与步长变化的规律以及该系统各个维度上的平均误差传递系数. 其中, 当误差膨胀的影响开始变得显著之后, 系统往往会快速失真从而失去继续研究的价值. 因此在一般情况下, 仅需了解舍入误差与截断误差的生成规律即可实现对绝大多数实际轨道的误差估计, 本文即主要针对这一问题. 具体规律如表1所示.

表1 直角坐标系下舍入误差标准差与截断误差积累量的变化规律Table 1 Variation of standard deviation of rounding error distribution and total truncation error in Cartesian coordinates

基于以上规律, 我们提出了一种简单高效的误差估计方法, 并用实验证明了该方法理论上的可行性. 该方法仅需进行较少数值实验即可对任意步长、积分至任意时刻、使用任意积分器时所产生的舍入误差分布函数和截断误差积累量进行估计,且理论上可以适用于任意具有确定局部截断误差的表达式和固定计算流程的数值方法. 同时, 该方法也可用于轨道周期性显著且误差膨胀不显著情况下的天体轨道长期数值解的全局误差估计, 这也是首个可以从概率分布角度对数值方法的舍入误差进行定量研究的方法.

该方法目前虽已经能够很好地满足绝大多数积分方法的性能研究与对比工作, 但在用于一般轨道全局误差估计时的适用条件仍有待进一步研究.这是由于在绝大多数情况下截断误差积累量的长期项都难以彻底剥离出来, 而目前所给出的截断误差估算方案须高度依赖于截断误差积累量长期项可分离的基本假设. 因此, 在使用该方法估计截断误差积累量的变化趋势时, 需要充分考虑截断误差周期项残余所带来的影响. 而关于如何消除这一影响, 或如何对这一影响所可能造成的误差估计值的偏移量进行定量评估, 则需要开展进一步的研究才能得出结论.

虽然目前基于上述理论的误差估计方法在适用范围上仍存在局限性, 但已经表现出了巨大的发展潜力. 随着研究的进一步深入, 该方法将有望成为天体轨道计算领域中的一项重要辅助工具–不仅可以作为一种精准高效的轨道数值积分误差分析方法, 同时也能为长期轨道积分任务中的积分器选择与具体积分方案设计提供重要帮助.

致谢 感谢审稿人对文章提出的宝贵建议, 使得文章的质量有了显著的提高.