柔性直流系统短路故障网络阻抗建模与时频特性诊断方法研究
蒋佳丽,刘毅敏,王朋
(武汉科技大学 信息科学与工程学院, 武汉 430081)
0 引 言
柔性直流系统直流侧发生短路故障后,故障电流快速上升,在数毫秒之内危及整个电网,必须快速切除故障线路以保证系统的安全可靠运行。然而,如何实现快速准确的故障线路识别仍是一个难题。为降低线路故障率,直流线路多采用电力电缆,电缆故障多为永久性故障,需停电检修、离线诊断并及时恢复。相比而言,采用架空线路更具有经济性,但其故障概率较高,易发生暂时性故障,降低了直流线路可用率和供电可靠性,其对直流线路故障诊断的准确性提出了更高要求[1]。
传统过流、欠压保护不具备选择性,距离保护则由于难以在数毫秒内精确测距而无法满足直流电网的速动性要求[2]。柔性直流系统中电容分布在MMC换流器子模块中,发生单极接地故障的瞬态故障电流并不明显,存在难以被检测导致电流差动保护无法可靠动作的问题[3],高度依赖于高速通信数据同步。常规直流输电系统以行波保护作为线路主保护具有一定的借鉴意义[4],但存在行波波头较难识别和对采样率要求较高等问题[5],在多分支线路的多端或环形网络尤为明显。
从主动构造故障特性信号的角度,文献[6]提出了一种向故障回路直流侧投入一个带初始电压的电容,根据特征频率分析得到故障距离的方法。文献[7]提出的“握手法”,采用先跳后合的方案,无需通信即可实现直流环网故障线路的识别与隔离,这种方案速动性较差,而且可能短时断开非故障线路。由于直流系统不存在正负零序分量,交流系统中基于零序分量的方法不再适用,但基于线路参数的故障识别和保护方法仍可以用于线路故障定位,如:基于阻抗辨识[8]和参数识别原理[9]等。
在故障信号分析和特征识别方面,文献[10]利用少量能表征实际故障电流行波的小波变换模极大值进行数据交互,缓解了线路两端高速采样数据实时性对差动保护的影响。文献[11]根据区内、外暂态信号的局部高频和低频频段的比值作为故障诊断判据,文献[12]采用小波变换和相模变换分析故障电流提高故障识别率。这些方法在内故障的情况下,所含故障暂态信息不充分、可能导致误判故障。目前大多数研究者运用小波变换提取故障时域和频域信息,在时域或频域里作相关性分析进行线路保护[13-15]。文献[14]行波波形特征的时频相关性和差异性,提出了单端行波保护和故障定位方法,有效克服了局部信息导致保护可靠性不高的缺陷。
直流侧线路短路故障必定引起网络阻抗变化,为此提出基于阻抗网络暂态响应时频特性关联度的故障诊断方法。该方法利用暂态信号时频变换分析方法可多次重复提取故障网络特征,以与标签样本相匹配为判定依据,能够有效保障检测精度,有助于提高故障诊断的准确性。
文中首先建立基于MMC换流器等效电路和线路分布参数的柔性直流系统精确模型,旨在研究故障网络阻抗的时域响应特性,详细分析了不同故障点经不同大小电阻短路的故障特征。其次,讨论了基于Mexican Hat变换的时频分析方法,用于获取时频能量序列,以构造能量谱矩阵,经模拟仿真和数值计算可建立样本库。然后,通过相似度计算选出与实测故障特征最相近的样本,确定故障点位置和估计短路电阻大小,并优化诊断判据。最后,利用电磁暂态仿真分析,并与多种时域方法相比较,验证了所述方法的可行性和有效性。
1 柔性直线路短路故障网络建模与阻抗特性分析
1.1 柔性直流系统网络阻抗模型
基于MMC换流器的三端柔性直流系统如图1所示,3个换流器直流极由平波电抗器引出,三回线路呈Y型连接,正(负)极汇交于c(d)点。设在e(f)处正负极之间经电阻Rd发生短路,MMC3换流器出口处的测点为a(b)点,则图1中柔直系统网络划分为4个二端口网络(Q1~Q4)和3个阻抗串联支路。其中,Run、Lun、Cun(n=1, 2, 3, 4)分别为单位长度均匀传输线路的零序分布电阻、电感和电容[16];Ldc为平波电抗;MMC的等效模型可局部线性化为由子模块等效电容Cc、桥臂等效电抗Lc和等效电阻Rc串联组成[17-20],可令ZMMCm=1/jwCcm+jwLcm+Rcm(m=1, 2, 3)。
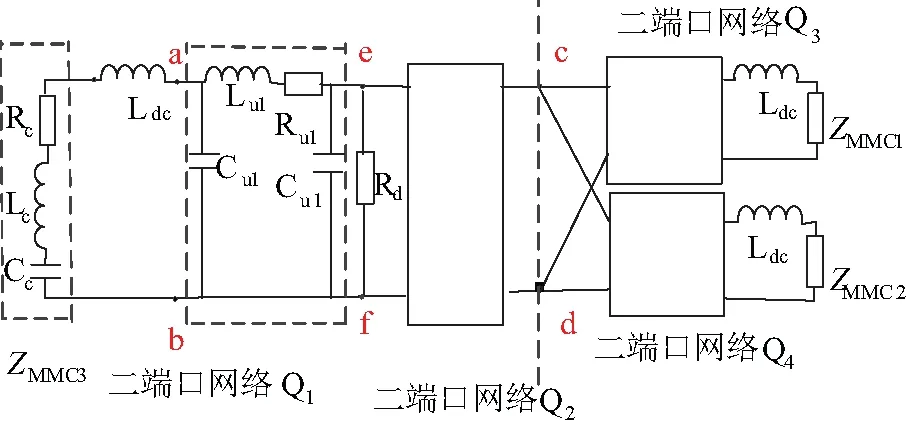
图1 MMC型三端柔性直流系统等效网络
图1中线段cd左侧为级联线路,右侧为并联线路。故障线路段从故障点到换流器直流出口电抗器的输入阻抗可以看成由所有并联线路的输入阻抗并联后再与级联线路串联而成。
测点a(b)右侧两个二端口网络Q3和Q4的入端阻抗Zcd3、Zcd4均可表示为[16]:
(1)
式中m=1, 2, 3;n=1, 2, 3,4;l1~l4为二端口网络Q1~Q4线路长度;Zc为波阻抗;g为传播常数。
由二端口网络传输方程可得传输参数表达式为:
(2)
对于既定二端口网络Q1~ Q4,其线路分布参数和长度均为已知,则由式(2)可得对应传输参数T1~T4。
图1中e(f)处极间故障接地电阻元件可以看作一个二端口网络,其参数矩阵为:
(3)
级联二端口网络传输参数矩阵表达式为
(4)
其中:
式中l1、l2分别为线路交汇点b(c)左侧故障点两侧的线路段长度。
将二端口网络Q3和Q4的入端阻抗看作是故障点e(f)左侧网络的负荷Zcd,则故障线路段从故障点至换流器直流出口电抗器的输入阻抗可表示为:
(5)
由图1中测点a(b)之间的等效阻抗可以看作(ZMMC1+jwLdc)和Zab的并联阻抗,该阻抗的频变特性与故障点位置和电阻大小密切相关,有助于确定故障点位置和估计故障电阻大小。
1.2 短路故障网络阻抗特性分析
为分析故障网络阻抗特性,搭建如图1所示柔性直流系统精确模型,各部分具体参数为:
Rc=3.33 Ω,Lc=64 mH,Cc=180 μF,Ldc=10 mH,Rou=0.014 Ω/km,Lun=0.82 mH/km,Cun=0.001 μF/km,l=l1+l2=600 km,l3=l4=300 km。
模拟不同故障位置经不同大小电阻Rd发生短路故障,在图1模型中,依次向a、b两端注入幅值为500 V、宽度为0.01 ms脉冲电压作为激励,实时提取暂态响应电压分量变化曲线中3 μs~6 μs段,如图2所示。其中,故障点e(f)与测点a(b)的距离为L。
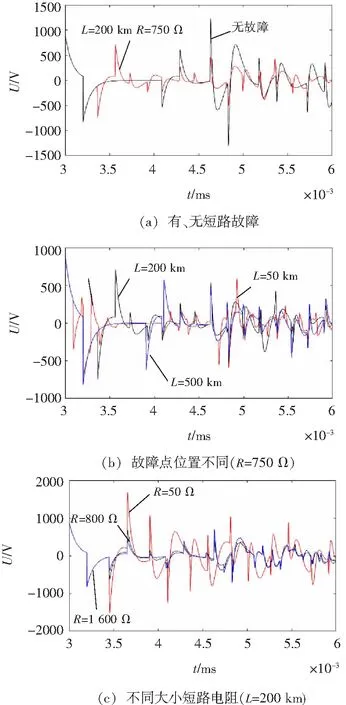
图2 暂态响应电压分量随时间变化的曲线
由图2可得出如下规律:
(1)故障阻抗网络暂态响应时频特性可用于判定是否发生短路故障;同一位置发生短路故障时,暂态响应故障特征曲线与短路电阻大小有关;短路电阻大小相同时,不同位置短路故障所对应暂态响应故障特征曲线也有差异;
(2)图2(c)所示距离测点250 km处经电阻800 Ω和1 600 Ω发生短路的暂态响应故障特征曲线较为相似,此时由于时域特征难以区分,所以可以从频域特征获得更多信息,尤其是零极点附近的局部信息。以图2(c)中距离测点250 km处经电阻800 Ω发生短路的暂态响应故障特征曲线为例,对3 μs~4 μs的曲线段进行Mexican Hat变换,得到如图3所示时频暂态信号,其局部特征相对于时域局部特征而言更丰富,更容易识别。

图3 小波时频特性图
2 故障网络阻抗特性时频域分析方法
在同一激励作用下不同阻抗网络的暂态响应特性有所不同,对暂态响应特性进行时域(或频域)分析能够反映不同阻抗网络的时域(或频域)特性。可以利用相似度衡量不同暂态响应信号波形的相关性,或经时频变换到频域来分析信号的相似度。
2.1 基于累积距离和灰色关联度的相似度计算
2.1.1 动态时间规整与累积距离计算
动态时间规整(Dynamic Time Warping, DTW)是一种衡量两个时间序列之间相似度的方法。对样本暂态电压分量序列Xi和实测暂态电压分量序列Xj,构造一个m×n的矩阵网格,矩阵(i,j)处的元素为Xi和Xj两点的欧氏距离为:
d(Xi,Xj)=(Xi-Xj)2
(6)
可知d(Xi,Xj)越小,则Xi和Xj越相似,该方法可以归结为寻找一条通过此网格中若干格点的路径,其路径计算如下:
D(i,j)=d(Xi,Xj)+min{r(i-1,j-1),r(i-1,j),r(i,j-1)}
(7)
式中D(i,j)为当前格点距离,表示到达该点的最小的邻近元素的累积距离之和,等式右侧各项表示每个格点的三条路径,分别为下、左、斜下。可知累积距离D(i,j)越小,Xi和Xj越相似。
2.1.2 灰色关联分析与关联度计算
灰色关联分析方法(Grey Relation Analysis, GRA)是根据因素之间发展趋势的相似或相异程度(即灰色关联度)来衡量因素间关联程度的一种分析方法。每个暂态响应电压分量变化曲线可以看作离散序列,若每个序列均含有n个元素,则第i个样本暂态电压分量序列可以表示为Xi={xi(1),xi(2), …,xi(k),…,xi(n)) } (k=1,2,…,n),可令实测故障序列为Xj。
如式(8)将Xi的各元素归一化,在各个时刻(即曲线中的各点)样本暂态电压分量序列Xi与实测暂态电压分量序列Xj的关联系数Dij可用式(9)表示:
xi(k)=xi(k)/xi
(8)
Dij=
(9)
式(9)中ξ称为分辨率范围从0~1,通常取0.5。Dij越大,曲线越相似。
2.2 时频变换特征矩阵构建与相似度分析
2.2.1 Mexican Hat变换与时频矩阵构建
对原始的连续暂态电压分量f(t)=xi(k)进行连续小波变换,按t=nTs,b=kTs,对WTf(a,b)求卷积有:
(10)
式中ΔT=Ts是采样的间隔;WTf(a,k)为小波变换系数经过尺度a的伸缩和k的平移之后所得。函数ψ(x)为基小波,可取为Mexican Hat函数如下:
(11)

(12)
(13)
由式(13)可得反映原始信号时-频域特性的时频能谱矩阵Em×n
(14)
2.2.2 时频谱矩阵相似度识别方法
借助图像识别中相似度原理可以刻画两矩阵间的相似性,进而判断矩阵的相似度。假设n(距离检测点x/km)发生故障,在检测点可检测到时频波形,由式(14)可以获得故障时频矩阵Wx,在样本点y(距离检测点y/km的样本时频矩阵为Wy,则这两个故障点的故障行波波形相关性为:
(15)
式中Cov(Wx,Wy)为向量Wx和Wy的协方差矩阵,Cov(Wx,Wx)和Cov(Wy,Wy)分别为向量Wx和Wy的方差。Dxy为一个二维矩阵,Dxy(0,1)为Wx和Wy的相关系数,Dxy(1,0)为Wy和Wx的相关系数,有Dxy(1,0)=Dxy(0,1)。可知相关系数值越大则x与y处的故障特征相近。
3 基于时频分方法的故障诊断流程及判据
所述时频分析方法及其故障诊断步骤如下:
(1)建立如图1所示的柔性直流系统精确模型,模拟不同故障位置经不同大小电阻发生短路故障,注入脉冲电压作为激励,提取暂态响应电压分量并构建样本时域特征库X和时频能量谱矩阵特征库E;
(2)故障特性时频分析及相似度计算
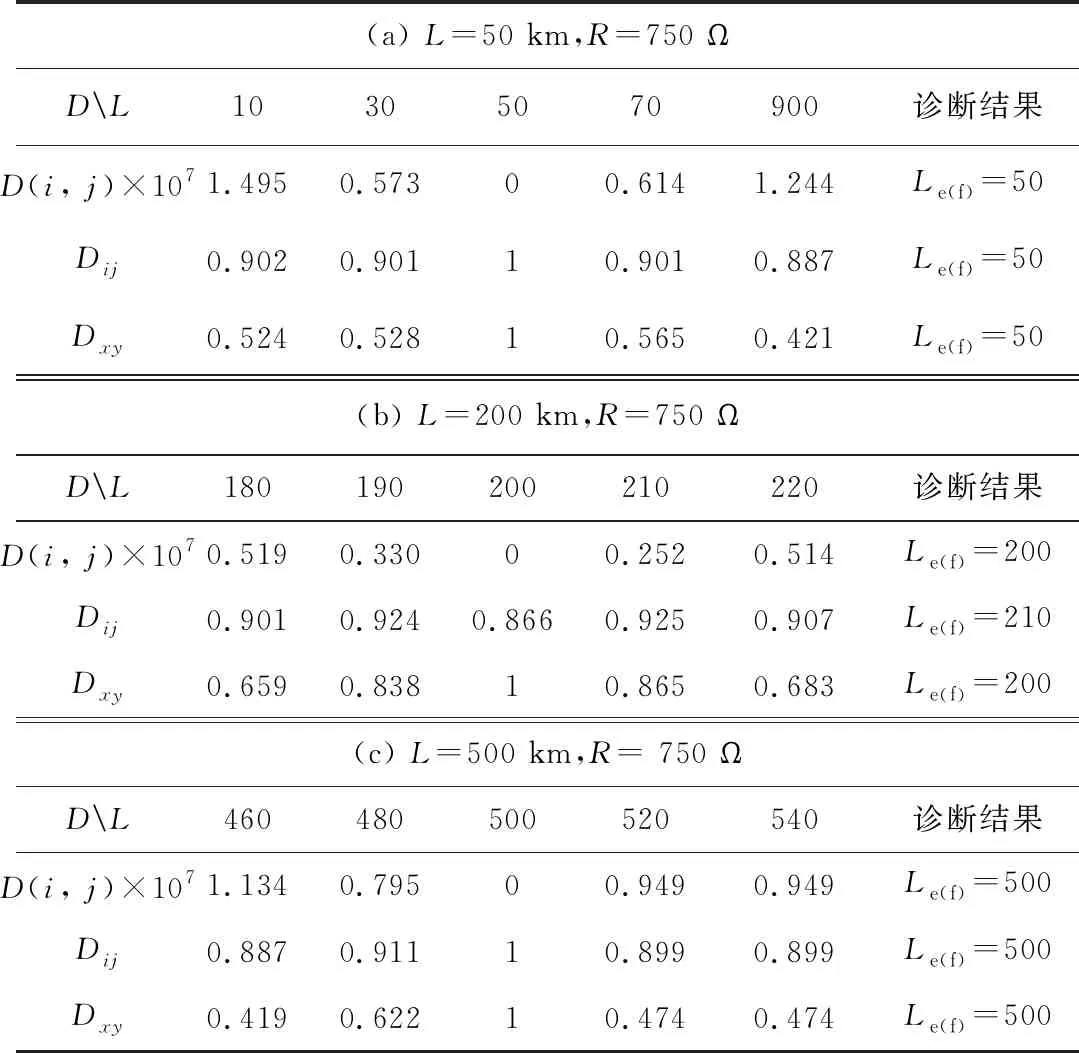
方法1:(动态时间规整与累积距离计算)根据 式(7)计算得到样本故障特征测序列Xi与实测Xj的累积距离D(i,j)。选定合适的阀值Dthr,当D(i,j) 方法2:(灰色关联分析与关联度计算)根据式(9)计算得到样本故障特征测序列Xi与实测Xj的关联度Dij。选定合适的阀值Dthr,当Dxy>Dthr时可判定实测特征信号与样本相似; 方法3:(时频谱矩阵相似度识别方法)根据式(16)计算得到样本故障时频谱特征序列Ei与实测Ej的相似度Dxy。选定合适的阀值Dthr,当Dij>Dthr时可判定实测特征信号与样本相似; (3)确定故障点位置和估计短路电阻大小 根据阀值Dthr选出相似度较高的样本,方法1和方法2分别确定最大Dij和Dxy值对应的样本与实测故障特征序列最相似,而方法3则是确定最小D(i,j)值对应的样本与实测故障特征序列最相似,由此三种方法可以进一步认为所选样本标注的故障点位置和短路电阻大小与模拟故障最为接近,如图4所示。 为了验证所述三种时频分析方法的可行性,并比较其故障诊断性能。建立如图1的三端柔性直流系统精确模型,模拟不同条件下的极间短路故障,着重分析3 μs~10 μs内的暂态响应时频特征。 图4 故障诊断流程图 依次模拟距离测点50 km、200 km和500 km处经750 Ω电阻的短路故障,采用所述三种方法计算不同故障点位置下实测故障特征曲线与所有样本的D值,得到D值大小与所有样本故障点距离L的相关性曲线以及诊断结果如图5和表1所示。 图5中方法1的分析结果表明:当Dthr<107时,D(i,j)值大小显著减小,且存在最小值D(i,j)值,对应样本的故障点位置与模拟位置基本吻合。 在图5中方法2分析结果中:(1)故障点距离L为50 km和500 km所对应的暂态响应特征曲线上,当Dthr>0.95时,Dij值大小较大,且存在最大值Dij值,其对应样本的故障点位置与模拟故障位置基本吻合;(2)故障点距离L为200 km对应的关联度Dij随故障点位置变化曲线上有非连续畸变,可能导致误诊断故障点为210 km处,如表1(b)所示。 图5中方法3的分析结果表明:当Dthr>0.8时,Dxy值大小较大,且存在最大值Dxy值,其对应样本的故障点位置与模拟故障位置基本吻合。 图5 D值随样本故障点距离L变化曲线 表1 不同故障点位置下的诊断结果 设故障点为离测点250 km处,依次模拟经50 Ω、800 Ω和1 600 Ω电阻发生短路故障,采用所述三种分析方法计算不同大小短路电阻时实测故障特征曲线与所有样本的D值,得到D值大小随电阻变化的曲线以及诊断结果如图6和表2所示。 图6 D值随短路电阻Rd变化曲线 表2 不同短路电阻时的诊断结果 图6中R=50 Ω对应的特征曲线上,当R较小时,D值大小随短路电阻R变化较快。在R=800 Ω和R=1 600 Ω对应的特征曲线上,当R较小时,D值大小随短路电阻R变化缓慢,此时通过D值大小来区分不同接地故障的准确性会下降。 图6中方法1对应的曲线中,R=50 Ω对应的故障特征曲线上,Dthr=0对应R值与模拟故障基本吻合,可以阀值Dthr=0作为判据。当电阻较大时,如图中R=800 Ω和R=1 600 Ω的故障特征曲线,以Dthr=0为判据,只能确定短路电阻大小的范围。 方法2、方法3的特征曲线变化特点与方法1类似,不同的是其判据阀值Dthr应取为1。另外,在方法2故障特征曲线中,关联度D随样本故障点位置变化曲线上有非连续畸变,会降低故障诊断准确性。 表2中,理论上方法1的阀值Dthr应接近0,但是实际中难以准确定量。方法1实际操作时要求欧氏距离时间序列严格对齐,需要进行预处理,与另外两种方法相比效率较低。 上述仿真分析表明: (1)通过精确建模和故障模拟来构建样本的思路可行,所述三种时频分析方法及其诊断判据有效; (2)与时域分析方法1、方法2相比,时频分析方法3得到的频域故障特征更为丰富,显著提高诊断性能。 对所述基于阻抗网络暂态响应时频特性的故障诊断方法进行以下理论建模和仿真分析验证: (1)建立柔性直流系统精确模型进而推导出故障网络阻抗表达式,通过理论计算或建模仿真可以得到注入脉冲的暂态响应特性曲线; (2)模拟不同故障点经不同大小电阻的短路故障,对暂态响应特性曲线进行时频变换和相似性分析得到D值随故障点位置和故障电阻大小的变化曲线,能够确定故障点位置和估计故障电阻大小; (3)通过仿真分析验证了所述诊断方法的可行性以及相应判据的有效性,且频域分析方法的诊断性能优于时域分析方法。4 仿真与分析

4.1 相同短路电阻、不同故障点位置的仿真分析

4.2 相同故障点位置、不同短路电阻的仿真分析


5 结束语

