IRS辅助毫米波MIMO系统波束赋形优化的低复杂度方案

王长江 傅友华

（1.南京邮电大学电子与光学工程学院、柔性电子（未来技术）学院，江苏南京 210023；2.南京邮电大学射频集成与微组装技术国家地方联合工程实验室，江苏南京 210023）

1 引言

第五代移动通信系统（5G）中大规模多输入多输出（Multiple Input Multiple Output，MIMO）技术通过分集增益所带来的巨大阵列增益，能够弥补毫米波技术所带来的传输损耗。毫米波与大规模MIMO技术的结合，使系统的容量得到显著的提升。虽然大规模MIMO 技术能有效解决毫米波的传输损耗问题，但是大量有源节点的部署导致了高硬件成本和高能耗，这给实际部署中带来了很大的挑战［1］。同时，基站、接入点或中继中多天线的部署无疑增加了信号处理的复杂度。超密集组网（Ultra Dense Network，UDN）设置下大量部署基站或接入点，不仅会增加硬件成本，还会加剧信号干扰问题［2］。智能反射表面（Intelligent Reflecting Surface，IRS）被认为是无线通信网络的前景技术之一，其通过智能重新配置无线传播环境，增强无线网络容量和覆盖的潜力，因此受到极大关注［3］。

IRS 由大量无源反射单元阵列组成，每个反射单元都可以独立地调整入射信号的幅值和相位。IRS 是无源器件，相对于传统的中继，IRS 的单元具有反射特性，不需要使用射频链，具有功耗低的优势。另外，IRS 是由电磁（Electromagnetic，EM）超材料制成的低成本器件，容易部署［3］。IRS 作为新兴的一种超材料，为了能够在实际生活场景中得到合理有效的应用，如何根据移动用户位置以及CSI 实时快速准确地调整入射信号的幅值和相位，也就是IRS 反射优化，使系统容量得到显著提升，是首要解决的问题。由于IRS是无源元件不具有接收和分析信号的能力，其反射优化设计也称为无源波束赋形（Passive Beamforming），常与有源设备联合设计有源和无源波束赋形。

目前有许多工作基于IRS 辅助的MISO 无线系统中的波束赋形研究［4］，而更加普遍适用的毫米波MIMO 系统主要通过并行传输多路数据流来提高其信道容量，故目标函数通常为对数-行列式形式，更加难以处理。文献［5］提出一种基于交替优化（Alternating Optimization，AO）的算法，在其他变量固定的情况下，每次迭代优化一个IRS 单元的相移或发射协方差矩阵，具体地，对于给定的发射协方差矩阵和任意N-1 个IRS 相移，剩余相移的最优解以闭合形式得到。基于AO 的方法不能将发射协方差矩阵和IRS 相移矩阵解耦，而且必须保证每次迭代的子问题是凸问题，另外AO 算法只能收敛到局部最优解，且复杂度较高。文献［6］提出采用块坐标下降（Block Coordinate Descent，BCD）算法进行交替优化预编码矩阵和相移矩阵，当固定相移矩阵时得到最优发射预编码矩阵的闭式解，而相移矩阵通过主最小化（Majorization-Minimization，MM）或复圆流形（Complex Circle Manifold，CCM）方法得到。虽然在解决子问题时提出了新的高效算法，总体算法本质上仍是交替优化的思想，但依然存在上述不足。文献［7］提出了一种基于遗传算法（GA）的搜索方案来获得IRS 相移矩阵，采用交替优化算法对有源波束形成和无源相移矩阵进行集成设计。然而GA 算法在IRS 恒模的高度非凸约束下很难保证其收敛性，且该算法具有较高的计算复杂度。文献［8］提出半正定松弛（Semi-Definite Relaxation，SDR）方法解决IRS 的反射系数的恒模约束，SDR 方法后跟足够多次随机化保证了最优值的近似值。SDR算法同样只能得到次优解，次优性能只能达到约78%，而且足够多次的随机化计算也增加了算法计算复杂度。在IRS 辅助的MIMO 系统研究中，现有工作没有将有源与无源波束赋形矩阵进行解耦，现有算法在只能得到局部最优解的情况下仍具有较高的计算复杂度，且在不能得到最优解的情况下也无法衡量现有次优算法的性能。

本文考虑一个单用户IRS 辅助的毫米波MIMO系统，其中多天线接入点（access point，AP）在IRS的辅助下服务多天线用户设备（user equipment，UE）。通过优化设计AP 端有源和IRS 无源波束赋形相移矩阵，以最大化频谱效率。具体地，首先将有源和无源反射相移矩阵解耦，得到在IRS 相移矩阵给定情况下的最优有源波束赋形解，将IRS 无源波束赋形设计问题推导为一个非凸二次约束二次规划（quadratical constraint quadratic programming，QCQP）问题；为了求解该非凸的QCQP 问题的无源波束赋形解，提出低复杂度的连续闭式解（successive closed form，SCF）算法求解方案，使用凸等式约束的二次规划（quadratical programming，QP）序列来解决非凸恒模约束；为衡量SCF 算法性能，对比了能得到最优解的分支界定（branch and bound，BnB）算法，经过凸松弛后不断划分其搜索空间直到收敛；仿真结果验证了SCF 算法在IRS 相移连续和离散时都具有低复杂度高频谱效率性能，而且对于离散相移IRS 的频谱效率接近最优性能，对在6G 中IRS 的部署和应用更具有实际价值和意义。

本文中，RM×N表示M×N的实空间，CM×N表示M×N的复空间。X*，XT，XH，X-1，X[：，1：n]表示矩阵X的共轭，转置，转置共轭，逆，1～n列。E[·]表示数学期望。对于复数a，|a|和arg(a)分别表示a的模和相角，Re(a)和Im(a)分别表示a的实部和虚部。diag(a)表示对角元素为向量a的对角矩阵，Diag(X)表示矩阵X的对角元素组成的向量。1表示全为1 的列向量。z～CΝ(0，σ2)表示z服从均值为0方差为σ2的复高斯分布。⊗表示Kronecker积。

2 系统和信道模型

如图1 所示，考虑一个单用户IRS 辅助的毫米波MIMO 系统。其中，接入点（AP）配备Nt根的ULA（uniform linear array）发射天线，用户设备（UE）配备Nr根接收天线。IRS由N个URA（uniform rectangular array）的无源反射元件组成。理想情况下，AP 可直接发送对准用户的波束，而当AP-UE 视距链路不理想或者被阻挡的情况下，IRS 可提供AP-UE 之间的波束传输的视距链路，起到辅助作用。IRS 所有元件的反射系数由AP 根据实时CSI（channel state information）通过FPGA Controller 控制，以更好地辅助信号传输。本文中，假设AP 对于所有信道的CSI是完全已知的，另外，由于被IRS反射多次的信号功率存在较大损耗，因此可以忽略不计。

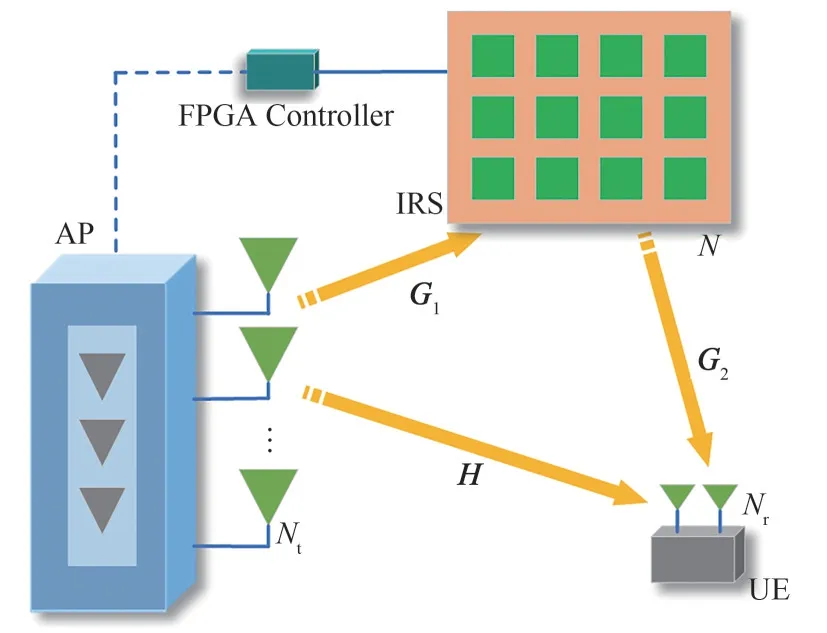
图1 IRS辅助的毫米波MIMO无线系统Fig.1 IRS-assisted millimeter wave MIMO wireless system

根据毫米波信道常用的Saleh-Valenzuela 信道模型［9］，因此可将AP与IRS之间的信道G1表示为

其中，0≤x＜Nx，0≤y＜Ny，0≤z＜Nt，Nx和Ny分别为IRS 元件阵列在x 轴和y 轴的个数，IRS 反射元件个数N=Nx×Ny；λ为毫米波信号的波长，d为相邻天线或IRS 反射元件的间隔距离，一般认为天线间距为波长的一半，即d=。

IRS 与UE 之间的信道G2和AP 与UE 之间的信道H与上述G1类似，分别可表示为

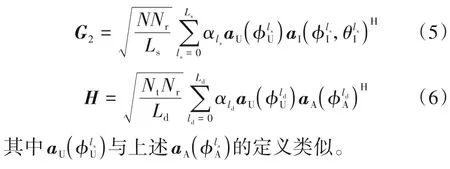
3 问题表述

通过优化AP 端有源波束赋形F和IRS 反射波束赋形矩阵Θ，以最大化毫米波MIMO 系统的频谱效率。最大化系统频谱效率的优化问题可表述为

该优化问题是一个非凸问题，因为目标函数对于IRS 反射波束赋形矩阵Θ是非凸的，并且θn的恒模约束同样是非凸的。而且F和Θ的耦合也使得问题难以求解。经过对矩阵(G2ΘG1+H)F奇异分解以及应用Jensen 不等式的性质［10］，可将问题P1近似转化为

在优化问题P2中，为了解决F和Θ的耦合问题，F采用最优基带波束赋形。因此，假设IRS 相移矩阵Θ给定的情况下，最优波束赋形矩阵为［11］

其中，Vtot由总信道Htot=G2ΘG1+H奇异值分解之后的右奇异向量组成。也就是说，最优有源波束赋形矩阵由Ns个最大奇异值对应的酉向量组成。在此基础上，假设Ns=Nr≤Nt，因为Fopt为酉矩阵，由矩阵论的知识可知，因此可将F和Θ解耦，优化变量只有Θ的问题重新表述为

考虑P3中的目标函数

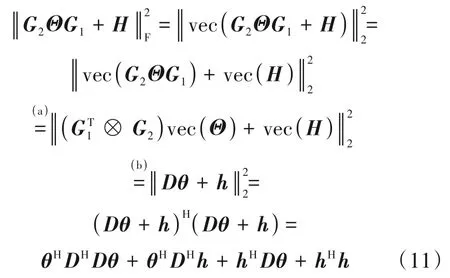
其中(a)成立是因为存在基本等式vec(ABC)=(CT⊗A)vec(B)［12］；由于Θ是一个对角阵，vec(Θ)中只含有N个非零元素，所以定义θ=Diag(Θ)=[θ1，θ2，…，θN]T；定义j∈Snz为vec(Θ)中所有非零元素的位置索引，令D=，h=vec(H)，因此(b)成立。式(11)中最后一项hHh与优化变量θ无关，因此可省略。因此优化问题P3可写为

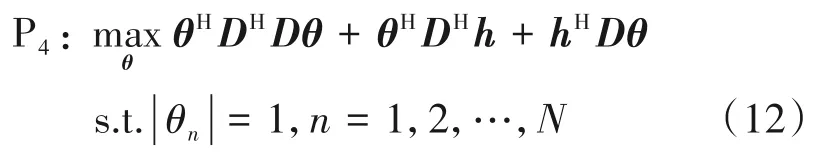
以上将优化问题P1转化为P4，P4解决则整个问题解决。P4是一个非凸二次约束二次规划（QCQP）问题，只有唯一的恒模约束造成优化问题非凸。下面将提出低复杂度的连续闭式解（SCF）算法求解方案，并且对比分析基于BnB 的全局最优搜索算法以验证SCF算法性能。

4 低复杂度的连续闭式解求解方案

为了解决P4中高度非凸的恒模约束，提出低复杂度的连续闭式解（SCF）求解无源波束赋形方案。该算法使用凸等式约束的二次规划（QP）序列来解决非凸恒模约束，每个二次规划都有一个封闭形式的解，并且在收敛时得到恒模解。首先将P4中目标函数进行转化，令P=-DHD，q=DHh，P4可写为

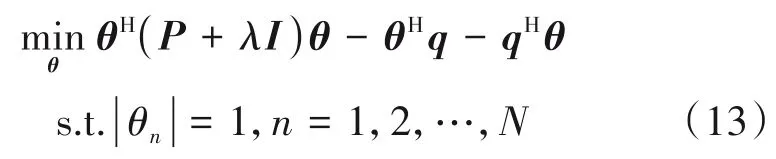
由于θ的恒模约束，所以λθHθ=λN是一个常数，因此上述变化不影响最优解。然后将问题进一步转化为下面的实值问题

其中

问题(14)实际约束了θ中每个元素的实部与虚部的平方和等于1，与模1 约束等价。其中En是一个2N×2N的矩阵，定义为

下面构造等式约束的QP序列

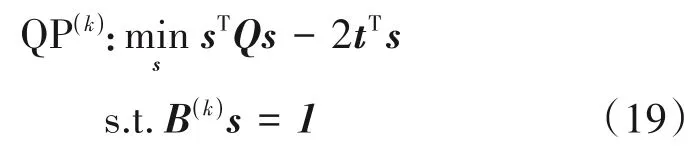
其中μ(k)为拉格朗日乘子。因此求解上述KKT 条件可得问题(19)的最优解为

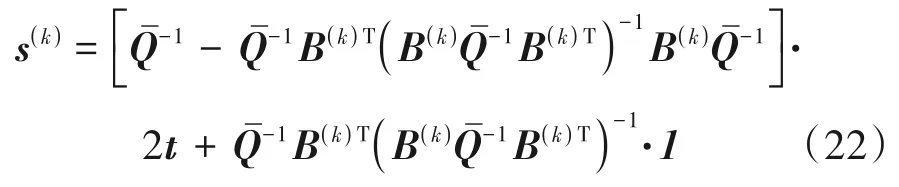
虽然优化问题(19)的最优解并非恒模，但随着序列QP(k)的求解保证了目标函数值的非递增性，并且可以收敛到恒模解。问题QP(k)的可行域由问题QP(k-1)的最优解θ(k-1)决定，具体地，的迭代规则保证了QP(k)的可行域为经过θ(k-1)的圆的切线。假设s(k-1)为QP(k-1)的最优解，有B(k)s(k-1)=1，利用三角代换关系可证明B(k)s(k-1)=1，即问题序列QP(k)的可行域包含θ(k-1)，另外QP(k)的目标函数值随k不递增，即f(θ(k-1))≥f(θ(k))，具体证明见文献［13］。序列QP(k)的迭代求解和收敛过程如图2（a）所示，在算法1中总结了SCF算法的完整步骤。

为了衡量所提低复杂度的SCF 算法的性能，下面应用分支界定（BnB）算法求解无源波束赋形矩阵的全局最优解来对比分析。BnB算法是一种系统的搜索算法，通过规律地枚举求解多个子问题，进而找到最优解［14］。因此BnB 算法的前提是子问题可解，所以P4中的恒模约束必须进行凸松弛。为了表述清楚下面用vn表示单位圆上的点，而cn表示圆内的点，其中n=1，2，…，N。如图2（b），假设arg(vn)∈[ln，un]，那么vn的范围可表示为紫色圆弧An。P4可重新表示为

图2 （a）SCF算法QP序列的求解和收敛，（b）BnB算法凸集和分支表示Fig.2 （a）Solving and convergence of SCF algorithm QP sequence，（b）BnB algorithm convex set and branch representation

先将(23)中|vn|=1 的约束松弛为|cn|≤1，在图2（b）中为圆弧An和两个半径围成的区域，显然已经是一个凸集。然后去掉中的三角区域，只考虑vn∈An的最紧的凸集是由紫色圆弧An与An的两个端点连成的弦之间的区域。优化问题P4经过凸松弛之后的优化问题为

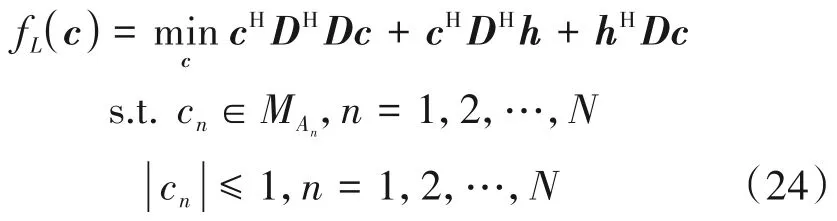
优化问题(23)中cn∈的约束等价于

其中arg(cn)∈[ln，un]，an=，具体证明过程见引理。上述经凸松弛后转化为凸问题，可通过内点法求解。问题(24)得到的解显然也不能保证恒模解，下面通过BnB算法的搜索策略将搜索空间不断缩小以逼近单元圆，使之收敛到全局最优解。

优化问题(23)的搜索空间可以看成N个单位圆的乘积，即A=A1×A2×…×AN=[0，2π]N。为了使BnB 算法能够尽可能快速收敛，需要仔细设计算法中确定上下界、节点选择规则和分支规则三个重要因素，分别具体说明［14］：

（1）确定上下界。对于要求解的每个子问题，求解其对应的凸问题，得到最优解c，最优值作为该子问题的下界，即Lb=fL(c)。可行域中任意一个点都可以确定上界，因此令v=，如同图2（b）中的点cn投影到圆弧上的点vn，即上界Ub=fU(v)。

（2）节点选择规则。每次迭代应当选择一个叶子节点，然后进行分支操作和求解其上下界。节点选择通常与优化目标有关，对于(23)最小化问题，选择所有叶子节点中下界最小的节点。

（3）分支规则。对上一步选择出来的子问题（节点），假设其最优解为c，v=，找到c与v距离最远的元素索引n，即n=。然后将An进行均匀划分，设An=[ln，un]，令z=，将搜索空间A在An的区间中间点z处均匀划分为Al和Ar，其中

根据SCF 算法迭代求解QP(k)的次数，其计算复杂度为O(KN2.373)，K为总迭代次数［15］。BnB 算法搜索树的大小随N呈指数增长，对于给定的收敛容限ε，其达到ε最优解的所需要的迭代次数最多为，其中δ=。基于BnB的搜索算法固然可以得到全局最优解，然而代价却是极高的指数复杂度。还有，交替优化（AO）算法的计算复杂度为O(NrNt(N+Nr)r+)，其中，Nr≤Nt，K为迭代次数，r为随机数［6］。采用随机化的半定松弛（SDR）算法的计算复杂度为O(N3.5)+O(TN2)，其中T≫N为随机化的次数［17］。因此，相对于BnB、AO 和SDR算法，SCF算法具有更低的计算复杂度。

5 仿真结果分析

下面给出在所考虑无线通信系统中的仿真结果。AP 端配备Nt=32 根发射天线，UE 端配备Nr=4 根接收天线，发送数据流数Ns=4。AP 的位置设置在坐标轴的原点(0，0)处，UE 的位置在一个圆心在(40，0)半径为10 m 的圆形区域内随机产生，IRS的位置固定在坐标(40，10)处。总发射功率P=30 dBm（若不另外说明），噪声功率σ2=-85 dBm。复信道增益～CN(0，10-0.1κ(d))，其中κ(d)=ρa+10ρblg(d)+γ，其中γ～，ρa=61.4 dB，ρb=2 dB，ρc=5.8 dB，d为收发设备之间的距离［18］。和的定义与类似。

图3 研究了SCF 算法在IRS 的反射元件数N=15和N=25时的收敛性，收敛容差设置为ε=10-5。可以看到在迭代开始时目标值快速下降，后面则下降缓慢，直到相邻两次的目标值不超过ε停止迭代。图4 研究了BnB 算法同样在N=15和N=25 时的收敛性，收敛容差同样设置为ε=10-5。图中可以看到随着迭代次数的增加，上界和下界的距离越来越近，直到小于ε迭代结束。因为搜索树的大小随N呈指数型增加，也就意味着为了得到全局最优解，随着N的增加其复杂度也大大增加。由于每次迭代的次数不一，为了说明问题，图3 和图4 是经过多次测试取平均的结果。SCF算法的迭代次数不仅小于在相同设置下的BnB 算法，而且每一次迭代所需时间也远小于BnB算法。

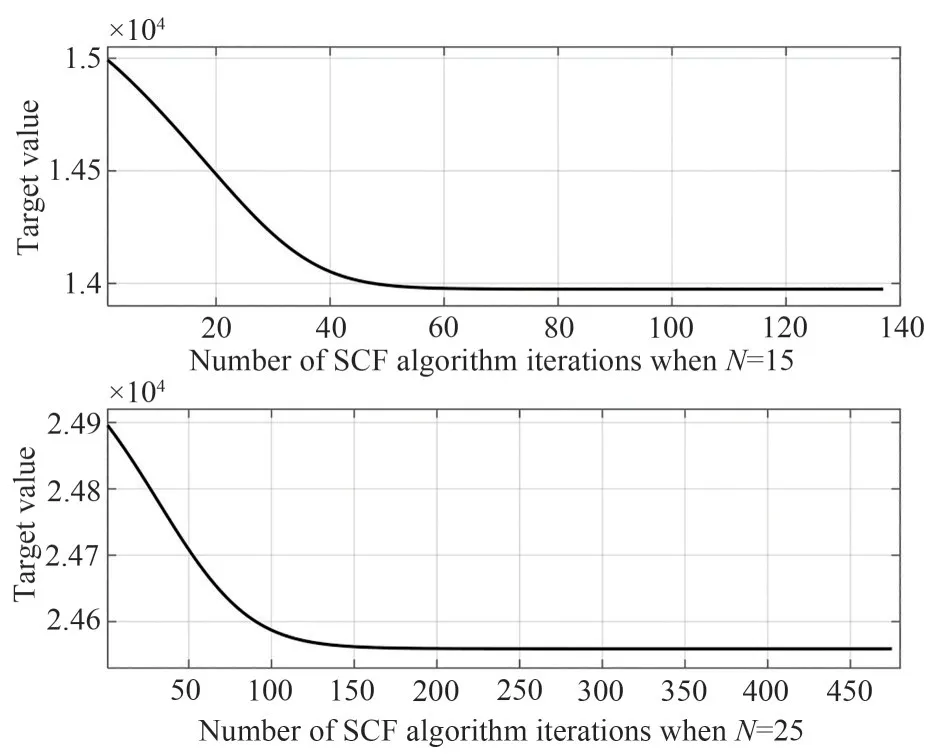
图3 SCF算法的迭代和收敛过程Fig.3 Iteration and convergence process of SCF algorithm

图4 BnB算法的迭代和收敛过程Fig.4 Iteration and convergence process of BnB algorithm

图5 研究了系统频谱效率与IRS 反射元件数N的关系。图中可以看到BnB 算法在不同的N都具有最高的频谱效率，SCF 算法则低于BnB 算法的性能，但明显高于SDR 算法所具有的频谱效率，最低的曲线则是当IRS相移矩阵随机设置，而AP端采用最优有源波束赋形矩阵Fopt时的性能曲线，可作为基准性能。还可以看到，随着N的增大不同算法之间的性能差距越大，这也间接说明了研究高质量低复杂度次优算法和最优算法的价值所在。

图5 系统频谱效率与IRS反射元件数N的关系Fig.5 The relationship between the system spectrum efficiency and the number N of IRS reflection elements

图6 研究了SCF 和BnB 算法分别在连续相移、1 bit、2 bit 量化相移时N与系统频谱效率的关系。考虑bbit 量化时，离散相移角度集合Dset={2π·(0：2b-1)/2b}，那么离散相移角

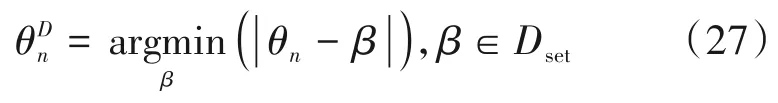
图6 不同反射元件数N时IRS连续和离散相移的频谱效率Fig.6 Spectral efficiency of IRS continuous and discrete phase shifts with different numbers of reflective elements N

即在离散相移角度集合中选择一个与最优连续相移解距离最近的离散角。图6 中可以看到，连续相移时二者性能则同图5 所表示的一致，而当1 bit 和2 bit 量化相移时，低复杂度的SCF 算法所具有的频谱效率已经十分接近最优的BnB 算法的性能曲线。这说明在很多情况下SCF 算法的离散量化相移与最优的BnB 算法所得到的是一致的，尽管在相移连续时二者存在差距。与图5结果相似，图6中随着N的增大，SCF 算法的频谱效率与BnB 的差距有所增加，但可看到当N=30 时二者在连续相移时只有，而在离散相移时差距更小。BnB 算法在较大的N时虽然能够取得全局最优解，但同时其代价是承担了随N增加的指数级的计算复杂度；SCF算法则在与最优性能差距不大的情况下大大降低了计算复杂度。

图7 研究了系统频谱效率与总发射功率P的关系。其中，IRS 反射元件数N=20，其余参数与上述相同。与图5 中具有相似的结果，BnB 算法在不同的发射功率P都具有最高的频谱效率，SCF 算法略低于BnB 算法的性能且十分接近，且明显高于SDR算法在不同发射功率P所具有的频谱效率，最下面的曲线依然是IRS相移矩阵随机和最优有源波束赋形矩阵Fopt组合时的基准曲线。

图7 系统频谱效率与总发射功率P的关系Fig.7 The relationship between system spectrum efficiency and total transmit power P

图8 研究了SCF 和BnB 算法分别在连续相移、1 bit、2 bit 量化相移时总发射功率P与系统频谱效率的关系。在连续相移时则同图7 所表示的一致，而在当1 bit 和2 bit 量化相移时，在不同的发射功率下，SCF 算法所具有的频谱效率略低于BnB 算法的性能曲线，可以得到与图6相同的结论，虽然SCF 算法在连续时与最优BnB 算法存在一定差距，但在相移离散时二者的性能差距非常之小，由此可见，低复杂度的SCF在相移离散时具有十分优异的性能。

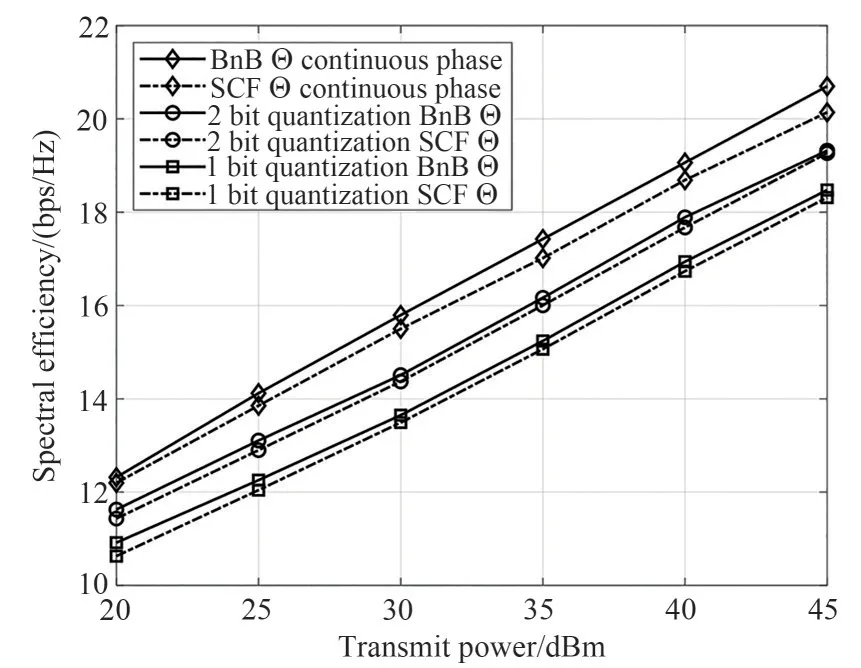
图8 不同总发射功率P时IRS连续和离散相移的频谱效率Fig.8 Spectral efficiency of IRS continuous and discrete phase shifts at different total transmit power

尽管在理论研究中通常认为IRS 相移连续，但是在实际应用中IRS每个反射单元均是由开关元件（比如PIN二极管、场效应晶体管）组成，因此具有的相移比特数越多，则需要的开关元件越多从而成本越高。因此从上述仿真验证结果可知，本文提出的SCF 算法不仅具有较低的复杂度，而且对于离散相移的IRS 无源波束赋形的频谱效率接近最优性能，对在6G 中IRS 的部署和应用更具有实际价值和意义。

6 结论

本文考虑一个单用户IRS 辅助的毫米波MIMO系统。通过优化设计AP 端有源和IRS 无源波束赋形相移矩阵，以最大化频谱效率。具体地，首先将有源和无源波束赋形矩阵解耦，得到在IRS 相移矩阵给定情况下的最优有源波束赋形解，将IRS 无源波束赋形设计问题推导为一个非凸QCQP 问题；提出了低复杂度的SCF 算法求解方案，使用凸等式约束的二次规划（QP）序列来解决非凸恒模约束；为衡量SCF 算法性能，对比能得到最优解的分支界定（BnB）算法来解决恒模约束，经过凸松弛后不断划分其搜索空间直到收敛；仿真结果验证了SCF 算法在IRS相移连续和离散时都具有低复杂度高频谱效率性能，而且对于离散相移IRS 的频谱效率接近最优性能，对在6G 中IRS的部署和应用更具有实际价值和意义。SCF算法对解决带有恒模约束的高度非凸问题提供了重要解决思路和方案，后续将考虑应用于多用户场景中深入展开分析和研究。

附录

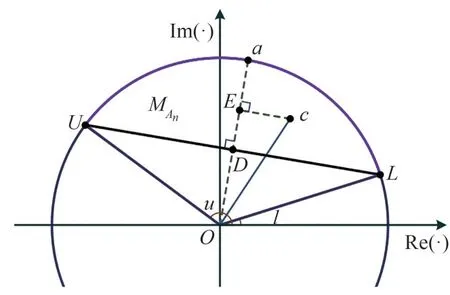
图9 凸集中任一点c所满足的等价条件Fig.9 The equivalent condition satisfied by any point c in the convex set

当u-l∈[0,2π]时，上述结论在数学上依然成立。