机床结构对流换热系数的参数化建模方法＊

毛晓博 史建猛 雷 声 毛宽民

（①中航西安飞机工业集团股份有限公司，陕西西安 710089；②中南民族大学计算机科学学院，湖北武汉 430074；③华中科技大学机械科学与工程学院，湖北武汉 430074）

调查表明数控机床在精密加工过程中热误差能够占到总误差的40%～70%[1]，高端数控机床的精密加工热误差甚至达到了70%以上[2]。热分析是研究控制数控机床热误差的重要方法之一，但热分析中的关键参数对流换热系数(convective heat transfer coefficient,CHTC)却因受到流体物理性质、换热部件表面位置、形貌、流体与换热部件表面温差和流速等因素的影响，计算极其困难，且CHTC的准确性对数控机床结构热分析的结果影响很大。

曹祎等[3]将飞机外部CHTC视为恒定数值的参考温度法进行改进，考虑到飞机结构影响，提出了一种求解飞机机体各区域外部CHTC仿真计算方法，并与传热公式法对比，验证了仿真方法的有效性。Li Y等[4]基于逆热传导理论，对CHTC计算进行优化，在ANSYS中对主轴温度场进行了模拟与热误差分析，通过仿真结果与实验数据的对比，验证了热对流系数优化的正确性和有效性。片锦香等[5]采用蜂群算法对机床主轴零件表面与空气的换热系数进行优化计算，通过迭代寻找最优解，得到的主轴CHTC精度更加准确。阳红等[6]构建RBF神经网络算法计算主轴的CHTC，将实验数据引入RBF网络中，增加了算法的可靠性与准确性。

上述方法在计算中均忽略了环境温度对CHTC的影响，甚至大多数在热分析中采用恒定的CHTC数值。机床在达到热稳定前，机床运行产生的热量会使机床结构的温度逐渐升高，机床结构换热表面的温度与环境的温差会随之增大，而CHTC是一个与温差相关的物理量，因此随着机床结构温度的升高，其与外界环境的CHTC会因其与环境温度的温差变化而变化[7]。因此在热分析中采用固定不变的CHTC必然增加分析误差。基于传热学理论，结合实验数据采用多元线性回归分析，提出一种考虑环境温度与温差变化的CHTC参数化计算方法，提升了CHTC计算精度及机床结构热分析的准确性与便捷性，为减小机床热误差研究提供一种高效准确的方法。

1 对流换热系数的参数化模型

结合牛顿冷却定律与流体流过机床结构表面的传热理论，将影响对流换热过程的物理量进行归纳分析，建立CHTC影响变量的参数化模型，如式（1）所示。

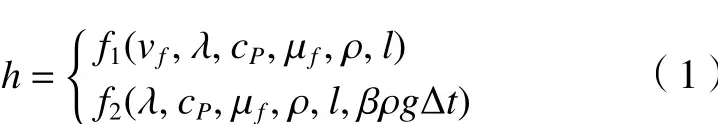
式中：f为CHTC与影响变量之间的函数映射关系；f1表示非自然对流状况下的函数关系式；f2表示自然对流时温差引起的升浮力下的函数关系式；其他参数表示的意义及单位如所示。

式（1）中8个物理量，包含长度量纲L、质量量纲M、时间量纲T和温度量纲θ共4个基本量纲。将这8个物理量的单位转化成4个基本量纲表示的形式，如表1所示。关系式，有n=7，r=4。即有

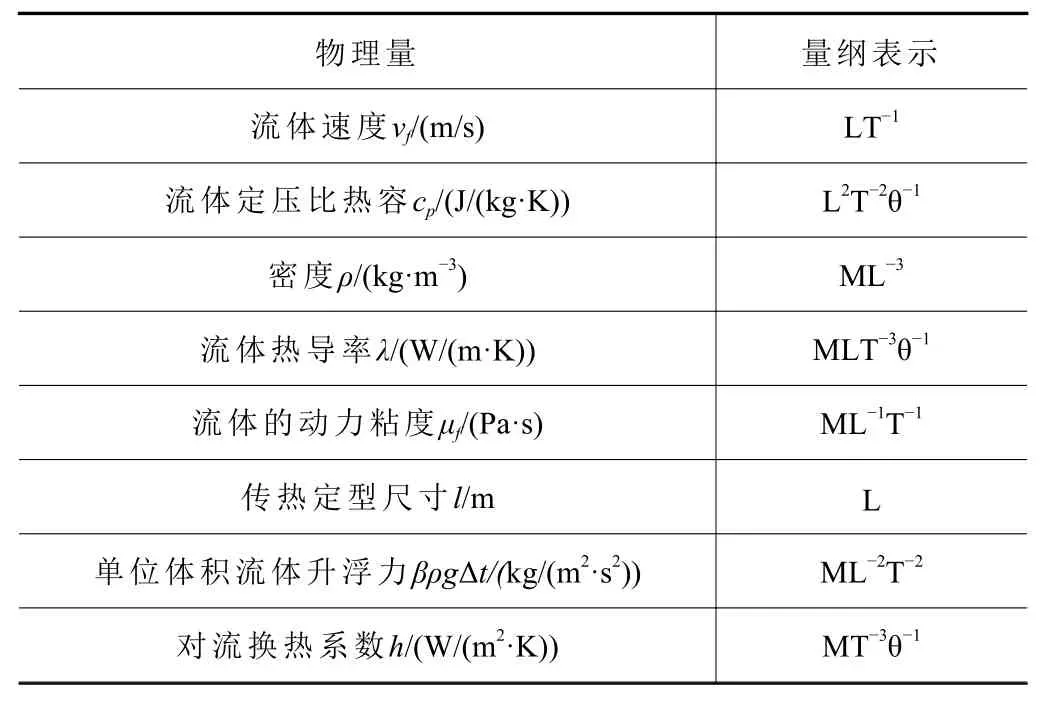
表1 CHTC参数化模型中基本量纲表示

根据π定理，物理方程量纲一致时，可用一组量纲为1数群的零函数表示。式（1）中f1的函数

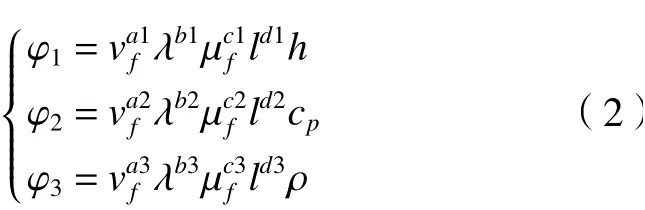
式中：φ1、φ2和φ3为3个无量纲参数；a、b、c、d为引入的指数参数。

将φ1按照量纲展开，参数a1=0、b1=-1、c1=0和d1=1，代入式（2）得到

同理得到

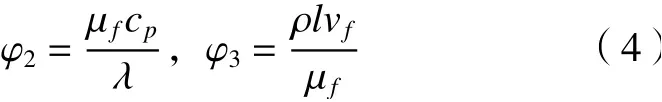
式（1）中f2表示的关系式，同理有

2 考虑温差变化的对流换热系数计算

2.1 对流换热系数的计算原理

结合机床结构传热过程的有限元分析和实验数据，提出如图1考虑环境温度与温差变化的CHTC计算方法。

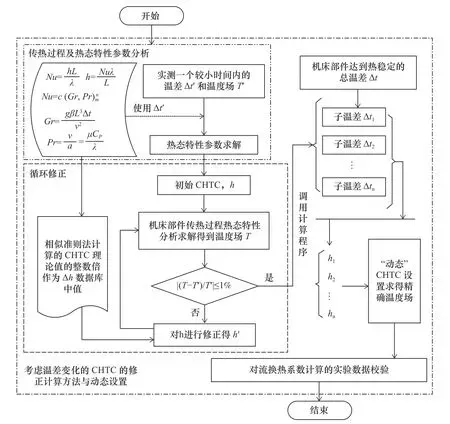
图1 环境温度与温差变化的CHTC计算原理

（1）传热过程及热态特性参数分析。测量一个较小时间段内温差Δt′和相应的温度数据，根据相似准则求得初始CHTC。

（2）CHTC的迭代修正计算。采用初始CHTC进行热分析，将热分析结果与实验测量值判断，进行迭代修正。算法修正采用文献[6]和文献[8]等中给出的，在机床有限元温度场仿真计算中，CHTC的参数取值一般是理论计算值的3～10倍。故将CHTC理论计算值的整数倍作为△h数据库中的数值。迭代修正时，为防止迭代中出现加减整数倍△h仍不能满足判断条件时，在循环计算中添加对当前整数倍△h做出减半甚至做1/4处理的命令，直到满足判断条件为止。

（3）考虑环境温度与温差变化的CHTC修正计算。根据环境温度预估机床的总温差，以1℃为等差间隔分成多个温度逐渐升高的子温差区间，采用修正计算方法求得各子温差区间对应的CHTCs，在热分析中给出动态加载方法，从而消除温差变化对CHTC计算的影响，进一步提高温度场模型的精确度。

2.2 对流换热系数计算流程分析

（1）引入实验数据，选取初始一小时间段内调用经验公式计算初始CHTC。

（2）采用步骤1计算的CHTC得到的仿真温度场与实验测量值对比，根据判断条件进行循环修正，提高CHTC的精度。

（3）对预估总温差进行多温度子区间的划分，在多温度区间下对多个CHTC的循环修正计算。

3 基于实验数据的对流换热系数的参数辨识方法

3.1 机床部件的热测试实验

热测试实验对象为沈阳机床集团生产的TC500立式钻攻中心的X轴滚珠丝杠进给系统（含工作台）。热实验工况设计如下：滚珠丝杠进给系统工作台在X轴方向上做往复运动。运动行程L=400 mm，滚珠丝杠进给系统的进给速度vg=4 m/min。电机的转速n=267 r/min，工作台运行时间为机床达到热稳定状况的4 h。

热实验中温度测点的选择及有限元模型如图2和图3所示。

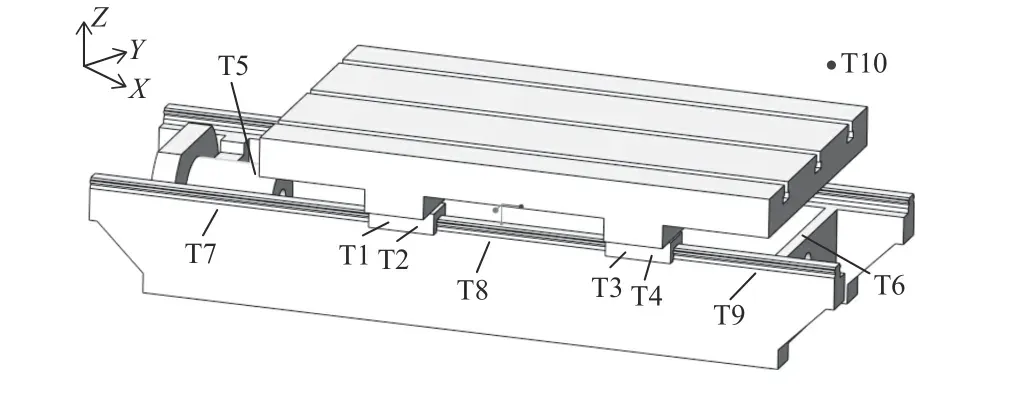
图2 几何模型及温度测点

图3 实验对象的有限元模型

采用PT-100三线制热电阻温度传感器、Agilent 34970A温度采集仪等搭建的实验测试平台如图4所示。

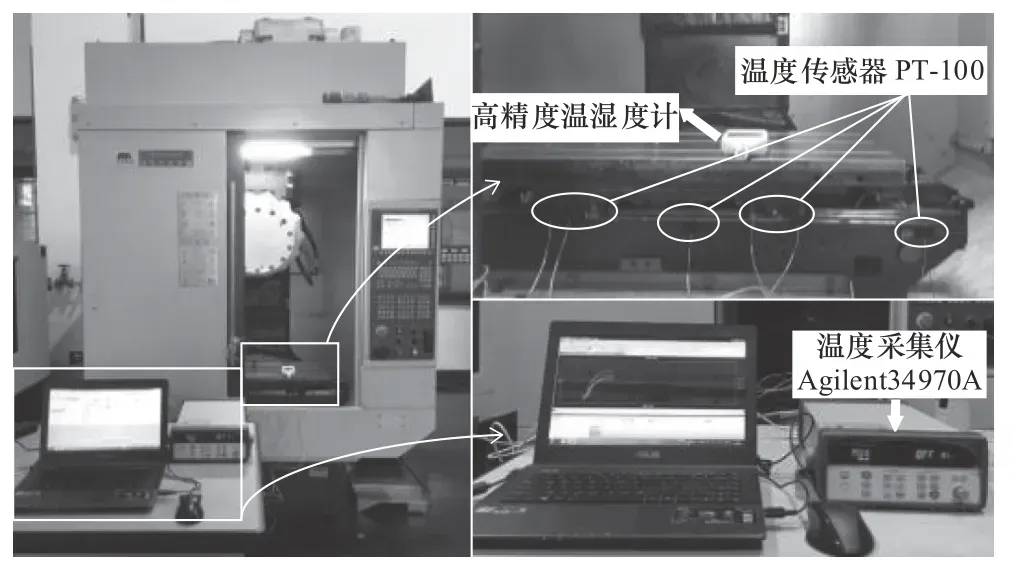
图4 热态热性实验测试平台

3.2 热载荷及结合面热阻

滚珠丝杠螺母产生的热量按照丝杠螺母与丝杠两端轴承的距离，根据热传导理论，分别传递到滚珠丝杠两端的轴承上进行间接加载。热分析中结合部间接触热阻及结合面传热，如表2所示。根据机床结构传热过程中的生热模型，得到滚珠丝杠进给系统各生热位置的热流密度如表3所示。

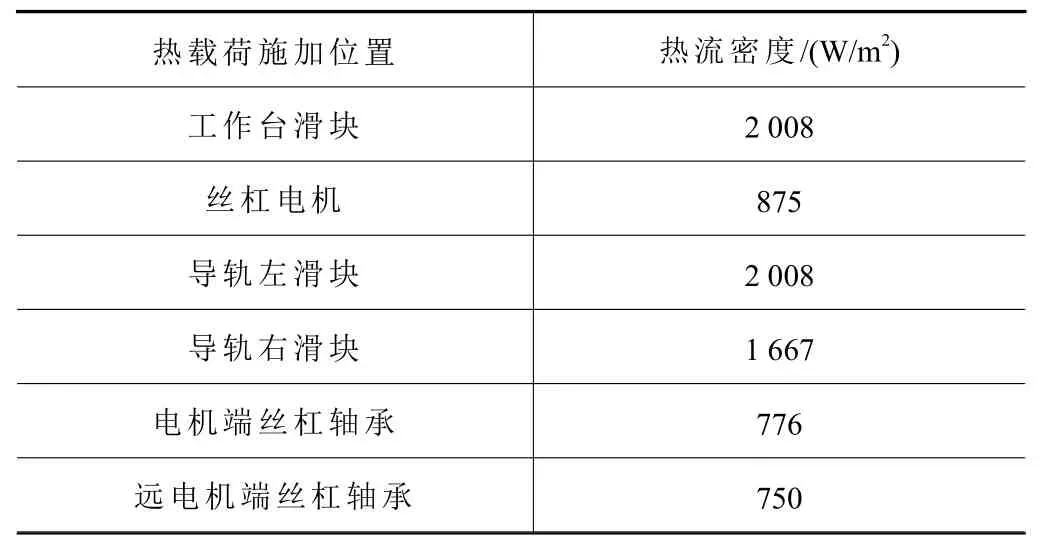
表2 生热部位的热流密度

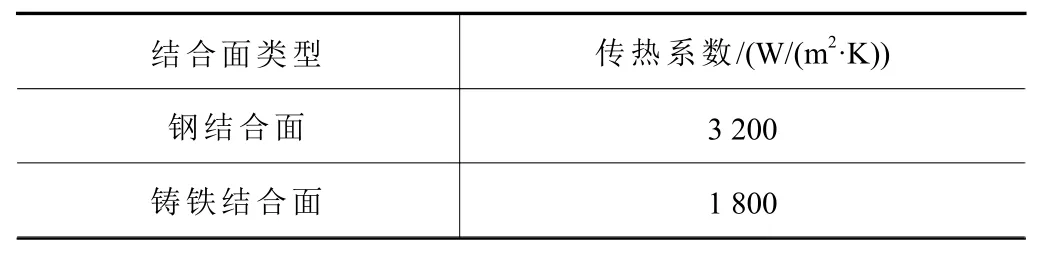
表3 结合面传热系数[9]

3.3 热分析中边界条件的动态加载

CHTC与环境温度和温差有很大的关联。温差发生变化，CHTC也会随之发生变化，即对流换热系数h会随着Δt的变化而变化。采用有限元软件ABAQUS将迭代修正计算的多个CHTCs分别施加到对应子温度区间，形成动态边界条件的参数加载，如图5所示。

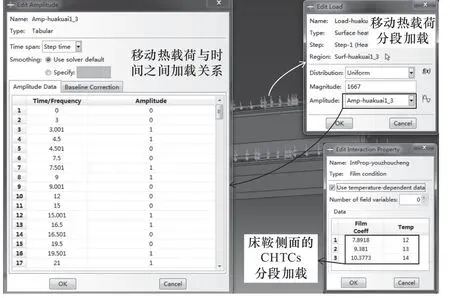
图5 动态边界条件加载的实现

4 对流换热系数的参数化计算方法

基于相似准则，采用有限元迭代计算可求得机床结构的对流换热系数，但这种方法对于复杂结构的多个CHTC计算效率极低。结合实验数据，对上述方法进一步改进，提出对流换热系数的参数化计算方法。

4.1 对流换热系数的参数化方程

在数控机床中，最常见的换热表面形状为矩形板，故以数控机床中使用最多的平板类换热表面为例，根据线性回归模型，建立其自然CHTC与环境温度t、温差Δt及换热表面特征尺寸l之间的线性回归方程为

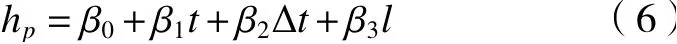
结合滚珠丝杠进给系统热实验数据，利用线性回归求得式（6）中的系数。得到对流换热系数hp与t、Δt、和l的参数化方程为

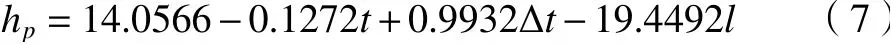
计算中拟合优度为0.956 8，统计量为22.152 8，显著性为0.015 0，剩余方差为0.500 9，说明方程具有可靠性。

在机床中，除过大多数水平板状换热特征尺寸外，圆柱形的换热部件也不少，同理结合横圆柱的自然对流换热与实验数据，利用回归分析，可得到横圆柱形状的对面换热系数hc与t、Δt、和l的方程为

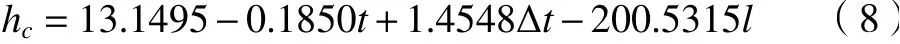
计 算中 拟 合 优 度为0.991 7，统 计 量F为119.253 4，显著性p=0.001 3，剩余方差为0.096 4，说明拟合结果准确。

式（7）、（8）分别以机床床鞍侧面和丝杠联轴器为例，且大量的实验数据是在机床部件与空气的自然对流换热过程中测量。

将数控机床中换热部件的类型及特征尺寸l的计算方法归纳如表4所示。后续计算机床热分析中平板类与圆柱类部件的自然对流换热系数时，确认了t、Δt、和l后，即可采用式（7）和式（8）进行快速地计算，可以看出参数化计算方法对CHTC的计算效率有着极大的提升。

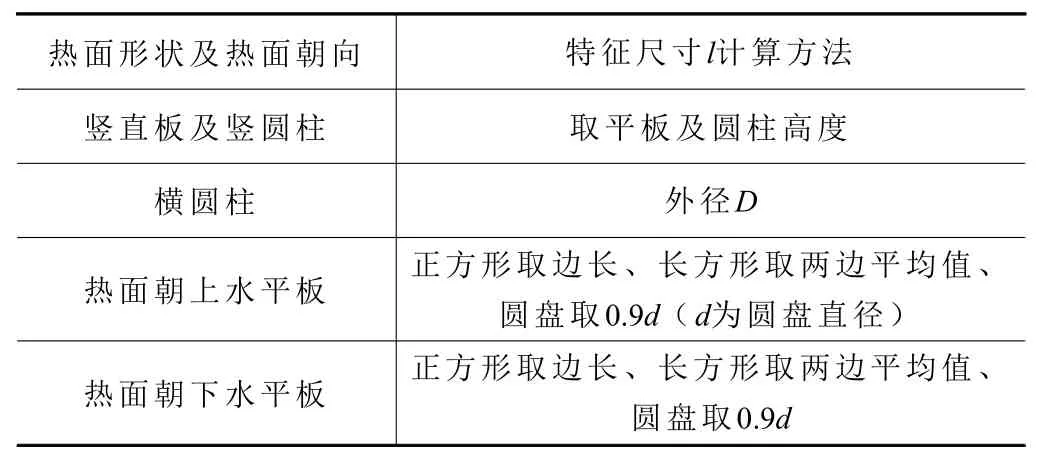
表4 机床换热部件特征尺寸计算方法[7]

4.2 参数化建模计算方法的验证

4.2.1 温度场对比分析

采用3.1节的滚珠丝杠进给系统对文中提出的参数化方法进行实验验证。采用传统相似准则法计算的CHTC进行热分析，得到滚珠丝杠进给系统床鞍与工作台的温度场如图6所示；采用参数化方法计算的到CHTC进行热分析，得到的温度场如图7所示。

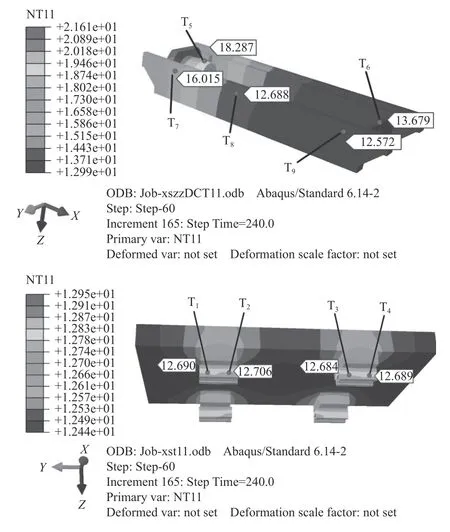
图6 相似准则法计算CHTC热分析结果

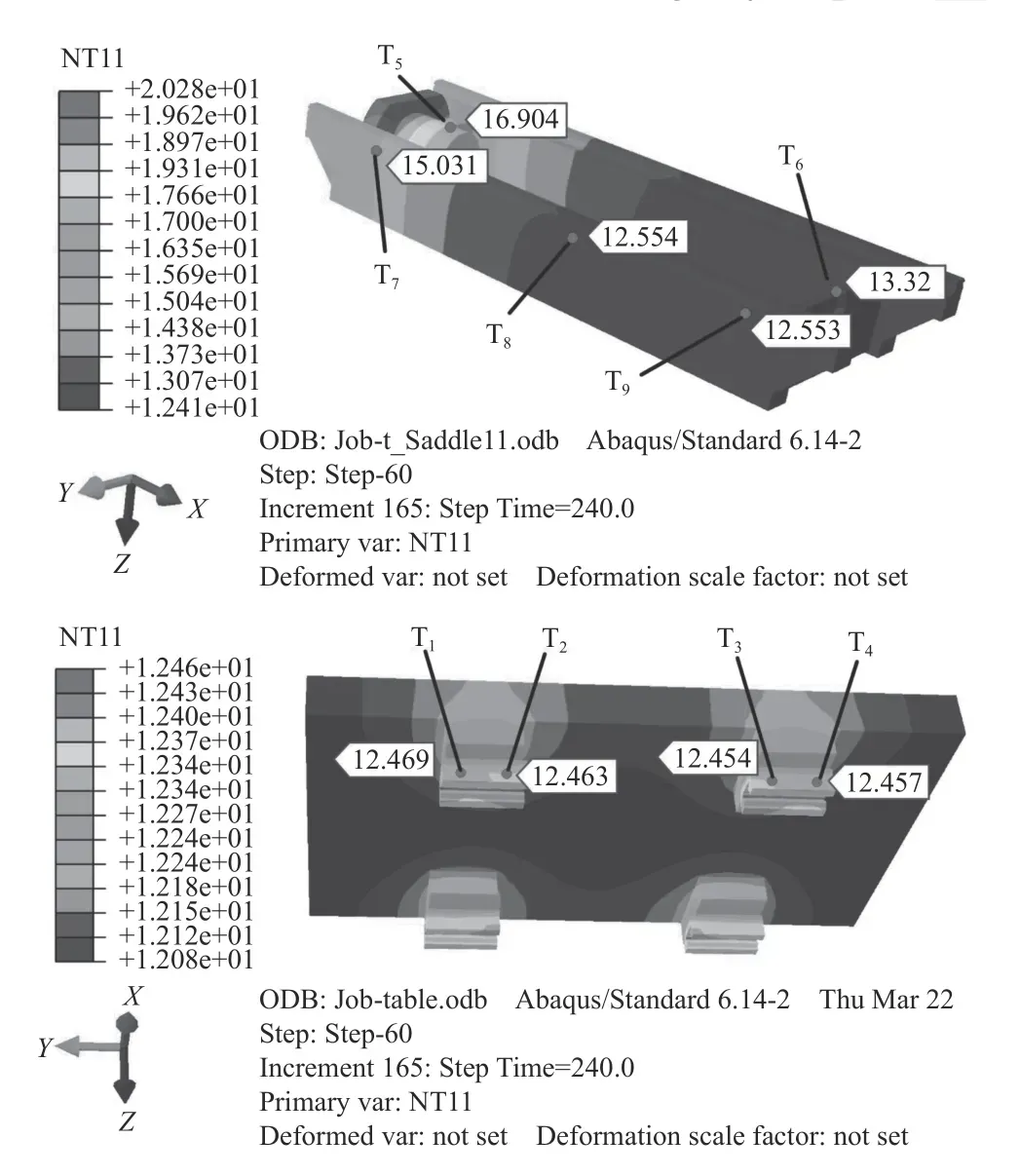
图7 参数化方法计算CHTC热分析结果

4.2.2 结果分析与讨论

在9个温度测点中，T1～T4布置在滑块上，现从两个滑块中分别选择T1和T4，然后将他们与其余5个温度传感器测点位置在传统相似准则法求得的温度、CHTC参数化计算方法求得的温度及实验测量的温度数据进行对比，并给出两种仿真分析结果相对实验数据的仿真误差，如表5所示。

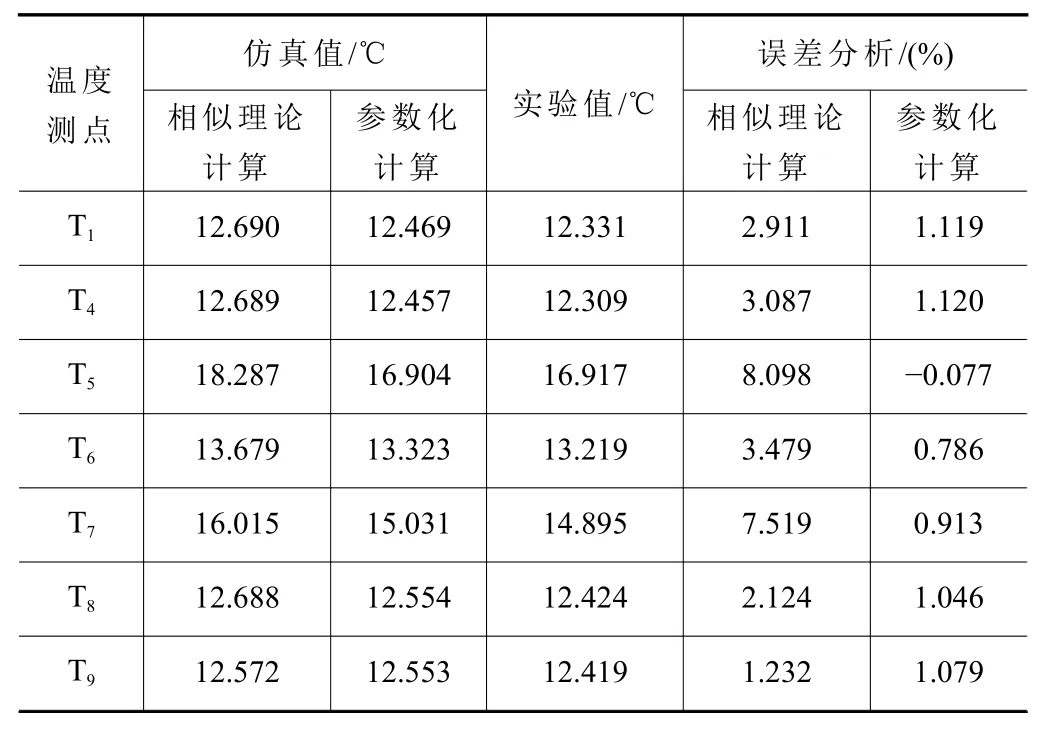
表5 CHTC参数化计算方法与相似准则法的误差分析

从表5中可以看出，参数化计算方法的仿真误差相比传统相似准则法有提高，误差提高幅度最大有8.09%，最小为1.23%，且温升差距越大，迭代方法提高精度越明显。同时参数化计算方法仿真求得的温度数据与实验测值非常接近，说明参数化计算方法具有效性。

5 结语

通过上述分析，验证了文中提出的CHTC参数化计算方法的有效性，并且可得到如下结论：

（1）引入实验数据，通过迭代修正增加了CHTC计算的可靠性与计算精度。

（2）引入温度分区间，在CHTC计算中提出分段修正的计算方法。能够减小机床结构在达到热稳定前，由于环境温度与自身温差的变化对热分析结果的影响。

（3）相比式（1）中的8个未知物理量，CHTC的参数化计算方法更加方便快捷，极大地提升了CHTC和机床结构热分析的计算效率。