基于介电常数近零媒质的舰船隐身材料微波传感器*
唐 艳, 毛雨薇, 周永金
(1.海装上海局驻上海地区第七军事代表室,上海 201108; 2.上海大学 通信与信息工程学院,上海 200444)
0 引 言
当前所有目标特性探测制导手段中,雷达探测制导是致使舰船被远距离攻击的主要威胁之一[1]。材料技术由于具备隐身效果优异、应用条件简单、不受机体外形限制等特点,在舰船雷达波隐身设计中,隐身材料主要作为舰船外形隐身技术的补充手段进行运用[2,3]。为了能够准确进行隐身吸波材料的设计,准确、有效地测量隐身吸波材料的介电常数对舰船雷达波隐身的研究起决定性作用[4]。
测量介电常数法从最原始的电容器测量方法发展到传输线法[5]、谐振腔法[6,7]等。其中,谐振法与其他方法相比,具有准确度高的优点而引起人们的广泛关注。随着超材料逐渐被人们发掘,以开口谐振环(split-ring resonators,SRR)[8]、互补开口谐振环(complementary split ring resonators,CSRR)[9]等平面谐振器为基础设计的微波传感器应用逐渐增多。Shen H T等人提出了一种基于改进型互补谐振环结构的微波传感器,并增加一个压控可变电容二极管来起到频率调谐的作用,用于在多个频率下独立测量介质材料的介电常数和磁导率,测量误差在7 %左右[10]。
近年来,近零媒质超材料作为电磁学领域的一个新兴研究热点,具有许多异于普通媒质的特殊性质。近零煤质超材料包括介电常数近零(epsilon-near-zero,ENZ)媒质、磁导率近零(magnetic conductivity-near-zero,MNZ)媒质、介电常数和磁导率近零(epsilon-and-magnetic conductivity-near->zero,EMNZ)媒质[11]。在近零媒质中传播的电磁波的波长通常远远大于结构本身的尺寸,这使得磁场的相位在这种媒质中均匀分布,而且,在该媒质中折射率和群速度接近于零,波长和相速度接近于无穷大[12],各种能够灵活操控电磁波的新型近零媒质相继被提出[13]。Zhou Z H等人在双辐射端的基片集成波导(substrate integrated waveguide,SIW)中,基于ENZ媒质设计了一种具有极低剖面、辐射模式可重构的天线[14]。
本文提出一种基于ENZ媒质的雷达波隐身材料微波传感器。首先,基于SIW结构设计一种结构简单的ENZ媒质,将隐身吸波材料放置在该媒质的一端或两端,ENZ媒质对隐身吸波材料的变化敏感。仿真结果表明,当隐身吸波材料介电常数实部改变时,ENZ媒质的谐振频率发生明显变化,当隐身吸波材料介电常数虚部改变时,ENZ媒质的谐振强度发生明显变化,因此可以从谐振频率和谐振强度反演得到隐身吸波材料的复介电常数。
1 ENZ媒质
SIW利用金属化通孔阵列在上、下面为金属层的低损耗介质基片上实现传统金属波导的功能。与传统的矩形金属波导相比,SIW不仅具有同样良好的传播特性,还具有体积小、成本低、抗电磁干扰、易于与平面电路集成等特性,所以,由其构成的微波器件及其子系统具有高Q值、高功率等优点[15]。对于TE10传输模式,SIW的有效相对介电常数为
(1)
式中εr为介质基板的相对介电常数,c为真空中的光速,Weff为SIW的等效宽度由式(2)给出[16]
Weff=W-D2/0.95P
(2)
式中W为两列金属通孔的间距,D为金属通孔的直径,P为金属通孔的间距。SIW的截止频率为
(3)
则式(1)可以重写为
(4)
可以看到,当工作在截止频率f0以上时,SIW支持传播波,εeff为正;当工作在截止频率f0以下时,波沿传播方向呈指数衰减,εeff为负。当工作在截止频率f=f0时,在这种临界情况下,SIW内部的场将整体振荡,以零相位的方式沿着传播方向前进,表现为ENZ媒质。
本文所提出的ENZ媒质的三维视图和俯视图分别如图1(a)和(b)所示。介质基板的介电常数为2.65,损耗正切为0.002,厚度H为2 mm。介质基板上方矩形金属贴片长度为L,宽度为W。两列金属通孔沿y轴周期性排列,沿x轴方向的另外两边则是开放的,用于电磁波的辐射。由式(3)计算得到工作频率f0=8.1 GHz。该传感器的具体参数为:W=11.4 mm,L=17.6 mm,P=1 mm,D=0.6 mm。
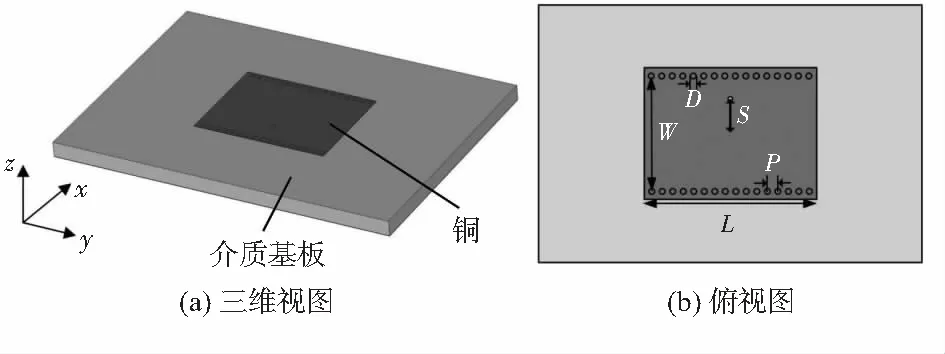
图1 ENZ传感器的结构
该结构由一个距矩形贴片中心偏移距离S的同轴探针进行馈电,通过调整偏移距离来匹配输入阻抗,当S=3 mm时,得到最优的阻抗匹配。利用商业电磁仿真软件CST模拟得到8.1 GHz时的电场分布,如图2所示。可以看出,当工作在截止频率f0以下时,ENZ媒质中的波长是无限的,电场沿SIW的传播方向没有变化。
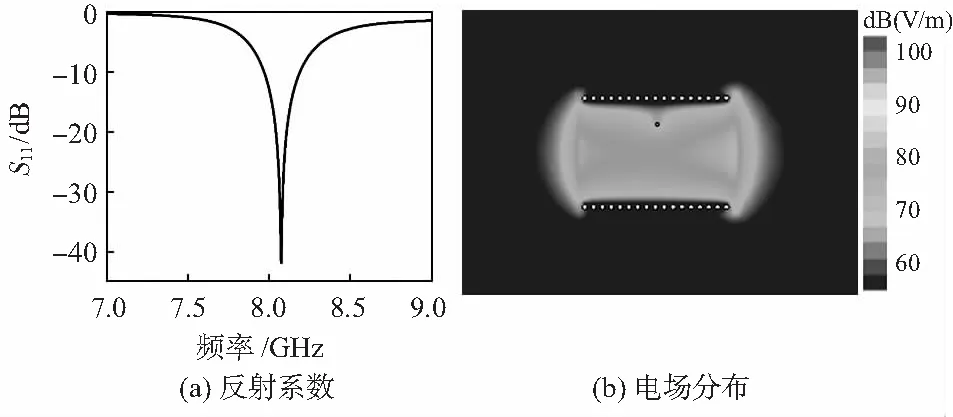
图2 ENZ媒质的仿真结果
2 基于ENZ媒质的隐身吸波材料测量
将隐身吸波材料放置在ENZ媒质的单端进行测量,如图3所示。其中,隐身吸波材料的长度、宽度和高度分别为13.2,1,0.1 mm。在微波范围内,设置常用隐身吸波材料介电常数实部ε′ 的变化范围为4~9,虚部ε″ 的变化范围为0~4.5。由于隐身吸波材料能够显著吸收辐射波,可以预期该结构的S参数对于隐身吸波材料介电常数的变化敏感。

图3 单端加载隐身吸波材料的ENZ媒质传感器
当不同的隐身吸波材料被加载在ENZ媒质传感器的单端时,其S参数如图4(a)和(b)所示。如图4(a)所示,可以看到,随着介电常数的增大,谐振频率逐渐减小;如图4(b)所示,当介电常数实部固定,随着虚部的增大,S11谐振强度减弱,幅值逐渐增大。
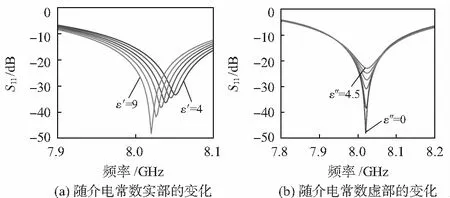
图4 随隐身吸波材料介电常数实部和虚部变化时的反射系数
在隐身吸波材料体积相同的情况下,将其分成均等的两份,分别放置在ENZ媒质传感器的两端,该双端加载隐身吸波材料的ENZ媒质传感器如图5所示。

图5 双端加载隐身吸波材料的ENZ媒质传感器
当不同的隐身吸波材料被加载在ENZ媒质传感器的双端时,其S参数如图6(a)和(b)所示。如图6(a)所示,可以看到,随着介电常数的增大,谐振频率逐渐减小;如图6(b)所示,当介电常数实部固定,随着虚部的增大,S11谐振强度减弱,幅值逐渐增大。与单端加载隐身吸波材料的ENZ媒质传感器相比,由于相同体积的材料受到的辐射场强度增加,导致谐振频率的偏移也增大。
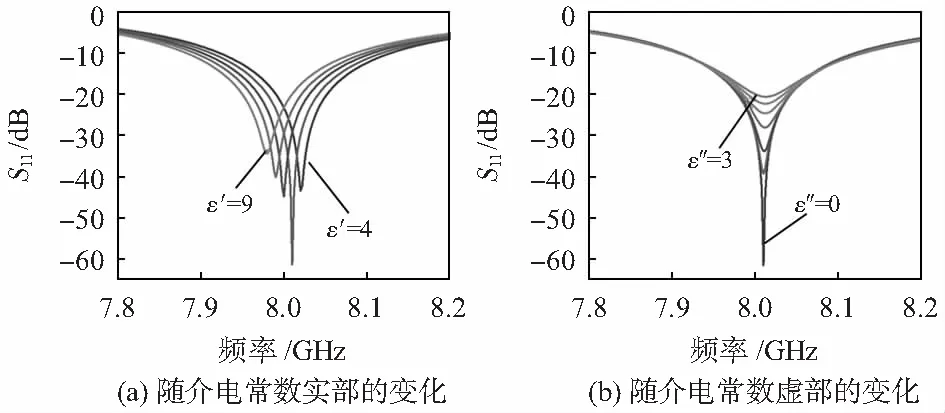
图6 随隐身吸波材料介电常数实部和虚部变化时的反射系数
比较单端加载隐身吸波材料的ENZ媒质传感器和双端加载隐身吸波材料的ENZ媒质传感器的S参数曲线,可以看出,在相同的体积下,采用双端加载测量要比单端加载测量得到的频偏大,有利于提高测量的灵敏度,因此,采用双端加载隐身吸波材料的ENZ媒质传感器。复介电常数与谐振频率、幅值之间的关系,如图7所示的曲线,可以看出,谐振频率随着介电常数实部的增大而减小,谐振幅度随着虚部的增大而增大。

图7 双端加载隐身吸波材料的ENZ媒质传感器的 介电常数与谐振频率、幅度的关系
本文在双端加载隐身吸波材料的ENZ媒质传感器分别加载不同舰载隐身吸波材料,包括Al/钛碳化硅(Ti3SiC2)、MAS涂层、4 %CB/MAS和5 %MWCNTs/MAS,其介电常数实部分别为8.23,3.51,6.05和6.82,虚部分别为5.4,0.2,0.43和1,仿真得到如图8所示的S参数曲线,可以看出,MAS涂层对应的谐振频率最高,Al/Ti3SiC2对应的谐振频率最低,并且Al/Ti3SiC2对应的谐振强度最弱,MAS涂层对应的谐振强度最强。

图8 不同隐身吸波材料对应的反射系数
3 ENZ媒质传感器的参数反演
以介电常数实部为例,根据不同介电常数实部对应的谐振频点,利用MATLAB中的曲线拟合工具,可以得到隐身吸波材料介电常数实部与谐振频率的拟合方程为
y=266.8×sin(x-3.14)+34.48(x-10)2+133
(5)
式中x为谐振频点,y为反演的隐身吸波材料介电常数实部。
将图8中从不同舰载隐身吸波材料的反射系数得到的频率代入式(5),反演得到这些材料的介电常数实部,并与参考的介电常数实部进行对比。为了量化测量误差,将其定义为
(6)
式中εs为参考介电常数实部,εf为反演介电常数实部。材料的介电常数实部测量值、谐振频率、虚部、谐振幅值以及误差如表1所示。结果表明,所得介电常数与参考值之间的误差较小,测量误差在2.26 %以内。

表1 不同隐身吸波材料的复介电常数反演
4 结 论
设计了一种单端加载隐身吸波材料的ENZ媒质传感器和一种双端加载隐身吸波材料的ENZ媒质传感器来测量隐身吸波材料的复介电常数。双端加载隐身吸波材料的ENZ媒质传感器具有更高的灵敏度,通过在双端加载不同常用舰载隐身吸波材料,获得其谐振频率和谐振强度,进一步反演得到复介电常数实部和虚部,仿真结果与实验参考数据吻合良好,验证了该传感器的有效性和准确性。

