享受思维“冲浪”逐层认识“全等”

文／姜鸿雁

经过七年级的学习，同学们一定对一些平面几何图形有了初步认识，比如线段、角、三角形、平行线等，也初步明白了几何研究的对象是图形，知道了既要研究图形的定义、性质、判定和应用，还要研究图形与图形之间的数量关系、位置关系等。这些是几何学习的“原材料”。我们在发现全等、证明全等、应用全等、图形变换、构造全等的思维冲浪过程中，将逐步深入认识全等三角形。

一、发现全等——识图能力的考验

识图能力的培养从我们进入几何大门的那一刻便已开始。全等三角形的学习，对同学们识图能力的要求随之提高。例如，如图1，点C在线段AB上，且CE=CA，CF=CB，∠ACE=∠FCB=60°，连接AF、BE相交于点P，分别交CE、CF于点M、N。

图1

同学们能看出图中有几对全等三角形吗？怎样识图不易遗漏呢？首先，我们要会给线段或角找到“家”，也就是一条线段或一个角是哪个或哪些三角形中的元素。比如，线段AC既在△ACE中，还在△ACF、△ACM中；∠1既在△ACF中，又在△ACM中。其次，要关注“深藏”的等角或等边。比如，本题中“藏着”的∠ACE=∠MCN=∠FCB=60°。最后，你一定遇到过公共角、对顶角、直角（都相等）、公共边、线段中点（平分线段）等这些全等的“自然资源”吧？

识图不仅在数学内部，对生活中的一些现象，也要能抽象成数学图形。比如，在生活中，我们常常看到人们用大拇指指尖和中指指尖测量两点间的距离，这个距离叫作“拃”（如图2）。你看到其中的几何图形了吗？同学们要慢慢学会用数学的眼光看世界。

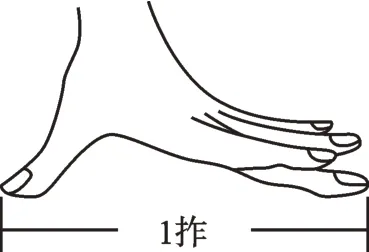
图2

二、证明全等——推理能力的提升

欧几里得的巨著《几何原本》，是从五个公理出发，通过一个个严密的推理建成几何的大厦，体现了推理的力量，彰显了数学的理性。因此，仅在复杂的图形中发现全等三角形还不够，我们还需要运用全等三角形的判定方法（SAS、ASA、AAS、SSS、HL）加以证明，才具有说服力。例如，在图1中，用“SAS”证得△ACF≌△ECB，由它生发的∠1=∠2是△ACF≌△ECB的一个性质，也是△ACM≌△ECN的判定条件之一，其他全等三角形的证明也水到渠成。

生活中，人们为什么能用“拃”测量两点之间的距离呢？看了图3，相信你一定会恍然大悟！学习是“知其然，知其所以然”的过程，同学们要慢慢学会用数学的思维思考世界。

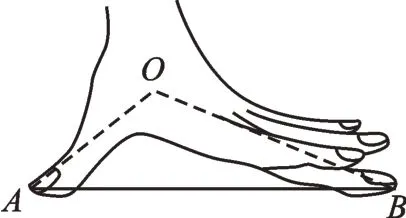
图3

三、应用全等——应用意识的觉醒

全等三角形的对应边相等、对应角相等、面积相等……这些性质是证明两条线段相等、两个角相等的有力“武器”，同时，也是进一步学习其他重要几何定理的保障。例如，在图1中，只有先由△ACF≌△ECB证得∠1=∠2，才能证明△ACM≌△ECN。本题还可以通过求∠EPA证明CM=CN，动手试试，相信你一定行！

根据图1中的已知条件，结合小学的经验，你一定能猜到△ACE、△CBF是等边三角形。但是它们为什么是等边三角形？依据什么定理？未来，同学们将以全等三角形为依托，学习与等边三角形有关的定理，所以说，全等三角形是几何大厦中的一块重要的“奠基石”。

在实际生活中，全等三角形也有广泛的运用。同学们要慢慢学会用数学的“语言”（比如，图形及图形之间的关系）表达世界。

四、图形变换——静中见动的智慧

平移、翻折、旋转改变的是图形的位置，不变的是形状与大小，变换前后的两个图形全等。因此，我们看到的一对对全等三角形是静止的，但也是灵动的。

例如，在图1中，CA、CE是等边△ACE的两条边。我们既可以把CA看成绕点C顺时针旋转60°，得到CE，也可以把△ACF看成绕着点C顺时针旋转60°，得到△ECB。你还能看出其他全等三角形的变换方式吗？以后我们还将学习以平面直角坐标系为依托，从“数”的角度刻画“形”的变换。

未来，我们还要学习只改变图形大小，不改变图形形状的变换——相似变换。例如，在图1中，我们可以认为等边△ACE是绕着点C顺时针旋转120°，并按一定比例缩小得到等边△FCB。全等是相似的特例，学好全等可以为未来学习相似奠定基础。

五、构造全等——从无到有的创见

再看图1，连接PC，你能证明PC平分∠APB吗？显然∠APC、∠BPC无论放在哪两个三角形中，都没有全等，怎么办？构造全等！如图4，作CH⊥AF、CG⊥BE，垂足分别为H、G。CH、CG还可以看成△ACF、△ECB对应边AF、BE上的高（又是识图能力的考验），相信同学们一定能想到用“HL”证明Rt△PHC≌Rt△PGC。因此，构造全等是基于对已知条件、待求目标以及全等变换等因素综合分析的结果。

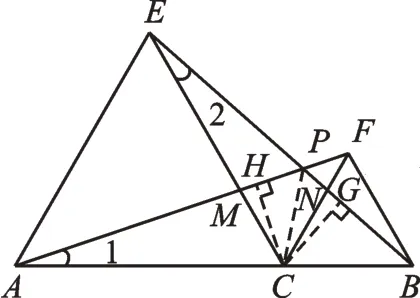
图4

发现、证明、应用、变换、构造，由浅到深的思维历程不仅仅是我们学习全等三角形所要经历的，也是认识、研究其他几何图形需要经历的。同学们，你们将从全等三角形这章开始，插上几何学习腾飞的翅膀！