二阶电报方程的一个新紧差分格式
李福乐,秦墩旺,刘振斌,徐英
(青岛农业大学理学与信息科学学院,山东青岛 266109)
考虑下列方程组:
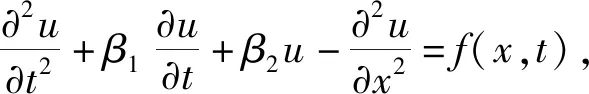
(1)
(2)
u(0,t)=h1(t),u(1,t)=h2(t),0 (3) 式(1)称为电报方程或传输线方程,可用来描述输电线路中的电信号、色散波传播、动脉内的脉动血流和树篱上虫子的随机运动等一系列物理和生物现象[1];式(2)、式(3)分别为初始条件和边值条件,其中u表示电压,x、t分别为距离和时间,β1、β2为正常数,f、g1、g2、h1、h2为已知函数。对于上述电报方程,学者使用多种方法进行了研究,其中有限差分法[1-3]、DGJ方法[4]、有限元法[5]、样条方法[6-9]、再生核方法[10]等被广泛应用于数值解求解。文献[10]给出了变系数电报方程的一个紧差分格式,但未给出其理论分析结果。本文对(1)~(3)建立了一个线性三层紧差分格式,紧差分格式的收敛阶可以达到O(τ2+h4)。 (4) 由带积分余项的泰勒公式得 (5) (6) (7) (8) 其中 将(5)~(8)代入(4),得 (9) 在(9)式两边作用算子A,得 又 其中 由此得到 (10) 对于初始条件,通过类似的推导可以得到: (11) (12) (13) (14) (15) 虽然式(11)的局部截断误差仅为O(τ+h4),但可以证明差分格式(12)~(15)整体的收敛阶能达到O(τ2+h4)。 用能量分析法可得到如下先验估计[11]。 1≤i≤m-1,1≤k≤n-1 进一步还可以得到 由引理1容易得到关于差分格式解的可解性、稳定性和收敛性结论。 定理1紧差分格式(12)~(15)是唯一可解的。 定理2紧差分格式(12)~(15)的解关于初值和非齐次项在L∞范数下是无条件稳定的。 则有‖ek‖∞=O(τ2+h4)。 下面给出具体算例来验证紧差分格式(12)~(15)的有效性。取T=1,β1=20,β2=25,精确解u=e2tsin(πx)。相应的非齐次项f及初边值条件由(1)~(3)给出。分别取m=10、20、40、80、160,n=m2/20。定义最大误差 所得结果见表1至表3。图1给出了u(x,t)的数值解曲面,图2给出了t=1时不同步长数值解的误差曲线。 图1 数值解曲面Fig.1 Surface of the numerical solutions 图2 不同步长数值解的误差曲线Fig.2 Error curves of the numerical solutions with different step size 表1 不同网格数部分点处的数值解Table 1 Numerical solutions at partial points for different grid number 由表2可以看出,当h缩小至原来的1/2时,误差约缩小至原来的1/16。利用表3中的数据可以得到如下线性拟合函数: -lnE∞(h,τ)≈-8.149 8+3.991 4(-lnh) 表2 不同网格数部分点处的绝对误差Table 2 Absolute errors at partial points for different grid number 表3 不同网格数数值解的收敛阶和最大误差Table 3 Convergence orders and maximum errors of the numerical solutions for different grid number 由此看出,紧差分格式(12)~(15)的收敛阶可以达到O(τ2+h4),与理论结果相符。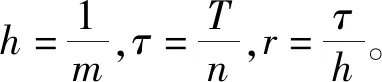
1 紧差分格式的建立及截断误差表达式
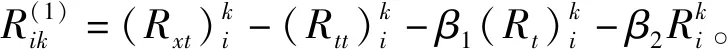

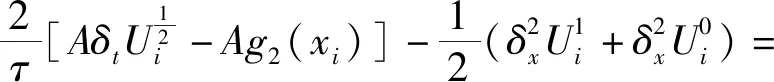


2 紧差分格式的理论分析



3 数值模拟






