基于LS-SVM的第一类积分方程的近似解法

曹秀梅，朱明月，吴自库

(青岛农业大学理学与信息科学学院，山东青岛 266109)

很多力学、工程等学科中的问题都可以归结为积分方程，例如电磁问题[1]、位势问题[2]。近年来，无论在理论上[3]，还是在数值解法上[4]，对积分方程的研究都取得了丰硕的成果。就数值解而言，一些新方法被不断推出，如Hermite配置方法[5]、互补解法[6]、谱正则化方法[7]等。但由于积分方程本身的复杂性，特别是第一类积分方程的突出特性——不适定性[8-9]，导致第一类积分方程的求解存在很多困难，因此探讨第一类积分方程的数值解法成为学者的一个研究方向。一些学者尝试利用机器学习方法求解积分方程，人工神经网络方法是采用较多的一种[10-11]，但该方法的两个缺点(隐含层数难确定、容易陷入局部极小值)对克服第一类积分方程的不适定性不利。最小二乘支持向量机(least squares support vector machine，LS-SVM)[12]能较好地克服这两个缺点，并已成功地应用于解微分方程及其反问题[13-16]。LS-SVM作为一种机器学习方法，在求解积分方程方面的研究还不是很多，尤其在求解第一类积分方程方面。本文尝试将该方法用于求解第一类Volterra和Fredholm积分方程。

1 解法机制

1.1 基于LS-SVM的第一类Volterra积分方程的解法机制

研究如下形式的第一类Volterra积分方程：

(1)

(2)

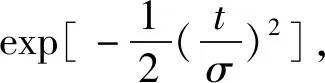
利用复化梯形求积公式，将式(2)代入到方程(1)有：

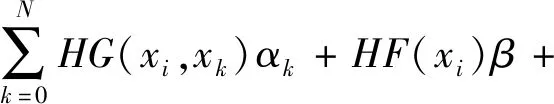
(3)

这里

为引入的偏差。

根据LS-SVM原理可将参数估计问题转换为如下的二次规划问题进行求解：

(4)

其中γ为正则化因子。二次规划问题(4)可通过拉格朗日乘子法求解，引入拉格朗日乘子μT=[μ0,μ1,μ2,…,μN]，拉格朗日函数为：

(5)

由Karush-Kuhn-Tucker(KKT)条件可以得到如下方程组：

(6)

其中N1=N+1；D11=IN1(N1阶单位矩阵

D33=(0)1×1；Z=(0)N1×1，U=[-η·g(xi)]N1×1。

定理1：在给定可调参数σ和γ条件下，方程组(6)有唯一解。

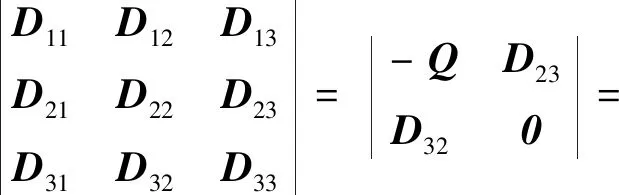
(7)

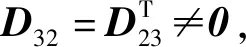
1.2 基于LS-SVM的第一类Fredholm积分方程的解法机制

研究如下形式的第一类Fredholm积分方程：

(8)

方程(8)同方程(1)区别在于方程(8)上限为常数，因而与第一类Volterra积分方程相比，其解法机制并没有本质区别。采用复化Simpson求积公式对定积分部分进行数值积分。将区间[a,b]进行N=2M等分，步长

xk=a+k·h1，则复化Simpson求积公式如下：

未知函数f(x)仍然取公式(2)的形式，最终可以将参数估计问题转化为如下形式的二次规划问题：

(9)

这里

其他符号的意义同1.1节。则二次规划问题(9)的拉格朗日函数为：

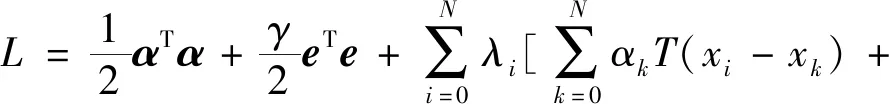
(10)

由拉格朗日乘子法，二次规划问题(9)为如下方程组的解：

(11)

其中

C23=[F(xi)]N1×1；C31=(0)1×N1，C32=[F(xi)]1×N1，C33=(0)1×1；Z=(0)N1×1，U=[-η·g(xi)]N1×1。

定理2：在给定可调参数σ和γ条件下，方程组(11)有唯一解。

方程组(6)和(11)形式上完全一样，可以统一为AX=B。在实际应用中为了增加稳定性，可以改写为：

[ATA+εI]X=ATB

(12)

当ε→0+时收敛于原问题的解。之所以采用公式(12)的形式，是为了避免方程组病态。

2 数值算例

为验证本文算法的有效性，选取4个数值例子。为便于比较，4个数值例子均取自文献[17-19]。将积分区间[a,b]100等分，101个节点为训练点集；再将积分区间150等分，151个节点为测试样本点。选取最大误差和均方根误差为比较指标。考虑到正则化因子γ的作用，取为常数(1.0×108)，因而核宽度参数σ是唯一可调参数，这是本方法的优点之一。具体数值算例如下。

数值算例的数值结果见表1，图1是对应的解析解与数值解误差曲线。从数值结果来看，本方法用于数值求解第一类积分方程完全可行，达到或超过了原文献的精度。此外，本方法克服了问题的不适定性，数值解稳定，而且是闭式解析解。

表1 数值结果Table 1 Numerical results

3 结论

积分方程数值解法是积分方程领域的研究热点之一，然而基于机器学习理论的积分方程数值解法尚不多见。本文成功地将LS-SVM方法用于解第一类线性积分方程，在理论上给出了解法机制，数值结果表明本方法可行且具有较高的精度。下一步，如何求解其他类型的积分方程尤其是非线性积分方程，是本方法的重要研究方向。

A.例1；B.例2；C.例3；D.例4。图1 数值解的误差曲线Fig.1 The error curves of numerical solution