基于重庆岩层的复合式TBM刀盘中心滚刀布置形式及受荷规律研究
汪 平,张康健,李 进,张志强,李小伟
(1.重庆交通建设(集团)有限责任公司,重庆 400010; 2.西南交通大学交通隧道工程教育部重点实验室,成都 610031; 3.重庆建筑工程职业学院,重庆 400072)
引言
目前,全断面岩石掘进机(TBM)越来越广泛应用于隧道工程的全断面机械化开挖[1]。刀盘上的刀具布置直接影响TBM掘进效率和隧道建设工期,因此,刀具布置设计常常成为TBM刀盘设计的核心[2]。中心滚刀位于刀盘的中心部位,常常为双刃滚刀,其公转直径相对较小,破岩时刀刃在岩面上的径向滑移较大[3-5]。掘进过程中由于中心滚刀工作环境恶劣,受力复杂,一旦发生故障,极易出现刀圈偏磨甚至轴承发生损坏[6-7]。因此,研究中心滚刀的受力特征和优化布置,对提高TBM的掘进性能和施工效率具有重要意义。
一些学者对滚刀受荷规律和优化布置等进行了研究,取得了一定的研究成果[8-11]。暨智勇等[12]建立了单把滚刀受载力矩模型和刀盘倾覆力矩模型;张旭辉等[13]基于颗粒离散元法,分析了间距与围压等因素对中心双刃滚刀破岩特性的影响;苏鹏程等[14]从刀盘受力空间力系平衡的角度对滚刀进行了优化;周阳宗等[15]对复合刀盘进行校核后利用遗传算法优化刀具的布置;刘建琴等[16-17]基于滚刀受力模型构建了刀盘载荷描述方程,提出了正滚刀极径设计方法;孙金山等[18]研究了单双刃滚刀作用下岩石内部应力和裂纹扩展的差别;张魁等[19]提出TBM刀具作用下岩石存在4种基本的破碎模式;谭青等[20]研究了滚刀结构参数、受荷特征及岩石破碎特性的规律。
上述研究成果对于探究滚刀破岩机理及指导滚刀优化布置具有重要的参考价值,但现有研究多集中于单刃滚刀,而对中心双刃滚刀研究较欠缺。中心滚刀公转直径较小,且双刃的设计方式也使得其破岩机制和受力特征明显不同于单刃滚刀。刀盘上中心滚刀的布置形式通常为“一”字形和“十”字形,目前不同布置形式下中心双刃滚刀的受荷规律差异也尚不明晰。因此,有必要对中心双刃滚刀的受荷规律和布置形式进行研究。
考虑到离散元颗粒流可根据颗粒间接触的变化来自动生成宏观本构关系,表现出复杂的力学行为,能够较好地模拟大变形、裂缝发展、断裂等问题,基于颗粒离散元法,建立中心滚刀群与围岩的相互作用模型,模拟复合式TBM掘进过程中中心双刃滚刀的破岩过程,研究了中心双刃滚刀的受荷规律和布置形式,为刀盘上刀具的合理布置提供依据,保证TBM顺利高效掘进。
1 依托工程概况
重庆市轨道交通环线南桥寺站—体育公园站区间全长722.6 m、体育公园站—冉家坝站区间全长902.7 m,均为暗挖隧道。考虑到隧道所经地层的具体条件和TBM的地质适应性等因素,采用复合式TBM进行区间隧道掘进开挖。复合式TBM基于土压平衡盾构的原理,发展了土压平衡盾构的优点,通过模式转换使其能够在软弱富水土层及软硬交互地层高效掘进。当在微风化岩层或掌子面稳定性较好时,复合式TBM采用敞开模式进行掘进;当岩土体较软弱、节理裂隙较发育、地下水较丰富时,复合式TBM采用土压平衡模式进行掘进以保证开挖面的稳定。
以该区段为工程依托,研究了岩质条件下复合式TBM中心滚刀的受荷规律和布置形式,以期为复合式TBM刀盘上刀具的合理设计提供参考。图1为该区段使用的TBM刀盘上滚刀布置。
2 接触模型选取及岩石细观参数标定
离散元颗粒流在生成模型时不能直接为研究对象的宏观物理力学参数赋值,而是通过模型的细观力学参数和颗粒接触模型来生成与物理试验结果相近的宏观物理参数和本构关系。目前,材料的宏观物理性能与细观参数间的相关关系仍不明确,比较通用的做法是先假定一套粗糙的微观参数,通过单轴压缩试验、巴西劈裂试验或三轴压缩试验等数值试验,不断调整微观参数,使颗粒集合体表现出的宏观特性能够匹配材料真实的宏观特性,通过这种方法来建立颗粒微观参数和材料宏观特性之间的联系。
PFC平行黏结模型中相互作用的颗粒间可传递法向力、切向力和力矩,可模拟颗粒集合体的黏结损伤效应,较好地模拟实际岩石材料。接触黏结模型仅通过颗粒间的接触点传递力,不能模拟颗粒间力传递的不均匀性,无法模拟粒子在外力作用下的损伤效应。因此,采用平行黏结模型作为颗粒间的接触模型。

图1 TBM刀盘上滚刀布置
以重庆地区典型砂岩为试验对象,通过巴西劈裂、单轴压缩等实验室试验,并结合工程地勘报告确定其宏观物理力学参数,如表1所示。

表1 岩石宏观力学参数
采用PFC3D软件,建立尺寸分别为φ50 mm×100 mm(h)和φ50 mm×50 mm(h)的圆柱体颗粒试样模型,进行砂岩细观参数的数值标定试验(图2)。经过多次细观参数数值标定试验,反复调整颗粒流模型的细观参数,得到与实际岩石物理力学参数相匹配的颗粒流模型细观参数(表2),相应的颗粒集合体所表现出的宏观力学特性如表3所示。

图2 数值标定试验

表2 三维颗粒流模型细观参数
由于平行黏结相互作用模型有其自身的局限性,用其表征的材料无法同时满足抗拉强度和抗压强度,故采用弹性模量、泊松比、抗压强度、黏聚力和内摩擦角作为宏细观参数的匹配指标。对比表1和表3可以看出,采用表2的颗粒流细观参数所模拟出的岩样宏观参数与砂岩真实宏观参数间的差别较小,因此,可以认为该套细观参数能够模拟岩石的宏观力学特性,在后文的滚刀破岩模型中均采用该组颗粒流细观参数。

表3 三维颗粒流模型宏观力学参数
3 模型设置及刀盘总荷载分析
中心滚刀在刀盘上的布置方式可分为“一”字形和“十”字形两种。本节以这两种典型布置方式为例,研究中心滚刀不同布置方式对刀盘中心滚刀受力的影响,模型尺寸如图3所示。假设滚刀为刚体,不考虑滚刀-岩石作用过程中的磨损和变形,滚刀尺寸如图4所示。

图3 模型尺寸示意 (单位:mm)

图4 滚刀尺寸 (单位:mm)
滚刀公转的同时在摩擦力作用下自转,根据现场TBM掘进参数资料,滚刀群顺时针旋转,绕刀盘中心公转转速取为5 r/min,掘进速度为0.417 mm/s,在整个破岩模拟过程中,通过伺服机制建立边界wall的运动和围压之间的关系,实时调整边界wall的运动即可使围压保持不变。考虑本工程区间隧道埋深在20~30 m,使用刚性边界条件仅在岩石颗粒模型圆形周边上施加500 kPa围压。最终建立颗粒流模型如图5所示,模型中岩石颗粒Rmax/Rmin取1.66,颗粒孔隙率取0.2。

注:图中滚刀按安装半径由小到大的顺序进行编号。图5 中心滚刀数值模拟颗粒流模型
在实际盾构掘进中,滚刀并非是在平整岩面上进行掘削破岩,考虑岩石破碎环境对结果的影响,中心滚刀群掘削2圈使岩面产生初始破碎后再通过PFC3D中“history”命令对各滚刀所受垂直力、滚动力和侧向力进行监测,并对监测数据进行处理,获得中心滚刀区域刀盘的推力、扭矩、倾覆力矩和不平衡力。
以刀盘旋转中心为基点,建立刀盘空间直角坐标系,刀盘上滚刀受力示意如图6所示。为简化分析,不考虑TBM掘进过程中刀盘受到的各种摩擦力和摩擦力矩,定义刀盘推力和刀盘扭矩分别为推动刀具破岩所需的合力和合力矩,即有效推力和有效扭矩。所有滚刀力的合力即为刀盘推力、扭矩、倾覆力矩和不平衡力。
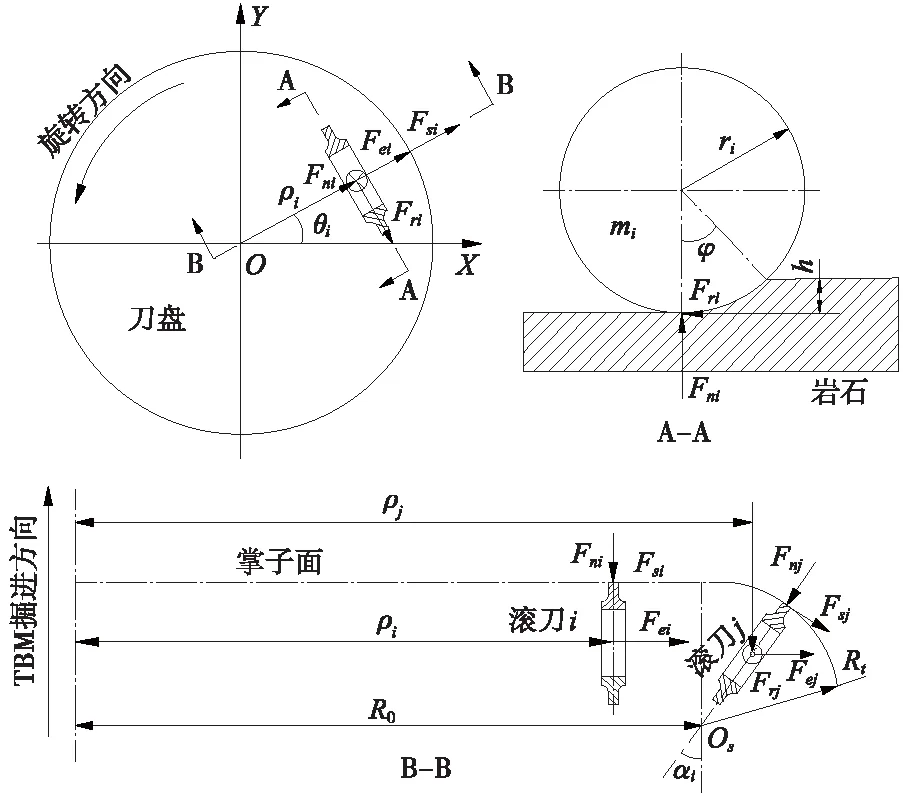
注:表示Fni垂直于纸面向里;表示Frj垂直于纸面向外。图6 刀盘上滚刀受力示意
盘形滚刀在刀盘上的位置可表示为(ρi,θi),其中,ρi为滚刀的安装半径(滚刀中心到刀盘旋转轴线的距离),ρi∈[0,2π]为滚刀的安装极角。由于边缘滚刀位于刀盘的过渡圆弧上,引入αi来描述边缘滚刀的安装倾角,αi∈[0,π/2]。

(1)
式中,Rt为刀盘过渡圆弧半径;ri为滚刀半径;R0为过渡圆弧圆心到刀盘旋转轴线的距离。
TBM掘进过程中,刀盘上的滚刀不仅绕自身轴线自转,还绕刀盘轴线公转,滚刀还受到牵连惯性力Fei和科氏惯性力偶矩Mi的作用,其中,牵连惯性力Fei沿滚刀中心轨迹圆的法线方向,且交汇于刀盘旋转轴线。其计算公式分别如式(2)、式(3)所示。
Fei=miω2ρi
(2)

(3)
式中,Fei为滚刀牵连惯性力;Mi为滚刀科氏惯性力偶矩;ω为刀盘转速;mi为滚刀质量。
刀盘推力和扭矩计算如式(4)、式(5)所示。

(4)
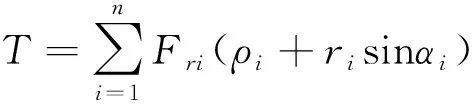
(5)
刀盘不平衡力和倾覆力矩计算如式(6)、式(7)所示。

(6)

(7)
式中,n为滚刀数量;Fx和Fy分别为刀盘x、y方向的不平衡力;Mx和My分别为刀盘x、y方向的倾覆力矩;Fxy和Mxy分别为刀盘不平衡力合力、倾覆合力矩。
4 模型设置及刀盘总荷载分析
考虑到滚刀受到的三向力是不断变化的,故分析中仅考虑整个滚压过程中的三向力均值。三向力均值的计算方法是对整个滚刀滚压过程中系统采集到的三向力数据点取平均作为三向力均值。图7为不同布置方式下中心滚刀的三向力均值,通过式(4)~式(7)可计算并绘制出不同布置方式下中心滚刀区域刀盘的推力、扭矩、倾覆力矩和不平衡力变化曲线,分别如图8、图9所示。

图7 不同布置方式中心滚刀三向力均值
从图7~图9可得到以下结论。
(1)滚刀破岩时,滚刀三向力、刀盘推力、扭矩、倾覆力矩和不平衡力均呈现稳态波动趋势,表明滚刀破岩时岩石发生跃进破碎,这是由岩石材料物理力学性能决定的。随着刀盘的旋转推进,滚刀受力随着侵入岩石深度的增大而增加,当这种相互作用力达到一定值时,下方岩体无法继续承受荷载而发生脆性破坏,刀具荷载大幅下降,其受力呈现阶跃变化的特点。
(2)对比不同安装半径的滚刀受力可以发现,随着安装半径增加,两种布置方式下滚刀垂直力均值和滚动力均值整体均呈增大趋势,而侧向力均值变化并不明显。如1号刀圈垂直力均值为2.43 kN,3号刀圈垂直力均值为11.7 kN,垂直力均值增幅度达3.8倍,同理滚动力均值增幅达2.6倍。随着安装半径增加,刀刃的线速度逐渐增大,在刀盘外侧工作的刀具,破岩量也随之增加。由于所有滚刀随刀盘同步转动,单位时间内外侧刀具比内侧刀具破岩耗能更多,因此,垂直力和滚动力相应会增大。另一方面,越靠近刀盘中心处的岩石越容易产生过度破碎,前期的两圈掘进可能使得不同刀圈之间的侧向裂纹发展较完全,从而导致侧向力均值变化并不明显。
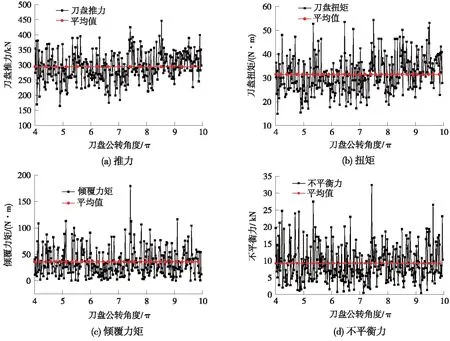
图8 滚刀“一”字形布置刀盘受力
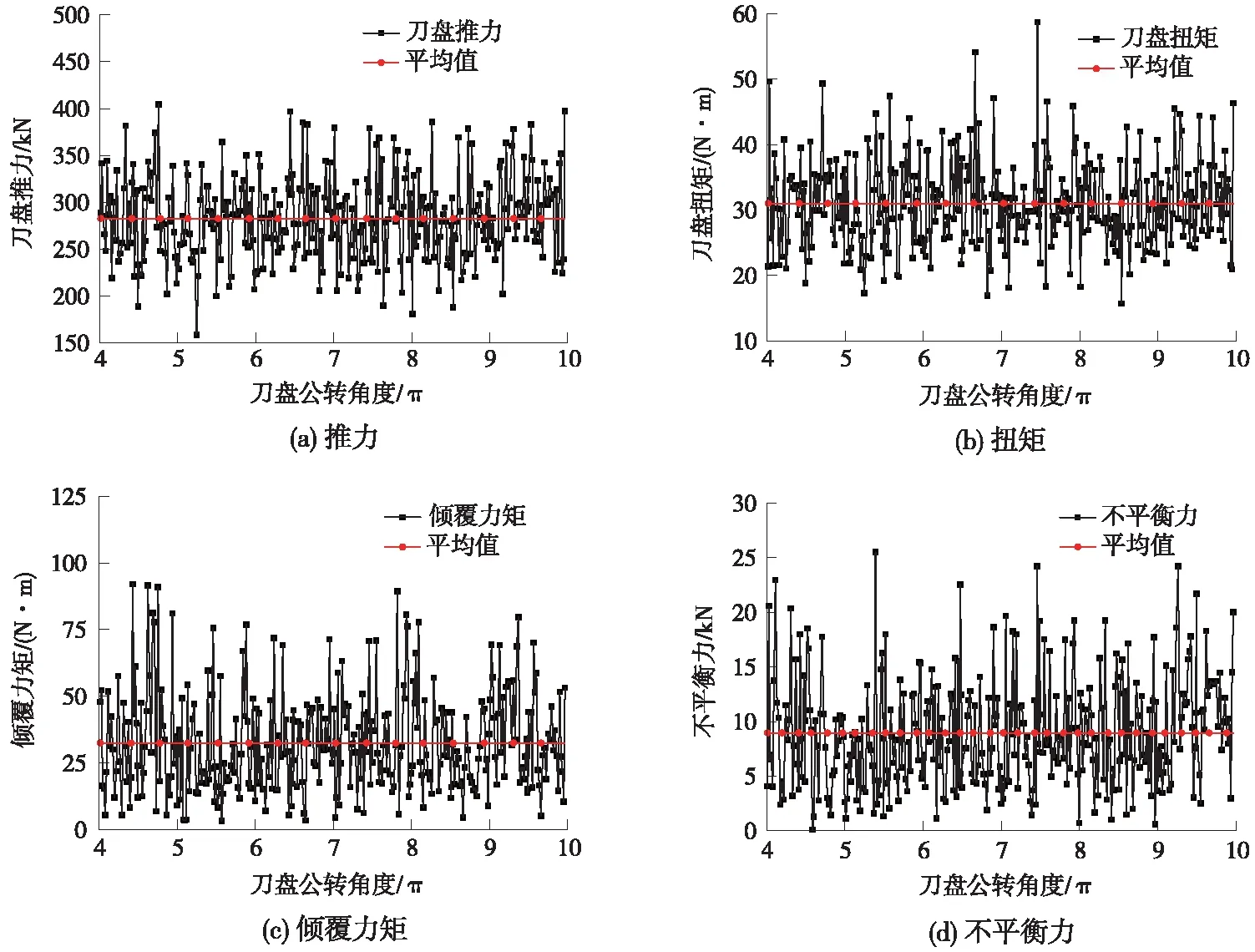
图9 滚刀“十”字形布置刀盘受力
(3)当滚刀安装半径较小时,双刃滚刀内外侧刀圈三向力差异显著,内侧刀圈受力明显小于外侧刀圈,通常这种内外侧刀圈的不平衡受力加剧了双刃滚刀的不均衡磨损,但由于其受荷量值较小,在实际中这种内外刀圈的受荷差异并不会对滚刀磨损产生较为严重的危害。同时,随着安装半径增加,双刃滚刀内外侧刀圈受力差异性逐渐降低,表明安装半径的增加会减弱双刃滚刀内外侧刀圈的受荷差异。
(4)两种布置方式下,滚刀的荷载变化范围随安装半径增加整体上呈现变大趋势,这种高频率高幅度的振荡,致使滚刀越来越处于不利的工作状态。
(5)中心滚刀区域刀盘整体力学特征与滚刀破岩时的三向力密切相关,刀盘的推力、扭矩、倾覆力矩和不平衡力并未出现突变,均在一定范围内波动,呈现稳态波动特征。
对比分析“一”字形和“十”字形两种布置方式下滚刀刀圈和中心滚刀区域刀盘的受力特征,得到以下结论。
(1)当滚刀安装半径相同时,相较于“一”字形中心滚刀布置方式,“十”字形布置可降低单一刀圈的受力和受荷波动范围,有利于降低滚刀磨损。
(2)“十”字形布置方式可降低中心滚刀区域刀盘的整体受力,刀盘倾覆力矩、不平衡力、推力、扭矩分别减少9.60%、2.92%、4.56%、1.65%。从刀盘整体受力平衡的角度来看,“十”字形中心滚刀布置方式更有利于TBM掘进时的稳定,对精确控制掘进方向、降低滚刀破损和提高刀盘的使用寿命具有重要意义。
图10为不同布置方案下岩石的裂纹分布。这两种布置方式下,拉剪裂纹的数目基本相同,相邻滚刀间的裂纹完全贯通,岩渣剥落较完全,这表明中心滚刀的布置方式未对岩石裂纹扩展产生较大影响。

图10 不同布置方式下岩石裂纹分布
5 结论与建议
基于颗粒离散元计算方法,建立了中心滚刀群与围岩的相互作用模型,模拟了TBM掘进过程中中心双刃滚刀的破岩过程,从单一滚刀受力特征、中心滚刀区域刀盘整体力学性能以及岩石裂纹扩展等方面,研究了中心滚刀的受荷规律和不同布置形式产生的差异,得出以下结论。
(1)随着安装半径增加,中心双刃滚刀的垂直力和滚动力整体上呈增大趋势,而侧向力变化并不明显。
(2)当滚刀安装半径较小时,双刃滚刀内外侧刀圈三向力差异显著,内侧刀圈受力明显小于外侧刀圈,安装半径增加则会削弱双刃滚刀内外侧刀圈的受荷差异。
(3)当滚刀安装半径相同时,“十”字形布置可降低单一刀圈的受力,也可以降低中心滚刀区域刀盘的整体受荷,减少刀盘倾覆力矩和不平衡力,有利于TBM掘进时的稳定。
(4)中心滚刀的布置方式未对岩石裂纹扩展产生较大影响,综合考虑掘进效率、施工成本等因素,建议岩质地层复合式TBM中心双刃滚刀采用“十”字形布置方式。

