一维海森堡-伊辛自旋链模型中的量子失协研究

张 乐，袁训锋，雷 健，谭小东

（商洛学院 电子信息与电气工程学院，商洛 726000）

量子失协包括量子体系中的纠缠量子关联和非纠缠量子关联， 而量子纠缠是量子通信与量子计算的重要资源［1］。 作为一种非局域关联，量子纠缠是量子通信区别于经典通信的重要特征， 人们借助量子纠缠能够完成在经典领域中无法完成的工作， 如量子遥传和量子密钥分发等［1］。 人们曾认为量子纠缠是量子信息技术超越其他经典技术的根本原因，但近期的研究结果表明， 量子关联可能比量子纠缠更基础、更广泛［2］。 量子关联包括纠缠关联和非纠缠关联，也就是说，纠缠只是一种特殊的量子关联。 从理论上讲， 非纠缠量子关联可以帮助人们确定量子计算 加 速DQC1 方 案［3-4］和 寻 找 量 子 搜 索 算 法［5-6］，目前，非纠缠量子关联已通过实验［7］得到验证。 2001年，H. OLLIVIER 等［8］通过引入量子失协度量量子系统中非经典关联的总和(包括纠缠和非纠缠)。这一研究引起了人们的极大兴趣， 他们相继提出了各种度量方法，这些方法包括基于测量的度量方法［9-10］和基于相对熵的度量方法［11］以及几何量子失协［12-13］等。研究成果表明，诸如核磁共振(NMR)系统［14］、冷原子系 统［15］、光 子 系 统［16-17］、囚 禁 离 子 系 统［18］和 自 旋 系统［19-20］等都存在量子失协现象。 量子失协与量子相变［21-22］、正 定 映 射 演 化［23］和 量 子 态 广 播［24］等 紧 密 相关，在量子密码术［25］、量子态远程制备［26］和生物系统模拟［27］等方面有着广泛的应用。另外，量子失协的动力学研究结果表明，在马尔科夫环境中，量子失协比量子纠缠具有更强的抗退相干能力［16,28］。 因此，研究量子失协有助于加深对量子信息论的理解， 有助于推动量子信息技术的发展。

将固态量子系统应用于微纳加工工艺， 有利于大规模集成和扩展， 这是研发量子元器件的重要途径。 描述自旋量子间相互作用的自旋链在光晶格［29-30］、囚 禁 离 子［31-32］、超 导 量 子 比 特［33-34］和 核 磁 共振［35］等在物理系统中均有体现，自旋链模型中的量子失协也是应用物理的重要研究内容。 一维伊辛、XY 和XXZ 等自旋链系统都是可以精确求解的［36-37］，它们在研究强关联物理系统和系统临界行为方面起着重要作用。 已有的研究结果表明，利用量子失协能有效探测一维自旋链系统的量子相变点［21-22,38-40］。 在更深入的研究中，人们还考虑了外场作用［41］、三体作用［42-43］、Dzyaloshinskii-Moriya 作 用［44-46］和 热 波 动［38］等对一维自旋链系统中量子失协的影响。

一维海森堡-伊辛自旋链系统是可以精确求解的。 E. LIEB 等［36］求出了该系统的基态，找到了系统的量子相变临界点。 TAN X. D.等［47］利用量子重正化群方法研究了该系统基态中的量子纠缠， 发现量子纠缠的一阶导数在系统的量子相变点处存在发散行为。 S. KHAN 等［48］利用同样的方法研究了该系统基态中的量子失协现象， 探测到了该系统的量子相变点。以上研究主要集中在基态方面，而关于热平衡态方面的研究还比较少。在本文中，我们研究了一维海森堡-伊辛自旋链模型中的量子失协的度量及其性质， 导出了任意两自旋粒子间量子失协的解析表达式，通过数值计算结果分析了温度、海森堡-伊辛相对耦合强度和横向磁场对量子失协的影响。

1 模型与两体约化密度矩阵

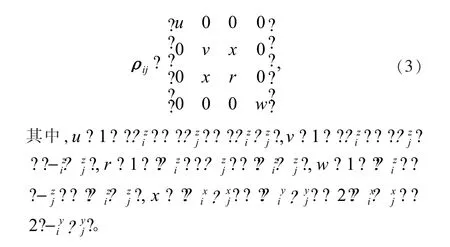
2 量子失协

该定义是由H. OLLIVIER 等最先引入的， 它被称为量子失协（Quantum Discord），其度量记为QD。

图1 不同尺 度 自旋链中 QD (− )曲线

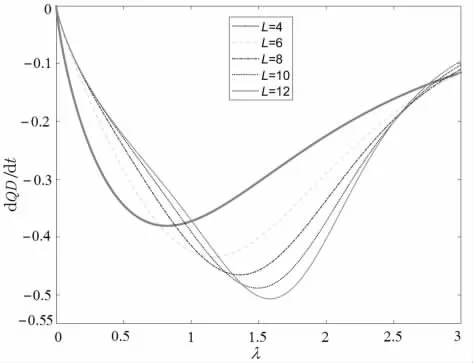
图2 不同尺度自旋链中 dQD dt曲线

图3 ln(2??) 与 ln( L)的拟合 曲 线

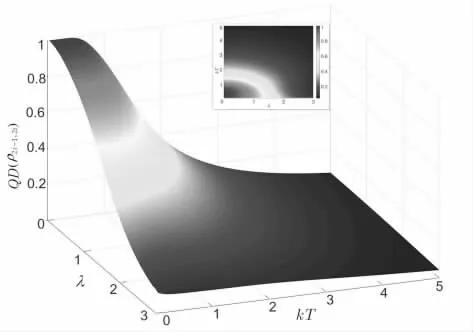
图4 h? 0时 QD (? 随 ?和 kT 的变化情况

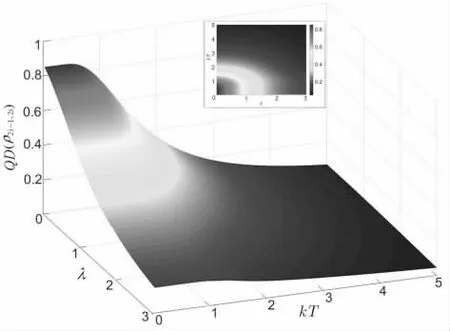
图5 h − 0.5时 QD (? 随 ?和 kT 的变化情况

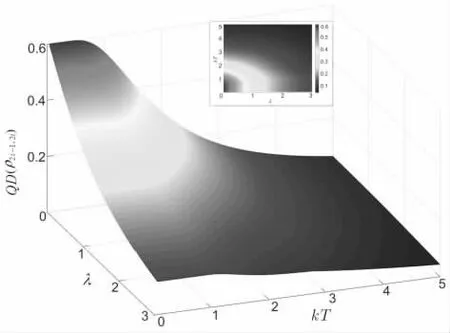
图6 h? 1时 QD (? 随 ?和 kT 的变 化 情况

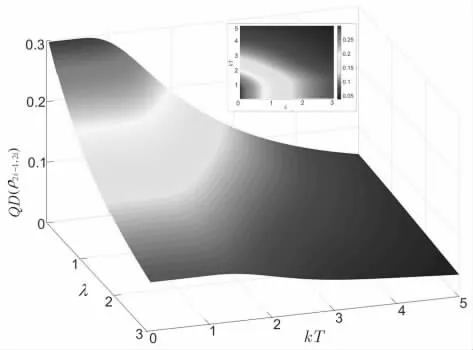
图7 h? 2时 QD (? 随 ?和 kT 的变化情况

图8、图9、图10 和图11 给出了不同温度下QD(?2i−1,2i)随耦合强度? 和 横向磁场h的变化情况。 从图8 可以看出，当kT? 0时，对于给定的h，QD(?2i−1,2i)总是随着? 的增大而减小，对于给定的小 ?，QD(?2i−1,2i)随着h 的增大而减小，当伊辛作用比较强时，QD(?2i−1,2i)不是h 的单调递减函数，在h?0附近，先随h 的增大而迅速增大，后随h 的增大而缓慢变小。 从图9 可以看出，当kT? 0.5时，QD(?2i−1,2i)的变化情况与kT?0时的类似，但其峰值有所降低，在强伊辛作用下，QD(?2i−1,2i)在h?0附近增加得比较缓慢。 从图10可以看出，当kT?2.5时，热波动对量子关联的破坏作用增强，QD(?2i−1,2i)的峰值降到0.3 以下。 从图11 可以看出，当kT? 5时，由于强热波动的影响，QD(?2i−1,2i)变化比较剧烈，这说明相应的量子失谐已被破坏。

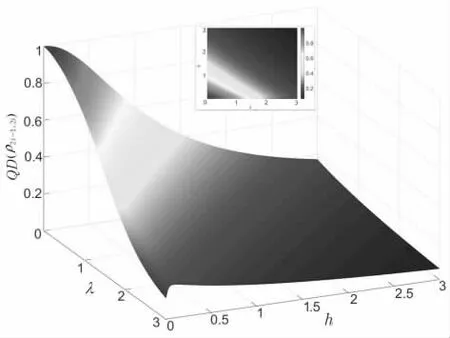
图8 kT? 0时 QD ( )随 ?和h 的变化情况

图9 kT? 1时Q D (? 随 ?和h的变化情况

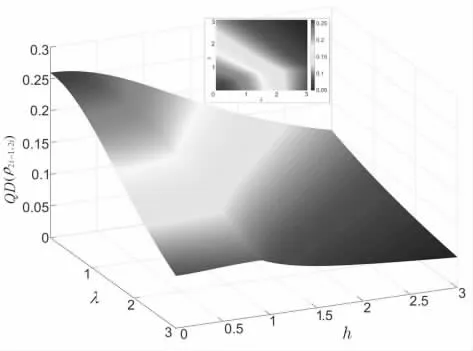
图10 kT − 2.5时 QD (? 随 ?和h 的变化情况

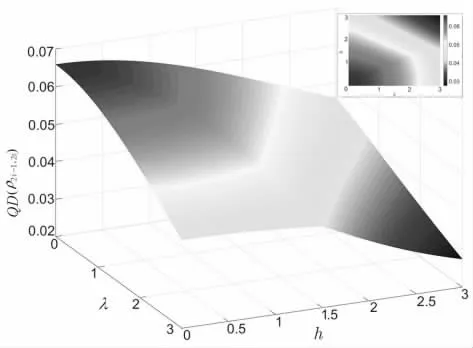
图11 kT? 5时 QD (? 随 ?和h 的变化情况

图12、图13、图14 和图15 给出了不同耦合强度 ? 下QD(?2i−1,2i)随温度kT和横向磁场h 的变化情况。 从图12 可以看出，当? ?0时，相邻两个自旋粒子间只有海森堡作用，QD(?2i−1,2i)随温度kT和横向磁场h 的增大而减小。 从图13 可以看出，当? ?1时，QD(?2i−1,2i)也有所减小， 且与 ? ?0时的情况类似。 从图14 可以看出，当 ? ?2时，在低温条件下，QD(?2i−1,2i)随h 的增大出现小范围的波动。 从图15可以看出， 当 ? ? 3时，QD(?2i−1,2i)随h 的波动行为更加明显。

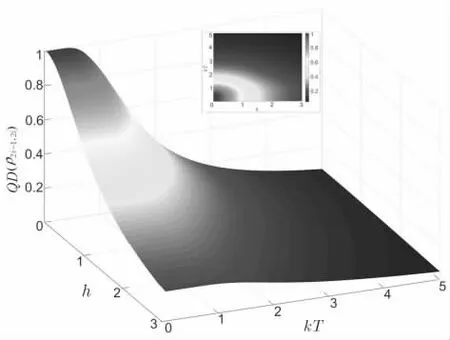
图12 ? ? 0时 QD (? )随 kT 和h 的变化情 况

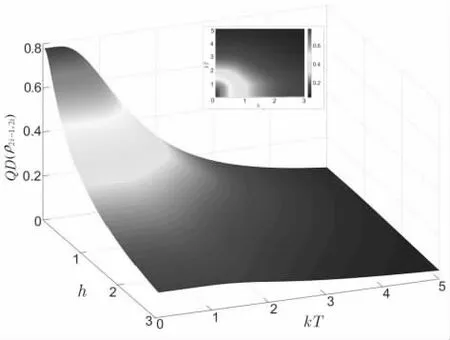
图13 ? ? 1时 QD (? )随 kT 和h 的 变化情况

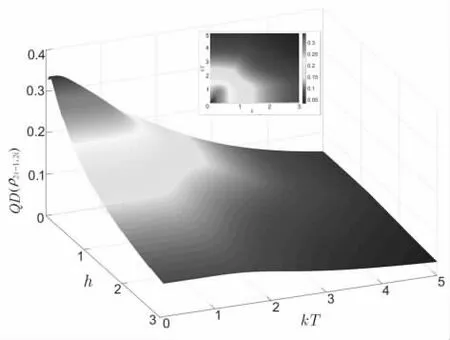
图14 ? ? 2时 QD (? )随 kT 和h 的变化情况

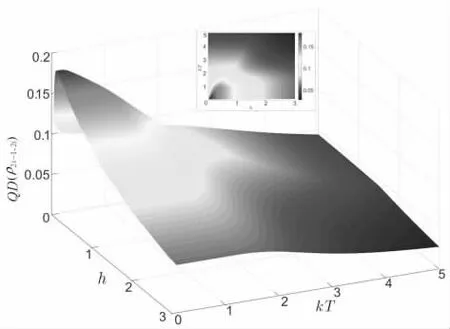
图15 ? ? 3时 QD (? 随 kT和h 的变化情况

以上结果主要是由耦合强度 ?、温度kT 和横向磁场h 相互竞争引起的。

根据以上结果，可以得出以下结论。

当温度和磁场一定时， ?取值较小时海森堡作用占据主导地位，量子整体上呈反铁磁序，量子关联较大；但随着 ?的增大，伊辛作用占据主导地位，相邻的反铁磁耦合粒子对之间的耦合作用将抑制量子的反铁磁序，削弱量子关 联，即QD(−)随 着 ?的增大而减小。

3 结束语

在本文中，我们研究了一维海森堡-伊辛自旋链模型中的两体量子失协的性质， 分析了温度、 海森堡-伊辛相对耦合强度和横向磁场对最近邻反铁磁耦合的两自旋粒子间量子失协的影响， 得出了以下结论： 在绝对零度下，QD 的一阶导数的极小值点在系统的量子相变点附近存在标度行为； 随着温度升高和耦合强度增大，QD 不断变小； 当伊辛作用足够强和温度比较低的条件下，QD 在横向磁场中将表现出明显的波动行为。